Schema Refinement Normal Forms Normal Forms n n

Schema Refinement: Normal Forms

Normal Forms n n Given <R, F>, a relation schema R together with a set of FD’s, we want to determine if R is in a “good” shape! If not, we need to decompose R into smaller “good” relations; How to measure this goodness and how to achieve it? To address these issues, we need to study normal forms If a relation schema is in some normal form, we

Normal Forms n The normal forms based on FD’s are n n n First normal form (1 NF) Second normal form (2 NF) Third normal form (3 NF) Boyce-Codd normal form (BCNF) These normal forms have increasingly restrictive requirements BCNF 3 NF 2 NF 1 NF

First & Second Normal Forms A relation scheme is said to be in first normal from (1 NF) if the values in the domain of each attribute of the relation are atomic. In other words, only one value is associated with each attribute and the value is not a set of values or a list of values. A database scheme is in first normal form if every relation scheme included in the database scheme is in 1 NF. A relation scheme R<S, F> is in second normal from (2 NF) if it is in the 1 NF and if all nonprime attributes are fully functionally dependent on the relation key(s). A database scheme is in second normal form if every relation scheme included in

Third Normal Form Let R be a relation schema, F a set of FD’s on R, X ⊆ R, and A ∈ R. n We say R w. r. t. F is in third normal form (3 NF), if for each FD X A in F, at least one of the following conditions holds: n A X (that is, X A is a trivial FD), or n X is a superkey, or n If X is not a key, then A is part of some key of R n To determine whether <R, F> is in 3 NF: n For every non-trivial FD X A in F, we check whether X is a superkey. If not, we then check whether its RHS, A, is part of any key of R. If both conditions fail, we

Boyce-Codd Normal Form Let R be a relation schema, F a set of FD’s on R, X ⊆ R, and A ∈ R. n We say R w. r. t. F is in Boyce-Codd normal form (BCNF), if for each FD X A in F, at least one of the following holds: n A X (that is the FD is trivial) or n X is a superkey n To determine whether <R, F> is in BCNF or not, we check every non-trivial FD in F. n If there exists a FD X A in F such that X+ ≠ R, then

Decomposition into BCNF n Consider <R, F>, where R is in 1 NF. n If R is not in BCNF, we can always obtain a lossless-join decomposition of R into a collection of BCNF relations n However, it may not always be dependency preserving n The basic step of a BCNF algorithm: Suppose X A F is a FD violating the BCNF requirement, where X R and A R n Decompose R into XA and R – A n If either R – A or XA is not in BCNF, decompose it further

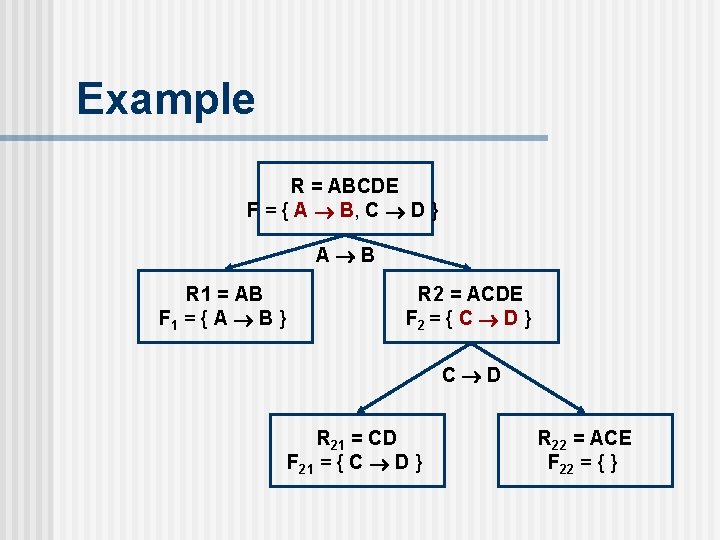
Example R = ABCDE F = { A B, C D } A B R 1 = AB F 1 = { A B } R 2 = ACDE F 2 = { C D } C D R 21 = CD F 21 = { C D } R 22 = ACE F 22 = { }

Decomposition into 3 NF n We can always obtain a lossless-join, dependencypreserving decomposition of a relation into 3 NF relations. How? n We discuss 2 approaches to decompose <R, F>. n First: Approach 1: Follow the binary decomposition method for BCNF Let R = { R 1, R 2, . . . Rn} be the result. Recall that this is always lossless-join, but may not preserve the FD’s; so need to fix it? n n n Identify the set N of FD’s in F that are lost (i. e. , not preserved) For each FD X A in N, create a relation schema XA and add it to R A refinement step: if there are several FD’s with the same LHS,

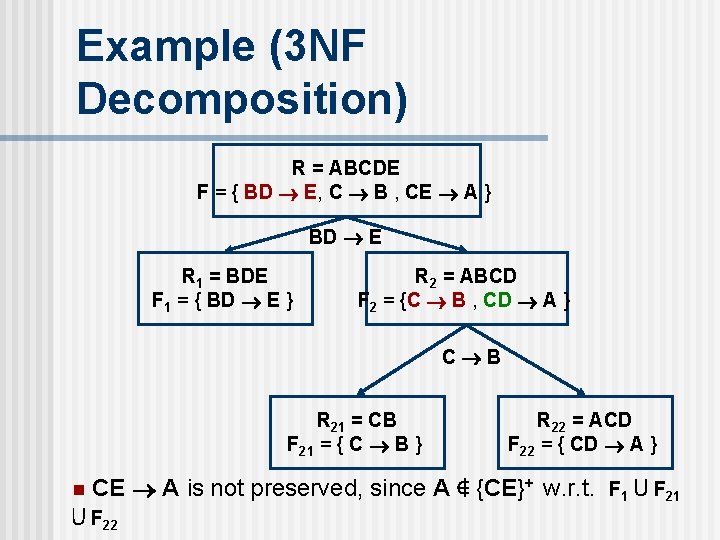
Example (3 NF Decomposition) R = ABCDE F = { BD E, C B , CE A } BD E R 1 = BDE F 1 = { BD E } R 2 = ABCD F 2 = {C B , CD A } C B R 21 = CB F 21 = { C B } n R 22 = ACD F 22 = { CD A } CE A is not preserved, since A ∉ {CE}+ w. r. t. F 1 ⋃ F 22

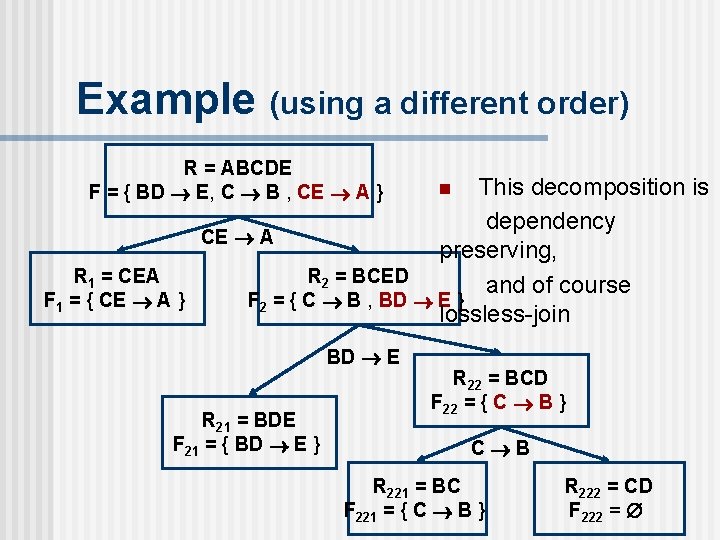
Example (using a different order) R = ABCDE F = { BD E, C B , CE A } This decomposition is dependency CE A preserving, R 1 = CEA R 2 = BCED and of course F 1 = { CE A } F 2 = { C B , BD E } lossless-join BD E R 21 = BDE F 21 = { BD E } n R 22 = BCD F 22 = { C B } C B R 221 = BC F 221 = { C B } R 222 = CD F 222 =

Decomposition into 3 NF n Previous (binary decomposition approach): Lossless-join √ n May not be dependency preserving. If so, then add extra relations XA, one for each FD X → A we lost n n Now, the synthesis approach Dependency preservation √ n However, may not be lossless-join. If so, we need to add to R, only one extra relation schema that includes the attributes that form n

Decomposition into 3 NF (synthesis) Consider relation schema <R, F> n The synthesis approach: Get a canonical cover Fc of F n For each FD X A in Fc, add schema XA to R n If the decomposition R is not lossless, need to fix it. Add to R an extra relation schema containing just those attributes that form any key of R n

Example n n n R = ( A, B, C ) F = { A B, C B } Decompose R into R 1 = ( A, B ) and R 2 = ( B, C ) This decomposition is not lossless Add R 3 = ( A, C ) The decomposition R = {R 1, R 2, R 3} is both lossless and dependencypreserving

Ann Algorithm to Check Lossless join Suppose relation R{A 1 , . . . , Ak} is decomposed into R 1, . . . , Rn To determine if this decomposition is lossless, we use a table, L[ 1 … n ] [ 1. . . k ] Initializing the table: for each relation Ri do for each attribute Aj do if Aj is an attribute in Ri then L [ i ][ j ] a. Aj else L [ i ][ j ] bi. Aj

Algorithm to Check Lossless (cont’d) repeat for each FD X Y in F do: if ∃ rows i and j such that L [ i ] == L [ j ], for each attribute in X, then for ∀ column t corresponding to an attribute At in Y do: if L [ i ][ t ] == a. At then L [ j ][ t ] a. At else if L [ j ][ t ] == a. At then L [ i ][ t ] a. At else L [ j ][ t ] L [ i ][ t ] until no change The decomposition is lossless if, after performing this algorithm, L contains a row of all a’s. That is, if there exists a row i in L such that: L [ i ][ t

Examples n n Given ≺R, F≻, where R = ( A, B, C, D ), and F = { A B, A C, C D } is a set of FD’s on R Is the decomposition R = {R 1, R 2} lossless, where R 1 = ( A, B, C ) and R 2 = ( C , D)? n n n To be discussed in class Now consider S = ( A, B, C, D, E ) and the set G of FD’s on S, where G = { AB CD, A E, C D } Is decomposition of S = {S 1, S 2, S 3} lossless, where

Dependency-Preserving Checking n n Let ≺R, F≻, where F = {X 1 Y 1, …, Xn Yn}. Let R ={ R 1, …, Rk } be a decomposition of R and Fi be the projection of F on Ri Below is an algorithm that decides dependency preservation. preserved TRUE for each FD X Y in F and while preserved == TRUE do begin compute X+ under F 1 . . . Fn ;

Example Consider R = ( A, B, C, D ), F = { A B, B C, C D } Is the decomposition R = {R 1, R 2} dependency-preserving, where n n R 1 = ( A, B ), F 1 = { A B }, R 2 = ( A, C , D), and F 2 = { C D, A C }? n Check if A B is preserved • • n Compute A+ under { A B } { C D, A C } • A+ = { A, B, D } • Yes Check if B A+ • A B is preserved • Compute B+ under { A B } { C D, A C } Check if B C is preserved • • • B+ = { B } • No Check if C B+ B C is not preserved