Multiwinner Voting Theory Experiments and Data Piotr Faliszewski




















![Committee Scoring Rules β- > > > > [FSST 16] P. Faliszewski, P. Skowron, Committee Scoring Rules β- > > > > [FSST 16] P. Faliszewski, P. Skowron,](https://slidetodoc.com/presentation_image/5b478abf0b0c814ddc0fcc4dc05cbc58/image-46.jpg)
![Committee Scoring Rules β- > > > > [FSST 16] P. Faliszewski, P. Skowron, Committee Scoring Rules β- > > > > [FSST 16] P. Faliszewski, P. Skowron,](https://slidetodoc.com/presentation_image/5b478abf0b0c814ddc0fcc4dc05cbc58/image-47.jpg)
![Committee Scoring Rules Committee SNT monotone V noncrossing monotone Bloc ble [FSST 16] P. Committee Scoring Rules Committee SNT monotone V noncrossing monotone Bloc ble [FSST 16] P.](https://slidetodoc.com/presentation_image/5b478abf0b0c814ddc0fcc4dc05cbc58/image-49.jpg)



![Axioms for Diversity: Narrow Top [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Axioms for Diversity: Narrow Top [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N.](https://slidetodoc.com/presentation_image/5b478abf0b0c814ddc0fcc4dc05cbc58/image-54.jpg)

![Axioms: Narrow Top + Top Member Monotonicity [FSST 16] P. Faliszewski, P. Skowron, A. Axioms: Narrow Top + Top Member Monotonicity [FSST 16] P. Faliszewski, P. Skowron, A.](https://slidetodoc.com/presentation_image/5b478abf0b0c814ddc0fcc4dc05cbc58/image-63.jpg)







- Slides: 80

Multiwinner Voting: Theory, Experiments and Data Piotr Faliszewski AGH University of Science and Technology Kraków, Poland faliszew@agh. edu. pl Based on joint works with Edith Elkind (University of Oxford, UK), Jerome Lang (Dauphine Paris, FR), Jean-Francois Laslier (Paris School of Economics, FR), Piotr Skowron (Technische Universtaet Berlin, DE), Arkadii Slinko (University of Auckland, NZ), Nimrod Talmon (Weizmann Institute, IL)

Multiwinner Voting: Theory, Experiments and Data and Theory! Piotr Faliszewski AGH University of Science and Technology Kraków, Poland faliszew@agh. edu. pl Based on joint works with Edith Elkind (University of Oxford, UK), Jerome Lang (Dauphine Paris, FR), Jean-Francois Laslier (Paris School of Economics, FR), Piotr Skowron (Technische Universtaet Berlin, DE), Arkadii Slinko (University of Auckland, NZ), Nimrod Talmon (Weizmann Institute, IL)

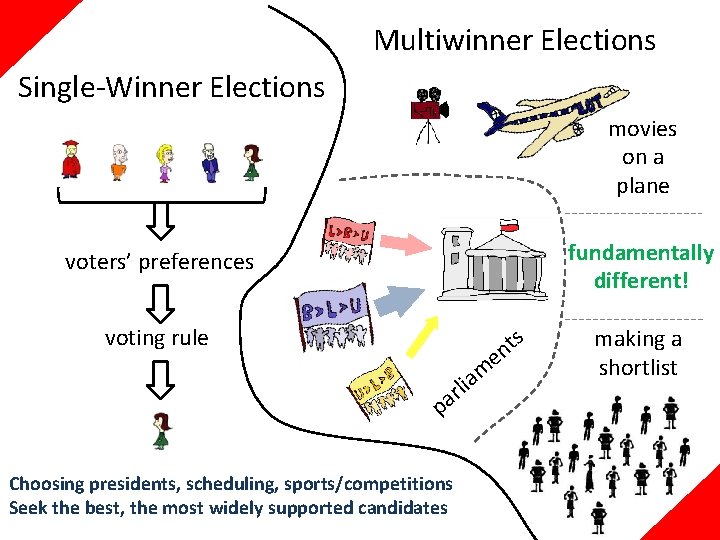
Multiwinner Elections Single-Winner Elections movies on a plane fundamentally different! voters’ preferences voting rule t n e m a i rl pa Choosing presidents, scheduling, sports/competitions Seek the best, the most widely supported candidates s making a shortlist

Single-Winner Scoring Rules A single-winner scoring function: f(i) = score for position i The candidate with the highest sum of scores is the winner C={ , , , V = (v 1, … , v 6) 4 V 1: Examples: V 2: Borda score β(i) = m-i V 3: V 4: V 5: V 6: 3 2 , 1 0 }

Single-Winner Scoring Rules A single-winner scoring function: f(i) = score for position i The candidate with the highest sum of scores is the winner C={ , , , V = (v 1, … , v 6) 1 V 1: Examples: V 2: Borda score β(i) = m-i V 3: t-Approval score αt(i) = 1 if i ≤ t and 0 otherwise V 4: V 5: V 6: 1 0 , 0 0 }

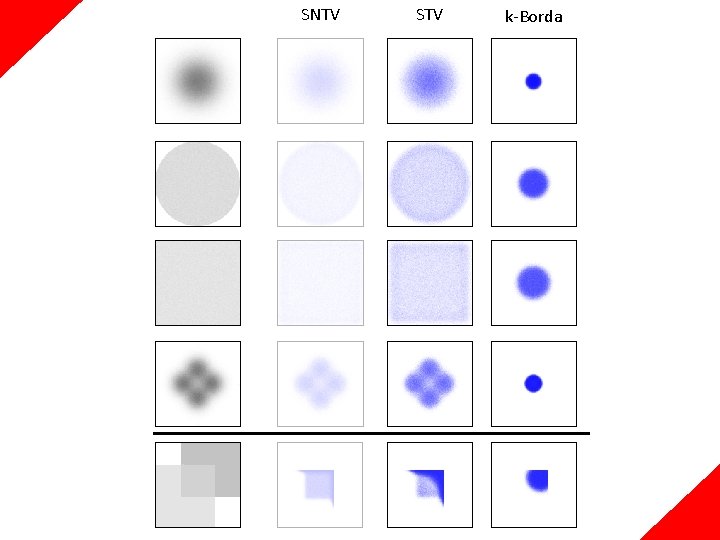
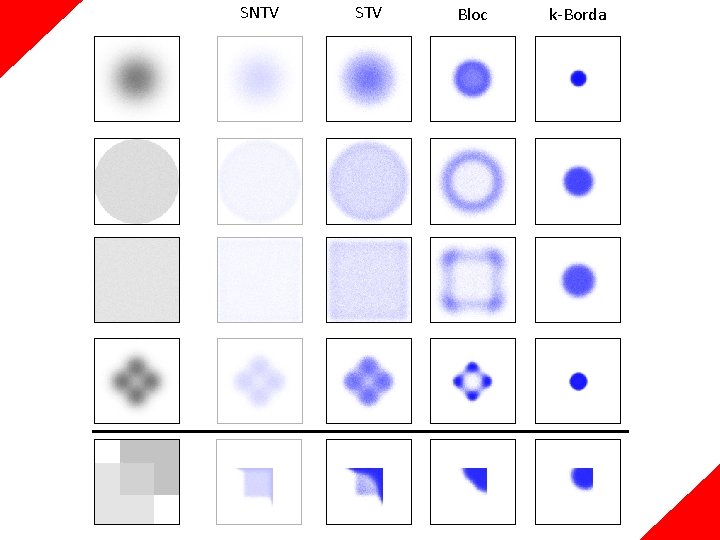
Committee Elections: Examples SNTV: Pick k candidates with top plurality scores (α 1) C={ , , , V = (v 1, … , v 6) 1 V 1: V 2: V 3: V 4: V 5: V 6: 0 0 , 0 0 }

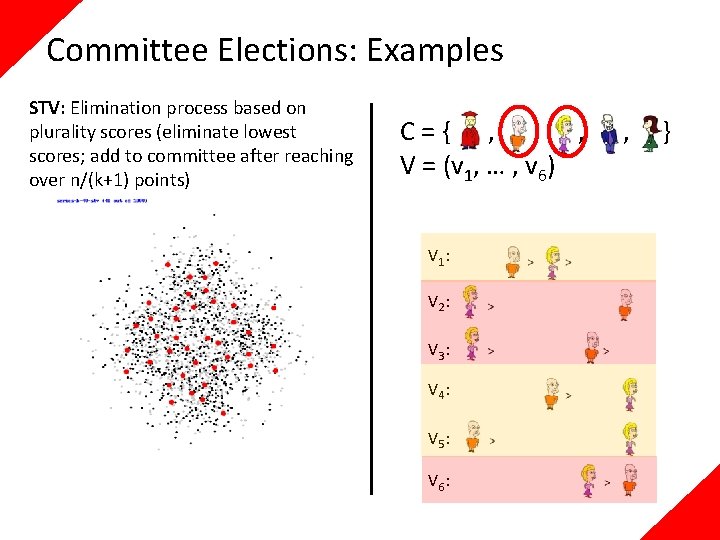
Committee Elections: Examples STV: Elimination process based on plurality scores (eliminate lowest scores; add to committee after reaching over n/(k+1) points) C={ , , , V = (v 1, … , v 6) V 1: V 2: V 3: V 4: V 5: V 6: , }

Committee Elections: Examples k-Borda: Pick k candidates with top Borda scores (β) C={ , , , V = (v 1, … , v 6) 4 V 1: V 2: V 3: V 4: V 5: V 6: 3 2 , 1 0 }

SNTV STV k-Borda

Generating the Histograms AGH Comp. Sci. Dept. (8 -core subcluster) Easy rules (P-time) (k-Borda, SNTV, …) 10 000 elections x rules x distributions Store and never look at them again (1 -3 TB) Aggregate results 10 000 elections x rules x distributions Weizmann Institute (heavy-duty cluster) NP-hard rules (CPLEX ILP-based alg. )

Generating the Histograms AGH Comp. Sci. Dept. (8 -core subcluster) Easy rules (P-time) (k-Borda, SNTV, …) 10 000 elections x rules x distributions Store and never look at them again (1 -3 TB) Aggregate results 10 000 elections x rules x distributions Weizmann Institute (heavy-duty cluster) NP-hard rules (CPLEX ILP-based alg. )

We Want to Understand Committee Rules

Committee Scoring Rules Consider a preference order: a committee Position of the committee = (1, 3, 4 ) f(i 1, i 2, …, ik) = the score of the committee Assuming i 1 < i 2 < … < ik [EFSS 17] E. Elkind, P. Faliszewski, P. Skowron, A. Slinko, Properties of Multiwinner Voting Rules, Social Choice and Welfare, 2017 [SFS 16] P. Skowron, P. Faliszewski, A. Slinko, Axiomatic Characterization of Committee Scoring Rules, ar. Xiv 2016

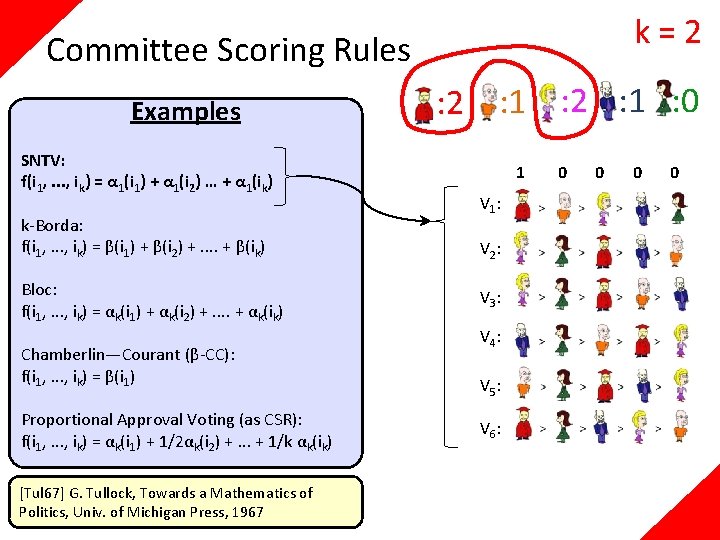
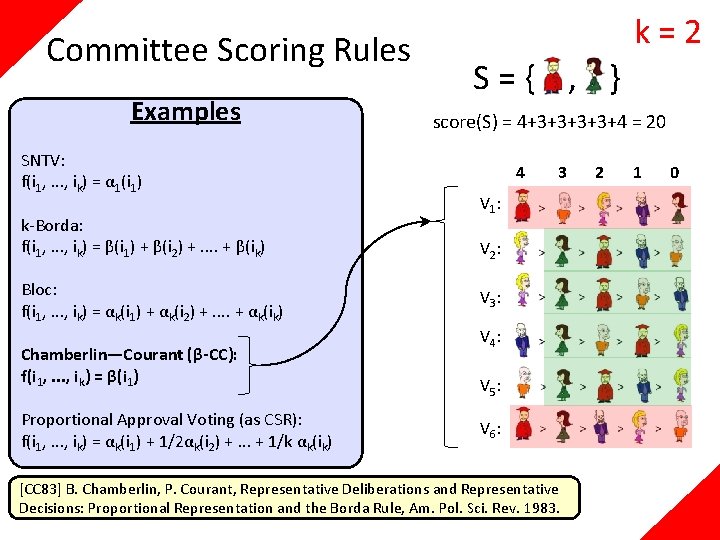
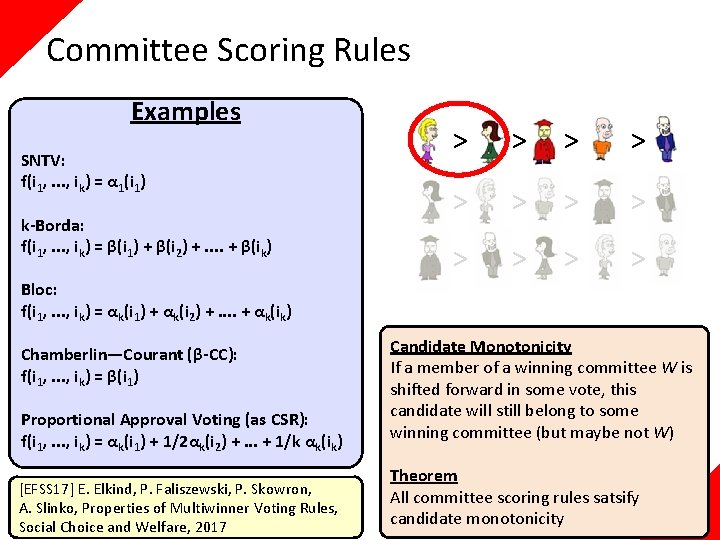
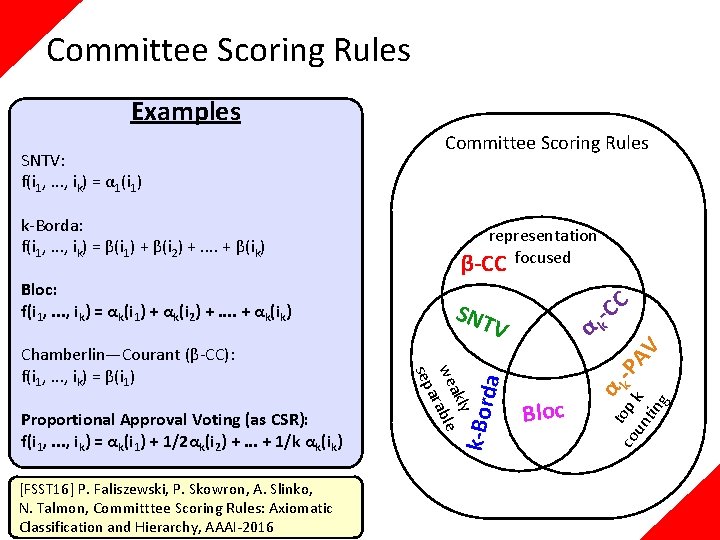
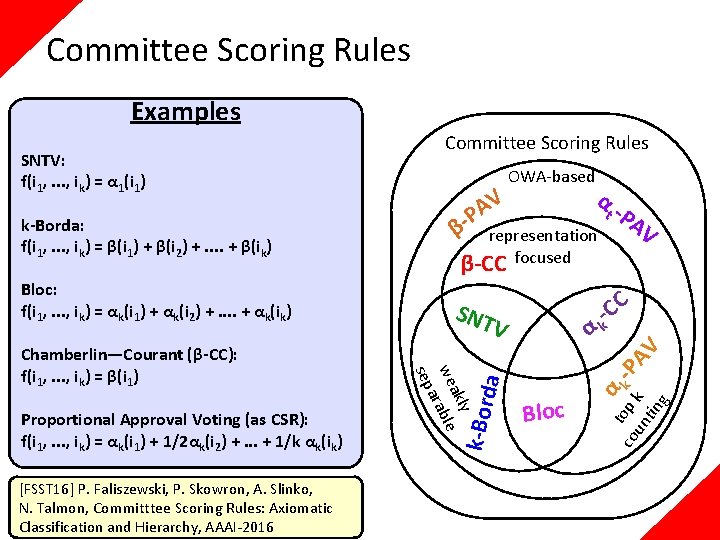
Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) + α 1(i 2) … + α 1(ik) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik)

k=2 Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) + α 1(i 2) … + α 1(ik) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [Tul 67] G. Tullock, Towards a Mathematics of Politics, Univ. of Michigan Press, 1967 : 2 : 1 : 0 1 V 1: V 2: V 3: V 4: V 5: V 6: 0 0

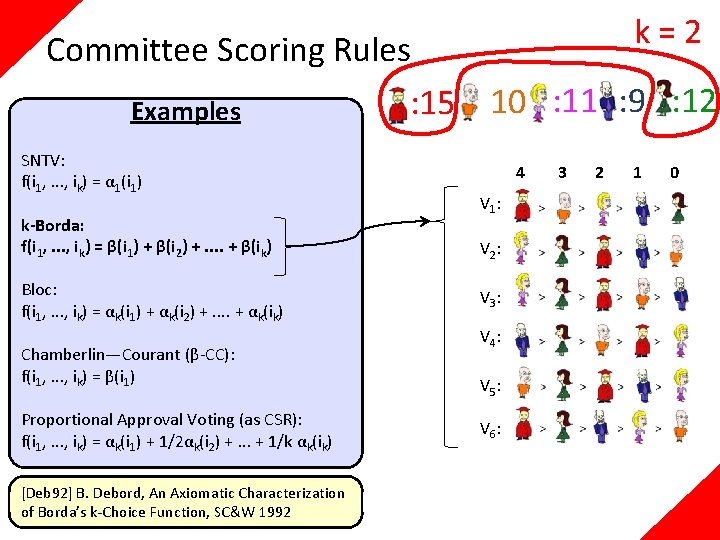
k=2 Committee Scoring Rules : 15 : 10 : 11 : 9 : 12 Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [Deb 92] B. Debord, An Axiomatic Characterization of Borda’s k-Choice Function, SC&W 1992 4 V 1: V 2: V 3: V 4: V 5: V 6: 3 2 1 0

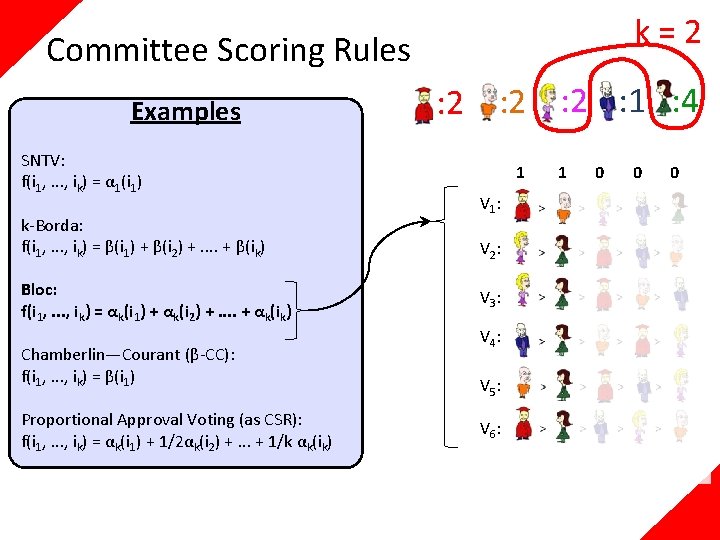
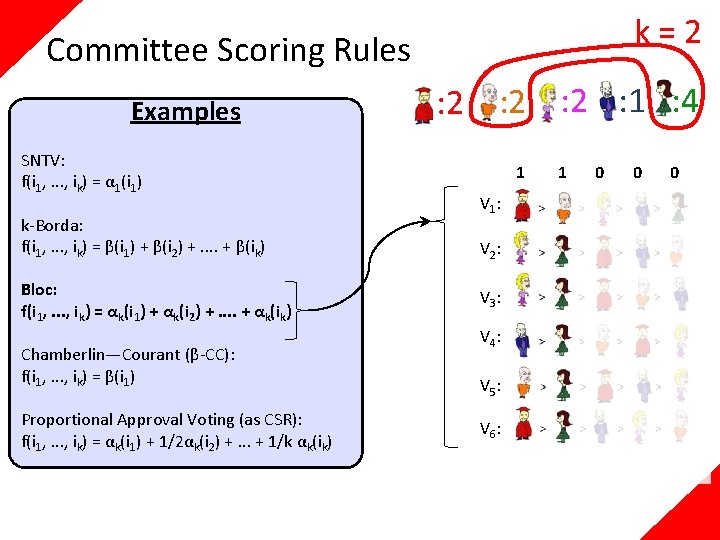
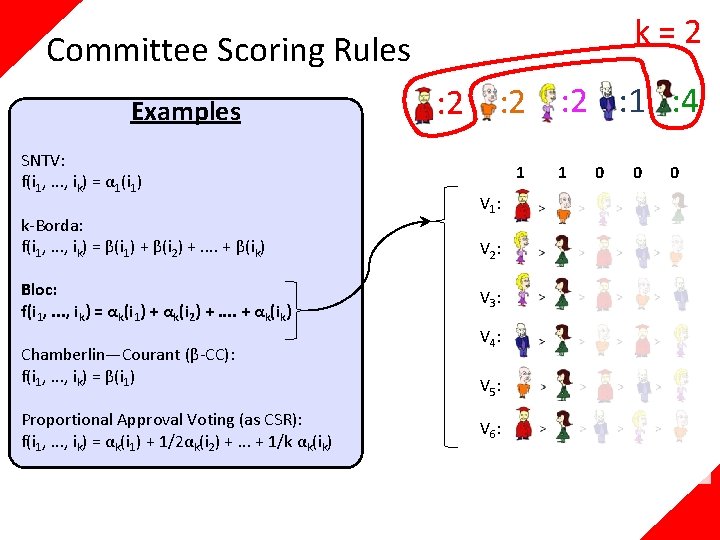
k=2 Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) : 2 : 2 : 1 : 4 1 V 1: V 2: V 3: V 4: V 5: V 6: 1 0 0 0

k=2 Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) : 2 : 2 : 1 : 4 1 V 1: V 2: V 3: V 4: V 5: V 6: 1 0 0 0

k=2 Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) : 2 : 2 : 1 : 4 1 V 1: V 2: V 3: V 4: V 5: V 6: 1 0 0 0

Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik)

SNTV STV Bloc k-Borda

Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) k=2 S={ , } score(S) = 4+3+3+4 = 20 4 3 V 1: V 2: V 3: V 4: V 5: V 6: [CC 83] B. Chamberlin, P. Courant, Representative Deliberations and Representative Decisions: Proportional Representation and the Borda Rule, Am. Pol. Sci. Rev. 1983. 2 1 0

Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [CC 83] B. Chamberlin, P. Courant, Representative Deliberations and Representative Decisions: Proportional Representation and the Borda Rule, Am. Pol. Sci. Rev. 1983.

Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [CC 83] B. Chamberlin, P. Courant, Representative Deliberations and Representative Decisions: Proportional Representation and the Borda Rule, Am. Pol. Sci. Rev. 1983.

SNTV STV CC Bloc k-Borda

k=3 Committee Scoring Rules Examples 1 1 1 0 0 SNTV: f(i 1, . . . , ik) = α 1(i 1) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) score({ , , }) = 1∙ 1 + 1/2∙ 1 + 1/3∙ 0 = 3/2 Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [Thi 95] N. Thiele, Om Flerfoldsvalg, Oversigt over det Kongelige Danske Videnskabernes Selskabs Forhandlinger, 1895 [Kil 10] M. Kilgour, Approval Balloting for Multi-Winner Elections, Hanbook of Approval Voting 2010

Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [EFSS 17] E. Elkind, P. Faliszewski, P. Skowron, A. Slinko, Properties of Multiwinner Voting Rules, Social Choice and Welfare, 2017 Consistency If W is a winning committee under two elections, E 1 and E 2, then W is a winning committee under E 1+E 2 (and only such committees win in E 1+E 2)

Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [EFSS 17] E. Elkind, P. Faliszewski, P. Skowron, A. Slinko, Properties of Multiwinner Voting Rules, Social Choice and Welfare, 2017 Consistency If W is a winning committee under two elections, E 1 and E 2, then W is a winning committee under E 1+E 2 (and only such committees win in E 1+E 2)

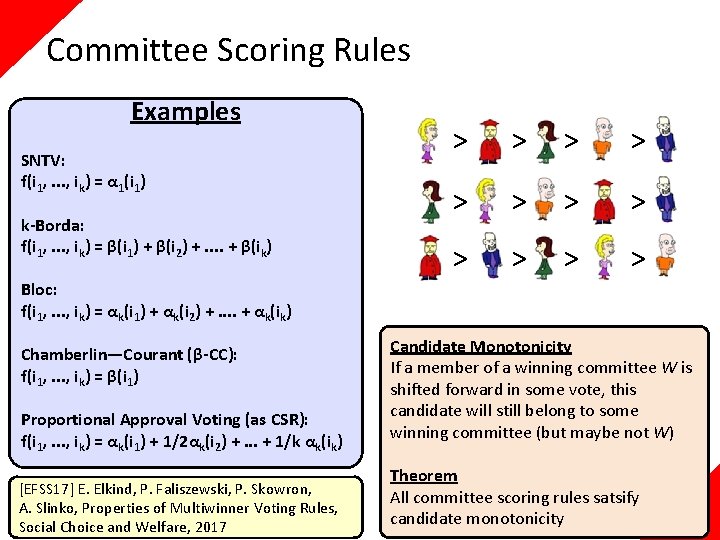
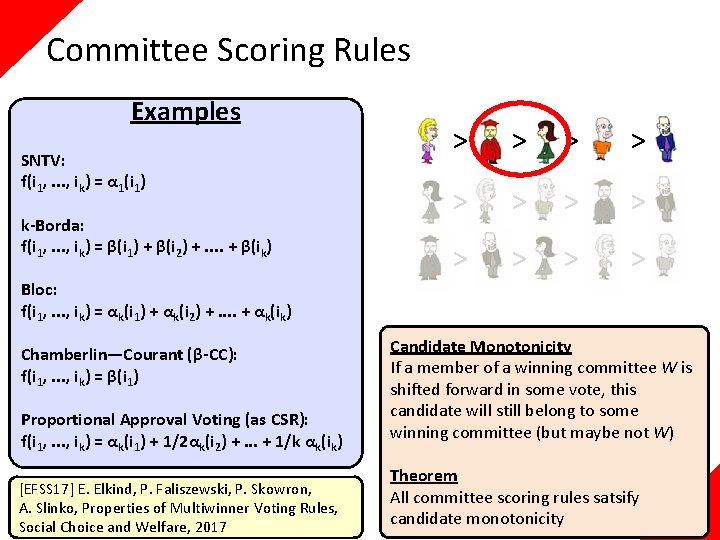
Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [EFSS 17] E. Elkind, P. Faliszewski, P. Skowron, A. Slinko, Properties of Multiwinner Voting Rules, Social Choice and Welfare, 2017 Consistency If W is a winning committee under two elections, E 1 and E 2, then W is a winning committee under E 1+E 2 (and only such committees win in E 1+E 2) Theorem All committee scoring rules satisfy consistency Candidate Monotonicity If a member of a winning committee W is shifted forward in some vote, this candidate will still belong to some winning committee (but maybe not W) Theorem All committee scoring rules satsify candidate monotonicity

Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) > > > Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [EFSS 17] E. Elkind, P. Faliszewski, P. Skowron, A. Slinko, Properties of Multiwinner Voting Rules, Social Choice and Welfare, 2017 Candidate Monotonicity If a member of a winning committee W is shifted forward in some vote, this candidate will still belong to some winning committee (but maybe not W) Theorem All committee scoring rules satsify candidate monotonicity

Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) > > > Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [EFSS 17] E. Elkind, P. Faliszewski, P. Skowron, A. Slinko, Properties of Multiwinner Voting Rules, Social Choice and Welfare, 2017 Candidate Monotonicity If a member of a winning committee W is shifted forward in some vote, this candidate will still belong to some winning committee (but maybe not W) Theorem All committee scoring rules satsify candidate monotonicity

Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) > > > Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [EFSS 17] E. Elkind, P. Faliszewski, P. Skowron, A. Slinko, Properties of Multiwinner Voting Rules, Social Choice and Welfare, 2017 Candidate Monotonicity If a member of a winning committee W is shifted forward in some vote, this candidate will still belong to some winning committee (but maybe not W) Theorem All committee scoring rules satsify candidate monotonicity

Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 Committee Scoring Rules

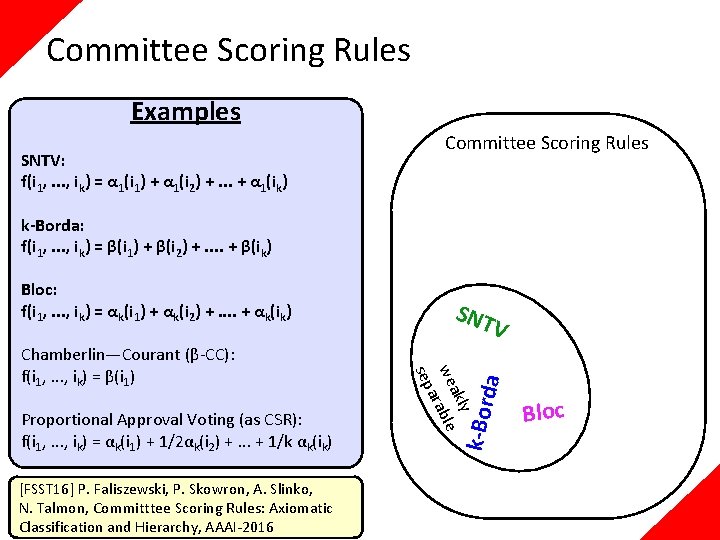
Committee Scoring Rules Examples SNTV: f(i 1, . . . , ik) = α 1(i 1) + α 1(i 2) +. . . + α 1(ik) Committee Scoring Rules k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 V da y akl we rable a sep Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) SNT k-Bor Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Bloc

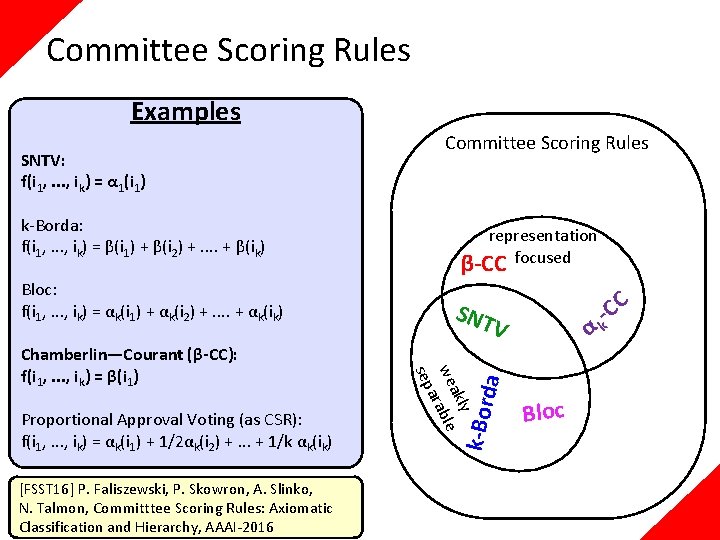
Committee Scoring Rules Examples Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 SNT V y akl we rable a sep Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) representation β-CC focused da k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) k-Bor SNTV: f(i 1, . . . , ik) = α 1(i 1) Committee Scoring Rules α Bloc C -C k

Committee Scoring Rules Examples Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 V y akl we rable a sep Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) SNT α Bloc C -C k α t o co p k -P un k AV tin g Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) representation β-CC focused da k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) k-Bor SNTV: f(i 1, . . . , ik) = α 1(i 1) Committee Scoring Rules

Committee Scoring Rules Examples Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 α representation β-CC focused SNT V y akl we rable a sep Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) OWA-based α Bloc t -P AV C -C k α t o co p k -P un k AV tin g Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) β- da k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) V A P k-Bor SNTV: f(i 1, . . . , ik) = α 1(i 1) Committee Scoring Rules

Committee Scoring Rules Examples Proportional Approval Voting (as CSR): f(i 1, . . . , ik) = αk(i 1) + 1/2αk(i 2) +. . . + 1/k αk(ik) [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 α representation β-CC focused SNT V y akl we rable a sep Chamberlin—Courant (β-CC): f(i 1, . . . , ik) = β(i 1) OWA-based α Bloc t -P AV C -C k α t o co p k -P un k AV tin g Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) β- da k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) V A P k-Bor SNTV: f(i 1, . . . , ik) = α 1(i 1) Committee Scoring Rules

Nature of the Committees (Individual Excellence)

Excellence: Main Idea Given: A group of candidates and preferences of the judges/voters Task: Select k best candidates (the finalists)

Excellence: Main Idea Given: A group of candidates and preferences of the judges/voters Task: Select k best candidates (the finalists)

Excellence: Main Idea Committee Selection Given: A group of candidates and preferences of the judges/voters Task: Select k best candidates (the finalists) Final Selection Later: Select the overall winner

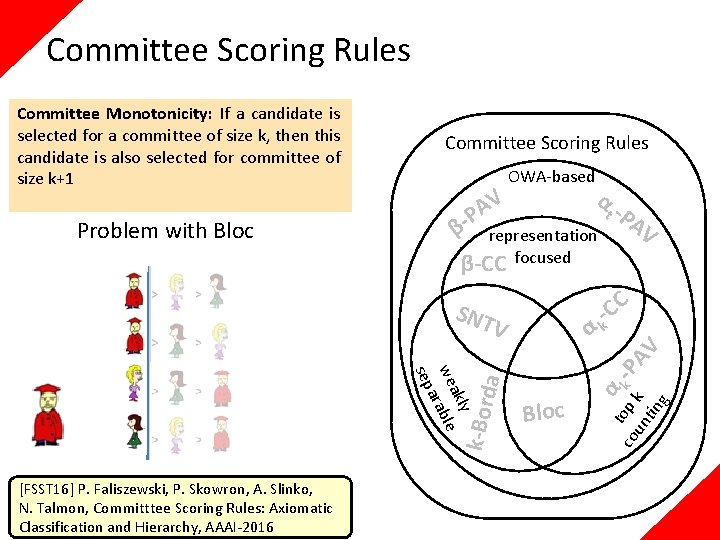
Committee Scoring Rules Problem with Bloc Committee Scoring Rules β- V A P OWA-based representation β-CC focused SNT V k-Bor da y akl we rable a sep [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 α α Bloc t -P AV C -C k α t o co p k -P un k AV tin g Committee Monotonicity: If a candidate is selected for a committee of size k, then this candidate is also selected for committee of size k+1

Committee Scoring Rules Problem with Bloc Committee Scoring Rules β- V A P OWA-based representation β-CC focused SNT V k-Bor da y akl we rable a sep [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 α α Bloc t -P AV C -C k α t o co p k -P un k AV tin g Committee Monotonicity: If a candidate is selected for a committee of size k, then this candidate is also selected for committee of size k+1

Committee Scoring Rules β- α α le Bloc t -P AV C -C k α t o co p k -P un k AV tin g da rab [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 SNT committee V monotone a sep SNTV: f(i 1, . . . , ik) = α 1(i 1) + α 1(i 2) +. . . + α 1(ik) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) OWA-based representation β-CC focused Theorem A committee scoring rule is committee monotone if and only if it is separable. Separable Rules V A P k-Bor Committee Monotonicity: If a candidate is selected for a committee of size k, then this candidate is also selected for committee of size k+1
![Committee Scoring Rules β FSST 16 P Faliszewski P Skowron Committee Scoring Rules β- > > > > [FSST 16] P. Faliszewski, P. Skowron,](https://slidetodoc.com/presentation_image/5b478abf0b0c814ddc0fcc4dc05cbc58/image-46.jpg)
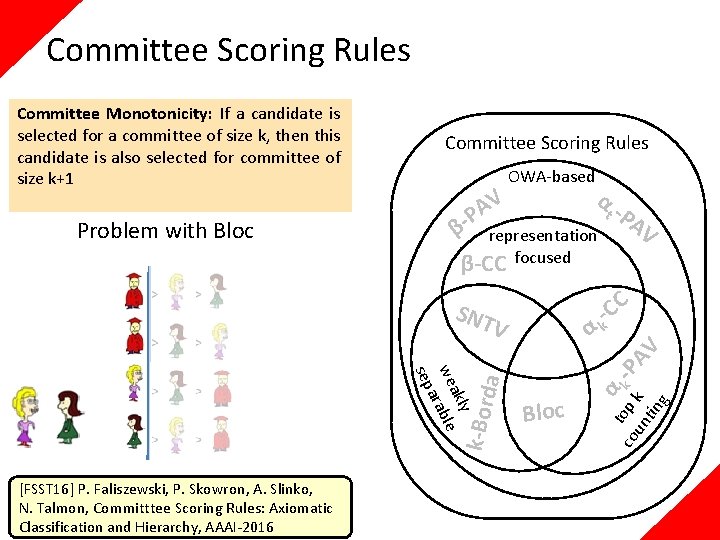
Committee Scoring Rules β- > > > > [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 le > rab > a sep > SNT committee V monotone da > α representation β-CC focused k-Bor > V A P OWA-based α Bloc t -P AV C -C k α t o co p k -P un k AV tin g Noncrossing Monotonicity: If a member of the winning committee is moved forward (without passing another committee member), the committee is still winning
![Committee Scoring Rules β FSST 16 P Faliszewski P Skowron Committee Scoring Rules β- > > > > [FSST 16] P. Faliszewski, P. Skowron,](https://slidetodoc.com/presentation_image/5b478abf0b0c814ddc0fcc4dc05cbc58/image-47.jpg)
Committee Scoring Rules β- > > > > [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 le > rab > a sep > SNT committee V monotone da > α representation β-CC focused k-Bor > V A P OWA-based α Bloc t -P AV C -C k α t o co p k -P un k AV tin g Noncrossing Monotonicity: If a member of the winning committee is moved forward (without passing another committee member), the committee is still winning

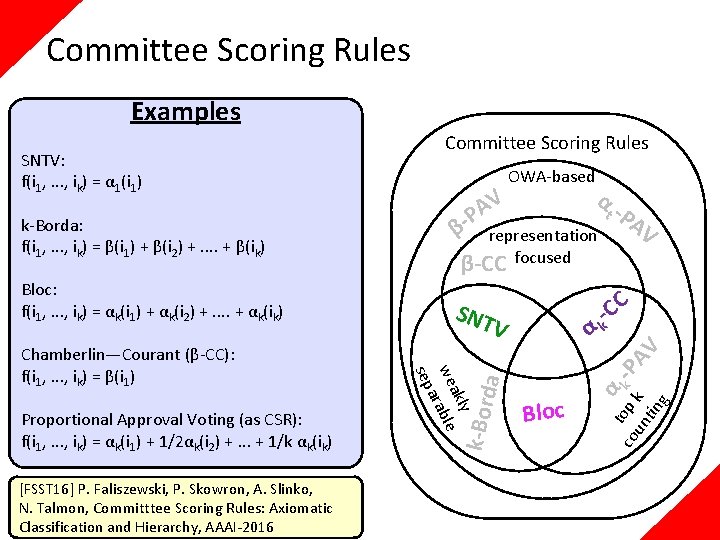
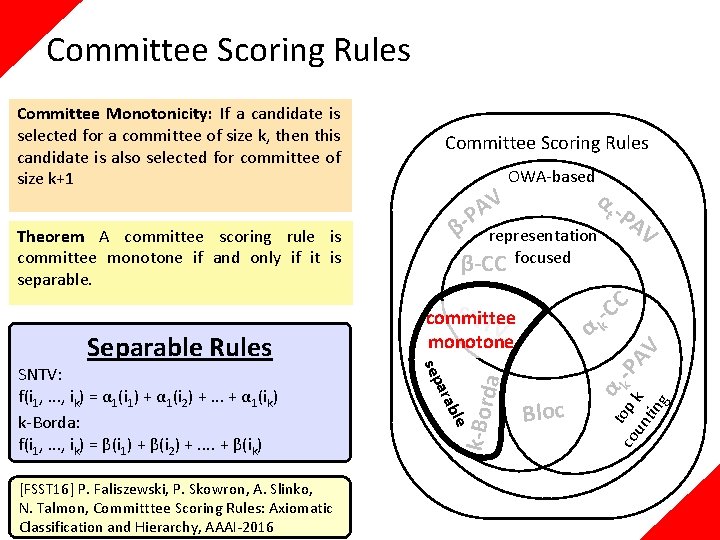
Committee Scoring Rules Theorem A committee scoring rule is noncrossing monotone if and only if it is weakly separable. α α le Bloc t -P AV C -C k α t o co p k -P un k AV tin g rab [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 SNT committee V monotone a sep SNTV: f(i 1, . . . , ik) = α 1(i 1) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) OWA-based representation β-CC focused da Weakly Separable Rules β- V A P k-Bor Noncrossing Monotonicity: If a member of the winning committee is moved forward (without passing another committee member), the committee is still winning
![Committee Scoring Rules Committee SNT monotone V noncrossing monotone Bloc ble FSST 16 P Committee Scoring Rules Committee SNT monotone V noncrossing monotone Bloc ble [FSST 16] P.](https://slidetodoc.com/presentation_image/5b478abf0b0c814ddc0fcc4dc05cbc58/image-49.jpg)
Committee Scoring Rules Committee SNT monotone V noncrossing monotone Bloc ble [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 representation β-CC focused ara sep SNTV: f(i 1, . . . , ik) = α 1(i 1) Bloc: f(i 1, . . . , ik) = αk(i 1) + αk(i 2) +. . + αk(ik) k-Borda: f(i 1, . . . , ik) = β(i 1) + β(i 2) +. . + β(ik) α Weakly separable α t -P AV C -C k α t o co p k -P un k AV tin g Weakly Separable Rules β- V A P OWA-based da Theorem A committee scoring rule is noncrossing monotone if and only if it is weakly separable. Committee Scoring Rules k-Bor Noncrossing Monotonicity: If a member of the winning committee is moved forward (without passing another committee member), the committee is still winning

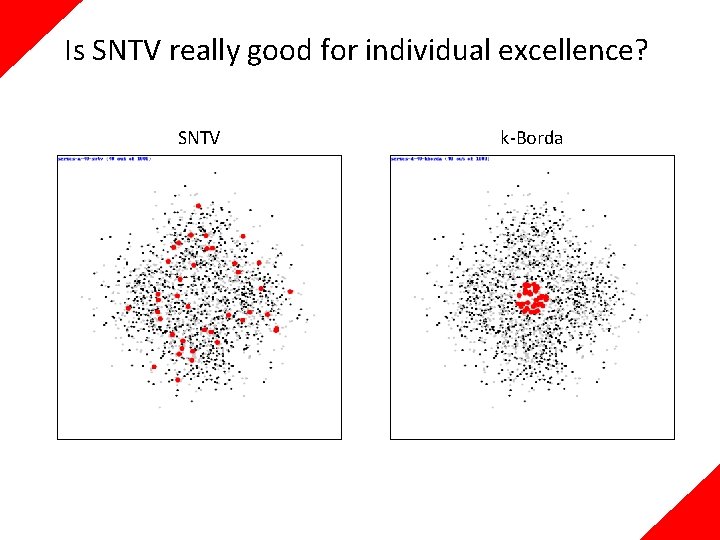
Is SNTV really good for individual excellence? SNTV k-Borda

Nature of the Committees (Diveristy/Coverage)

Applications Requiring Diversity/Coverage Instead of finding the “best” candidates (recall Excellence) we aim at covering all views of the electorate Some applications: Where to place facilities? Which products to produce? Which products to advertise?

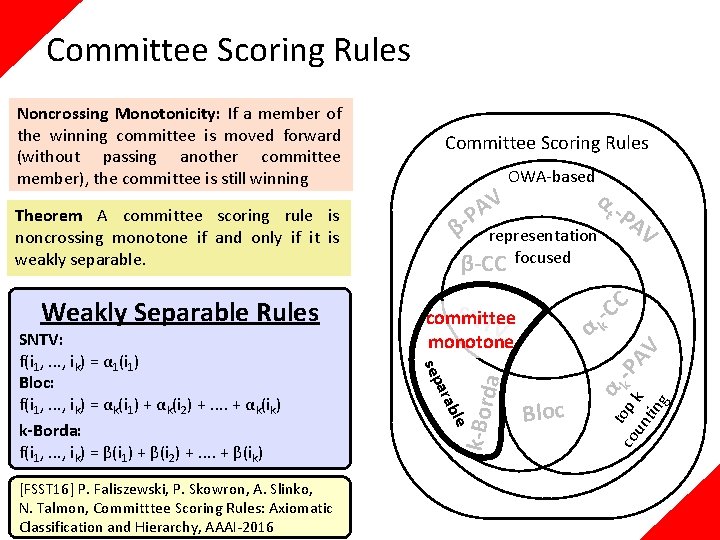
Axioms for Diversity: Narrow Top A rule satisfies the narrow top criterion if whenever there is a set W of k candidates such that each voter ranks first a member of W, then W is a winning committee 4 3 2 1 0 V 1: > > V 2: > > V 3: > > V 4: > > β-CC and SNTV β-CC satisfies narrow top k-Borda (e. g. , ) does not k-Borda : 10 : 8 : 4 SNTV : 2 E. Elkind, P. Faliszewski, P. Skowron, A. Slinko: Properties of Multiwinner Voting Rules, SC&W, 2017 : 0
![Axioms for Diversity Narrow Top FSST 16 P Faliszewski P Skowron A Slinko N Axioms for Diversity: Narrow Top [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N.](https://slidetodoc.com/presentation_image/5b478abf0b0c814ddc0fcc4dc05cbc58/image-54.jpg)
Axioms for Diversity: Narrow Top [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 α representation β-CC focused t -P AV narrow top SNT consistent -CC V αk y akl we rable a sep SNTV: f(i 1, . . . , ik) = α 1(i 1) β-CC: f(i 1, . . . , ik) = β(i 1) OWA-based Bloc α t o co p k -P un k AV tin g Representation-Focused Rules β- V A P da Theorem If a committee scoring rule is representation-focused then it is narrow-top consistent. Committee Scoring Rules k-Bor Narrow Top A rule satisfies the narrow top criterion if whenever there is a set W of k candidates such that each voter ranks first a member of W, then W is a winning committee

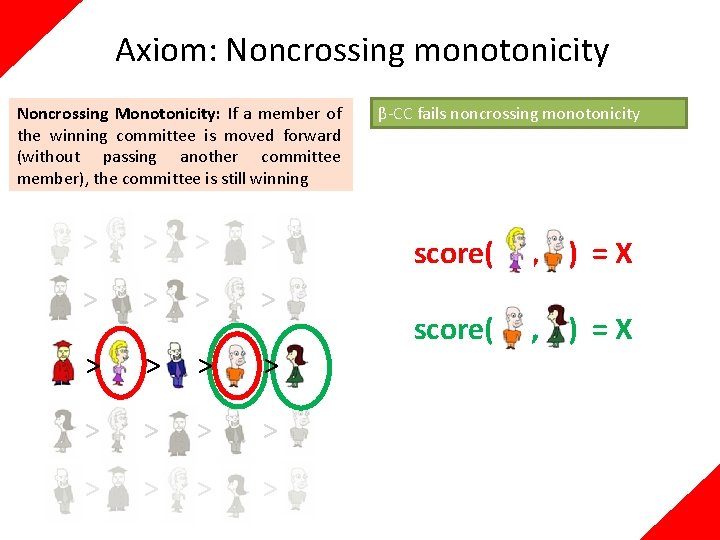
Axiom: Noncrossing monotonicity Noncrossing Monotonicity: If a member of the winning committee is moved forward (without passing another committee member), the committee is still winning > > > > > β-CC fails noncrossing monotonicity

Axiom: Noncrossing monotonicity Noncrossing Monotonicity: If a member of the winning committee is moved forward (without passing another committee member), the committee is still winning > > > > > β-CC fails noncrossing monotonicity score( , ) =X

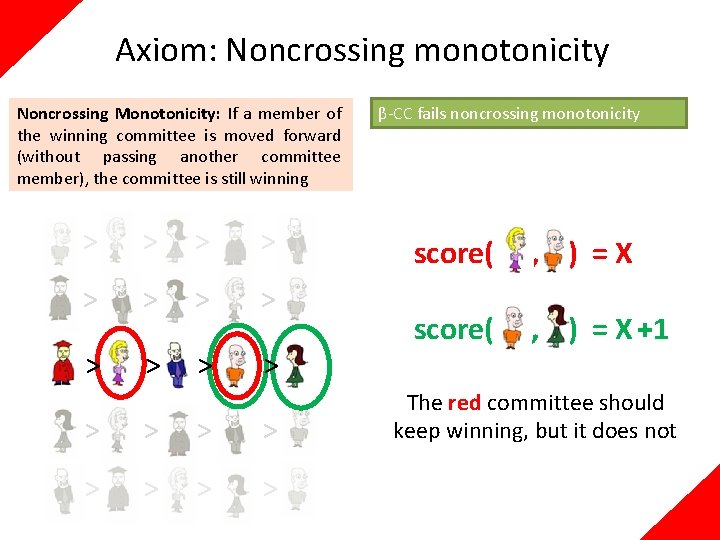
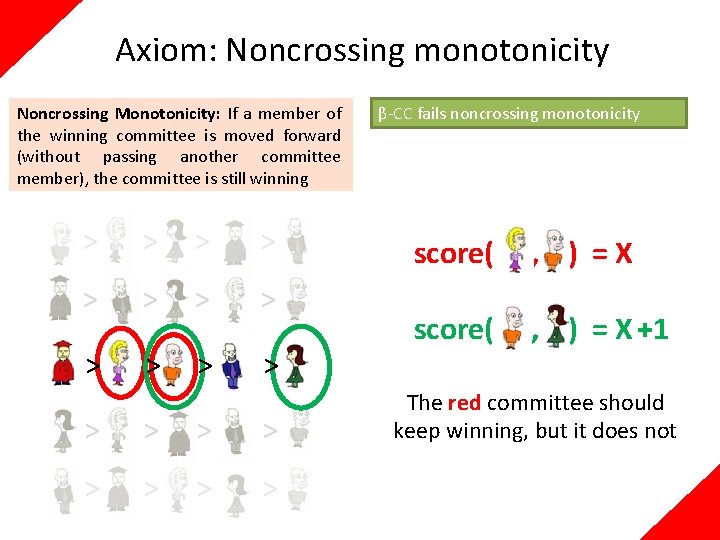
Axiom: Noncrossing monotonicity Noncrossing Monotonicity: If a member of the winning committee is moved forward (without passing another committee member), the committee is still winning > > > > > β-CC fails noncrossing monotonicity score( , ) =X score( , ) = X +1 The red committee should keep winning, but it does not

Axiom: Noncrossing monotonicity Noncrossing Monotonicity: If a member of the winning committee is moved forward (without passing another committee member), the committee is still winning > > > > > β-CC fails noncrossing monotonicity score( , ) =X score( , ) = X +1 The red committee should keep winning, but it does not

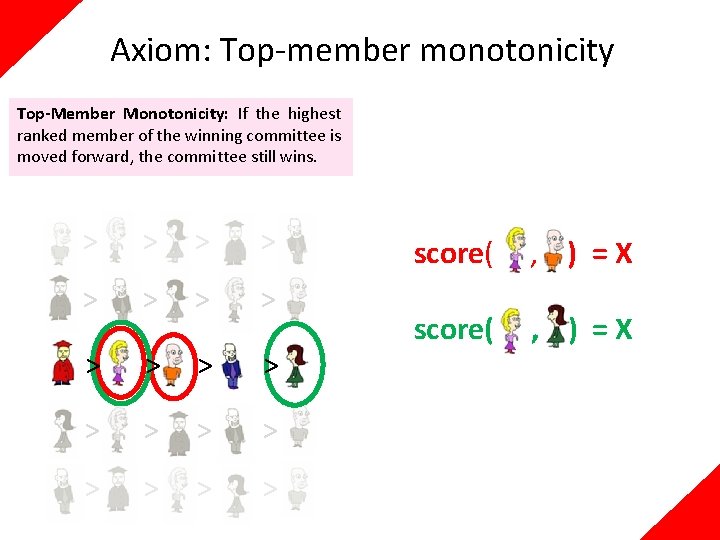
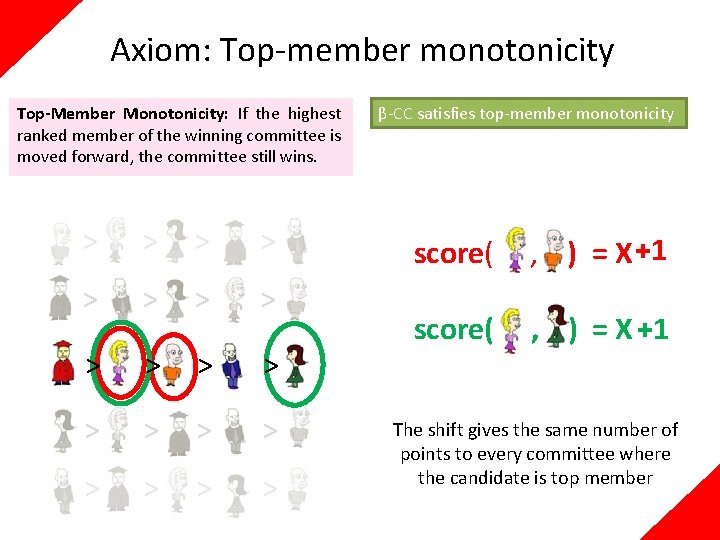
Axiom: Top-member monotonicity Top-Member Monotonicity: If the highest ranked member of the winning committee is moved forward, the committee still wins. > > > > > score( , ) =X

Axiom: Top-member monotonicity Top-Member Monotonicity: If the highest ranked member of the winning committee is moved forward, the committee still wins. > > > > > β-CC satisfies top-member monotonicity score( , ) = X +1 The shift gives the same number of points to every committee where the candidate is top member

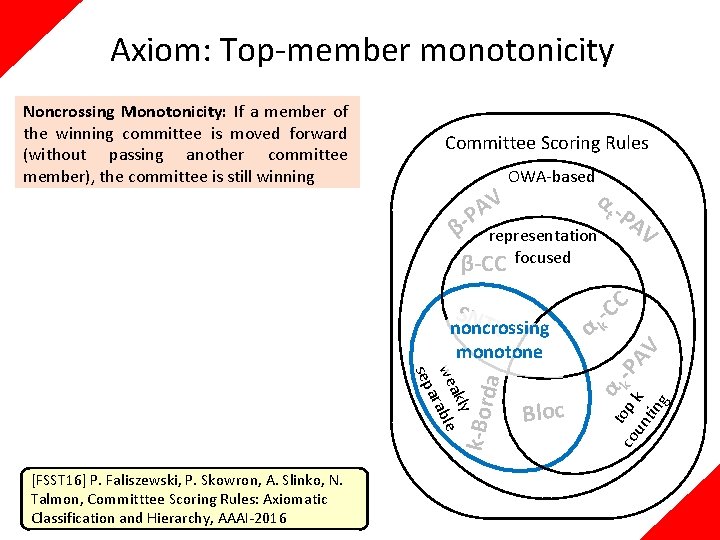
Axiom: Top-member monotonicity Noncrossing Monotonicity: If a member of the winning committee is moved forward (without passing another committee member), the committee is still winning Committee Scoring Rules β- V A P OWA-based α representation β-CC focused noncrossing V monotone k-Bor da y akl we rable a sep [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 Bloc α AV C -C k α t o co p k -P un k AV tin g SNT t -P

Axiom: Top-member monotonicity Top-Member Monotonicity: If the highest ranked member of the winning committee is moved forward, the committee still wins. Committee Scoring Rules OWA-based α V A t -P P β representation AV top-member focused β-CC monotone CC SNT noncrossing V αk monotone k-Bor da y akl we rable a sep [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 Bloc α t o co p k -P un k AV tin g Noncrossing Monotonicity: If a member of the winning committee is moved forward (without passing another committee member), the committee is still winning
![Axioms Narrow Top Top Member Monotonicity FSST 16 P Faliszewski P Skowron A Axioms: Narrow Top + Top Member Monotonicity [FSST 16] P. Faliszewski, P. Skowron, A.](https://slidetodoc.com/presentation_image/5b478abf0b0c814ddc0fcc4dc05cbc58/image-63.jpg)
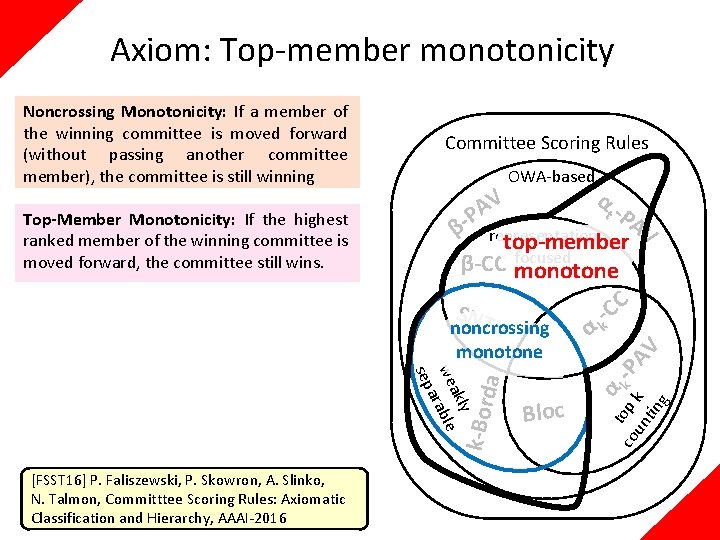
Axioms: Narrow Top + Top Member Monotonicity [FSST 16] P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Committtee Scoring Rules: Axiomatic Classification and Hierarchy, AAAI-2016 noncrossing Bloc monotone α t o co p k -P un k AV tin g α V A t -P P β representation AV top-member focused β-CC monotone SNTnarrow top -CC k V α consistent y akl we rable a sep Narrow Top A rule satisfies the narrow top criterion if whenever there is a set W of k candidates such that each voter ranks first a member of W, then W is a winning committee OWA-based da Top-Member Monotonicity: If the highest ranked member of the winning committee is moved forward, the committee still wins. Committee Scoring Rules k-Bor Noncrossing Monotonicity: If a member of the winning committee is moved forward (without passing another committee member), the committee is still winning

Axioms: Narrow Top + Top Member Monotonicity α t -P AV top-member + C C SNT k narrow topα V noncrossing Bloc monotone α t o co p k -P un k AV tin g Theorem A committee scoring rule is representation focused if and only if it is topmember monotone and consistent with the narrow-top principle. OWA-based representation β-CC focused y akl we rable a sep Narrow Top A rule satisfies the narrow top criterion if whenever there is a set W of k candidates such that each voter ranks first a member of W, then W is a winning committee β- V A P da Top-Member Monotonicity: If the highest ranked member of the winning committee is moved forward, the committee still wins. Committee Scoring Rules k-Bor Noncrossing Monotonicity: If a member of the winning committee is moved forward (without passing another committee member), the committee is still winning

Chamberlin—Courant is good for diversity

How to deal with hardness of Chamberlin —Courant?

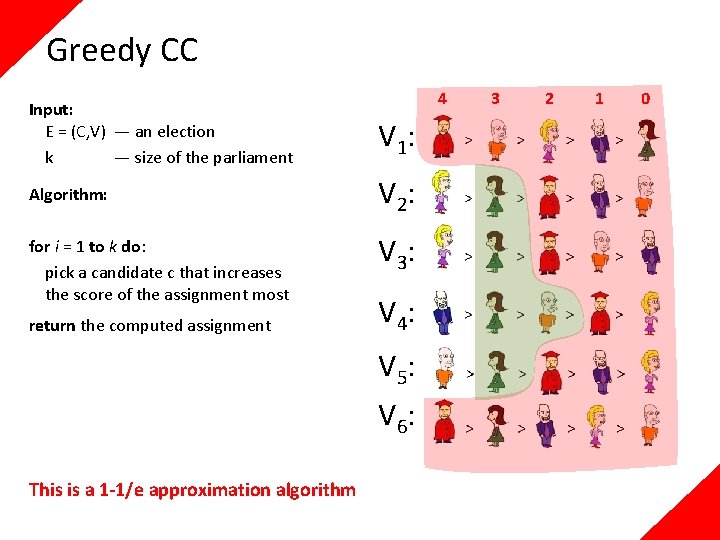
Greedy CC 4 Input: E = (C, V) — an election k — size of the parliament V 1 : Algorithm: V 2 : for i = 1 to k do: pick a candidate c that increases the score of the assignment most return the computed assignment V 3 : V 4 : V 5 : V 6 : This is a 1 -1/e approximation algorithm 3 2 1 0

Greedy CC 4 V 1 : V 2 : V 3 : V 4 : V 5 : V 6 : 3 2 1 0

CC Greedy. CC

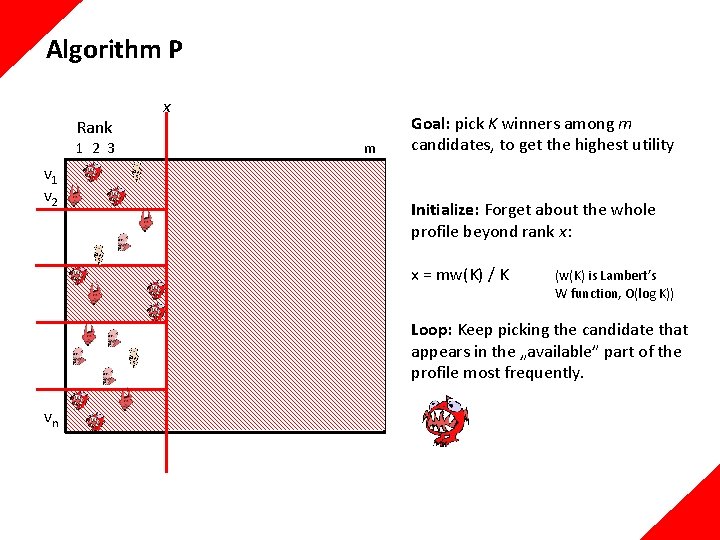
Algorithm P Rank 1 2 3 v 1 v 2 x m Goal: pick K winners among m candidates, to get the highest utility Initialize: Forget about the whole profile beyond rank x: x = mw(K) / K (w(K) is Lambert’s W function, O(log K)) Loop: Keep picking the candidate that appears in the „available” part of the profile most frequently. vn

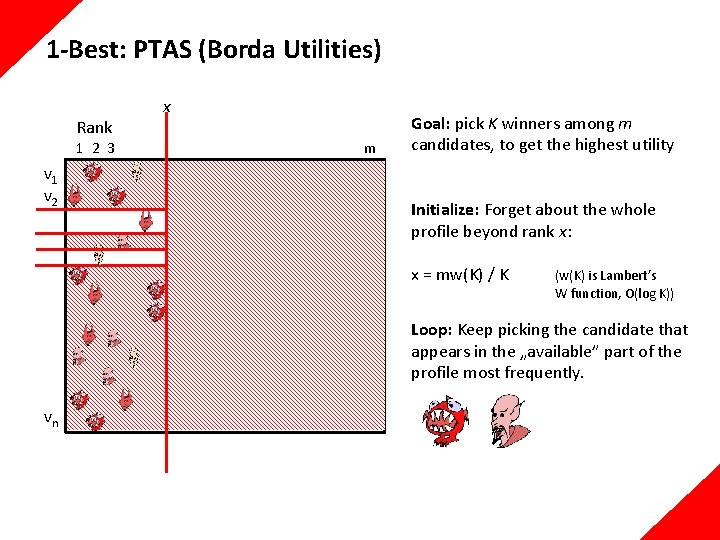
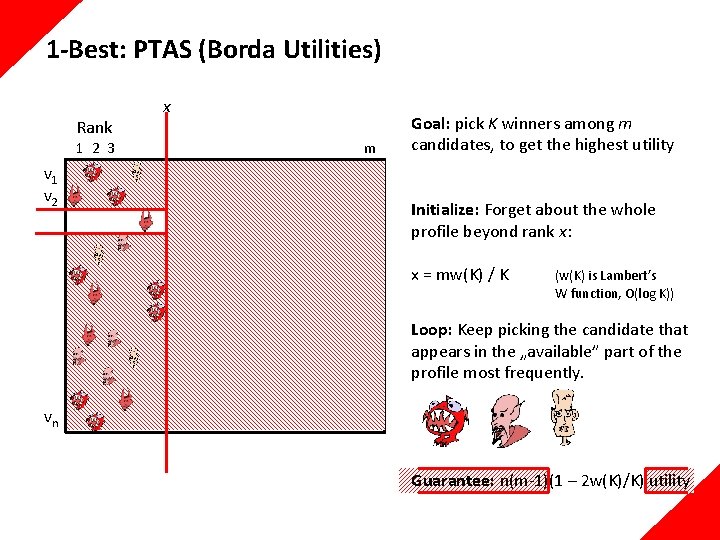
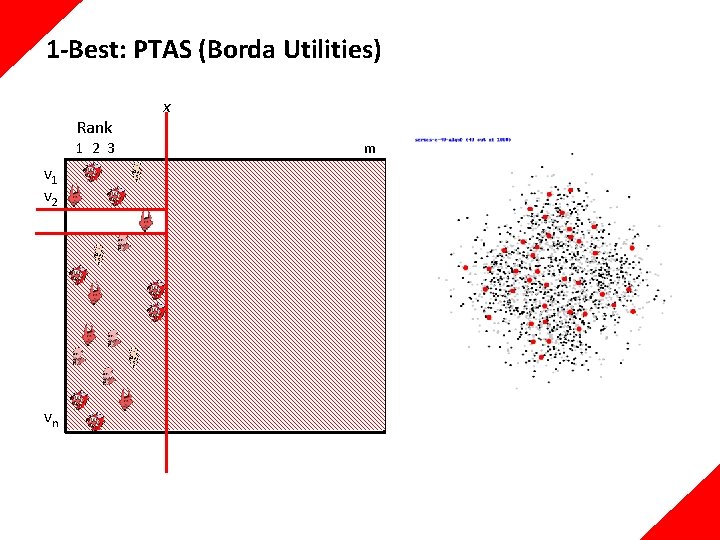
1 -Best: PTAS (Borda Utilities) Rank 1 2 3 v 1 v 2 x m Goal: pick K winners among m candidates, to get the highest utility Initialize: Forget about the whole profile beyond rank x: x = mw(K) / K (w(K) is Lambert’s W function, O(log K)) Loop: Keep picking the candidate that appears in the „available” part of the profile most frequently. vn

1 -Best: PTAS (Borda Utilities) Rank 1 2 3 v 1 v 2 x m Goal: pick K winners among m candidates, to get the highest utility Initialize: Forget about the whole profile beyond rank x: x = mw(K) / K (w(K) is Lambert’s W function, O(log K)) Loop: Keep picking the candidate that appears in the „available” part of the profile most frequently. vn Guarantee: n(m-1)(1 – 2 w(K)/K) utility

1 -Best: PTAS (Borda Utilities) Rank 1 2 3 v 1 v 2 vn x m

CC Greedy. CC Algorithm P

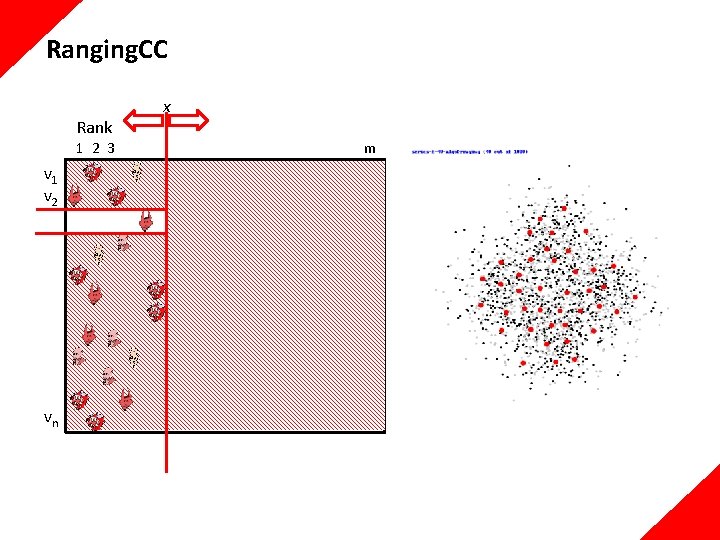
Ranging. CC Rank 1 2 3 v 1 v 2 vn x m

CC Greedy. CC Algorithm P Ranging. CC

Summary

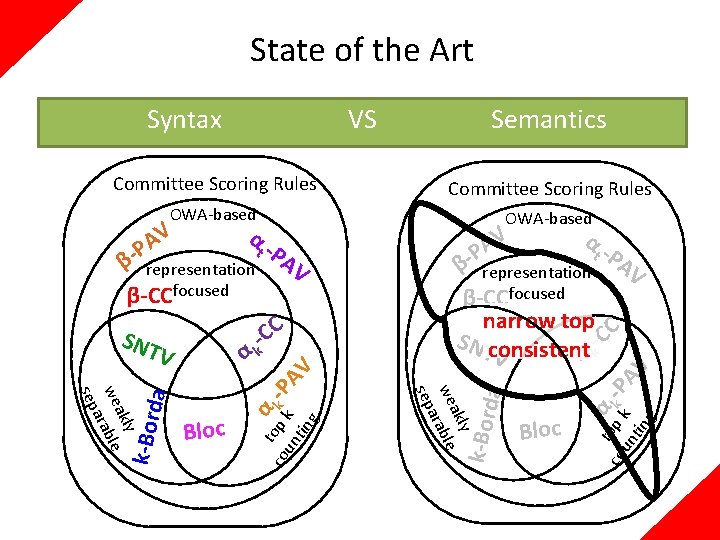
State of the Art Syntax VS Semantics Committee Scoring Rules OWA-based SNT da k-Bor t -P β representation AV β-CCfocused narrow top C SNTconsistent k-C α V y akl we rable a sep Bloc C -k C α co top k -P un k AV tin g α V AV α V A -P Bloc α t o co p k -P un k AV tin g representation β-CCfocused t -P da α k-Bor V A P β-

Take-Home Message s n o i t a c i l p y ap Man New sub-field Multiwinner Elections ics t a m e h t a Nice M

Thank You! https: //github. com/elektronaj/MW 2 D Multiwinner Voting: A New Challenge for Social Choice Theory, P. Faliszewski, P. Skowron, A. Slinko, N. Talmon, Trends in Computational Social Choice, 2017
 Piotr faliszewski
Piotr faliszewski Piotr faliszewski
Piotr faliszewski Piotr faliszewski
Piotr faliszewski Pros of fptp
Pros of fptp Imf functions
Imf functions Voting behaviour essay
Voting behaviour essay Voting rights
Voting rights Voting by feet tiebout
Voting by feet tiebout Hough voting
Hough voting Voting districts definition ap human geography
Voting districts definition ap human geography Sociological factors that affect voting behavior
Sociological factors that affect voting behavior Deployment diagram for online voting system
Deployment diagram for online voting system Block diagram of mobile phone
Block diagram of mobile phone Brainpop political parties
Brainpop political parties Sms poll voting
Sms poll voting Online voting system project proposal
Online voting system project proposal Hough voting
Hough voting Activity diagram for online voting system
Activity diagram for online voting system Which statement best summarizes the water cycle
Which statement best summarizes the water cycle Red line voting
Red line voting Meetoo voting
Meetoo voting Vevox voting
Vevox voting Ieee ou analytics
Ieee ou analytics Instant runoff voting excel template
Instant runoff voting excel template What are the four common methods of voting in ffa
What are the four common methods of voting in ffa Surveys, experiments, and observational studies worksheet
Surveys, experiments, and observational studies worksheet Survey vs observational study
Survey vs observational study 2k factorial experiments and fractions
2k factorial experiments and fractions Chapter 13 experiments and observational studies
Chapter 13 experiments and observational studies Miller and urey's experiments attempted to demonstrate
Miller and urey's experiments attempted to demonstrate Counting rule for multiple-step experiments
Counting rule for multiple-step experiments Pro cons animal testing
Pro cons animal testing Torrent qq
Torrent qq![[http://earthobservatory.nasa.gov/experiments/biome/] [http://earthobservatory.nasa.gov/experiments/biome/]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20200%20200%22%3E%3C/svg%3E) [http://earthobservatory.nasa.gov/experiments/biome/]
[http://earthobservatory.nasa.gov/experiments/biome/] Test your hypothesis
Test your hypothesis Jean piaget 1896 a 1980
Jean piaget 1896 a 1980 A balanced outlook on law
A balanced outlook on law Science experiments for highschool
Science experiments for highschool Eyewitness testimony video experiments
Eyewitness testimony video experiments Computer science experiments
Computer science experiments Czech experiments
Czech experiments Griffith’s transformation experiments
Griffith’s transformation experiments Design of experiments doe
Design of experiments doe In his transformation experiments what did griffith observe
In his transformation experiments what did griffith observe Merit and demerit of standard deviation
Merit and demerit of standard deviation Jmp factorial design
Jmp factorial design Examples of binomial experiments
Examples of binomial experiments Iit kharagpur virtual lab computer organization
Iit kharagpur virtual lab computer organization Francis cecil sumner, ph.d.
Francis cecil sumner, ph.d. Barbara herbert and daphne goodship
Barbara herbert and daphne goodship Construction studies portfolio
Construction studies portfolio Core flooding experiment
Core flooding experiment Bank wiring experiment
Bank wiring experiment Full factorial design
Full factorial design Design of experiments quality management pmp
Design of experiments quality management pmp Experiments in goodness
Experiments in goodness Colorimetry experiments
Colorimetry experiments Counting rule for multiple-step experiments
Counting rule for multiple-step experiments Abnormal psychology experiments
Abnormal psychology experiments Paper presentation design
Paper presentation design Taguchi design of experiments
Taguchi design of experiments Why is “replication key” psychology experiments?
Why is “replication key” psychology experiments? If an acid is splashed on your skin, wash at once with
If an acid is splashed on your skin, wash at once with Difference between observational and experimental study
Difference between observational and experimental study Pvt sample
Pvt sample Chapter 2 american experiments summary
Chapter 2 american experiments summary Why are controlled experiments sometimes impossible
Why are controlled experiments sometimes impossible Pmp stakeholder engagement plan
Pmp stakeholder engagement plan Liz sneddon bivariate
Liz sneddon bivariate Split brain experiments
Split brain experiments Integrated science labs
Integrated science labs Plackett burman method
Plackett burman method Viking experiments
Viking experiments Checklist for good practices in laboratory experiments
Checklist for good practices in laboratory experiments Science risk assessment primary school
Science risk assessment primary school Design of experiments voorbeeld
Design of experiments voorbeeld Tom campbell experiments
Tom campbell experiments Design of experiments
Design of experiments Rerandomization to improve covariate balance in experiments
Rerandomization to improve covariate balance in experiments Radial heat conduction experiment report
Radial heat conduction experiment report 3 laws of inheritance
3 laws of inheritance
































![[http://earthobservatory.nasa.gov/experiments/biome/] [http://earthobservatory.nasa.gov/experiments/biome/]](https://slidetodoc.com/wp-content/uploads/2020/11/1537165_35fb5ecc588217ed14768e866616d64b-300x169.jpg)