Introduction to CS Theory Lecture 1 Introduction Piotr

Introduction to CS Theory Lecture 1 – Introduction Piotr Faliszewski pf@cs. rit. edu

Introduction o Instructor n n n o Course website: n o Piotr Faliszewski Office: 70 -3575 Email: pf@cs. rit. edu http: //www. cs. rit. edu/~pf/theory/ Office hours n n Monday through Thursday 2 pm— 4 pm

Logistics o Look at the courses website! o Important highlights n Cooperation on homeworks o o n n Quizzes! Disputing your grade o o Teams of two allowed Both people get the same grade—you cannot complain about your teammate not working At most a week after you received the grade Discrete math quiz n Next Monday

Introduction o This is a course in mathematics! n Basic discrete math o o o Dealing with sets, functions, sequences etc. Logic Inductive proofs (!!!) You should already be familiar with those, but we will review a bit as well o Goals of the course n n n Understand the nature of computation Develop problem solving skills Increase mathematical sophistication

Computer Science Needs Precision! From a letter of Charles Babbage to Alfred Tennyson in response to his poem "The Vision of Sin“: "In your otherwise beautiful poem, one verse reads, Every moment dies a man, Every moment one is born. . If this were true, the population of the world would be at a standstill. In truth, the rate of birth is slightly in excess of that of death. I would suggest: Every moment dies a man, Every moment 1 1/16 is born. Strictly speaking, the actual figure is so long I cannot get it into a line, but I believe the figure 1 1/16 will be sufficiently accurate for poetry. "

What is this course about? o Two fundamental questions about computation n n What can and cannot be computed? What can and cannot be computed efficiently? o What is computation? n o But, before we can answer these… n n What IS computation? What PROBLEMS do we want to solve? Many different models of a computer o o Finite automata Push-down automata Turing machines Decision problems and languages

Languages and Decision Problems o Decision problem n n Name Input o n Question o o the mathematical entities about whose properties we ask A well-defined yes/no question Language n n A set of strings Languages encode decision problems o Example n n n Name: Connectivity Input: Graph G, vertices s and t Question: Are vertices s and t connected in G

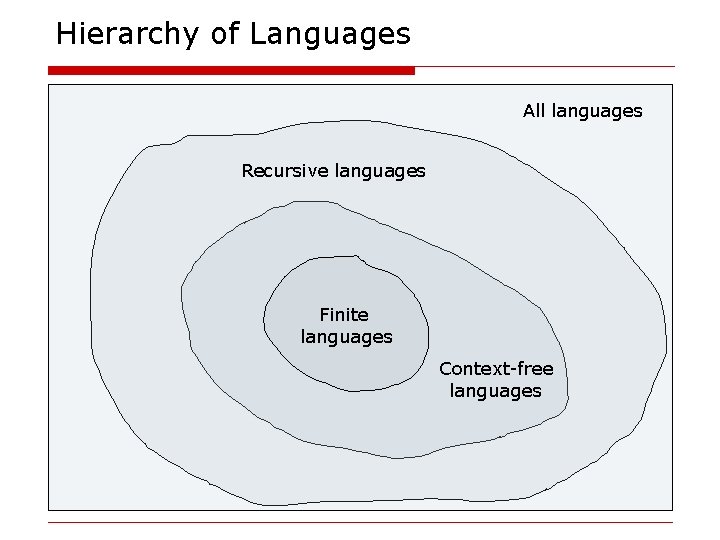
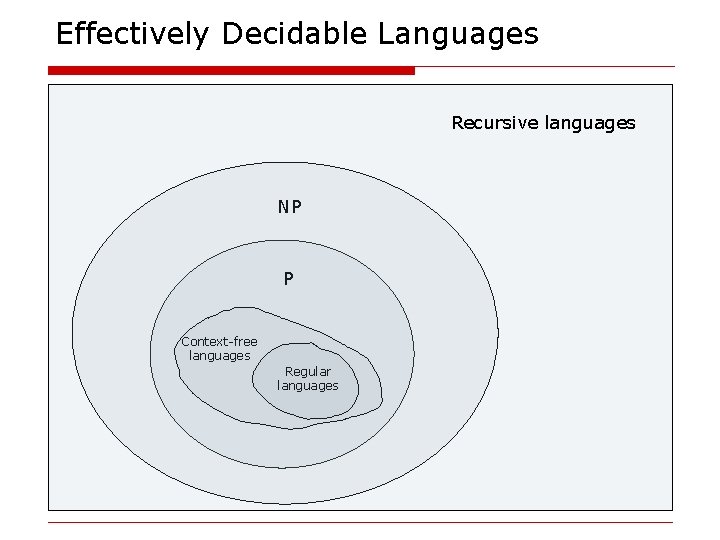
Languages and Decision Problems o Our two fundamental questions n n What decision problems can and cannot be solved? What decision problem can and cannot be solved efficiently o We focus on languages o Chomsky Hierarchy o Models of computation n Regular languages / finite automata Context-free languages / push-down automata Turing machines

Hierarchy of Languages All languages Recursive languages Finite languages Context-free languages

Effectively Decidable Languages Recursive languages NP P Context-free languages Regular languages

And now… o Let’s get some real work done! n n Your responsibility: Part I of the book But, I will cover: o o Languages Mathematical induction

1. 5 Languages o Language n o A set of strings over some alphabet o String n Alphabet n n A finite set of indivisible objects, usually denoted as Σ Examples o o {0, 1, 2, …, 9} {0, 1} {a, b, c, …, z} {1} n A string over Σ is a finite, possibly empty, sequence of elements of Σ Some strings over {0, 1}: o o n Examples of nonstrings (for alphabet {0, 1}) o o n ε empty string 0, 1, 001, 0101 012011 11111… Length of a string x o o |x| Examples?

Defining Languages o Set of all strings Σ* -- set of all strings over Σ {0, 1}* {a}* n n n o We can define languages via set operations n n n Intersection, union Difference Complement operation o o L = Σ* - L Examples of languages L 1 L 2 L 3 L 4 = = { x {0, 1}* | x contains at least as many 0 s as 1 s} { x {0, 1}* | x contains at least as many 1 s as 0 s} {ε} { x {0, 1}* | x viewed as an integer is a prime} L 5 = L 1 L 2 L 6 = L 1

Operations on Strings Let x, y Σ* Some operations on strings n n n xy – concatenation xi – concatenation of x i times with itself x is a substring of y if there are strings w and z such that y=wxz o Examples n n n x is a prefix of y if there is a string z such that y=xz n x is a suffix of y if there is a string z such that y=zx n n n x = ab y = aabb xy = abaabb xε = x = εx x 3 = xxx = ababab x 0 = ? ? ? x is a substring of y z = bb z is a suffix of y x is a prefix of x

Operations on Languages o Let L, L 1, L 2 be languages over the same alphabet Σ n n L 1 L 2 = {xy | x in L 1 and y in L 2} – the concatenation of two languages Li – concatenation of i L’s o n o What is L 0? L* = L 0 L 1 L 2 L 3 … Kleene’s star L+ = LL* = L*L Exercises n n n Is there a language L such that L* is finite? Let L 1, L 2 be two finite languages. What is the cardinality of L 1 L 2 Is there a language such that L = L*?

Mathematical Induction o Mathematical induction n n o Inductive proof: n n o Technique to prove facts about finite entities E. g. , properties of integers Base case Inductive step Intuition n … a little like a for loop in a program: we construct the proof in iterations. Theorem. Let A be a finite set with n elements. There are 2 n distinct subsets of A. Proof. Base: A = Inductive step: Assume that theorem holds for all natural numbers up to k. Let A be a set with k+1 elements and B an arbitrary subset of k elements of A. Let x be such that: A = B {x} By the inductive assumption, B has 2 k subsets. Thus A has 2 k+1 subsets. (Why? )

Mathematical Induction – Examples o Let us prove the following: n n Σ = {0, 1}, each string x such that x = 0 y 1, where y Σ*, contains 01 as a substring For every natural number n, n ≥ 2, n either is a prime or a product of two or more primes o How about the following theorem: n For every natural number n it holds that n! > 2 n And I can prove by induction that all horses are of the same color!

Recursive Definitions o Recursive definition n Define a small set of basic entities Show to obtain larger ones from those already constructed n A bit like induction! n Examples Factorial 0! = 1 For each natural n, (n+1)! = (n+1)*n! Recursive definition of Σ*: 1. ε Σ* 2. If x Σ* and a Σ then xa Σ* 3. Nothing is in Σ* unless it is obtained by the two previous rules.

Recursive Definitions – Examples o Two exercises n o Give a recursive definition of the length of a string. Palindromes n n n Give a recursive definition of a reverse of a string. Hmm… This looks wrong to me! o A string is a palindrome if it reads the same backward and forward Let’s define a language of palindromes! Language L of palindromes, Σ = {a, b}. 1. 2. 3. ε L If x L then both axa and bxb belong to L. Nothing belongs to L unless it is obtained by rules 1 and 2.

Recursive Definitions – Examples o Language L of all strings with as many 0 s as 1 s. (Σ = {0, 1}) 1. 2. ε L For any x in L it holds that each of: 0 x 1 2. 1 x 0 3. 01 x 4. 10 x 5. x 01 6. x 10 belongs to L. 1. Is this definition correct? o Exercise n Prove that for each string x over alphabet Σ it holds that |x| = |xr| xr is the reverse of x n Structural induction! n