Multiplicative weights method A meta algorithm with applications

Multiplicative weights method: A meta algorithm with applications to linear and semi-definite programming Sanjeev Arora Princeton University Based upon: Fast algorithms for Approximate SDP [FOCS ‘ 05] log(n) approximation to SPARSEST CUT in Õ(n 2) time [FOCS ‘ 04] The multiplicative weights update method and it’s applications [’ 05] See also recent papers by Hazan and Kale.

Multiplicative update rule (long history) n agents weights w 1 w 2. . . Update weights according to performance: wit+1 Ã wit (1 + ¢ performance of i) wn Applications: approximate solutions to LPs and SDPs, flow problems, online learning (boosting), derandomization & chernoff bounds, online convex optimization, computational geometry, metricembeddongs, portfolio management… (see our survey)

Simplest setting – predicting the market 1$ for correct prediction 0$ for incorrect N “experts” on TV Can we perform as good as the best expert ?

Weighted majority algorithm [LW ‘ 94] “Predict according to the weighted majority. ” Multiplicative update (initially all wi =1): If expert predicted correctly: wit+1 Ã wit If incorrectly, wit+1 Ã wit(1 - ) Claim: #mistakes by algorithm ¼ 2(1+ )(#mistakes by best expert) Potential: t = Sum of weights= i wit (initially n) If algorithm predicts incorrectly ) t+1 · t - t /2 T · (1 - /2)m(A) n m(A) =# mistakes by algorithm T ¸ (1 - )mi ) m(A) · 2(1+ )mi + O(log n/ )

Generalized Weighted majority [A. , Hazan, Kale ‘ 05] n agents Set of events (possibly infinite) event j expert i payoff M(i, j)

Generalized Weighted majority [AHK ‘ 05] Set of events (possibly infinite) n agents p 1 p 2. . . pn Algorithm: plays distribution on experts (p 1, …, pn) Payoff for event j: i pi M(i, j) Update rule: pit+1 Ã pit (1 + ¢ M(i, j)) Claim: After T iterations, Algorithm payoff ¸ (1 - ) best expert – O(log n / )

Game playing, Online optimization Lagrangean relaxation Gradient descent Chernoff bounds Games with Matrix Payoffs Boosting Fast soln to LPs, SDPs

Common features of MW algorithms “competition” amongst n experts Appearance of terms like exp( - t (performance at time t) ) Time to get -approximate solutions is proportional to 1/ 2.

Boosting and Ada. Boost (Schapire’ 91, Freund-Schapire’ 97) “Weak learning ) Strong learning” Input: 0/1 vectors with a “Yes/No” label (white, tall, vegetarian, smoker, …, ) “Has disease” (nonwhite, short, vegetarian, nonsmoker, . . ) “No disease” Desired: Short OR-of-AND (i. e. , DNF) formula that describes fraction of data (if one exists) (white Æ vegetarian) Ç (nonwhite Æ nonsmoker) = 1 - “Strong Learning” = ½ + “Weak Learning” Main idea in boosting: data points are “experts”, weak learners are “events. ”

Approximate solutions to convex programming e. g. , Plotkin Shmoys Tardos ’ 91, Young’ 97, Garg Koenemann’ 99, Fleischer’ 99 MW Meta-Algorithm gives unified view Note: Distribution { pi} i pi =1 $ Convex Combination If P is a convex set and each xi 2 P then i pi xi 2 P

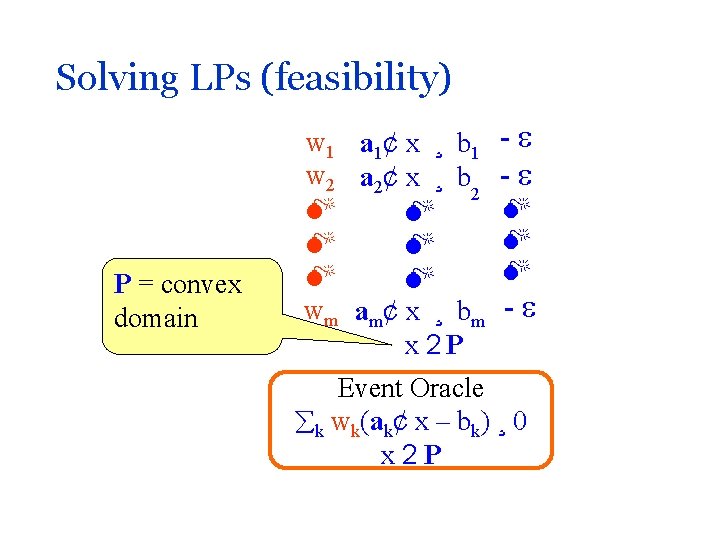
Solving LPs (feasibility) P = convex domain w 1 a 1¢ x ¸ b 1 w 2 a 2¢ x ¸ b 2 wm am¢ x ¸ bm x 2 P - - Event Oracle k wk(ak¢ x – bk) ¸ 0 x 2 P

Solving LPs (feasibility) [1 – (a 1 ¢ x 0 – b 1)/ ] £ w 1 a 1¢ x ¸ b 1 [1 – (a 2 ¢ x 0 – b 2)/ ] £ w 2 a 2¢ x ¸ b 2 Final solution = Average x vector [1 – (am ¢ x 0 – bm)/ ] £ wm am¢ x ¸ bm x 2 P x 0 Oracle |ak ¢ x 0 – bk| · = width k wk(ak¢ x – bk) ¸ 0 x 2 P

Performance guarantees In O( 2 log(n)/ 2) iterations, average x is feasible. Packing-Covering LPs: [Plotkin, Shmoys, Tardos ’ 91] 9? x 2 P: j = 1, 2, … m: aj ¢ x ¸ 1 Covering problem Want to find x 2 P s. t. aj ¢ x ¸ 1 - Assume: 8 x 2 P: 0 · aj ¢ x · MW algorithm gets feasible x in O( log(n)/ 2) iterations

Connection to Chernoff bounds and derandomization Deterministic approximation algorithms for 0/1 packing/covering problem a la Raghavan-Thompson Solve LP relaxation of integer program. Obtain soln (yi) Randomized Rounding O(log n) times) xi à 1 w/ prob. yi xi à 0 w/ prob. 1 - yi Derandomize using pessimistic estimators exp( i t ¢ f(yi)) without solving the LP. ” Young [95] “Randomized rounding MW update rule mimics pessimistic estimator.

Application 2: Semidefinite programming (Klein-Lu’ 97) a 1¢ x ¸ b 1 a 2¢ x ¸ b 2 am¢ x ¸ bm x 2 P aj and x : symmetric matrices in Rn £ n P= Oracle: max j wj (aj ¢ x) over P (eigenvalue computation!) {x: x is psd; tr(x) =1}

The promise of SDPs… 0. 878 -approximation to MAX-CUT (GW’ 94), 7/8 -approximation to MAX-3 SAT (KZ’ 00) plog n –approximation to SPARSEST CUT, BALANCED SEPARATOR (ARV’ 04). plog n-approximation to MIN-2 CNF DELETION, MIN-UNCUT (ACMM’ 05), MIN-VERTEX SEPARATOR (FHL’ 06), … etc…. The pitfall… High running times ---as high as n 4. 5 in recent works

Solving SDP relaxations more efficiently using MW [AHK’ 05] Problem Using Interior Point MAXQP (e. g. MAX-CUT) Õ(n 3. 5) Our result Õ(n 1. 5 N/ 2. 5) or Õ(n 3/ * 3. 5) HAPLOFREQ Õ(n 4) Õ(n 2. 5/ 2. 5) SCP Õ(n 4) Õ(n 1. 5 N/ 4. 5) EMBEDDING Õ(n 4) Õ(n 3/d 5 3. 5) SPARSEST CUT Õ(n 4. 5) Õ(n 3/ 2) MIN UNCUT etc Õ(n 4. 5) Õ(n 3. 5/ 2)

Key difference between efficient and not-so-efficient implementations of the MW idea: Width management. (e. g. , the difference between PST’ 91 and GK’ 99)

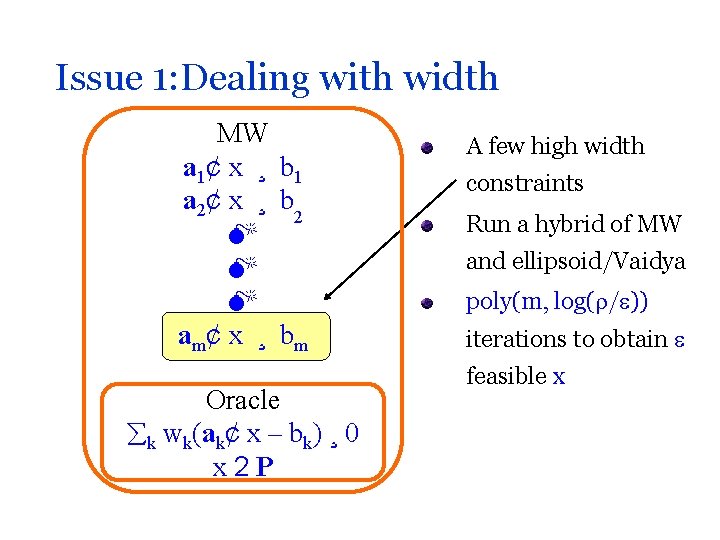
Recall: issue of width MW a 1¢ x ¸ b 1 a 2¢ x ¸ b 2 am¢ x ¸ bm Oracle k wk(ak¢ x – bk) ¸ 0 x 2 P Õ( 2/ 2) iterations to obtain feasible x = maxk |ak ¢ x – bk | is too large!!

Issue 1: Dealing with width MW a 1¢ x ¸ b 1 a 2¢ x ¸ b 2 am¢ x ¸ bm Oracle k wk(ak¢ x – bk) ¸ 0 x 2 P A few high width constraints Run a hybrid of MW and ellipsoid/Vaidya poly(m, log( / )) iterations to obtain feasible x

Dealing with width (contd) MW a 1¢ x ¸ b 1 a 2¢ x ¸ b 2 Dual ellipsoid/Vaidya am¢ x ¸ bm Oracle k wk(ak¢ x – bk) ¸ 0 x 2 P Hybrid of MW and Vaidya Õ( L 2/ 2) iterations to obtain feasible x L ¿

Issue 2: Efficient implementation of Oracle: fast eigenvalues via matrix sparsification Random sampling C C’ O( n ij|Cij|/ ) non-zero entries k C – C’k · Lanczos algorithm effectively uses sparsity of C Similar to Achlioptas, Mc. Sherry [’ 01], but better in some situations (also easier analysis)

O(n 2)-time algorithm to compute O(plog n)-approximation to SPARSEST CUT [A. , Hazan, Kale ’ 04] (combinatorial algorithm; improves upon O(n 4. 5) algorithm of A, Rao, Vazirani)

Sparsest Cut (G) = 2/5 S The sparsest cut: S O(log n) approximation [Leighton Rao ’ 88] O(plog n) approximation [A. , Rao, Vazirani’ 04] O(p log n) approximation in O(n 2) time. (Actually, finds expander flows) [A. , Hazan, Kale’ 05]

MW algorithm to find expander flows Events – { (s, w, z) | weights on vertices, edges, cuts} Experts – pairs of vertices (i, j) Payoff: (for weights di, j on experts) shortest path according to weights we Fact: If events are chosen optimally, the distribution on experts di, j converges to a demand graph which is an “expander flow” Cuts separating i and j [by results of Arora-Rao-Vazirani ’ 04 suffices to produce approx. sparsest cut]

New: Online games with matrix payoffs (joint w/ Satyen Kale’ 06) Payoff is a matrix, and so is the “distribution” on experts! Uses matrix analogues of usual inequalities 1+ x · ex I + A · e. A Can be used to give a new “primal-dual” view of SDP relaxations () easier, faster approximation algorithms)

New: Faster algorithms for online learning and portfolio management (Agarwal-Hazan’ 06, Agarwal-Hazan-Kalai-Kale’ 06 ) Framework for online optimization inspired by Newton’s method (2 nd order optimization). (Note: MW ¼ gradient descent) Fast algorithms for Portfolio management and other online optimization problems

Open problems Better approaches to width management? Faster run times? Lower bounds? THANK YOU

Connection to Chernoff bounds and derandomization Deterministic approximation algorithms a la Raghavan-Thompson Packing/covering IP with variables xi = 0/1 9? x 2 P: 8 j 2 [m], fj(x) ¸ 0 Solve LP relaxation using variables yi 2 [0, 1] Randomized rounding: 1 w. p. yi xi = 0 w. p. 1 – yi Chernoff: O(log m) sampling iterations suffice

Derandomization [Young, ’ 95] Can derandomize the rounding using exp(t j fj(x)) as a pessimistic estimator of failure probability By minimizing the estimator in every iteration, we mimic the random expt, so O(log m) iterations suffice The structure of the estimator obviates the need to solve the LP: Randomized rounding without solving the Linear Program Punchline: resulting algorithm is the MW algorithm!

Weighted majority [LW ‘ 94] If lost at t, t+1 · (1 -½ ) t At time T: T · (1 -½ )#mistakes ¢ 0 Overall: #mistakes · log(n)/ + (1+ ) mi #mistakes of expert i

Semidefinite programming Vectors aj and x: symmetric matrices in Rn £ n xº 0 Assume: Tr(x) · 1 Set P = {x: x º 0, Tr(x) · 1} Oracle: max j wj(aj ¢ x) over P Optimum: x = vv. T where v is the largest eigenvector of j wj a j

Efficiently implementing the oracle Optimum: x = vv. T v is the largest eigenvector of some matrix C Suffices to find a vector v such that v. TCv ¸ 0 Lanczos algorithm with a random starting vector is ideal for this Advantage: uses only matrix-vector products Exploits sparsity (also: sparsification procedure) Use analysis of Kuczynski and Wozniakowski [’ 92]