Algorithms in Action The Multiplicative Weights Update Method

Algorithms in Action The Multiplicative Weights Update Method Haim Kaplan, Uri Zwick Tel Aviv University May 2016 Last updated: June 7, 2017 1

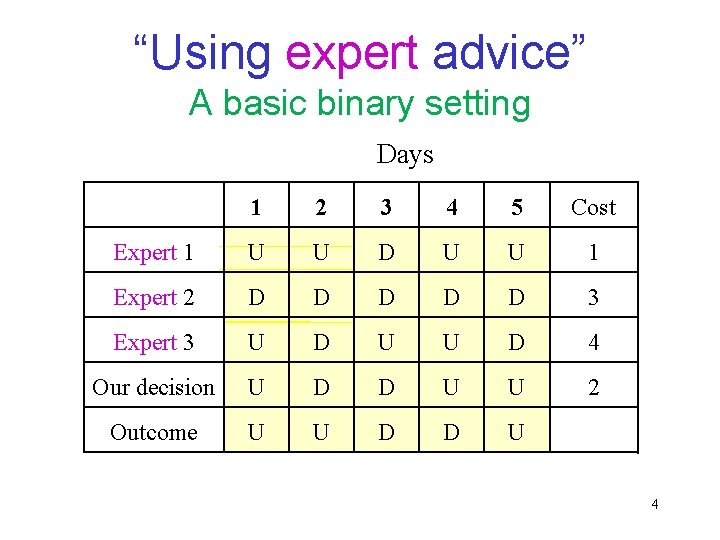
“Using expert advice” A basic binary setting We need to make a binary decision (Up/Down). Based on their advice, we make a choice. We then find out whether our choice is correct. If our choice is wrong, we pay a penalty of 1. If our choice is right, we do not pay anything. Our goal, of course, is to pay as little as possible. 2

“Using expert advice” A basic binary setting Days 1 2 3 4 5 Cost Expert 1 U U D U U 1 Expert 2 D D D 3 Expert 3 U D U U D 4 Our decision U D D U U 2 Outcome U U D D U 4

“Using expert advice” A basic binary setting How well can we do? If all “experts” are bad, we cannot do too well. We would like to do almost as well as the best expert, with hindsight. 5

The Weighted Majority algorithm [Littlestone-Warmuth (1994)] 6

The Weighted Majority algorithm [Littlestone-Warmuth (1994)] In particular, the inequality holds for the best expert. Thus, the cost of the Weighted Majority algorithm is only slightly larger than twice the cost of the best expert! (We can do even better using a randomized algorithm. ) 7

The Weighted Majority algorithm [Littlestone-Warmuth (1994)] Proof: 8

The Weighted Majority algorithm [Littlestone-Warmuth (1994)] 9

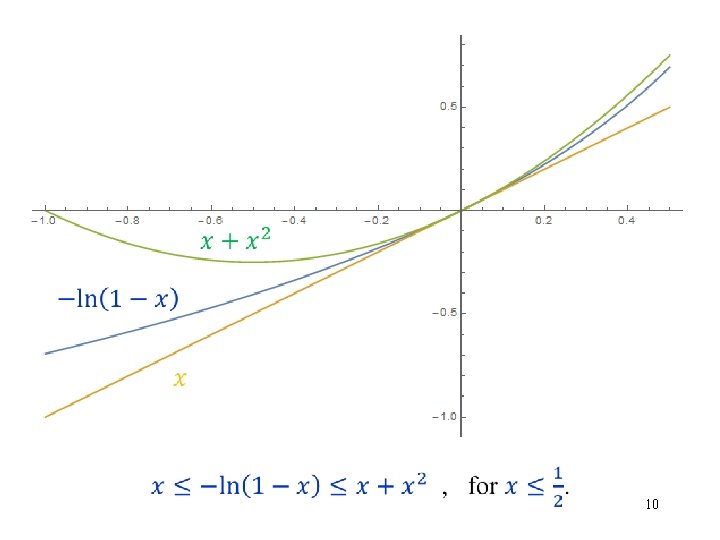
10

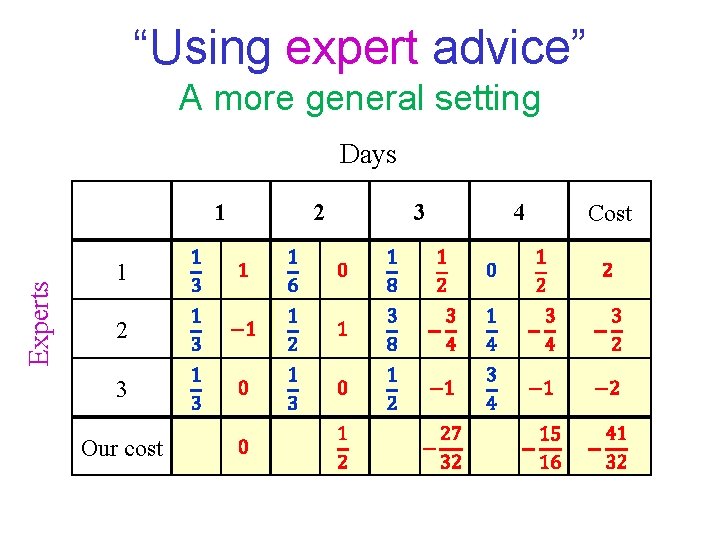
“Using expert advice” A more general setting We choose a (probability) distribution over the experts. We pay the average cost according to the distribution chosen. Our goal is to minimize our total cost. Alternative interpretation: On each day a random expert is drawn according to the distribution chosen. We pay the expected cost.

“Using expert advice” A more general setting Days Experts 1 1 2 3 Our cost 2 3 4 Cost

The Multiplicative Weights algorithm [Cesa-Bianchi, Mansour, Stoltz (2007)] 14

The Multiplicative Weights algorithm [Cesa-Bianchi, Mansour, Stoltz (2007)] 15

The Multiplicative Weights algorithm [Cesa-Bianchi, Mansour, Stoltz (2007)]

Applications of the Multiplicative Weights algorithm Learning a linear classifier (The Winnow algorithm) Boosting the performance of weak learners (cf. Adaboost) Approximately solving 0 -sum 2 -player games Approximately solving packing Linear Programs Approximately solving covering Linear Programs Special case: Multicommodity flow Approximately solving Semidefinte Programs Special case: SDP relaxation of MAX CUT … 17

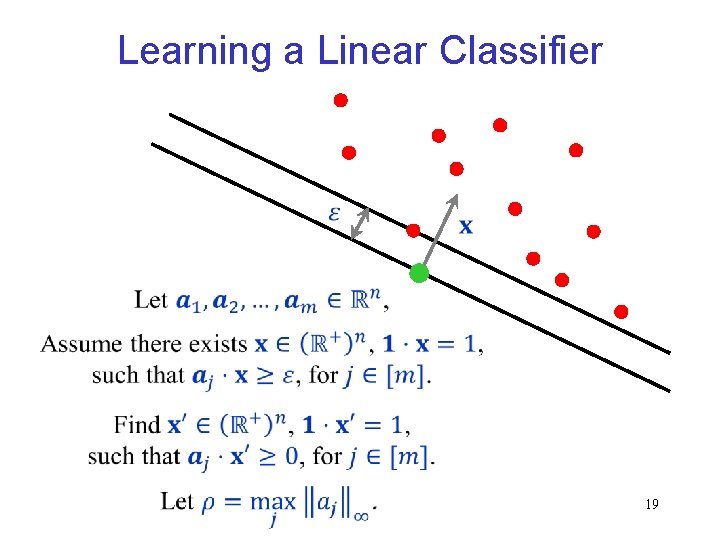
Learning a Linear Classifier 18

Learning a Linear Classifier 19

Learning a Linear Classifier The Winnow algorithm [Littlestone (1987)] Experts correspond coordinates (also known as features). 20

Learning a Linear Classifier The Winnow algorithm [Littlestone (1987)] 21

The Winnow algorithm [Littlestone (1987)] 22

0 -sum 2 -player matrix games No player wants to go first… Suppose the players play simultaneously. Playing deterministically is similar to playing first. Use randomized (mixed) strategies. 23

0 -sum 2 -player matrix games 24

0 -sum 2 -player matrix games Von Neumann’s min-max theorem: LP Duality 25

0 -sum 2 -player matrix games What is the value and what are the optimal strategies? value = 1 26

Solving 0 -sum games approximately Value and optimal strategies can be found by solving an LP. Can be done in polynomial time, but relatively slowly. In many situations a good approximation is sufficient. 27

0 -sum games using Multiplicative Updates [Freund-Schapire (1999)] A distribution over the experts is a mixed strategy for ROW. 28

0 -sum games using Multiplicative Updates [Freund-Schapire (1999)] 29

0 -sum games using Multiplicative Updates [Freund-Schapire (1999)] 30

0 -sum games using Multiplicative Updates [Freund-Schapire (1999)] 31

Rewards instead of costs Maximize reward instead of minimizing cost.

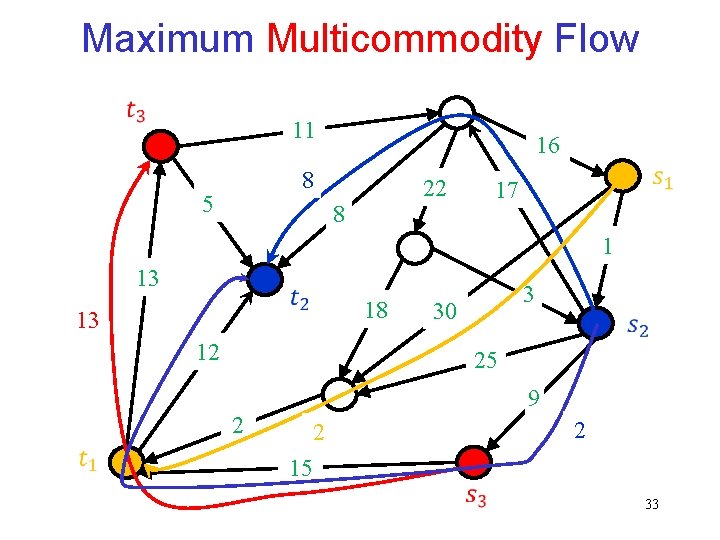
Maximum Multicommodity Flow 11 16 8 5 22 8 17 1 13 13 18 3 30 12 25 9 2 2 2 15 33

Maximum Multicommodity Flow Different commodities can share the edges of the network. The total flow on an edge should not exceed its capacity.

Maximum Multicommodity Flow We use a different LP formulation of the problem of possibly exponential size (!) 35

Maximum Multicommodity flow [Garg-Könemman (2007)] Our presentation follows [Arora-Hazan-Kale (2012)]. In each iteration:

Maximum Multicommodity flow [Garg-Könemman (2007)] (See next slide. )

Maximum Multicommodity flow [Garg-Könemman (2007)] 38

Maximum Multicommodity flow [Garg-Könemman (2007)] Maximum congestion Upon termination: 39

Maximum Multicommodity flow [Garg-Könemman (2007)] How many iterations are needed? Each iteration adds 1 to the congestion of at least one edge. 40

Positive Semidefinite Programming Can also be approximated using multiplicative updates. Interesting application: Approximation algorithm for MAX CUT

Bibliography Sanjeev Arora, Elad Hazan, Satyen Kale, The Multiplicative Weights Update Method: A Meta-Algorithm and Applications, Theory of Computing, Volume 8 (2012), pp. 121 -164 42

Bonus material Not covered in class this term “Careful. We don’t want to learn from this. ” (Calvin in Bill Watterson’s “Calvin and Hobbes”) 43

Packing Linear Programs Packing: 44

Packing Linear Programs “Simple” is used informally. The only requirement is that ORACLE can be efficiently implemented. 45

Packing Linear Programs The width. 46

Packing LPs using multiplicative weights [Plotkin-Shmoys-Tardos (1995)] Note: Satisfied constraints are more costly. If ORACLE returns “no” in any iteration, problem infeasible.

Packing LPs using multiplicative weights [Plotkin-Shmoys-Tardos (1995)]

Useful fact: 49

Packing LPs using multiplicative weights [Plotkin-Shmoys-Tardos (1995)]

Maximum Multicommodity Flow This is now a packing problem.

Maximum Multicommodity flow Otherwise, return “no”.

Maximum Multicommodity flow How good is the algorithm obtained using the framework? We also need to multiply by the cost of the binary search. The running time is not polynomial! 53