MS 101 Algorithms Instructor Neelima Gupta nguptacs du





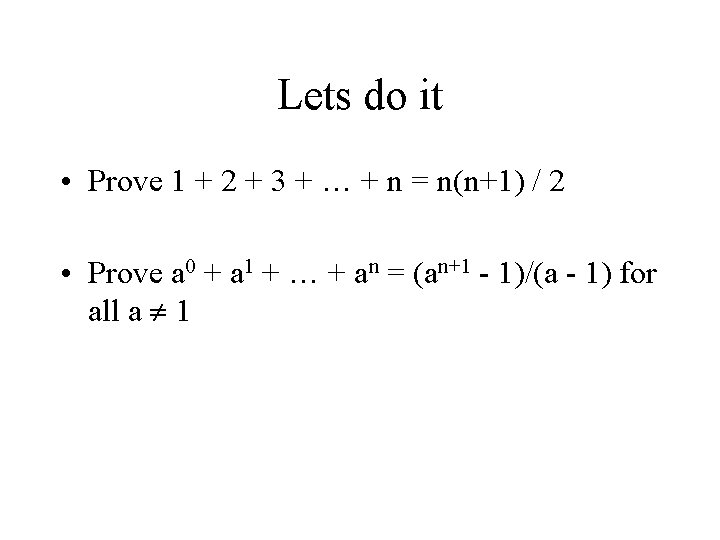

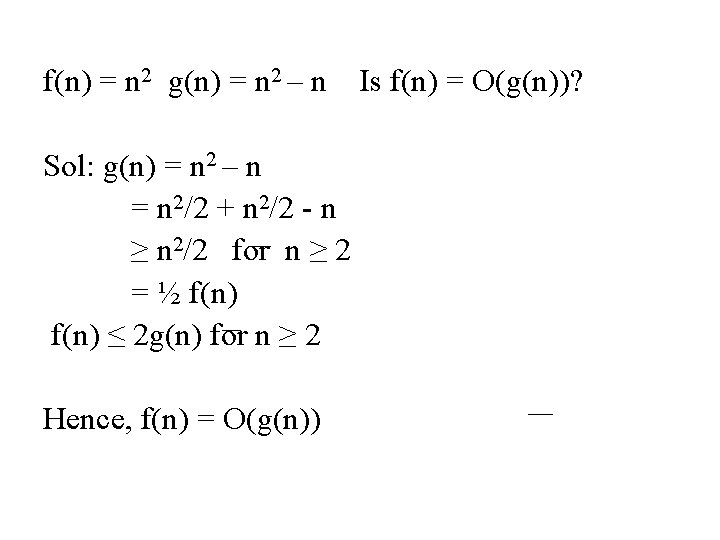
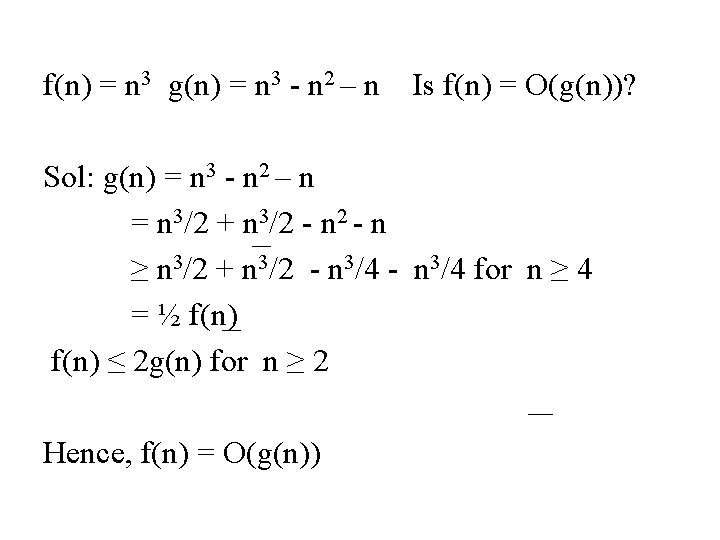
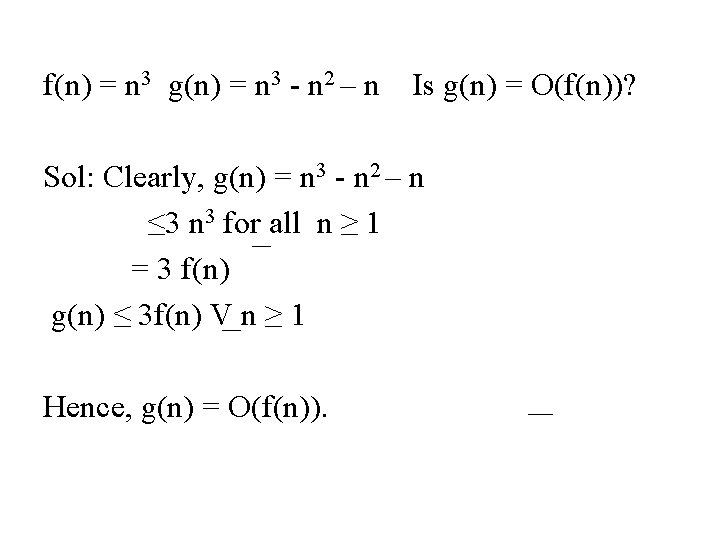

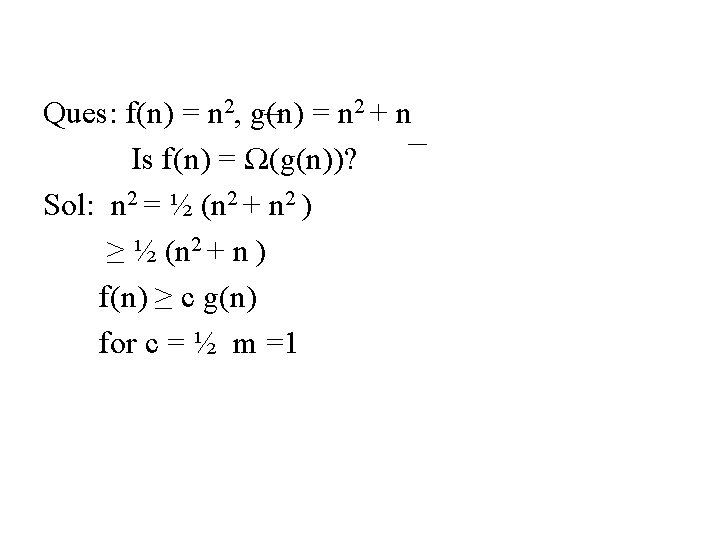
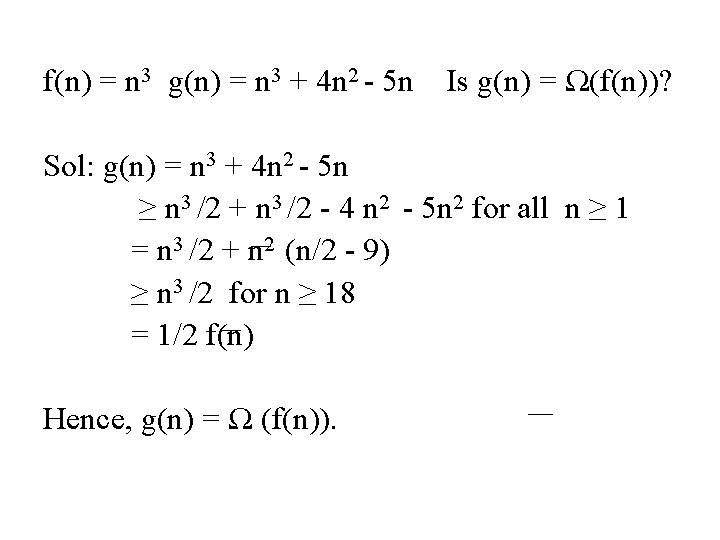















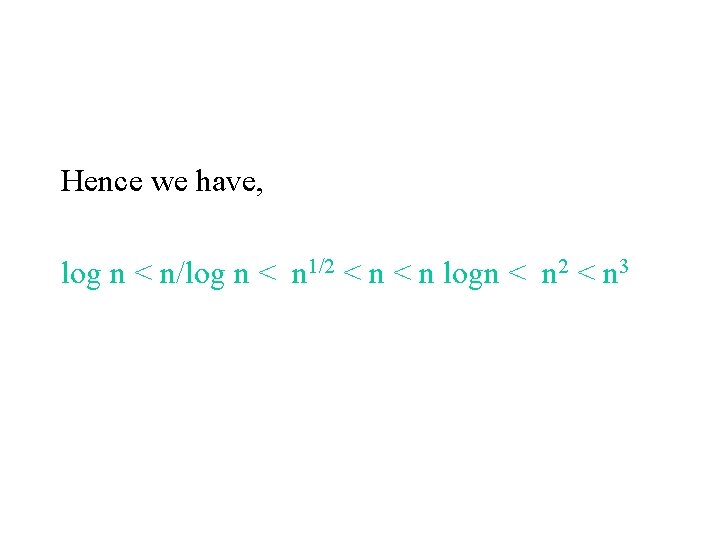












- Slides: 41

MS 101: Algorithms Instructor Neelima Gupta ngupta@cs. du. ac. in

Table Of Contents Mathematical Induction: Review Growth Functions

Review: Mathematical Induction • Suppose – S(k) is true for fixed constant k • Often k = 0 – S(n) S(n+1) for all n >= k • Then S(n) is true for all n >= k

Proof By Mathematical Induction • Claim: S(n) is true for all n >= k • Basis: – Show formula is true when n = k • Inductive hypothesis: – Assume formula is true for an arbitrary n • Step: – Show that formula is then true for n+1

Strong Induction • Strong induction also holds – Basis: show S(0) – Hypothesis: assume S(k) holds for arbitrary k <= n – Step: Show S(n+1) follows • Another variation: – Basis: show S(0), S(1) – Hypothesis: assume S(n) and S(n+1) are true – Step: show S(n+2) follows
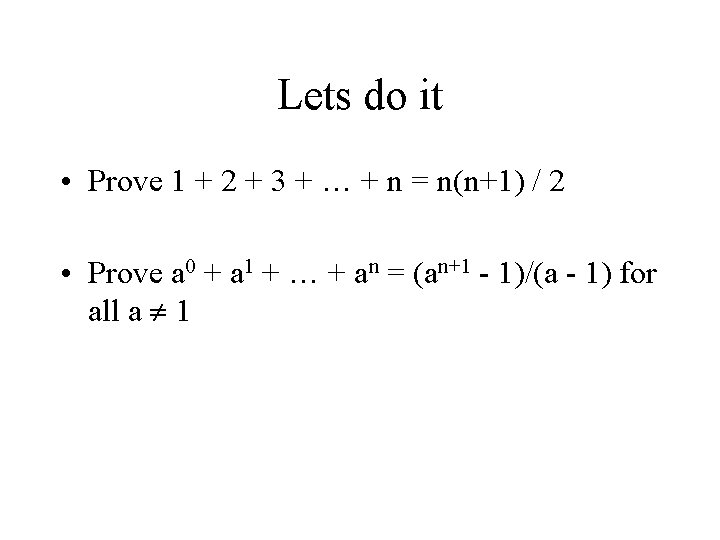
Lets do it • Prove 1 + 2 + 3 + … + n = n(n+1) / 2 • Prove a 0 + a 1 + … + an = (an+1 - 1)/(a - 1) for all a 1

Growth Functions • Big O Notation • In general a function – f(n) is O(g(n)) if there exist positive constants c and n 0 such that f(n) c g(n) for all n n 0 • Formally – O(g(n)) = { f(n): positive constants c and n 0 such that f(n) c g(n) n n 0 • Intuitively, it means f(n) grows no faster than g(n). • Examples: – n^2, n^2 – n^3, n^3 – n^2 – n
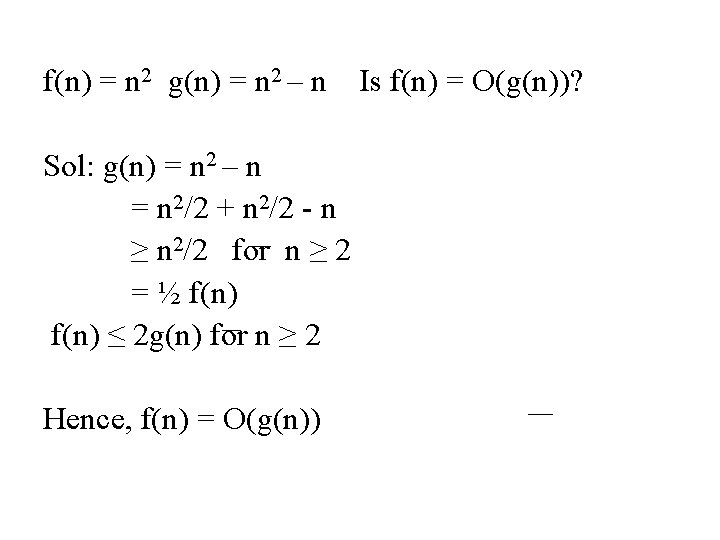
f(n) = n 2 g(n) = n 2 – n Sol: g(n) = n 2 – n = n 2/2 + n 2/2 - n ≥ n 2/2 for n ≥ 2 = ½ f(n) ≤ 2 g(n) for n ≥ 2 Hence, f(n) = O(g(n)) Is f(n) = O(g(n))?
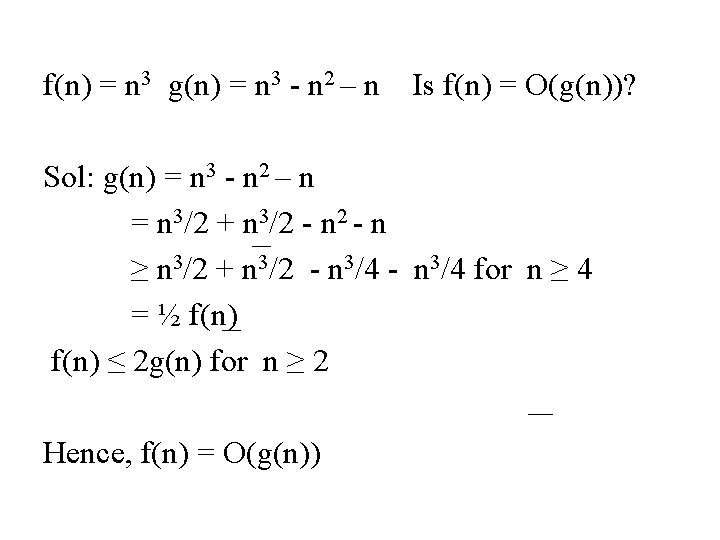
f(n) = n 3 g(n) = n 3 - n 2 – n Is f(n) = O(g(n))? Sol: g(n) = n 3 - n 2 – n = n 3/2 + n 3/2 - n ≥ n 3/2 + n 3/2 - n 3/4 for n ≥ 4 = ½ f(n) ≤ 2 g(n) for n ≥ 2 Hence, f(n) = O(g(n))
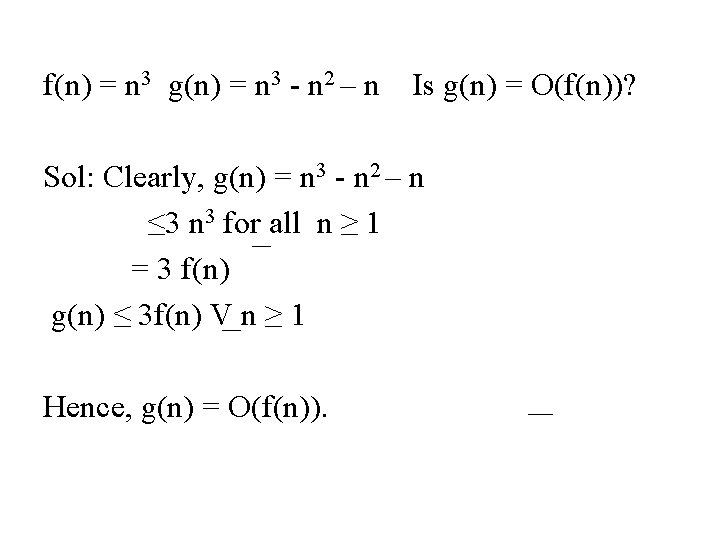
f(n) = n 3 g(n) = n 3 - n 2 – n Is g(n) = O(f(n))? Sol: Clearly, g(n) = n 3 - n 2 – n ≤ 3 n 3 for all n ≥ 1 = 3 f(n) g(n) ≤ 3 f(n) V n ≥ 1 Hence, g(n) = O(f(n)).

Omega Notation • In general a function – f(n) is (g(n)) if positive constants c and n 0 such that 0 c g(n) f(n) n n 0 Intuitively, it means f(n) grows at least as fast as g(n). • Examples: – n^2, n^2 + n – n^3, n^3 + n^2 – n
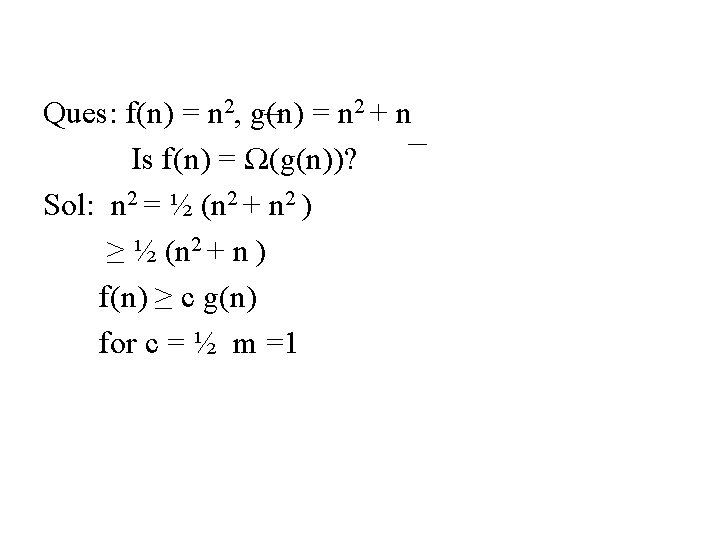
Ques: f(n) = n 2, g(n) = n 2 + n Is f(n) = Ω(g(n))? Sol: n 2 = ½ (n 2 + n 2 ) ≥ ½ (n 2 + n ) f(n) ≥ c g(n) for c = ½ m =1
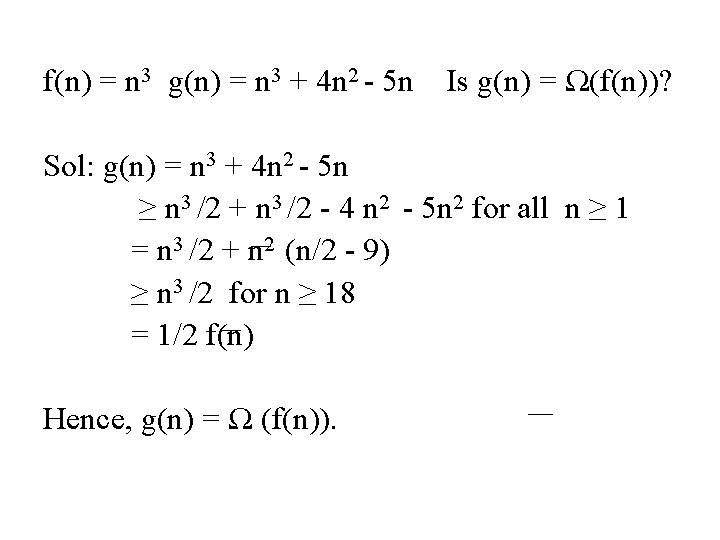
f(n) = n 3 g(n) = n 3 + 4 n 2 - 5 n Is g(n) = Ω(f(n))? Sol: g(n) = n 3 + 4 n 2 - 5 n ≥ n 3 /2 + n 3 /2 - 4 n 2 - 5 n 2 for all n ≥ 1 = n 3 /2 + n 2 (n/2 - 9) ≥ n 3 /2 for n ≥ 18 = 1/2 f(n) Hence, g(n) = Ω (f(n)).

Theta Notation • A function f(n) is (g(n)) if positive constants c 1, c 2, and n 0 such that c 1 g(n) f(n) c 2 g(n) n n 0

Relations Between , , O Theorem : For any two functions g(n) and f(n), f(n) = (g(n)) iff f(n) = O(g(n)) and f(n) = (g(n)). Proof: Simple. Do it.

Assignment No 1 Q 1 • Already proved a 0 + a 1 + … + an = (an+1 - 1)/(a - 1) for all a 1 – What is the sum for a = 2/3 as n infinity? Is it O(1)? Is it big or small? – For a = 2, is the sum = O(2^n)? Is it big or small? Q 2 • Show that a polynomial of degree k = theta(n^k).

Other Asymptotic Notations • A function f(n) is o(g(n)) if for every positive constant c, there exists a constant n 0 > 0 such that f(n) < c g(n) n n 0 • A function f(n) is (g(n)) if for every positive constant c, there exists a constant n 0 > 0 such that c g(n) < f(n) n n 0 • Intuitively, – () is like > – () is like = – o() is like < – () is like – O() is like

Arrange some functions • f(n) = O(g(n)) => f(n) = o(g(n)) ? • Is the converse true? • Let us arrange the following functions in ascending order (assume log n = o(n) is known) – n, n^2, n^3, sqrt(n), n^epsilon, log^2 n, n log n, n/log n, 2^n, 3^n

Relation between n & 2 n Solution: let c > 0 be any constant such that n < c n 2 i. e. 1 < c n i. e. n > 1 / c Hence n < c n 2 for n > 1 / c i. e. n = o( n 2) we can also write it as n < n 2.

Relation between 2 n & 3 n Solution: let c> 0 be any constant such that n 2 < c n 3 Þ 1<cn Þ n>1/c Hence n 2 < c n 3 " n > 1 / c i. e. n 2 = o( n 3) we can also write it as n 2 < n 3. Combining the previous result we can write n < n 2 < n 3

Relation between n & 1/2 n Solution: let c> 0 be any constant such that n 1/2 < c n i. e n < c 2 n 2 i. e 1 < c 2 n i. e n > 1/ c 2 i. e. n 1/2 < c n for n > 1/c 2 i. e. n 2 = o( n 3) we can also write it as n 1/2 < n. Combining the previous result n 1/2 < n 3

Relation between n & log n • For the time being we can assume the result log ( n ) = o(n) Þ log ( n ) < n we will prove it later.

Relation between n 1/2 & log n Assume log n = o(n) let c > 0 be any constant for c/2 > 0 there exists m > 0 such that log n < (c/2) n for n > m changing variables from n to n 1/2 we get log(n 1/2 ) < (c/2) n 1/2 for n 1/2 > m ½ log( n ) < (c/2) n 1/2 for n > m 2

Contd. . let m 2 = k log( n ) < c n 1/2 for n > k Since c > 0 was chosen arbitrarily hence log n = o( n 1/2 ) or log n < n 1/2 Combining the results we get log n < n 1/2 < n 3

Relation between 2 n & nlog n • Since log n = o(n) for c > 0, n 0 > 0 such that n n 0, we have log n < c n Multiplying by n on both sides we get n log( n ) < c n 2 n n 0 Þ nlog n = o( n 2 ) Þ nlog n < n 2

Relation between n & nlog n Solution: let c> 0 be any constant such that n < c n log (n) Þ 1 < c log( n ) Þ log( n) > 1 / c Þ n > e 1/c i. e. n < c n log n n > e 1/c Since c was chosen arbitrarily n = o( n log n ) or n < n log n Combining the results we can get log n < n 1/2 < n logn < n 2 < n 3

Relation between n & n/log n • We know that n = o(nlogn) for c > 0, n 0 > 0 such that n n 0, we have n < c n log n dividing both sides by log n we get n/ log( n) < c n n n 0 Þ n / logn = o(n) i. e. n / logn < n

Assignment No 2 • Show that log^M n = o(n^epsilon) for all constants M>0 and epsilon > 0. Assume that log n = o(n). Also prove the following Corollary: log n = o(n/log n) • Show that n^epsilon = o(n/logn ) for every 0 < epsilon < 1.
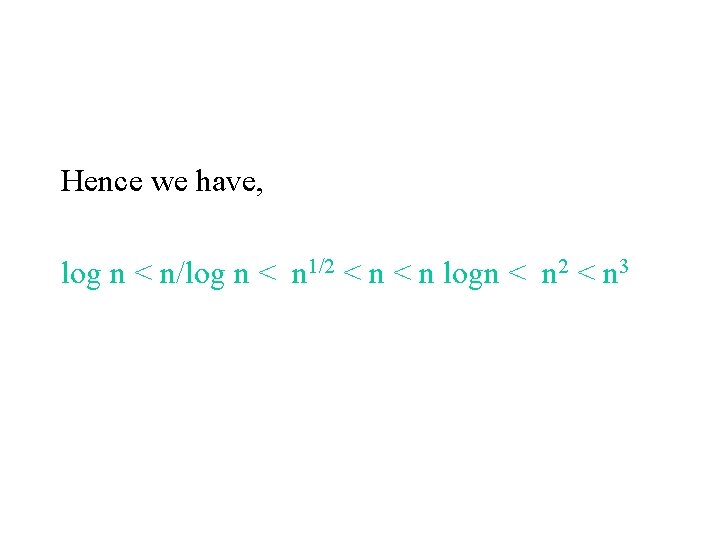
Hence we have, log n < n/log n < n 1/2 < n logn < n 2 < n 3

Assignment No 3 • Show that – lim f(n)/g(n) = 0 => f(n) = o(g(n)). n→∞ – lim f(n)/g(n) = c => f(n) = θ(g(n)). n → ∞, where c is a positive constant. • Show that log n = o(n). • Show that n^k = o(2^n) for every positive constant k.

• Show by definition of ‘small o’ that a^n = o(b^n) whenever a < b , a and b are positive constants. Hence we have, log n < n/log n < n 1/2 < n logn < n 2 < n 3 <2 n < 3 n

Why the constants ‘c’ and ‘m’? • Suppose we have two algorithms to solve the problem say sorting: Insertion Sort and Merge sort for eg. • Why should we have more than one algorithm to solve the same problem? • Ans: efficiency. • What’s the measure of efficiency? • Ans: System resources for example ‘time’. • How do we measure time?

Contd. . • • IS(n) = O(n^2) MS(n) = O(nlog n) MS(n) is faster than IS(n). Suppose we run IS on a fast machine and MS on a slow machine and measure the time (since they were developed by two different people living in different part of the globe), we may get less time for IS and more for MS…wrong analysis • Solution: count the number of steps on a generic computational model

Computational Model: Analysis of Algorithms • Analysis is performed with respect to a computational model • We will usually use a generic uniprocessor random -access machine (RAM) – All memory equally expensive to access – No concurrent operations – All reasonable instructions take unit time • Except, of course, function calls – Constant word size • Unless we are explicitly manipulating bits

Running Time • Number of primitive steps that are executed – Except for time of executing a function call, in this model most statements roughly require the same amount of time • y=m*x+b • c = 5 / 9 * (t - 32 ) • z = f(x) + g(y) • We can be more exact if need be

But why ‘c’ and ‘m’? • Because – We compare two algorithms on the basis of their number of steps and – the actual time taken by an algorithm is ‘c’ times the number of steps.

Why ‘m’? • We need efficient algorithms and computational tools to solve problems on big data. For example, it is not very difficult to sort a pack of 52 cards manually. However, to sort all the books in a library on their accession number might be tedious if done manually. • So we want to compare algorithms for large input.

An Example: Insertion Sort Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

Assignment 4 • Show that Insertion Sort takes O(n^2) steps by counting each and every step. – Is it O(n)? – Is it O(n^3)?

Lower Bound Notation • We say Insertion. Sort’s run time is (n) • Proof: – Suppose run time is an + b • Assume a and b are positive (what if b is negative? ) – an + b

Up Next • Solving recurrences – Substitution method – Master theorem
 Neelima gupta delhi university
Neelima gupta delhi university Neelima balakrishnan
Neelima balakrishnan Brahmi
Brahmi Tcole 1014 basic instructor course
Tcole 1014 basic instructor course Instructor vs teacher
Instructor vs teacher Basic instructor course #1014
Basic instructor course #1014 Cbrf instructor registry
Cbrf instructor registry Catia instructor
Catia instructor Basic instructor course texas
Basic instructor course texas Basic instructor course texas
Basic instructor course texas Forced perspective room
Forced perspective room Tcole advanced instructor course
Tcole advanced instructor course Usmc jrotc vacancies
Usmc jrotc vacancies Cisco certified instructor
Cisco certified instructor Nfpa 1403
Nfpa 1403 Tipos de participantes en una capacitación
Tipos de participantes en una capacitación Delmar cengage learning instructor resources
Delmar cengage learning instructor resources Nra certified instructor logo
Nra certified instructor logo Drawing and painting the virtual instructor
Drawing and painting the virtual instructor Instructor
Instructor Pepperball launcher nomenclature
Pepperball launcher nomenclature Acr medical term
Acr medical term Nrp instructor toolkit
Nrp instructor toolkit Tp 12863
Tp 12863 Mptc firearms
Mptc firearms Basic instructor course tcole
Basic instructor course tcole Instructor office hours
Instructor office hours Naismith was an instructor of
Naismith was an instructor of Tcole advanced instructor course
Tcole advanced instructor course Instructor responsibilities and professionalism
Instructor responsibilities and professionalism Neither of my two suitcases is adequate for this trip
Neither of my two suitcases is adequate for this trip Basic instructor course #1014
Basic instructor course #1014 Cisco instructor certification
Cisco instructor certification Instructor operating station
Instructor operating station Basic instructor course texas
Basic instructor course texas Basic instructor course texas
Basic instructor course texas Jrotc marksmanship instructor course online
Jrotc marksmanship instructor course online Please clean your room
Please clean your room Amit gupta microsoft
Amit gupta microsoft Aarti gupta md
Aarti gupta md Odu linux servers
Odu linux servers Projection bias
Projection bias
































































