MS 101 Algorithms Instructor Neelima Gupta nguptacs du

MS 101: Algorithms Instructor Neelima Gupta ngupta@cs. du. ac. in

Network Flows Edited by Divya Gaur(39, MCS '09) Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09)

DOMAIN Depict flow of a material (liquid, gas, current) from source to sink. Source: Material generator. Sink: Final destination to receive material. Flow: Rate of flow of material. Conduit: Medium for material transfer (pipe, wires). Capacity: Maximum rate at which material can flow through conduit. Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

Goal To solve the Maximum Flow problem Compute greatest rate at which material can flow from source to sink subject to specified constraints. Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

TECHNIQUE Flow Network • A directed graph depicting source, conduit, sink modeling the flow. • Each directed edge represents conduit. • Vertices are conduit conjunctions through which material flows but does not collect. • At a vertex , Rate of inflow = rate of outflow. Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

NOTATIONS AND CONSTRAINTS Flow Network : G(V, E) Edge : (u, v) є E Capacity of edge: c(u, v) ≥ 0 If (u, v) does not belong to E the c(u, v) = 0 Source: s Sink: t Graph connected ie. |E| ≥|V| - 1 Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

Flow in G a real valued function f: V X V → R satisfying constraints: Capacity Constraint: For all u, v є V, f(u, v) ≤ c(u, v) Flow from one vertex to another must not exceed given capacity. Skew Symmetry: For all u, v є V, f(u, v) = -f(v, u) Flow from a vertex u to a vertex is the negative of the flow in the reverse direction. Flow Conservation: For all u є V- {s, t} Σf(u, v) = 0 vєV Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

f(u, v) : Flow from u to v. It can be either positive , negative or zero. Value of flow |f| =Σf(u, v) = 0 : Total flow out of source. vєV Total flow out of a vertex V ≠ u, v =0 By Skew symmetry Σf(u, v) = 0 uєV for all v є V- {s, t} ie. . total flow into vertex =0. Total net flow at a vertex : Total positive flow leaving a vertex – Total positive flow entering a vertex. So by Flow Conservation property total net flow at a vertex =0 Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

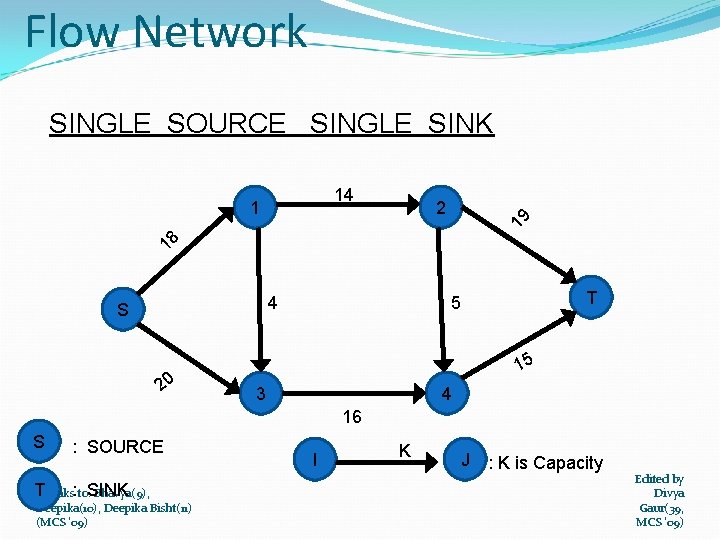
Flow Network SINGLE SOURCE SINGLE SINK 14 2 19 1 18 4 S 20 T 5 15 3 4 16 S : SOURCE TThanks: to: SINK Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) I K J : K is Capacity Edited by Divya Gaur(39, MCS '09)

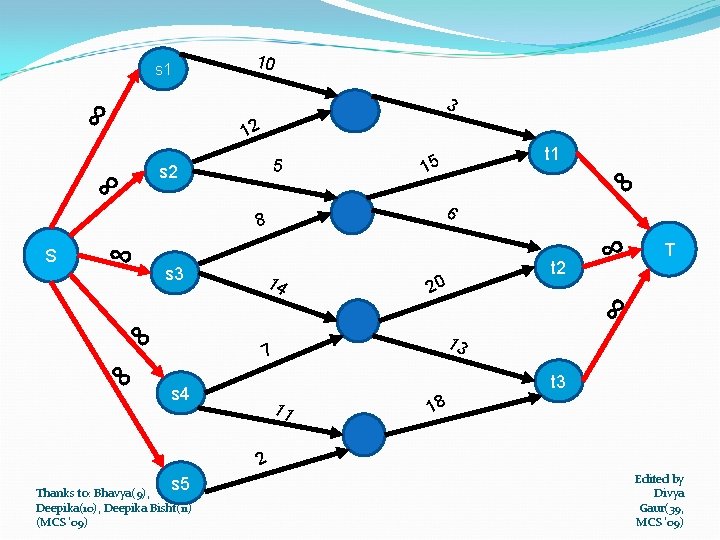
MULTIPLE SOURCE MULTIPLE SINK 10 s 1 3 12 5 s 2 8 s 3 14 7 s 4 11 2 s 5 Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) 15 t 1 6 20 13 18 t 2 t 3 Edited by Divya Gaur(39, MCS '09)

To solve multiple source multiple sink problem Add a supersource s and directed edge (s, si) with c(s, si) = ∞ for each i=1, 2, …. , m Add a supersink t and directed edge (ti, t) with c(ti, t) = ∞ for each i =1, 2, …. , n Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

10 s 1 ∞ 3 12 ∞ 6 8 s 3 14 20 t 2 ∞ T ∞ S s 2 t 1 15 ∞ ∞ 5 ∞ 7 13 ∞ t 3 s 4 11 18 2 s 5 Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

Ford Fulkerson Method Instructor: Ms Neelima Gupta Edited by Divya Gaur(39, MCS '09) Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09)

Ford_Fulkerson(G, s, t) 1. initialize flow f to 0 2. while there exists augmenting path p 3. do augment f along p 4. return f Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

RESIDUAL NETWORK RESIDUAL CAPACITY OF (u, v) cf The amount of additional flow that can be pushed from u to v before exceeding c(u, v). cf = c(u, v) – f(u, v) Eg : - c(u, v)=10, f(u, v)=5 then flow can be increased by 5 units ie. . residual capacity = 5. RESIDUAL NETWORK OF G INDUCED BY f , Gf Gf =(V, Ef) where Ef= {(u, v) є V X V: cf(u, v) > 0 } ie. Each edge of the residual network or residual edge can Edited by admit flow > 0. Divya Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Gaur(39, MCS '09)

AUGMENTING PATHS AUGMENTING PATH ( P) Path from s to t in residual network Gf. The augmenting path admits additional positive flow from u to v within capacity constraint. The maximum amount by which flow can be increased on each edge in P is residual capacity of P, cf = min{cf (u, v): (u, v) is on P}. Example: if cf (u, v)=3 then the flow through each edge of p can be increased by 3 without violating capacity constraint. Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

ALGORITHM FORD_FULKERSON(G, s, t) 1. for each edge (u, v) є E[G] 2. do f[u, v]← 0 3. f[v, u]← 0 4. while there exists a path from s to t in Gf 5. do cf (p)←min{c(u, v) : (u, v) is in p} 6. for each edge (u, v) in p 7. do f[u, v]← f[u, v] + cf (p) 8. f[u, v]← - f[u, v] Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

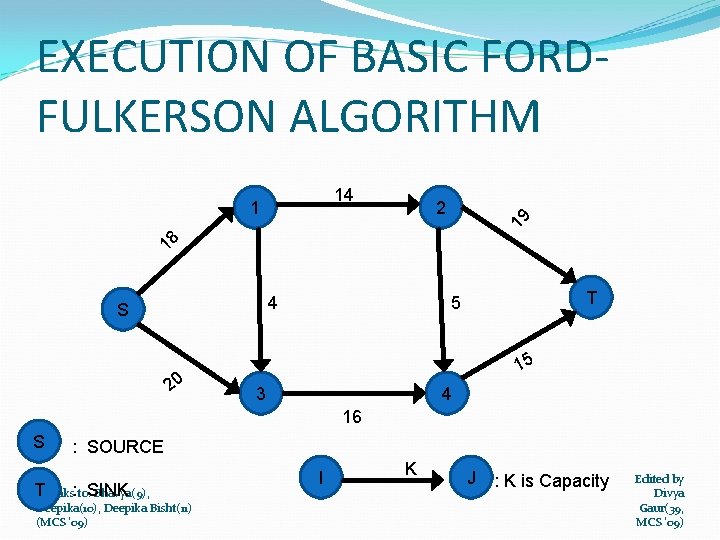
DESCRIPTION OF ALGORITHM 1 -3 initialise flow f to 0. 4 -8 finds augmenting path p in residual network and augments flow f along p by residual capacity cf (p). When no augmenting path exists flow f is maximum. Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

EXECUTION OF BASIC FORDFULKERSON ALGORITHM 14 2 19 1 18 4 S 20 T 5 15 3 4 16 S : SOURCE TThanks: to: SINK Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) I K J : K is Capacity Edited by Divya Gaur(39, MCS '09)

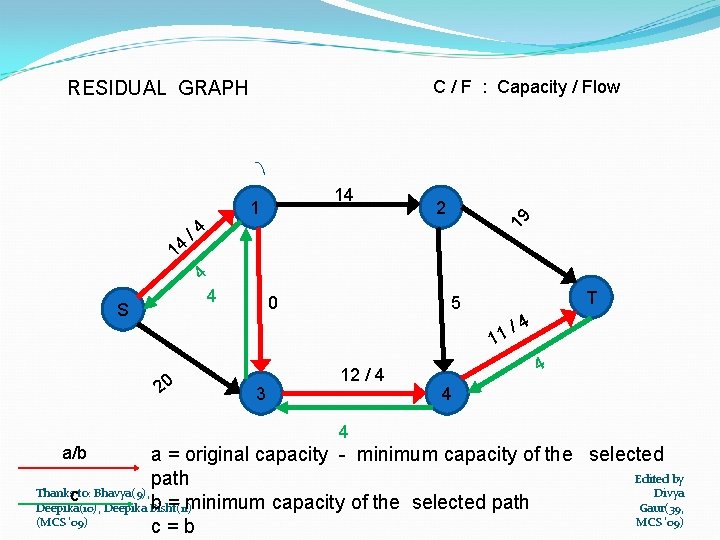
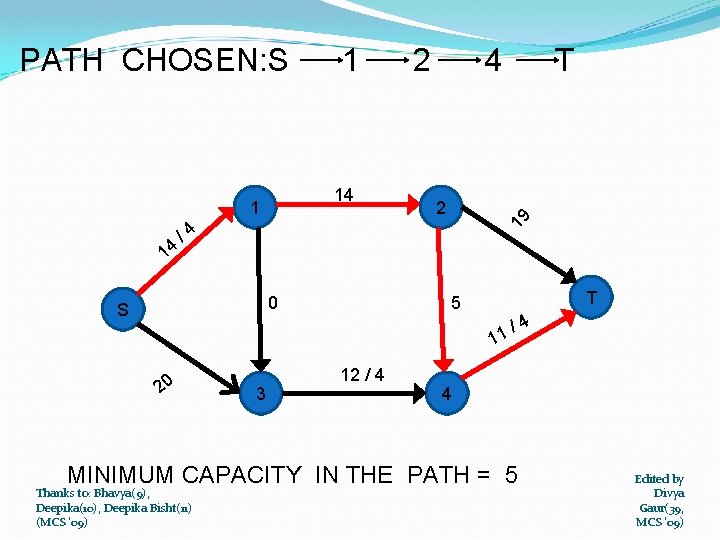
1 3 4 14 1 T 2 19 PATH CHOSEN : S 18 4 S 20 T 5 15 3 4 16 MINIMUM CAPACITY IN THE PATH = 4 Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

C / F : Capacity / Flow 14 /4 4 4 S 14 1 0 2 19 RESIDUAL GRAPH T 5 / 11 20 3 12 / 4 4 4 a/b a = original capacity - minimum capacity of the selected Edited by path Divya Thankscto: Bhavya(9), b = minimum capacity of the selected path Gaur(39, Deepika(10), Deepika Bisht(11) (MCS '09) c=b

14 1 2 4 2 /4 0 S T 19 PATH CHOSEN: S T 5 / 11 20 3 12 / 4 4 MINIMUM CAPACITY IN THE PATH = 5 Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) 4 Edited by Divya Gaur(39, MCS '09)

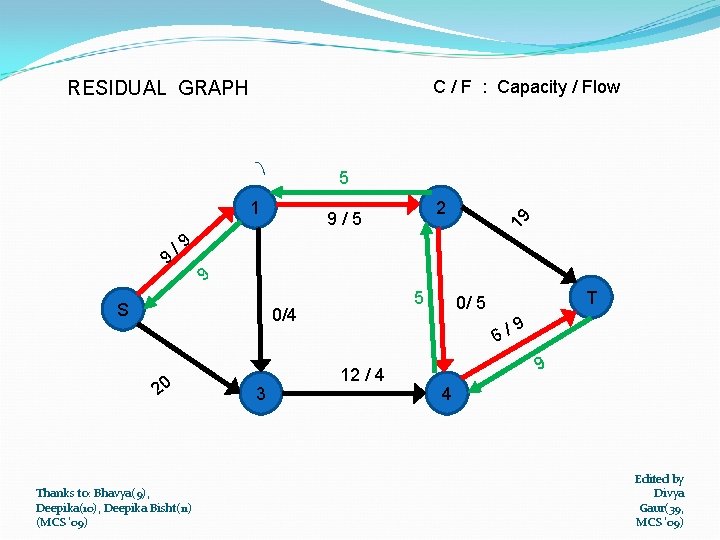
C / F : Capacity / Flow RESIDUAL GRAPH 5 9 2 9/5 19 1 /9 9 S 5 0/4 20 Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) 3 T 0/ 5 6/ 12 / 4 9 9 4 Edited by Divya Gaur(39, MCS '09)

1 9 1 9/5 2 T 2 19 PATH CHOSEN : S /9 0/4 S T 0/ 5 6/ 20 3 12 / 4 9 4 MINIMUM CAPACITY IN THE PATH = 9 Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

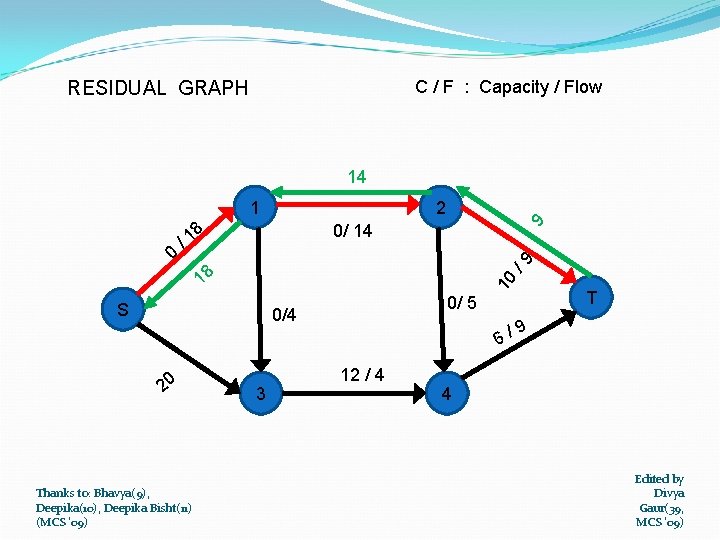
C / F : Capacity / Flow RESIDUAL GRAPH 14 1 8 1 / /9 18 S Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) 3 T 0/ 5 0/4 20 9 0/ 14 10 0 2 6/ 12 / 4 9 4 Edited by Divya Gaur(39, MCS '09)

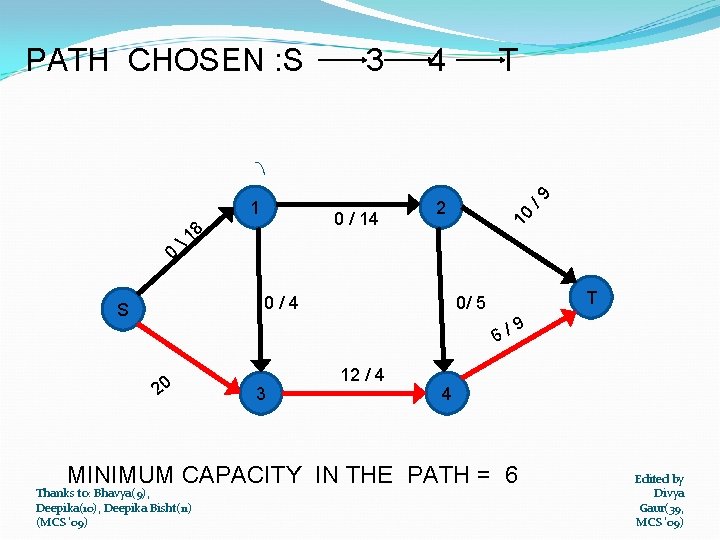
0 0 / 14 8 1 4 2 0/4 S T /9 1 3 10 PATH CHOSEN : S T 0/ 5 6/ 20 3 12 / 4 9 4 MINIMUM CAPACITY IN THE PATH = 6 Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

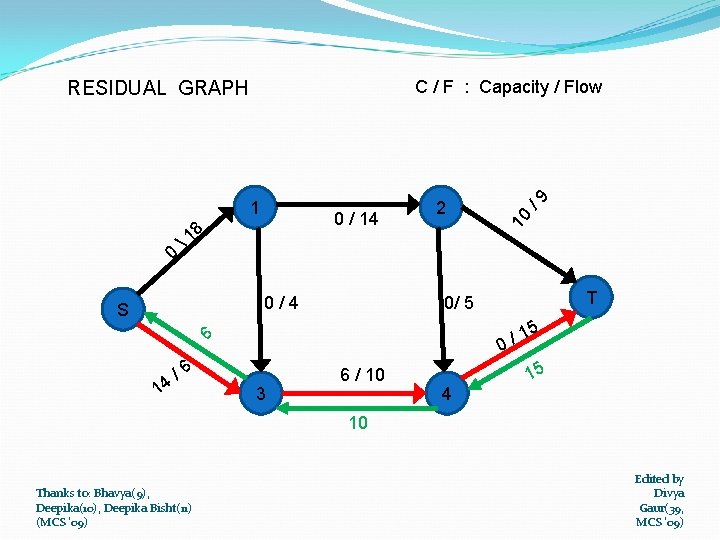
0 0 / 14 8 1 0/4 S 2 14 T 0/ 5 5 1 / 0 6 /6 10 1 /9 C / F : Capacity / Flow RESIDUAL GRAPH 3 6 / 10 4 15 10 Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

1 5 0/4 S 2 0 / 14 8 0 4 2 T /9 1 3 10 PATH CHOSEN: S (BACKTRACKING) T 0/ 5 5 14 1 / 0 /6 3 6 / 10 4 MINIMUM CAPACITY IN THE PATH = 5 Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

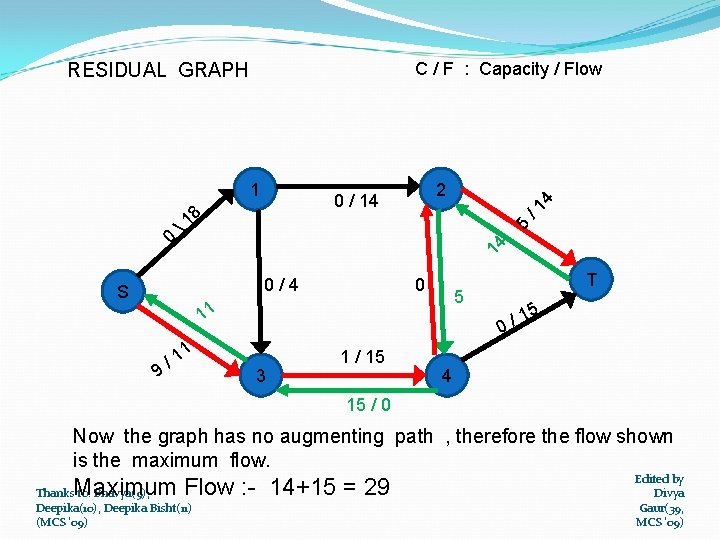
C / F : Capacity / Flow 1 /1 5 8 1 14 0 2 0 / 14 0/4 S 0 5 11 1 9 4 RESIDUAL GRAPH /1 3 1 / 15 T 5 1 0/ 4 15 / 0 Now the graph has no augmenting path , therefore the flow shown is the maximum flow. Flow : - 14+15 = 29 Thanks. Maximum to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

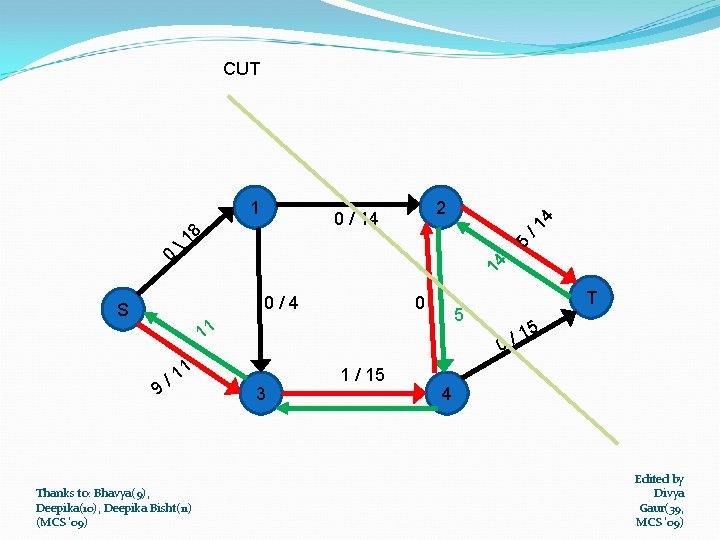
CUTS OF FLOW NETWORK Flow is maximum iff its residual network has no augmenting path. CUT(s, t) OF FLOW NETWORK G : A partition of V into S and T=V - S such that s є S and t є T. It is a collection of edges separating the network into S and T. If f is flow , then the net flow across the cut is f(S, T) and capacity is c(S, T). A minimum cut of network is cut with minimum capacity over all cuts of the network. Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

CUT 14 5 1 /1 8 0 2 0 / 14 0/4 S 0 5 11 1 9 4 1 /1 Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) 3 1 / 15 T 5 1 / 0 4 Edited by Divya Gaur(39, MCS '09)

OPTIMALITY MAX FLOW MIN CUT THEOREM 1. f is maximum flow in G 2. Gf contains no augmenting paths 3. |f| = c(S, T) for some cut(S, T) of G If the flow f* reported by the algorithm is optimal then there exists a cut C* on which residual capacity of cut = 0. The initial capacity of C* must have been f* and must have been utilised completely and hence residual capacity = 0. C* is a minimum cut since if another cut’s capacity is less than C*’s then it would not be possible to send f* flow. Optimality is achieved since otherwise some augmenting path would be present with capacity at least one. Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

ANALYSIS OF THE ALGORITHM Running time of the algorithm is O(f* X time to compute augmenting path). 1 -3 take O(E) time. While loop is executed at most |f*| times since flow value increases by at least one unit in each iteration. Time to compute an augmenting path using BFS or DFS is O(E). Each iteration of the while loop hence takes O(E) time. Hence total running time of FORD FULKERSON is O(E |f*|). Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

A DEEPER SIGHT INTO ANALYSIS f* can be very big as it depends on capacities. f* could be as big as Σc(u, v). Since it depends on the values of capacities so it is not polynomial in input size which is Σlog ci + E + V where ci’s could be large. Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

Running Time depends on how the augmenting path p is determined. If capacities are small and |f*| is small running time is good. Example illustrates effect on time with large |f*|. Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

Here max flow = 400. But if the first augmenting path is s->v 1 ->v 2 ->t, flow would be one and then choosing s-> v 2 -> v 1 - >t in even numbered iterations and s->u->v->t in odd ones increases flow by just one in each iteration(total of 400 iterations) and perform a total of 400 augmentations. Thanks to: Bhavya(9), Deepika(10), Deepika Bisht(11) (MCS '09) Edited by Divya Gaur(39, MCS '09)

Edmonds-Karp Algorithm Thanks to: Swati Vohra (29, MCS '09)

Edmonds Karp Algorithm u s t v Choose the shortest augmenting path from s to t in residual network. Path is shortest in terms of no. of edges. Critical edge : - minimum weight edge of an augmenting path. Thanks to: Swati Vohra (29, MCS '09)

Notations Initial graph : - G Flow in G form s to u: f Residual graph : Gf $f(u, v) : - shortest path distance from u to v in Gf Flow in residual graph : f 1 (computed as shortest path over Gf ) Thanks to: Swati Vohra (29, MCS '09)

f 1 s f u u v As f is the shortest distance from s to u so f <= f 1 and $f(s, u) <= $f 1(s, u) V u. Thanks to: Swati Vohra (29, MCS '09) t

Critical Edge s u v t If (u, v) is critical edge along augmenting path then : $f(s, v) = $f(s, u) +1 (edge) $f(s, v) in Gf increases monotonically with each flow augmentation. Once the flow is augmented, edge (u, v) disappears from the Gf. Thanks to: Swati Vohra (29, MCS '09)

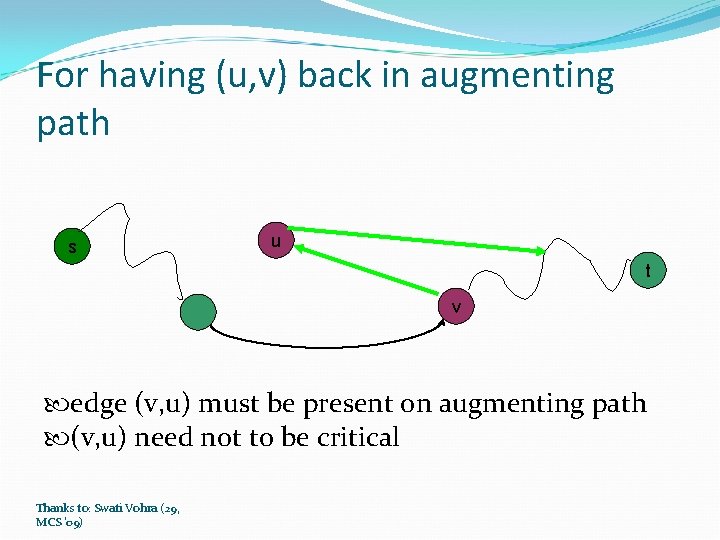
When (u, v) is not present in augmenting path s u t v Thanks to: Swati Vohra (29, MCS '09)

For having (u, v) back in augmenting path s u t v edge (v, u) must be present on augmenting path (v, u) need not to be critical Thanks to: Swati Vohra (29, MCS '09)

So, $f 1(s, u) = $f 1(s, v) +1 & $f(s, v) = $f(s, u) +1 $f(s, v) <= $f 1(s, v) Therefore, $f 1(s, u) = $f 1(s, v) +1 >=($ f(s, v) +1) = $ f(s, u) +2 Thanks to: Swati Vohra (29, MCS '09)

Analysis In a critical edge (u, v) , Distance of u from s initially is at least 0. Every time (u, v) edge becomes critical again distance of u from s increased by at least 2. Intermediate vertices on shortest path from s to u can’t contain s, u, t. (since (u, v) on the critical path means s != t). So until u becomes unreachable from s its distance is at most IVI-2. So every (u, v) edge can become critical at most (IVI-2)/2 times. Thanks to: Swati Vohra (29, MCS '09)

Pair of vertices that can have edge in Gf = O(E) Each edge can become critical O(V) time. Total no. of critical edges = O(VE). Each iteration of Ford Fulkerson can be implemented in O(E) time when augmenting path is found by BFS so total running time of Edmonds Karp= O(VE^2). Thanks to: Swati Vohra (29, MCS '09)

Maximum bipartite matching Thanks to: Geetanjali Shivas (13, MCS '09)

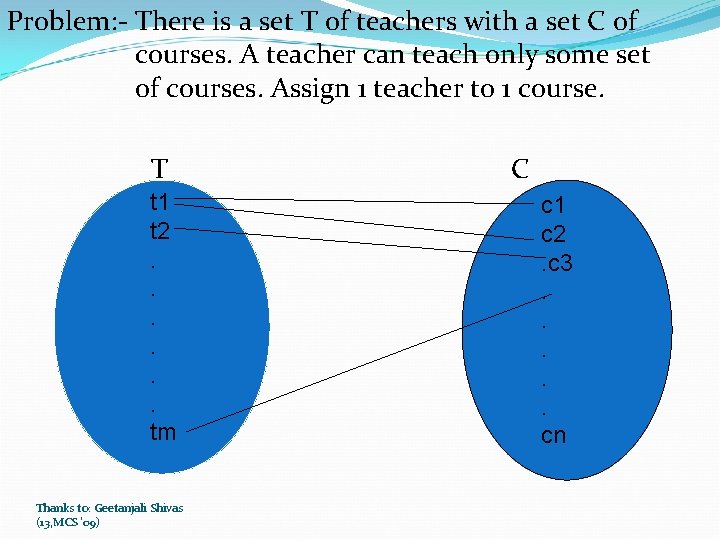
Problem: - There is a set T of teachers with a set C of courses. A teacher can teach only some set of courses. Assign 1 teacher to 1 course. T t 1 t 2. . . tm Thanks to: Geetanjali Shivas (13, MCS '09) C c 1 c 2. c 3. . . cn

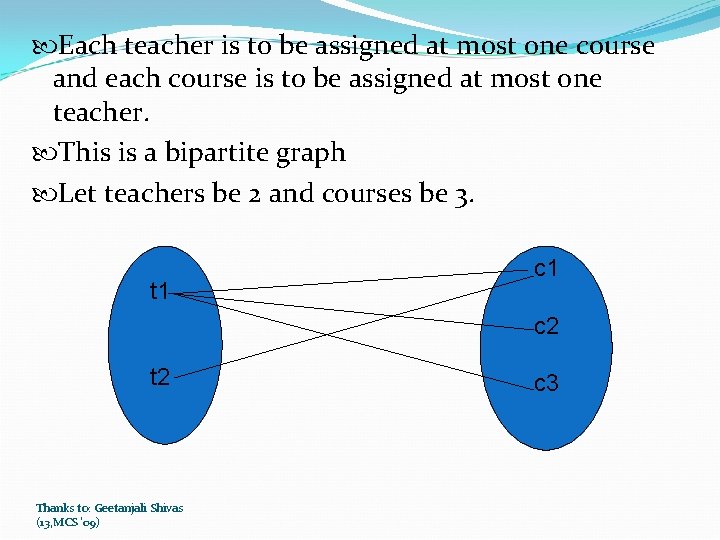
Each teacher is to be assigned at most one course and each course is to be assigned at most one teacher. This is a bipartite graph Let teachers be 2 and courses be 3. t 1 c 2 t 2 Thanks to: Geetanjali Shivas (13, MCS '09) c 3

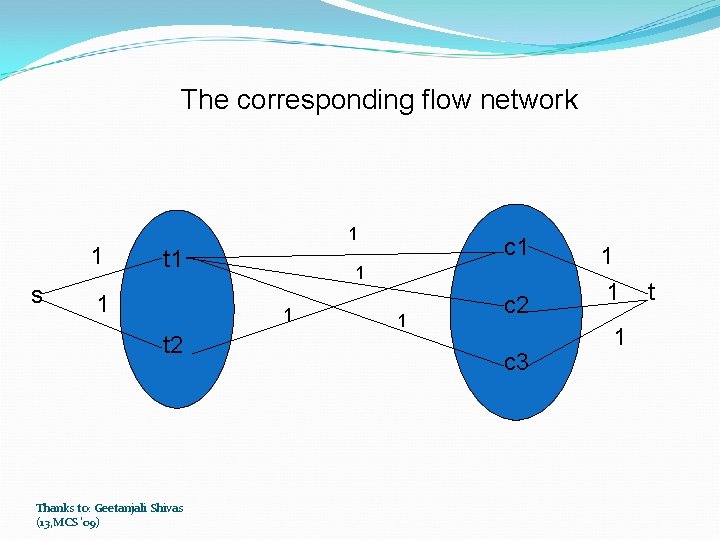
Convert the problem into flow network problem in which flows corresponds to matchings. Let source s and sink t be new vertices. Draw an edge from source s to each vertices in T and from each vertices in C to sink t. Capacity of each edge from s to T, T to C, C to t is 1. 1 t In the end, each unit of flow will be equivalent to a match between a teacher and a course, so each edge will be assigned a capacity of 1. Thanks to: Geetanjali Shivas (13, MCS '09)

The corresponding flow network 1 s 1 t 1 1 t 2 Thanks to: Geetanjali Shivas (13, MCS '09) c 1 1 c 2 c 3 1 1 1 t

Now if we assign t 1 to c 1, then t 2 will not get any course and c 2, c 3 are also not assigned to any teachers. Therefore we select a subset E’ of edges such that no two edges resides on same vertex. We want to find the maximum edges. Q: - Why capacity from s to T cannot be taken more than 1? Ans: - If capacity from s to T is more than 1 then any vertex in T would be selected more than 1 time and matched more than once. Thanks to: Geetanjali Shivas (13, MCS '09)

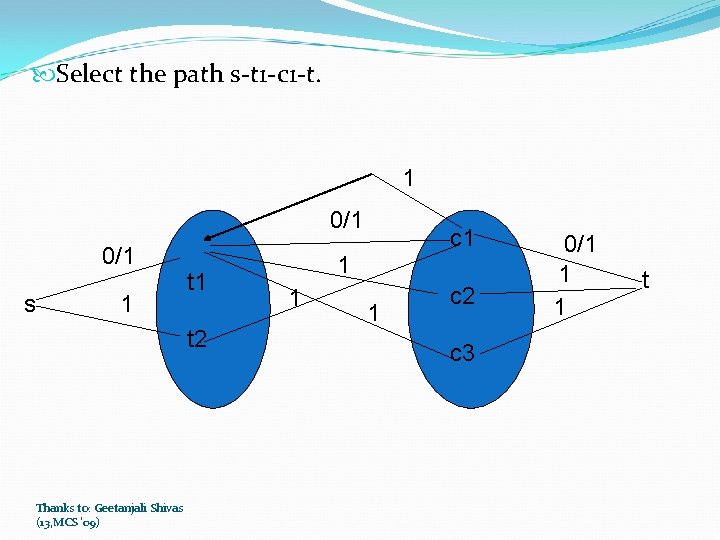
Select the path s-t 1 -c 1 -t. 1 0/1 s 1 t 2 Thanks to: Geetanjali Shivas (13, MCS '09) c 1 1 c 2 c 3 0/1 1 1 t

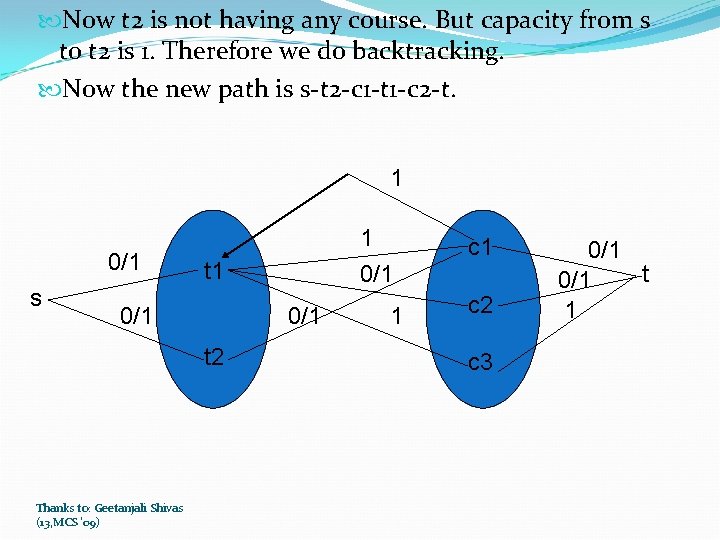
Now t 2 is not having any course. But capacity from s to t 2 is 1. Therefore we do backtracking. Now the new path is s-t 2 -c 1 -t 1 -c 2 -t. 1 0/1 s t 1 0/1 t 2 Thanks to: Geetanjali Shivas (13, MCS '09) 1 0/1 1 c 2 c 3 0/1 t 0/1 1

Now t 2 is assigned c 1 and t 1 is assigned to c 2. Flow from t 1 to c 2 is 1, t 2 to c 1 is 1. But residual capacity from t 1 to c 2 is 0 and t 2 to c 1 is 0. Total network flow is 2. Therefore teacher t 1 is matched with course c 2 and teacher t 2 is matched with course c 1. Thanks to: Geetanjali Shivas (13, MCS '09)