Model Checking An introduction overview Gordon J Pace

Model Checking: An introduction & overview Gordon J. Pace December 2002

History of Formal Methods n n n Automata model of computation: mathematical definition but intractable. Formal semantics: more abstract models but proofs difficult, tedious and error prone. Theorem proving: proofs rigorously checked but suffers from ‘only Ph. Ds need apply’ syndrome.

The 1990 s Radiation therapy machine overdoses patients, n Pentium FDIV bug, n Ariane-V crash. n Industry willing to invest in algorithmic based, push-button verification tools.

Model-Checking Identify an interesting computation model, n For which the verification question is decidable, n And tractable on interesting problems. n Write a program to answer verification questions. n

Formal Semantics n Operational Semantics: (v: =n, s) ( , s[v n]) (P, s) ( , s’) (P; Q, s) (Q, s’)

Formal Semantics n Denotational Semantics of Timed Systems: v V’ 0 [[ delay (v’, v) ]] def = v’(t+1)=v(t) / v’(0)=low

Transition Systems Q, , I Q = States n = Transition relation ( Q x Q) n I = Initial states ( Q) n

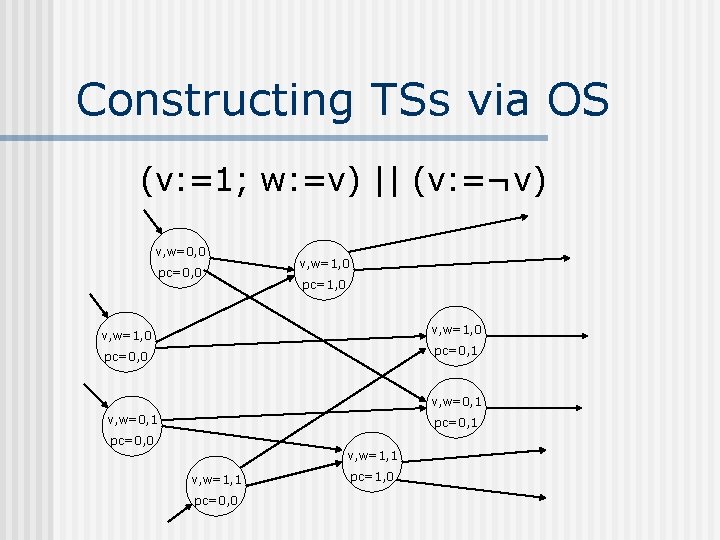
Constructing TSs via OS (v: =1; w: =v) || (v: =¬v) v, w=0, 0 pc=0, 0 v, w=1, 0 pc=1, 0 v, w=1, 0 pc=0, 1 v, w=0, 1 pc=0, 0 v, w=1, 1 pc=0, 0 pc=1, 0

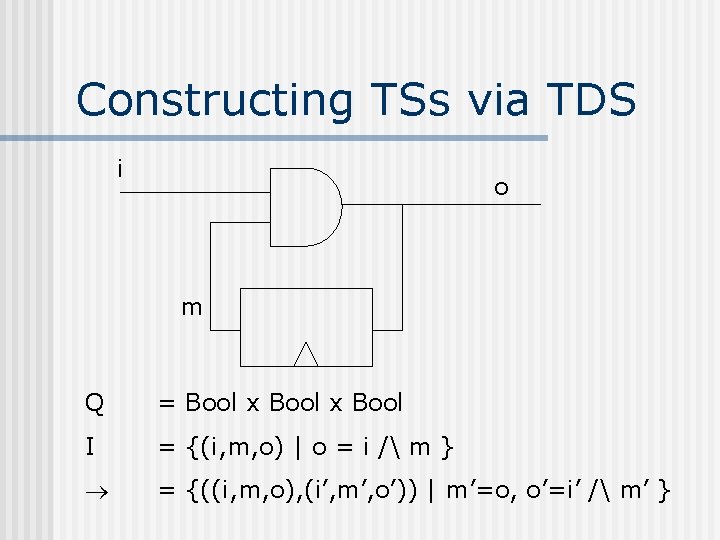
Constructing TSs via TDS i o m Q = Bool x Bool I = {(i, m, o) | o = i / m } = {((i, m, o), (i’, m’, o’)) | m’=o, o’=i’ / m’ }

Note: n We will be ‘constructing’ TSs from a symbolic (textual/graphical) description of the system. This is a step which explodes exponentially (linear increase in description may imply exponential increase in statespace size).

Properties of TSs Safety properties: ‘Bad things never happen’. eg The green lights on a street will never be on at the same time as the green lights on an intersecting street. n Liveness properties: ‘Good things eventually happen’. eg A system will never request a service infinitely often without eventually getting it. n

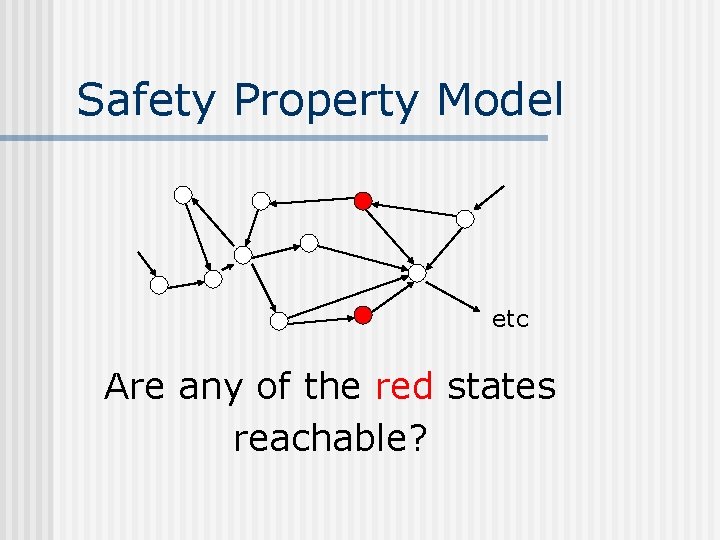
Safety Property Model etc Are any of the red states reachable?

Safety Property Model Given a transition system M= Q, , I and a set of ‘bad’ states B, are there any states in B which are reachable in M?

A Reachability Algorithm R 0 = I Rn+1 = Rn (Rn) where: (P) = { s’ | s P: s s’ } Reachable set is the fix-point of this sequence. Termination and correctness are easy to prove.

A Reachability Algorithm R : = I; Rprev : = ; while (R Rprev) do Rprev : = R; R : = R (R); if (B R ) then BUG; CORRECT;

State Space Representation n Explicit representation Keeping a list of traversed states. n State-explosion problem. n Looking at the recursion stack will give counter-example (if one is found). n Breath-first search guarantees a shortest counter-example. n

Typical Optimizations n On-the-fly exploration: Explore only the ‘interesting’ part of the tree (wrt property and graph). Example: Construct graph only at verification time. Finding a bug would lead to only partial unfolding of the description into a transition system.

Typical Optimizations Partial order reduction: By identifying commuting actions (ones which do not disable each other), we can ignore parts of the model. Example: To check for deadlock in (a!; P b!; Q), we may just fire actions a and b in this order rather than take all interleavings. n

Typical Optimizations n Compositional verification: Build TS bottom up, minimising the automata as one goes along. Example: To construct (P Q), construct P and minimise to get P’, construct Q and minimise to get Q’, and then calculate (P’ Q’).

Typical Optimizations n Interface-Based Verification: Use information about future interfaces composands while constructing subcomponents. Example: Constructing the full rhs of (10 c; P + 5 c; Q + …) Huge (5 c; Tea) gives a lot of useless branches which the last process never uses.

State Space Representation n R : = I; Rprev : = ; Symbolic state representation: while (R Rprev) do Use a symbolic Rprev : = R; R : = R (R); formula to if (B R ) then BUG; represent the set of states. CORRECT; Requires: representation of empty set, union, intersection, relation application, and set equality test.

Symbolic Representation Use boolean formulae Let v 1 to vn be the boolean variables in the state space. A boolean formula f(v 1, …, vn) represents the set of all states (assignments of the variables) which satisfy the formula.

Symbolic Representation Double the variables To represent the transition relation, give a formula over variables v 1, …, vn and v’ 1, …, v’n relating the values before and after the step.

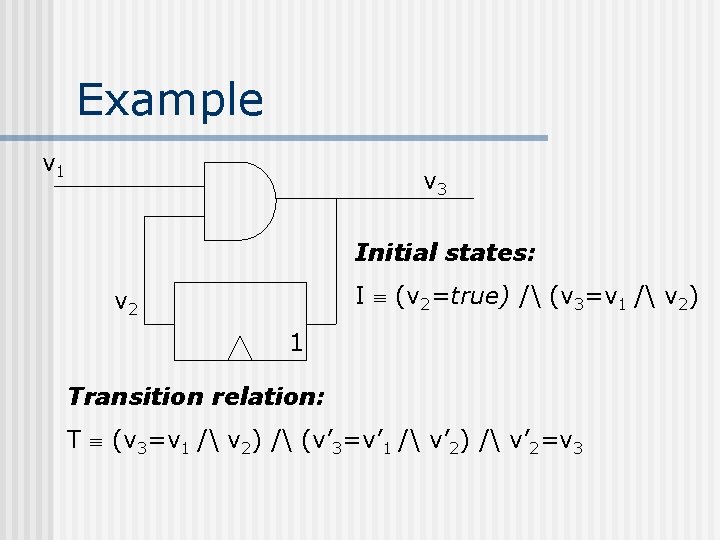
Example v 1 v 3 Initial states: I (v 2=true) / (v 3=v 1 / v 2) v 2 1 Transition relation: T (v 3=v 1 / v 2) / (v’ 3=v’ 1 / v’ 2) / v’ 2=v 3

Set Operators: Empty set: = false Intersection: P Q = P / Q Union: P Q = P / Q Transition relation application: (P) = ( vars: P / T)[vars’/vars] Testing set equality: P=Q iff P Q

The Problem Calculating whether a boolean formula is a tautology is an NPcomplete problem. n In practice representations like Binary Decision Diagrams (BDDs) and algorithms used in SAT checkers perform quite well on typical problems. n

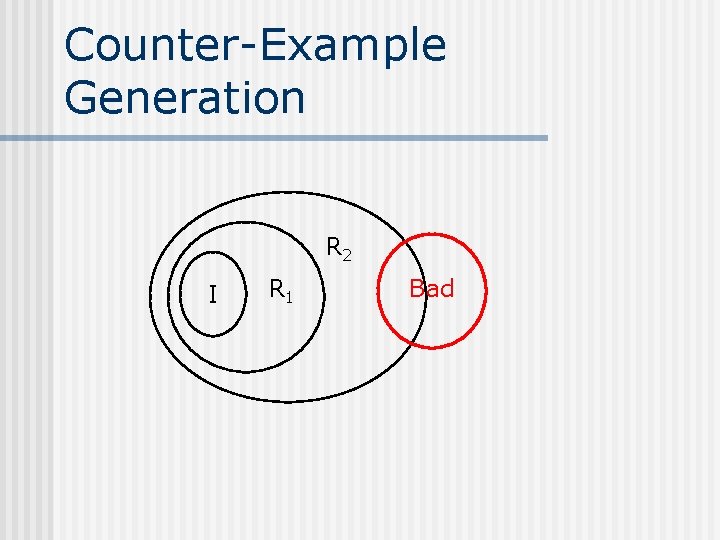
Counter-Example Generation I=R 0 Bad

Counter-Example Generation I R 1 Bad

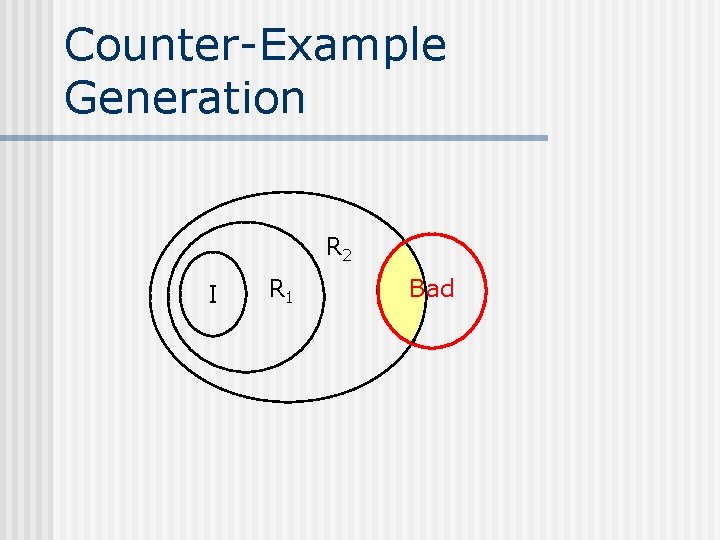
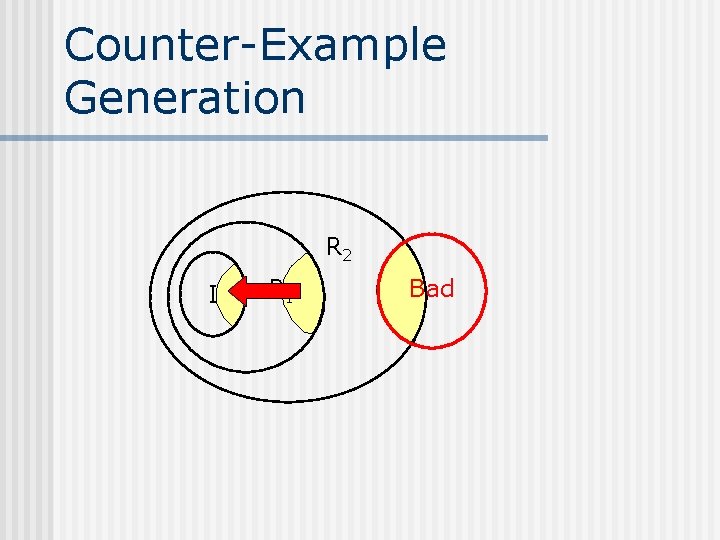
Counter-Example Generation R 2 I R 1 Bad

Counter-Example Generation R 2 I R 1 Bad

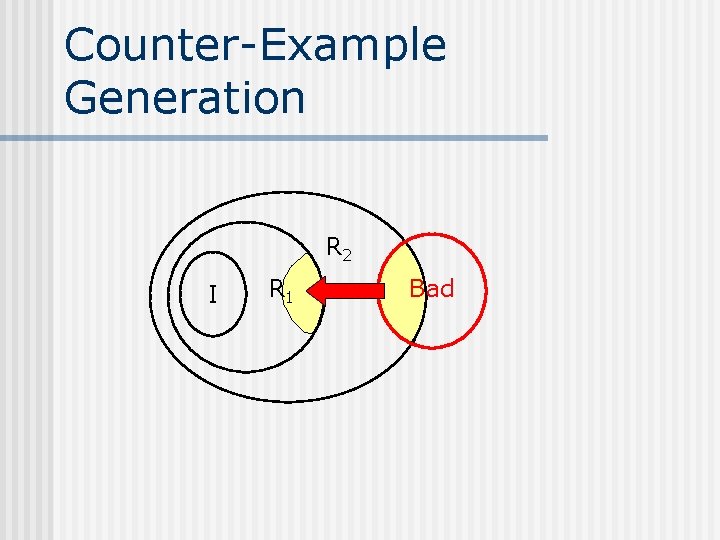
Counter-Example Generation R 2 I R 1 Bad

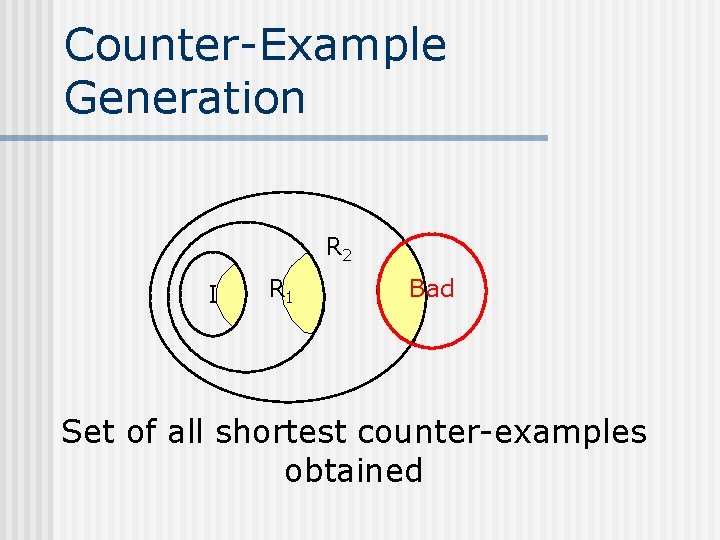
Counter-Example Generation R 2 I R 1 Bad

Counter-Example Generation R 2 I R 1 Bad Set of all shortest counter-examples obtained

Abstract Interpretation Technique to reduce state space to explore, transition relation to use. n Collapse state space by approximating wrt property being verified. n Can be used to verify infinite state systems. n

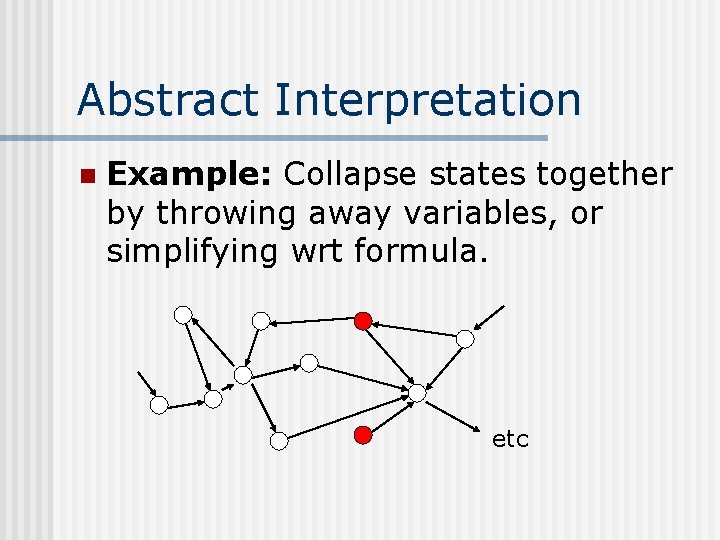
Abstract Interpretation n Example: Collapse states together by throwing away variables, or simplifying wrt formula. etc

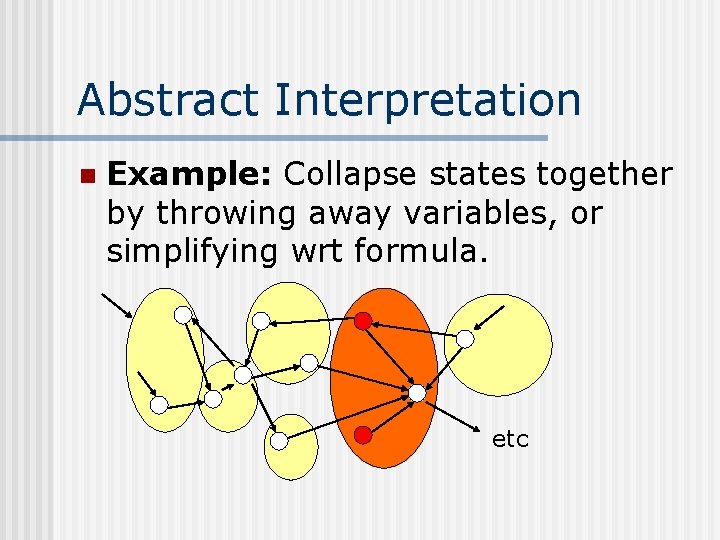
Abstract Interpretation n Example: Collapse states together by throwing away variables, or simplifying wrt formula. etc

Abstract Interpretation n Example: Collapse states together by throwing away variables, or simplifying wrt formula. etc

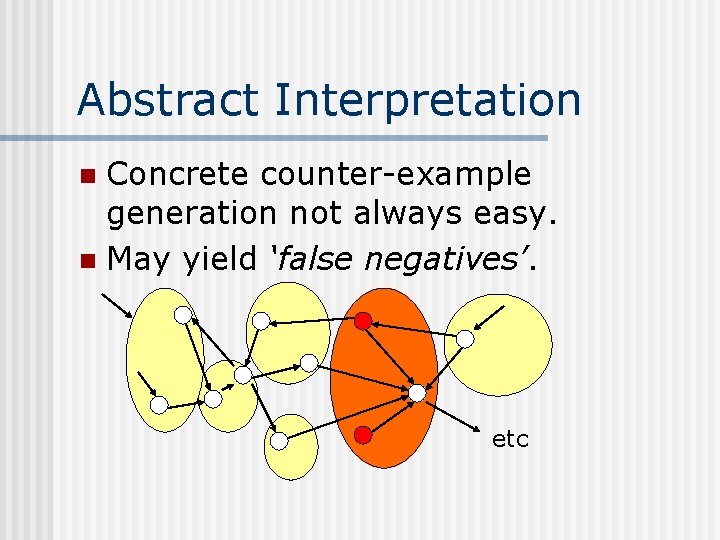
Abstract Interpretation Concrete counter-example generation not always easy. n May yield ‘false negatives’. n etc

Other Techniques n Backward Analysis R 0 = Bad Rn+1 = Rn -1(Rn) If R be the fix-point of this sequence, the system is correct iff R I = .

Other Techniques n Induction (depth 1): If … 1. The initial states are good, and Any good state can only go to a good state, then 2. The system is correct.

Other Techniques Induction (depth n): If … 1. Any chain of length n starting from an initial state yields only good states, and 2. Any chain of n good states can only be extended to reach a good state, then, The system is correct. n

Other Techniques n Induction By starting with n=1 and increasing, (plus adding some other constraints) we get a complete TS verification technique.

State-of-the-art n n Explicit state traversal: No more than 107 generated states. Works well for interleaving, asynchronous systems. Symbolic state traversal: Can reach up to 10150 (overall) states. Works well for synchronous systems. n n Sometimes may work with thousands of variables … With abstraction, 101500 states and above have been reported!

State-of-the-art Combined with other techniques, microprocessor producers are managing to ‘verify’ large chunks of their processors. n Application of model-checking techniques on real-life systems still requires expert users. n

Tools n n Various commercial and academic tools available. Symbolic: n n BDD based: SMV, Nu. SMV, VIS, Lustre tools. Sat based: Prover tools, Chaff, Hugo, Bandera toolset. n Explicit state: CADP, Spin, CRL, Edinburgh n Various high-level input languages: Workbench, FDR. Verilog, VHDL, LOTOS, CSP, CCS, C, JAVA.

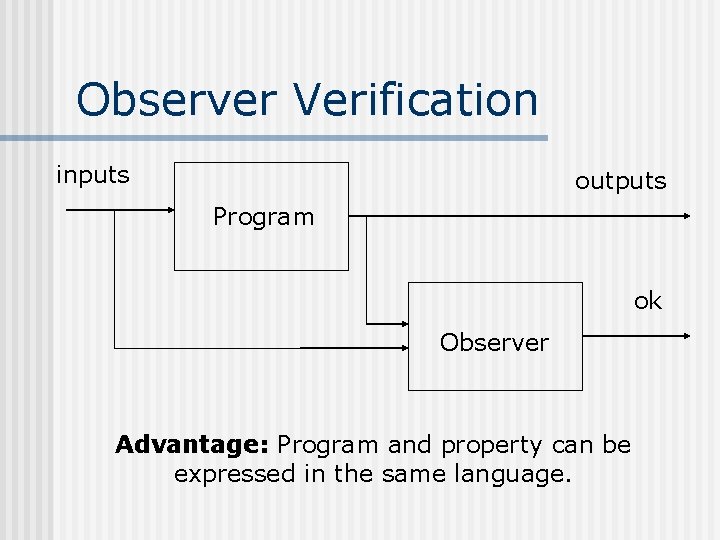
Stating Properties n Safety properties are easy to specify Intuition: ‘no bad things happen’. n If you can express a new output variable ok which is false when something bad happens, then this your property is a safety property (observer based verification). n Not all properties are safety properties. n

Observer Verification inputs outputs Program ok Observer Advantage: Program and property can be expressed in the same language.

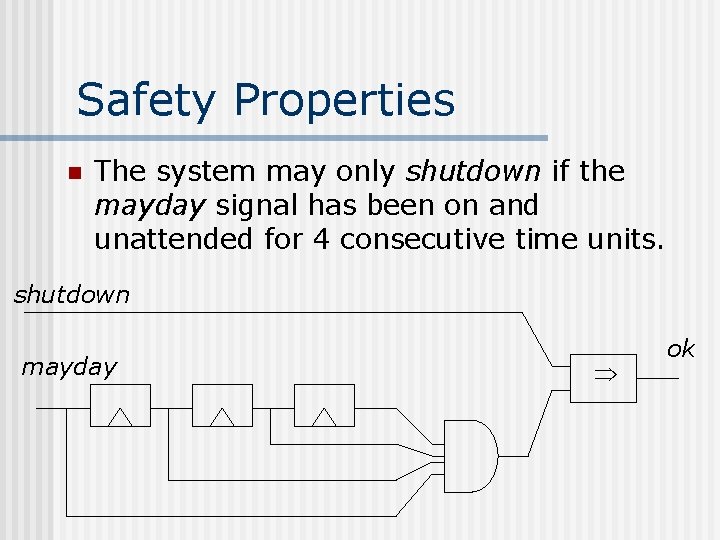
Safety Properties n The system may only shutdown if the mayday signal has been on and unattended for 4 consecutive time units. shutdown mayday ok

Non-Safety Properties Bisimulation based verification n Temporal logic based verification n Linear time logic (eg LTL) Globally (Finally bell) n Branching time logic (eg CTL) AG (ding EF dong) n Globally (Globally req Finally ack)

Beyond Finite Systems Example: Induction on structure: From: Prog(in, out) satisfies Prop(in, out) Prog(in, m) / Prop(m, out) satisfies Prop(in, out) Conclude: Any chain of Prog’s satisfies Prop. n

Philosophical Issues So does this constitute a proof? n Can I now claim my product to be correct? n Would a proof that P=NP change verification as we now know it? n

What I would have also liked to talk about … n n n Other techniques (STE, BMC, …), More about infinite systems, Testing and combining testing with verification, Interaction between theorem-provers and model-checkers, Model-checking other types of systems (hybrid systems, Petri-Nets, etc).

What now? Potential projects … Verification of Kevin & co’s synchronisation algorithms, n Use grammar induction to improve interface based verification, n SPee. DI and hybrid system verification, n Structural induction to model-check compiler properties. n