Men Activar HE con Ejemplos y Ejercicios Propiedades

Menú Activar HE con Ejemplos y Ejercicios Propiedades exponenciales. Propiedades logarítmicas. Solución de ecuaciones logarítmicas. Gráficas de funciones exponenciales. Gráficas de funciones logarítmicas. Resumen del capítulo. © Manuel Pontigo Alvarado. ISBN 978 -9968 -9634 -2 -8 Instituto Tecnológico de Costa Rica.

Propiedades Exponenciales: Multiplicación La multiplicación de los exponentes está definida por: Considere: x = 6 ; a = 2 b; = 4 Fórmula a operar: La instrucción para la HE es Resuelto mediante la HE =6^6 Respuesta: 2 6; 4; =6^6 R: Elija cualquier juego de numerales para x, a y b diferentes a los usados y resuelva. 2

Propiedades Exponenciales: División caso 1 La división de los exponentes está definida por: Considere: x = 6; a = 6 b; = 4. Fórmula a operar: Instrucción para la He: =(6^6)/(6^4) R: Elija cualquier juego de numerales para x, a y b diferentes a los usados y resuelva. 3

Propiedades Exponenciales: División caso 2 La división de los exponentes está definida por: Considere: x = 6; a = 6 b; = -4. Fórmula a operar: Instrucción para la He: =(6^6)/(6^-4) R: Elija cualquier juego de numerales para x, a y b diferentes a los usados y resuelva. 4

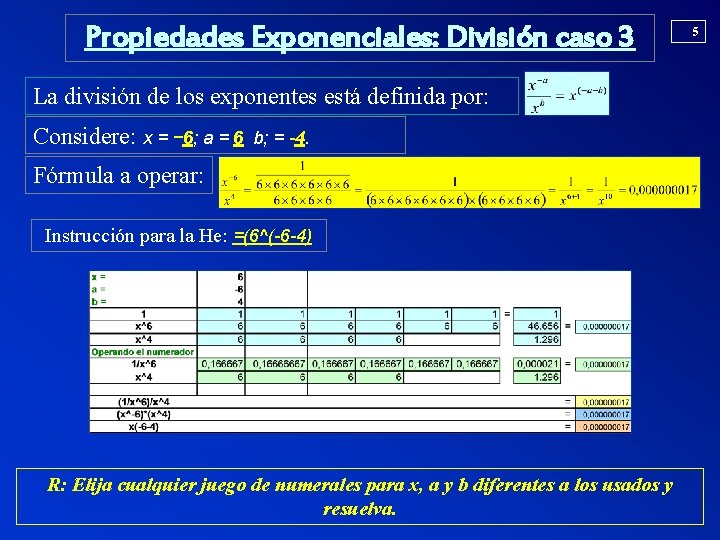
Propiedades Exponenciales: División caso 3 La división de los exponentes está definida por: Considere: x = − 6; a = 6 b; = -4. Fórmula a operar: Instrucción para la He: =(6^(-6 -4) R: Elija cualquier juego de numerales para x, a y b diferentes a los usados y resuelva. 5

Propiedades Exponenciales: Distributiva de la multiplicación. La distribución de la multiplicación en los exponentes está definida por: Considere; x = 5; y = 4; a = 3 Formula a operar: Instrucción para la He: =(5 4)^3 ó 5^3 4^3 ó =(B 115*B 116)^B 117 R: Elija cualquier juego de numerales para x, a y b diferentes a los usados y resuelva. 6

Propiedades Exponenciales: Distribución de la división. La distribución de la división en los exponentes está definida por: Considere; x = 5; y = 4; a = 3 Fórmula a operar: R: Elija cualquier juego de numerales para x, a y b diferentes a los usados y resuelva. 7

Propiedades Exponenciales: La potencia de una potencia en los exponentes está definida por: Considere; x = 5; y = 4; a = 3 Fórmula a operar: R: Elija cualquier juego de numerales para x, a y b diferentes a los usados y resuelva. 8

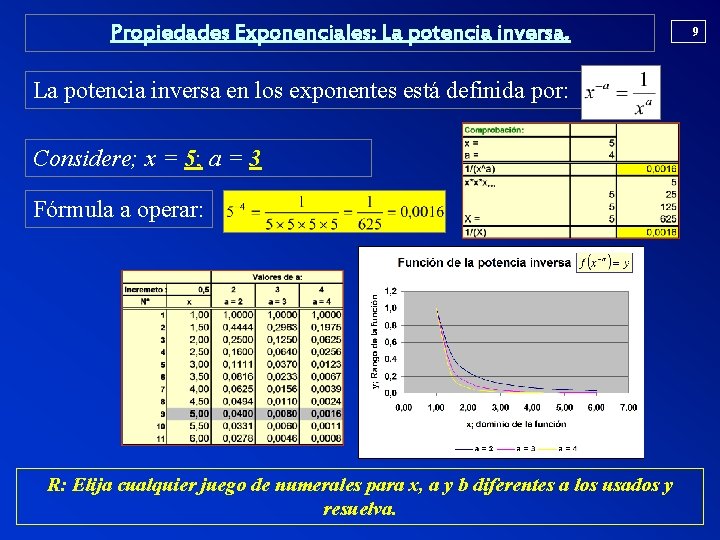
Propiedades Exponenciales: La potencia inversa en los exponentes está definida por: Considere; x = 5; a = 3 Fórmula a operar: R: Elija cualquier juego de numerales para x, a y b diferentes a los usados y resuelva. 9

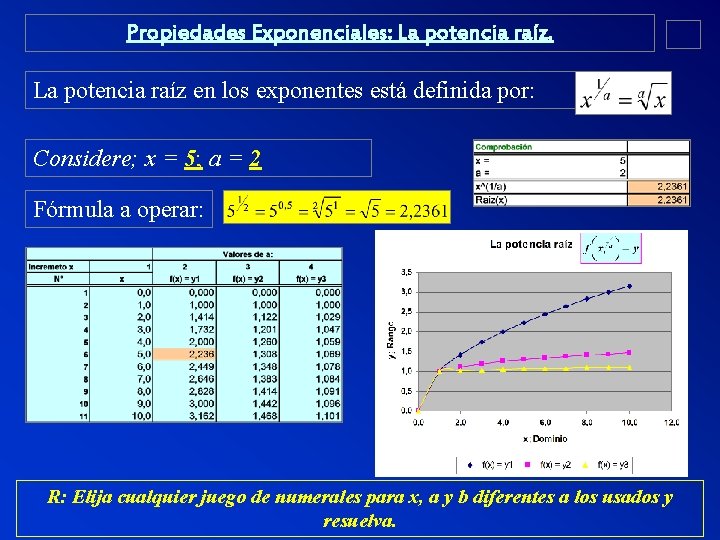
Propiedades Exponenciales: La potencia raíz en los exponentes está definida por: Considere; x = 5; a = 2 Fórmula a operar: R: Elija cualquier juego de numerales para x, a y b diferentes a los usados y resuelva.

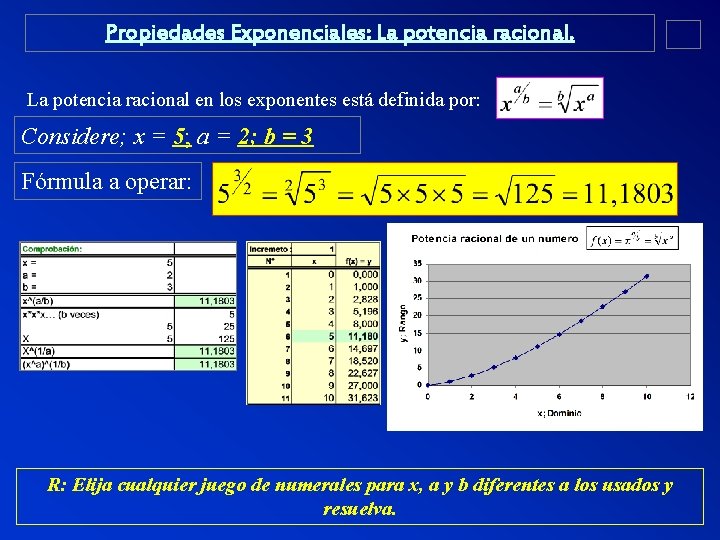
Propiedades Exponenciales: La potencia racional en los exponentes está definida por: Considere; x = 5; a = 2; b = 3 Fórmula a operar: R: Elija cualquier juego de numerales para x, a y b diferentes a los usados y resuelva.

Propiedades Logarítmicas: La forma logarítmica esta definida por: Esto se lee como: y es exponente al que debe elevarse a para obtener x Considere En otras palabras: los logaritmos son exponentes para una base cuya potencia arrojan el valor del número.

3. 13 Logaritmos y bases de uso común. Logaritmo de base 10. Se dice que todo número positivo N puede expresarse como una potencia de 10, es decir, se pueden encontrar siempre una base a tal que N = 10 a. Se dice que y es el logaritmo de N en base 10 = a o logaritmo decimal de N. Se puede escribir: Por ejemplo; 1. 000 = 103, por tanto, log 10 1. 000 = 3. Análogamente, como: 0, 01 = 10– 2, log 10 0, 01= – 2 Cuando N es un número entre 1 y 10, es decir 100 y 101, a log 10 N está comprendido entre 0 y 1. Logaritmo neperiano. Existe un logaritmos muy especial en la matemática conocido como Logaritmo Neperiano cuya base es 2, 71828183… que por su importancia se conoce como Logaritmo Natural y la instrucción para calcular el logaritmo natural de cualquier número (excepto 0) en la Hoja Electrónica es =LN(Número).

Propiedades Logarítmicas: La multiplicación en los logaritmos está definida por: Considere; x = 2. 350; y = 2. 410 Logaritmo de base 10 La función inversa Logaritmo natural La función inversa R: Elija cualquier juego de numerales para x, y, diferentes a los usados y resuelva.

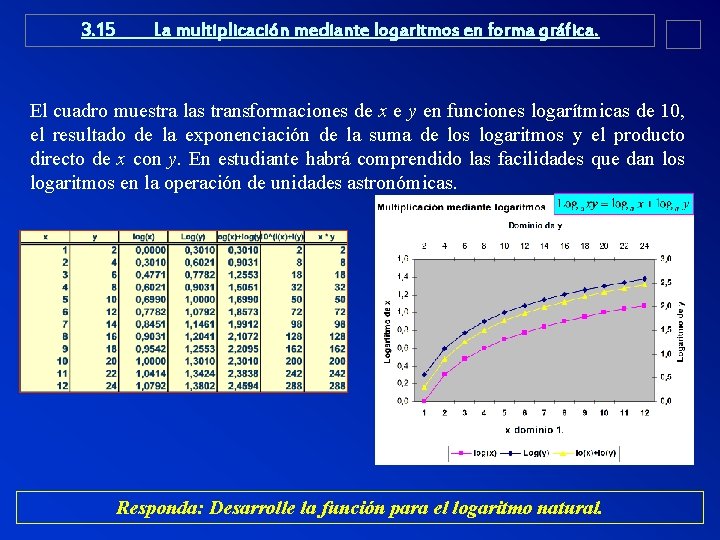
3. 15 La multiplicación mediante logaritmos en forma gráfica. El cuadro muestra las transformaciones de x e y en funciones logarítmicas de 10, el resultado de la exponenciación de la suma de los logaritmos y el producto directo de x con y. En estudiante habrá comprendido las facilidades que dan los logaritmos en la operación de unidades astronómicas. Responda: Desarrolle la función para el logaritmo natural.

Propiedades Logarítmicas: La division. La división en los logaritmos está definida por: Considere: x = 4. 230; y = 3. 230 Logaritmo de base 10 La función inversa Logaritmo natural La función inversa R: Elija cualquier juego de numerales para x, y, diferentes a los usados y resuelva.

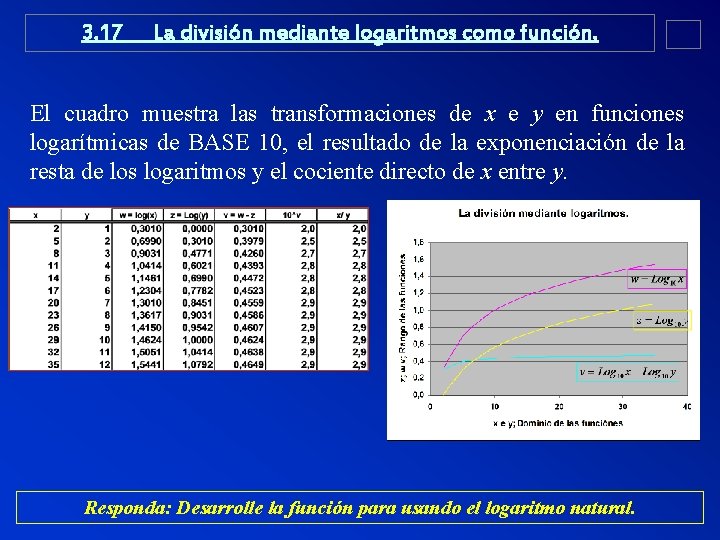
3. 17 La división mediante logaritmos como función. El cuadro muestra las transformaciones de x e y en funciones logarítmicas de BASE 10, el resultado de la exponenciación de la resta de los logaritmos y el cociente directo de x entre y. Responda: Desarrolle la función para usando el logaritmo natural.

Propiedades Logarítmicas: La potencia en los logaritmos está definida por: Considere: x = 50; b = 4 Logaritmo de base 10 La función inversa Logaritmo natural La función inversa R: Elija cualquier juego de numerales para x, b, diferentes a los usados y resuelva.

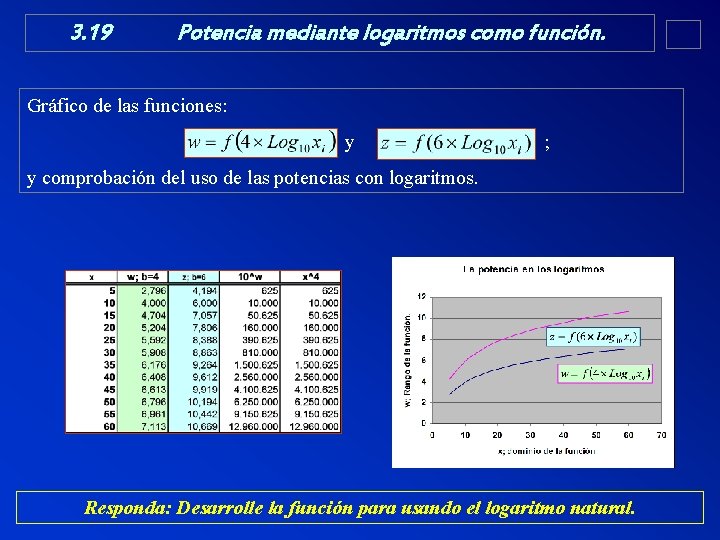
3. 19 Potencia mediante logaritmos como función. Gráfico de las funciones: y ; y comprobación del uso de las potencias con logaritmos. Responda: Desarrolle la función para usando el logaritmo natural.

Propiedades Logarítmicas: Propiedad de identidad y propiedad de cambio de base. La propiedad de identidad esta definida por: En esta propiedad de identidad debe entenderse que los logaritmos de los números x e y son iguales, si la base a que hay que elevar con el logaritmo da un número idéntico: La propiedad del cambio de base: Si x, y, z son números positivos, además x e y son diferentes de 1, entonces:

Algunas soluciones de ecuaciones logarítmicas: Pregunta: Escriba log 1. 000 = 3 en forma exponencial. Respuesta: 1. 000 = 103 Pregunta: Resuelva

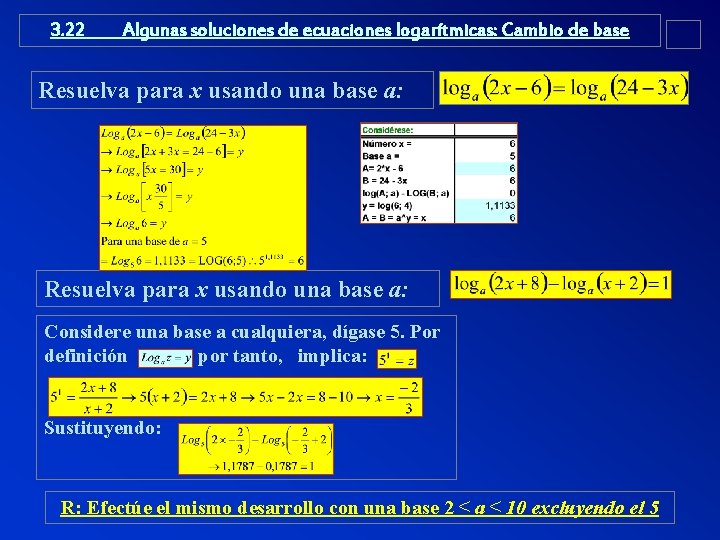
3. 22 Algunas soluciones de ecuaciones logarítmicas: Cambio de base Resuelva para x usando una base a: Considere una base a cualquiera, dígase 5. Por definición por tanto, implica: Sustituyendo: R: Efectúe el mismo desarrollo con una base 2 ≤ a ≤ 10 excluyendo el 5

3. 23 Soluciones a ecuaciones logarítmicas: Potencia inversa. Usando logax = y, resuelva: Por definición: Resolviendo para x potenciando ambos lados por – 3: Recuerde que afectando a ambos lado de una igualdad por el mismo valor no se altera el resultado R: Efectúe el mismo desarrollo con una base 2 ≤ a ≤ 10 excluyendo el 5

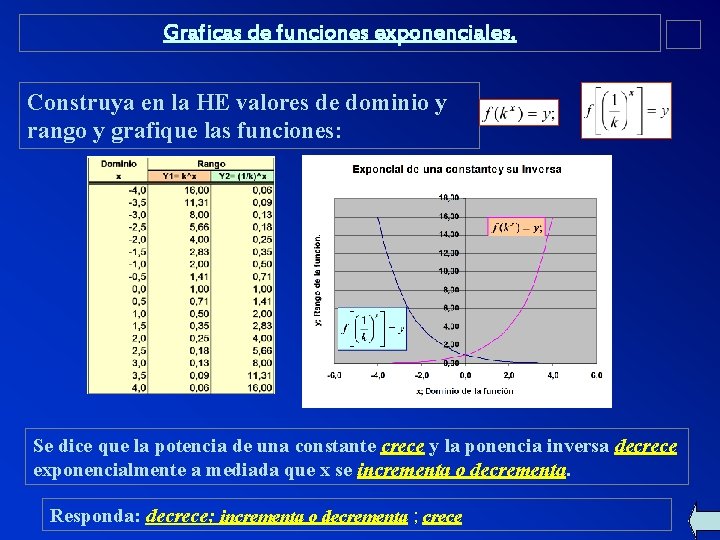
Graficas de funciones exponenciales. Construya en la HE valores de dominio y rango y grafique las funciones: Se dice que la potencia de una constante crece y la ponencia inversa decrece exponencialmente a mediada que x se incrementa o decrementa. Responda: decrece; incrementa o decrementa ; crece

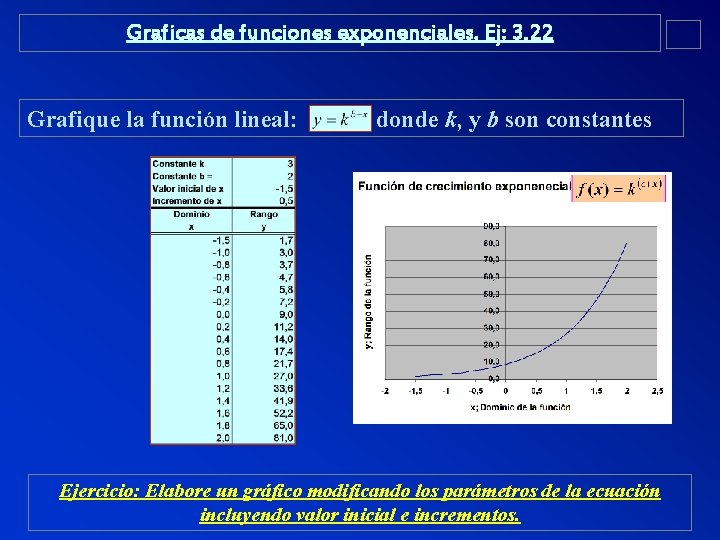
Graficas de funciones exponenciales. Ej: 3, 22 Grafique la función lineal: donde k, y b son constantes Ejercicio: Elabore un gráfico modificando los parámetros de la ecuación incluyendo valor inicial e incrementos.

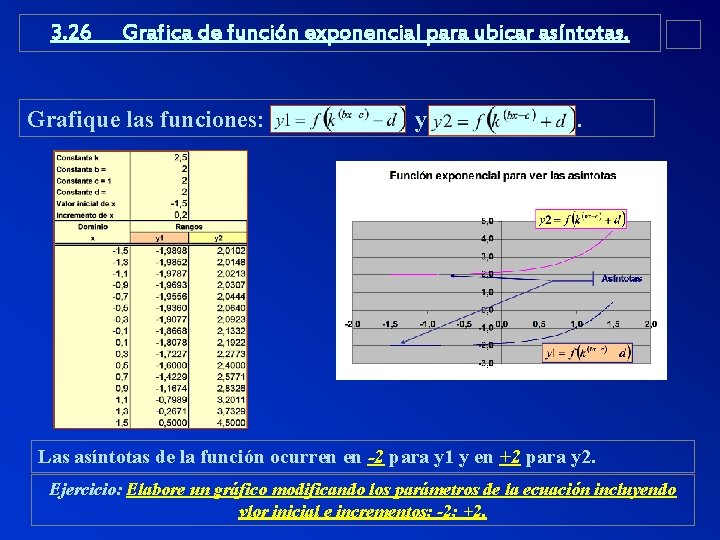
3. 26 Grafica de función exponencial para ubicar asíntotas. Grafique las funciones: y . Las asíntotas de la función ocurren en -2 para y 1 y en +2 para y 2. Ejercicio: Elabore un gráfico modificando los parámetros de la ecuación incluyendo vlor inicial e incrementos; -2; +2.

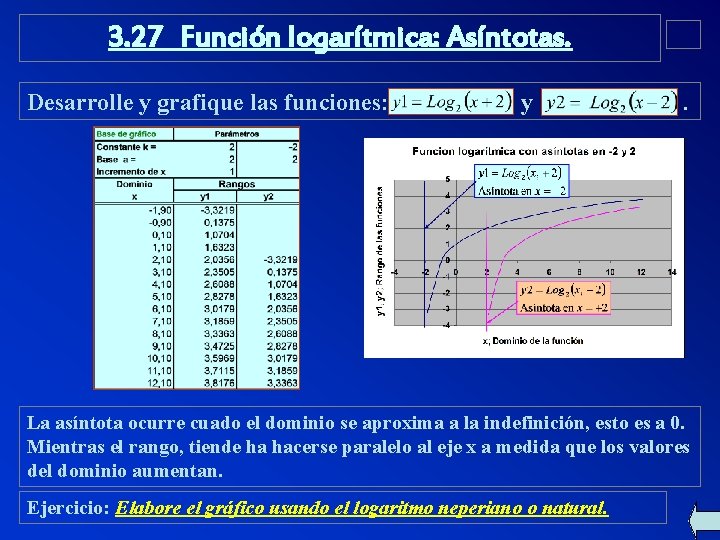
3. 27 Función logarítmica: Asíntotas. Desarrolle y grafique las funciones: y . La asíntota ocurre cuado el dominio se aproxima a la indefinición, esto es a 0. Mientras el rango, tiende ha hacerse paralelo al eje x a medida que los valores del dominio aumentan. Ejercicio: Elabore el gráfico usando el logaritmo neperiano o natural.

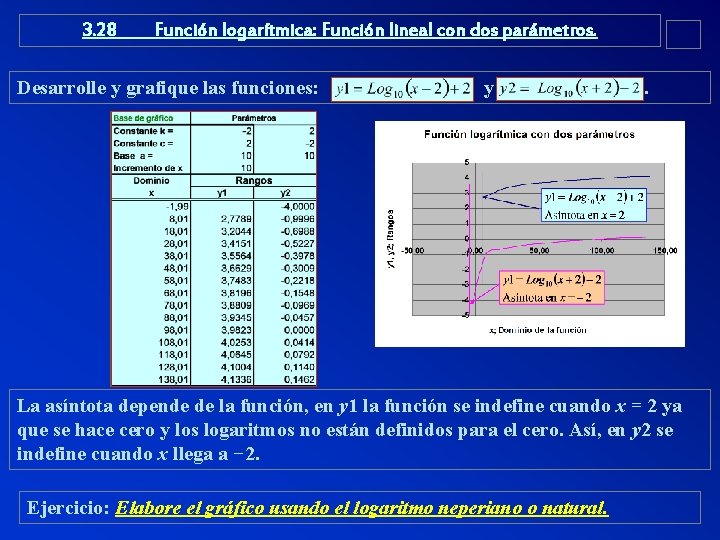
3. 28 Función logarítmica: Función lineal con dos parámetros. Desarrolle y grafique las funciones: y . La asíntota depende de la función, en y 1 la función se indefine cuando x = 2 ya que se hace cero y los logaritmos no están definidos para el cero. Así, en y 2 se indefine cuando x llega a − 2. Ejercicio: Elabore el gráfico usando el logaritmo neperiano o natural.

Resumen de las operaciones exponenciales Multiplicación: División: Propiedad distributiva con multiplicación: Propiedad distributiva con división: Potencia de una potencia: Potencia Inversa: Potencia Racional: Las funciones exponenciales se hacen asintóticas al eje y. Responda: eje x; eje y.

Resumen de las operaciones logarítmicas Forma logarítmica: a = base; b = Número; y = exponente. En donde y es la cantidad a la que hay que elevar a para obtener x. Multiplicación: División: Potencia: Propiedad de identidad: Propiedad de cambio de base: si x, y y z son números positivos, y si x e y diferentes de 1, entonces Las funciones logarítmicas se hacen asintóticas al eje x. Responda: eje x; eje y.

Resumen El capítulo 3 del curso denominado Precálculo dedicado a exponentes y logaritmos contiene el material didáctico necesario para que el estudiante cuente con una base mínima sólida para comprender cursos de cálculo u álgebra avanzados y de la estadística que usualmente se imparte a carreras que no son del área de la matemática. Consta de tres herramientas computacionales cuyos fines son complementarios: El editor de textos que contiene el material del curso con respuestas en bastardilla de color azul; el Libro Electrónico que contiene las operaciones ejemplificadas y el ejercicio mínimo para el estudiante; y este proyector de diapositivas cuyo objeto es que sea elaborado complemento del estudiante con ejercicios particularizados. Manuel Pontigo Alvarado, Enero 2007.