Mathematical Preliminaries 1 Mathematical Preliminaries Sets Functions Relations








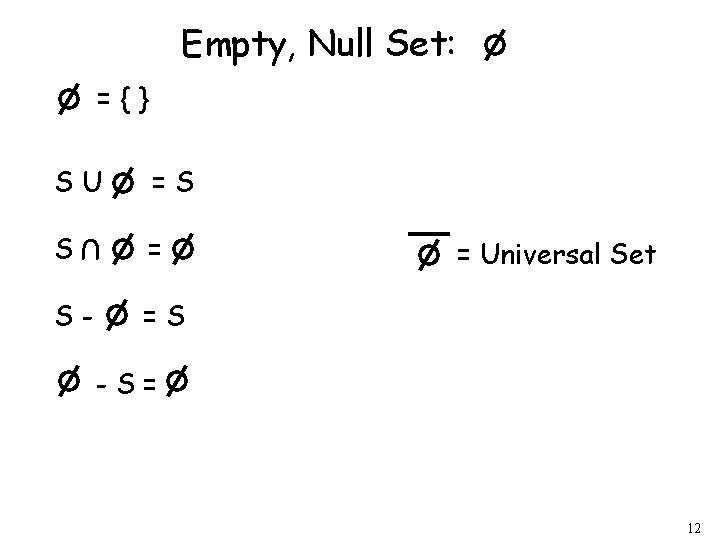




















- Slides: 50

Mathematical Preliminaries 1

Mathematical Preliminaries • Sets • Functions • Relations • Graphs • Proof Techniques 2

SETS A set is a collection of elements We write 3

Sets – Cardinality of a set is the number of elements in the set |{a, b, c}| = 3 |{{a, b}, c}| = 2 ({a, b} and c) 4

Sets – Subsets & Supersets A is a subset of B, A ⊆ B if: ∀x, x ∈ A ⇒ x ∈ B ∀(x ∈ A), x ∈ B A is a proper subset of B, A ⊂ B if: A ⊆ B ∧ (∃x, x ∈ B ∧ x A) {} is a subset of any set (including itself) {} is the only set that does not have a proper subset 5

Set Representations C = { a, b, c, d, e, f, g, h, i, j, k } C = { a, b, …, k } finite set S = { 2, 4, 6, … } infinite set S = { j : j > 0, and j = 2 k for some k>0 } S = { j : j is nonnegative and even } 6

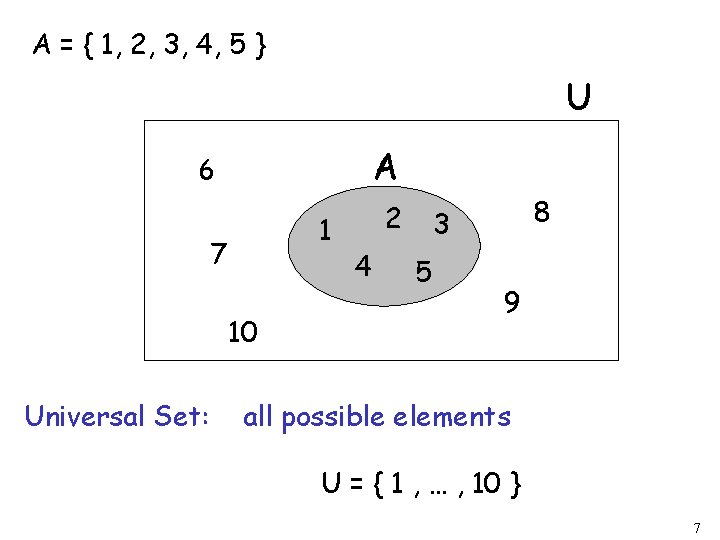
A = { 1, 2, 3, 4, 5 } U A 6 1 7 10 Universal Set: 2 4 8 3 5 9 all possible elements U = { 1 , … , 10 } 7

Set Operations A = { 1, 2, 3 } B = { 2, 3, 4, 5} B A • Union A U B = { 1, 2, 3, 4, 5 } 2 3 1 4 5 • Intersection U A B = { 2, 3 } 2 3 • Difference A-B={1} B - A = { 4, 5 } 1 Venn diagrams 8

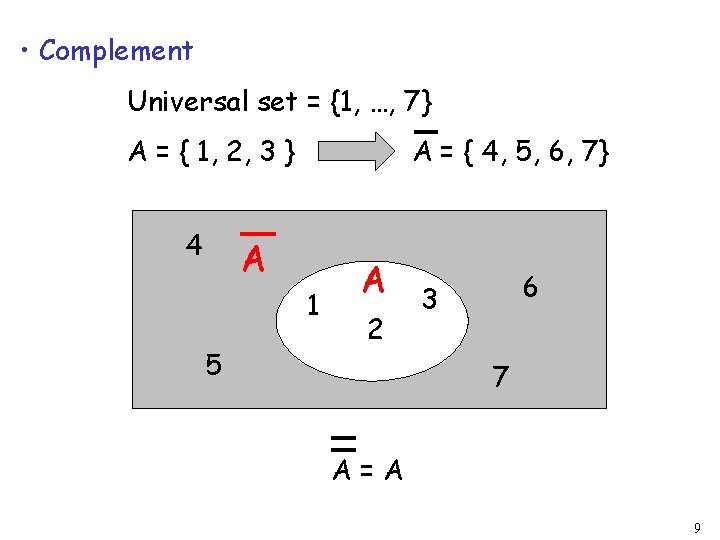
• Complement Universal set = {1, …, 7} A = { 1, 2, 3 } 4 A = { 4, 5, 6, 7} A 1 5 A 2 6 3 7 A=A 9

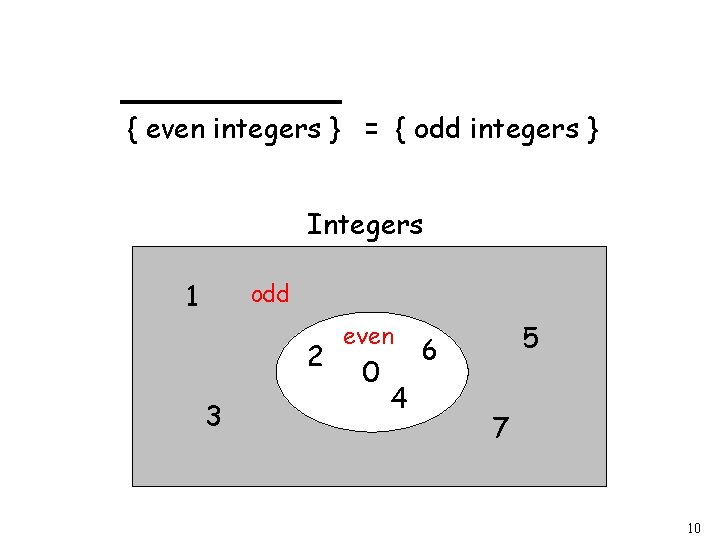
{ even integers } = { odd integers } Integers 1 odd 2 3 even 0 4 5 6 7 10

De. Morgan’s Laws U AUB=A B B=AUB 11
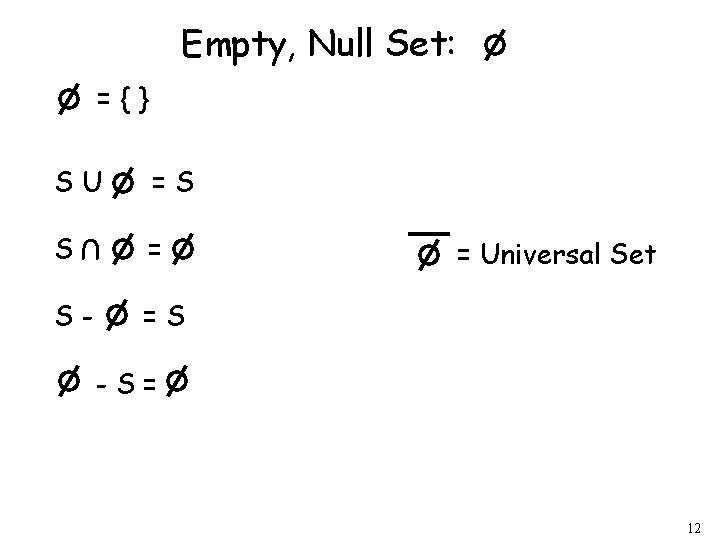
Empty, Null Set: ={} SU =S S = U S- = Universal Set =S -S= 12

Subset A = { 1, 2, 3} B = { 1, 2, 3, 4, 5 } B U Proper Subset: A U A B B A 13

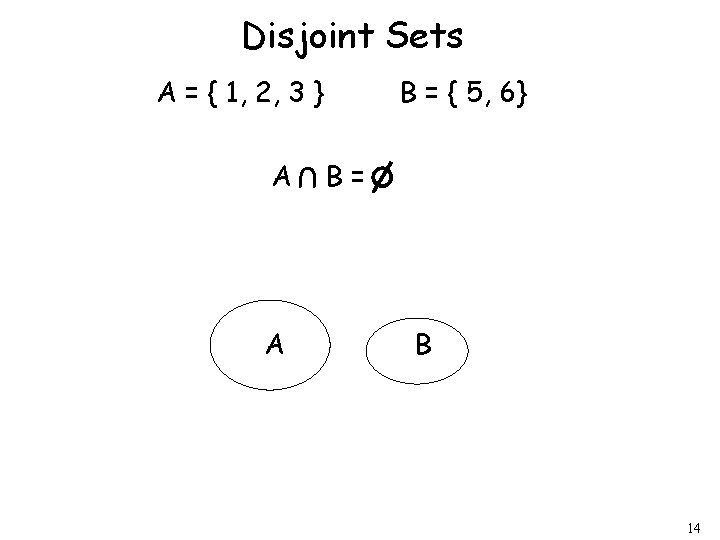
Disjoint Sets A = { 1, 2, 3 } A U A B = { 5, 6} B= B 14

Set Cardinality • For finite sets A = { 2, 5, 7 } |A| = 3 (set size) 15

Powersets A powerset is a set of sets S = { a, b, c } Powerset of S = the set of all the subsets of S 2 S = { , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} } Observation: | 2 S | = 2|S| ( 8 = 23 ) 16

Relations A relation R is a set of ordered pairs For example the relation < over the Natural Numbers is the set: { (0, 1), (0, 2), (0, 3), . . . (1, 2), (1, 3), (1, 4), . . . (2, 3), (2, 4), (2, 5), . . . } 17

Relations Often, relations are over the same set that is, a subset of A × A for some set A Not all relations are over the same set, however Relation describing prices of computer components {(Hard dive, $55), (WAP, $49), (256 M DDR, $44), . . . } 18

Relations Q and R are two relations The composition of Q and R, Q ◦ R is: {(a, b) : (a, c) ∈ Q, (c, b) ∈ R for some c} Q = {(a, c), (b, d), (c, a)} R = {(a, c), (b, c), (c, a)} Q ◦ R = {(a, a), (c, c)} Q ◦ Q ? (Q ◦ R) ◦ Q? 19

Relation Graph Each element is a node in the graph if (a, b) ∈ R, then there is an edge from a to b in the graph R = {(a, b), (a, c), (c, a), (b, b), (b, d)} 20

Functions A function is a special kind of relation (all functions are relations, but not all relations are functions) A relation R ⊆ A × B is a function if: For each a ∈ A, there is exactly one ordered pair in R with the first component a 21

Functions A function f that is a subset of A × B is written: f: A→B (a, b) ∈ f is written f(a) = b A is the domain of the function if A′ ⊆ A, f(A′) = {b : a ∈ A′ ∧ f(a) = b} is the image of A′ The range of a function is the image of its domain 22

Functions A function f : A → B is: one-to-one if no two elements in A match to the same element in B onto Each element in B is mapped to by at least one element in A a bijection if it is both one-to-one and onto The inverse of a binary relation R ⊂ A × B is denoted R− 1, and defined to be {(b, a) : (a, b) ∈ R} A function only has an inverse if it is a bijection 23

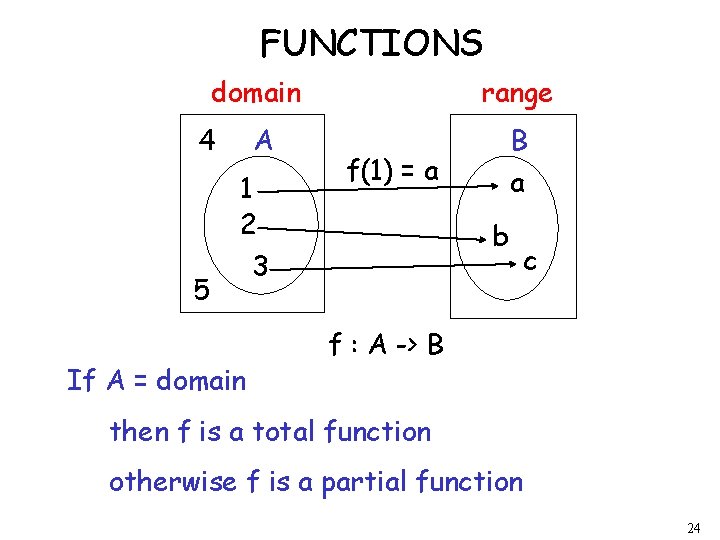
FUNCTIONS domain 4 5 A 1 2 3 If A = domain range B f(1) = a a b c f : A -> B then f is a total function otherwise f is a partial function 24

GRAPHS A directed graph e b node d a edge c • Nodes (Vertices) V = { a, b, c, d, e } • Edges E = { (a, b), (b, c), (b, e), (c, a), (c, e), (d, c), (e, b), (e, d) } 25

Labeled Graph 2 6 a b 1 5 3 e 6 2 d c 26

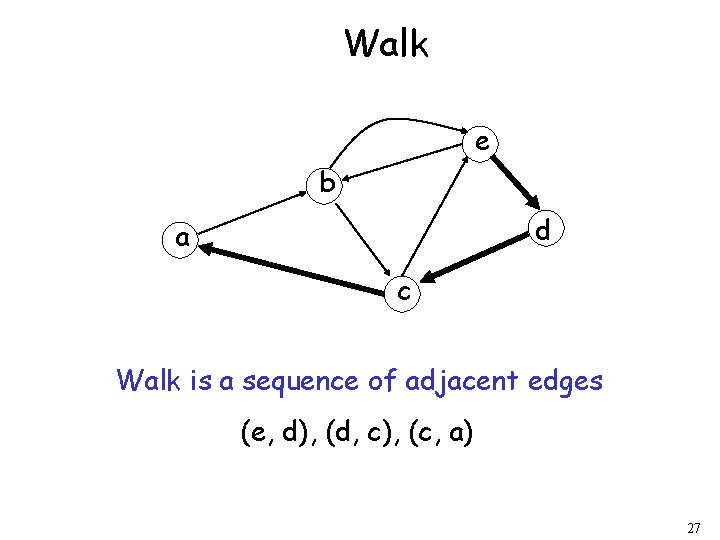
Walk e b d a c Walk is a sequence of adjacent edges (e, d), (d, c), (c, a) 27

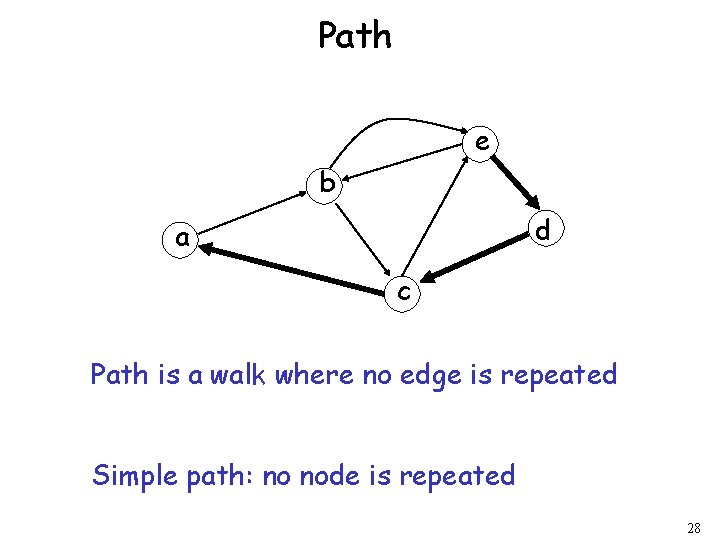
Path e b d a c Path is a walk where no edge is repeated Simple path: no node is repeated 28

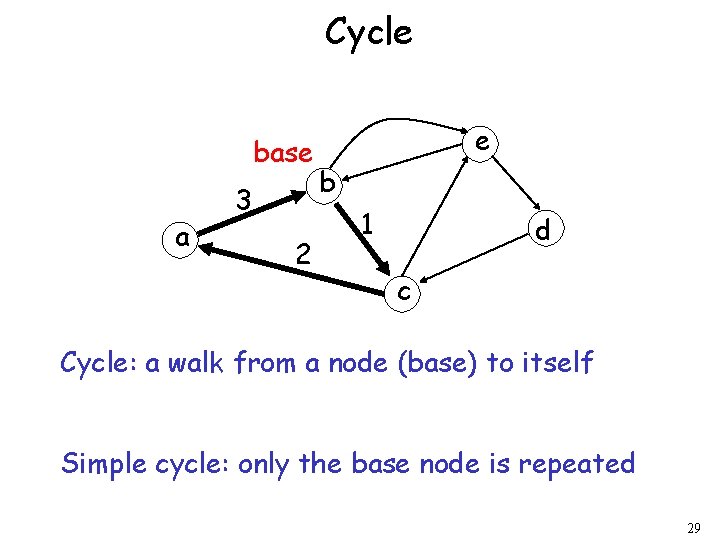
Cycle base a 3 2 e b 1 d c Cycle: a walk from a node (base) to itself Simple cycle: only the base node is repeated 29

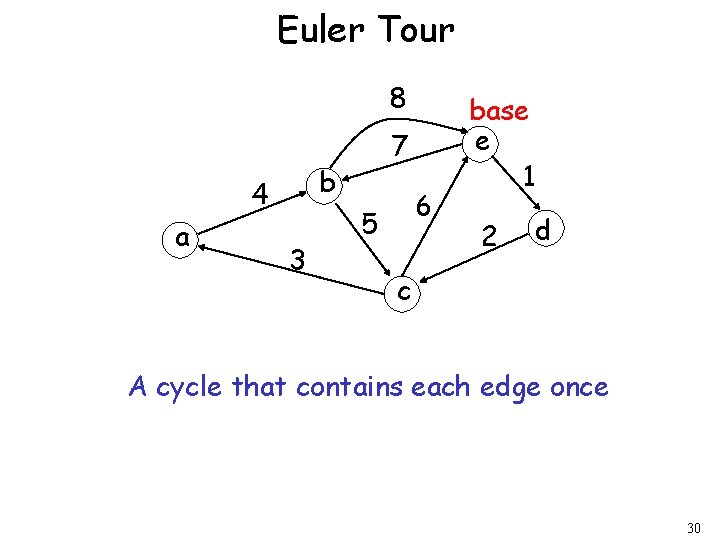
Euler Tour 8 b 4 a 7 3 6 5 base e 1 2 d c A cycle that contains each edge once 30

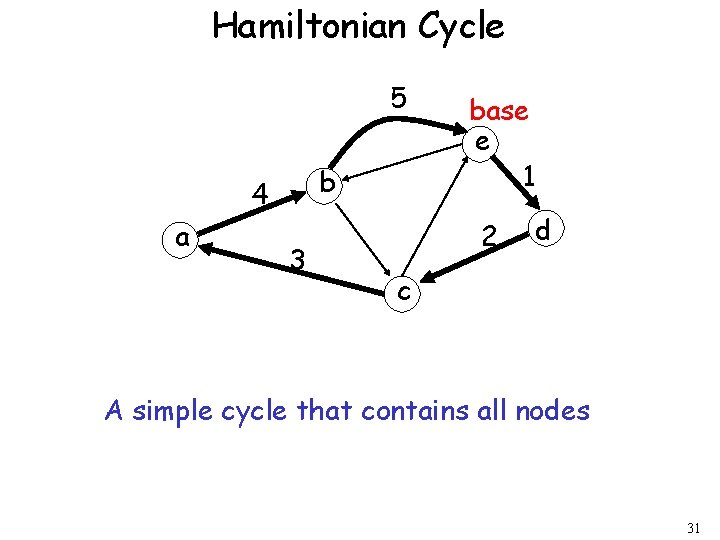
Hamiltonian Cycle 5 b 4 a 3 base e 1 2 d c A simple cycle that contains all nodes 31

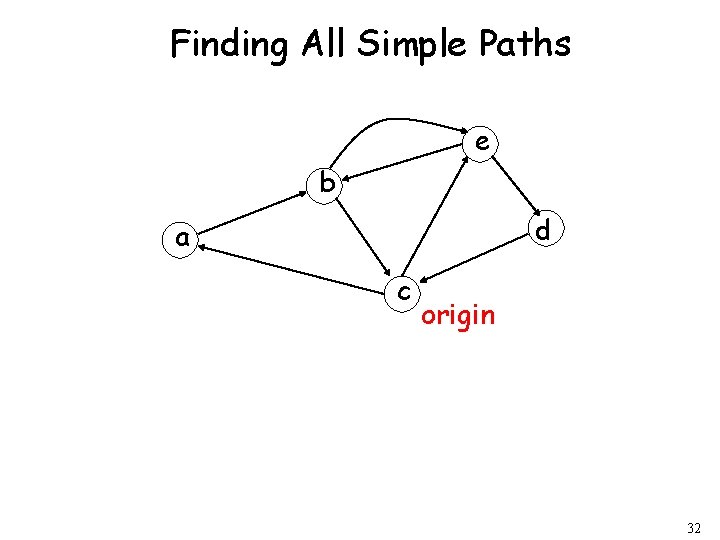
Finding All Simple Paths e b d a c origin 32

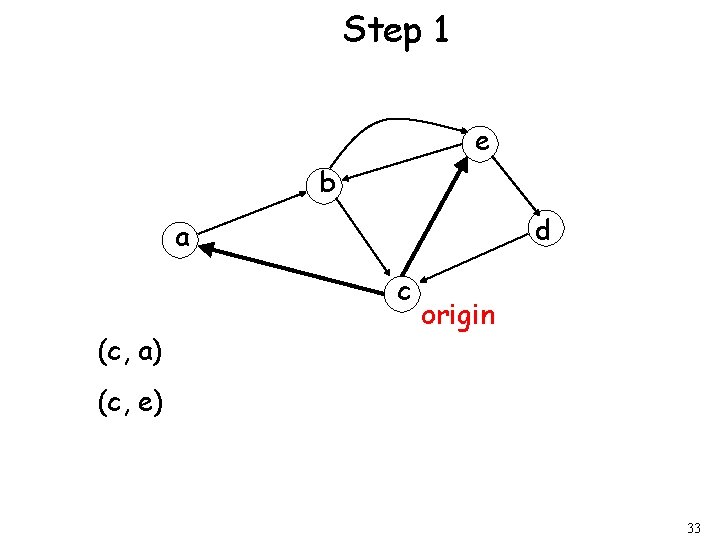
Step 1 e b d a c (c, a) origin (c, e) 33

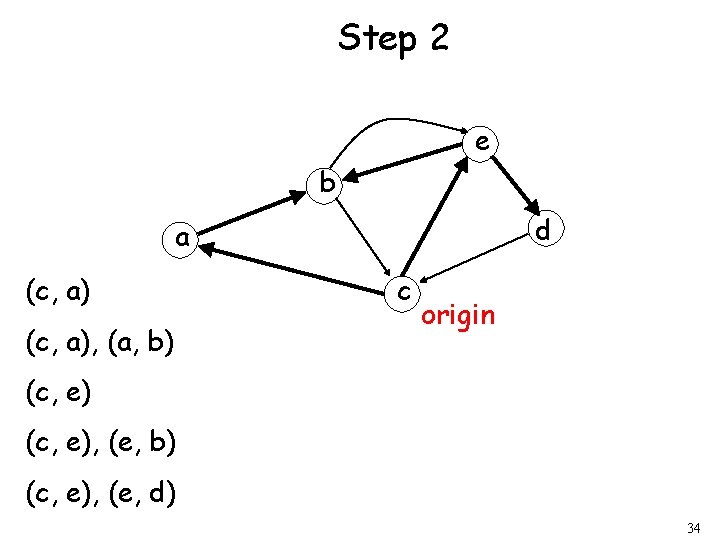
Step 2 e b d a (c, a), (a, b) c origin (c, e), (e, b) (c, e), (e, d) 34

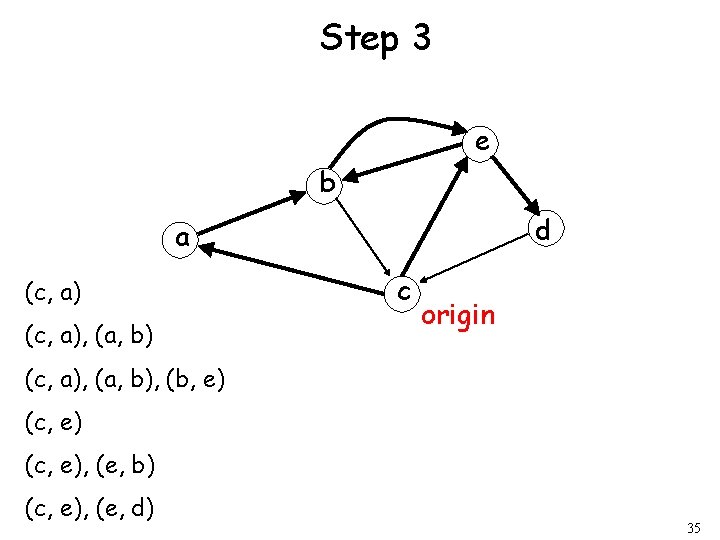
Step 3 e b d a (c, a), (a, b) c origin (c, a), (a, b), (b, e) (c, e), (e, b) (c, e), (e, d) 35

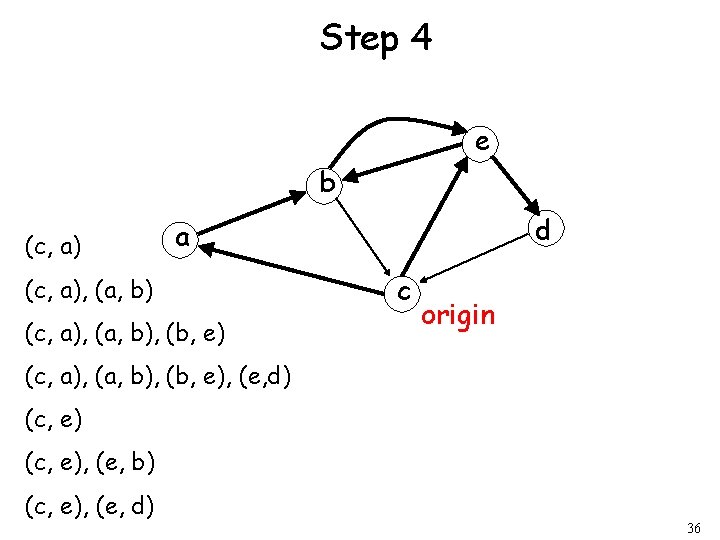
Step 4 e b (c, a) d a (c, a), (a, b), (b, e) c origin (c, a), (a, b), (b, e), (e, d) (c, e), (e, b) (c, e), (e, d) 36

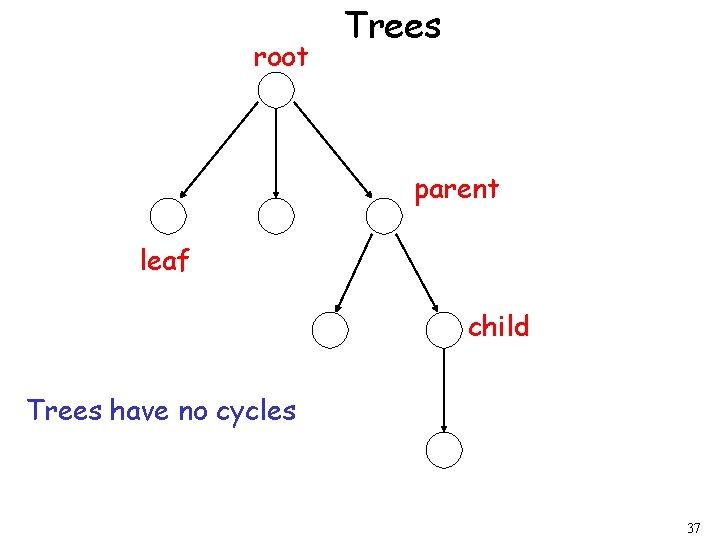
root Trees parent leaf child Trees have no cycles 37

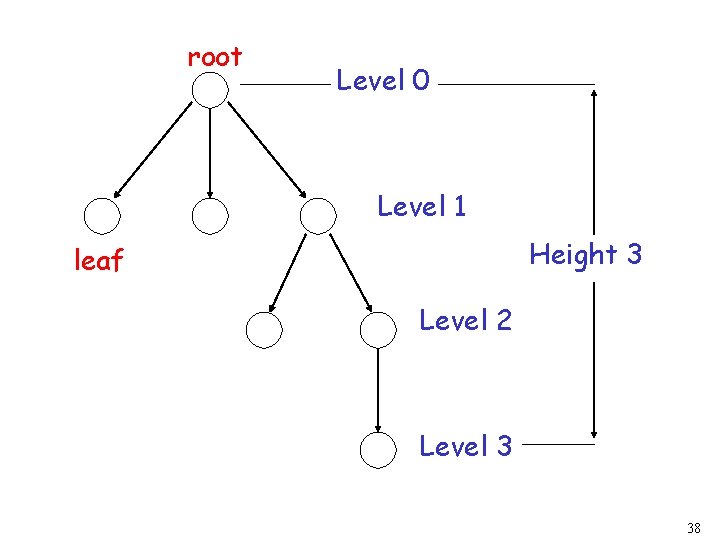
root Level 0 Level 1 Height 3 leaf Level 2 Level 3 38

Binary Trees 39

PROOF TECHNIQUES • Proof by induction • Proof by contradiction 40

Induction We have statements P 1, P 2, P 3, … If we know • for some b that P 1, P 2, …, Pb are true • for any k >= b that P 1, P 2, …, Pk imply Pk+1 Then Every Pi is true 41

Proof by Induction • Inductive basis Find P 1, P 2, …, Pb which are true • Inductive hypothesis Let’s assume P 1, P 2, …, Pk are true, for any k >= b • Inductive step Show that Pk+1 is true 42

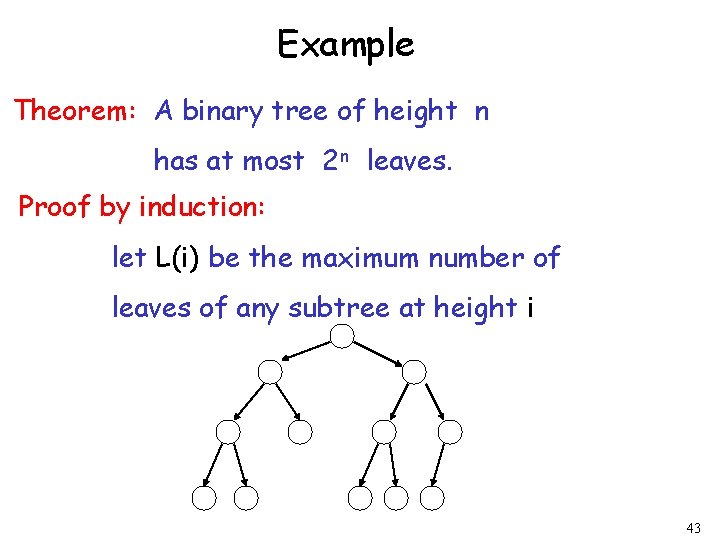
Example Theorem: A binary tree of height n has at most 2 n leaves. Proof by induction: let L(i) be the maximum number of leaves of any subtree at height i 43

We want to show: L(i) <= 2 i • Inductive basis L(0) = 1 (the root node) • Inductive hypothesis Let’s assume L(i) <= 2 i for all i = 0, 1, …, k • Induction step we need to show that L(k + 1) <= 2 k+1 44

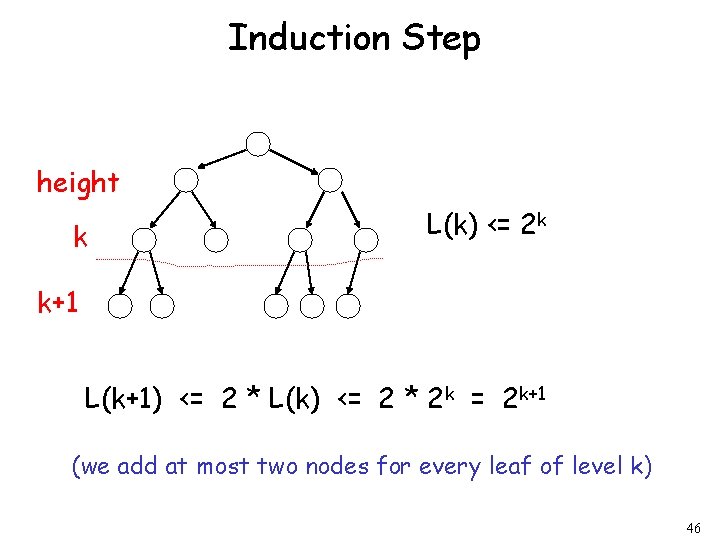
Induction Step height k k+1 From Inductive hypothesis: L(k) <= 2 k 45

Induction Step height k L(k) <= 2 k k+1 L(k+1) <= 2 * L(k) <= 2 * 2 k = 2 k+1 (we add at most two nodes for every leaf of level k) 46

Remark Recursion is another thing Example of recursive function: f(n) = f(n-1) + f(n-2) f(0) = 1, f(1) = 1 47

Proof by Contradiction We want to prove that a statement P is true • we assume that P is false • then we arrive at an incorrect conclusion • therefore, statement P must be true 48

Example Theorem: is not rational Proof: Assume by contradiction that it is rational = n/m n and m have no common factors We will show that this is impossible 49

= n/m Therefore, 2 m 2 = 4 k 2 n 2 2 m 2 = n 2 is even m 2 = 2 k 2 n is even n=2 k m is even m=2 p Thus, m and n have common factor 2 Contradiction! 50
 Mathematical preliminaries in numerical computing
Mathematical preliminaries in numerical computing Chapter 1 mathematical preliminaries
Chapter 1 mathematical preliminaries Apa itu preliminaries
Apa itu preliminaries Preliminary materials
Preliminary materials Halaman preliminaries
Halaman preliminaries Roles synoynm
Roles synoynm Employee relations in public relations
Employee relations in public relations Correspondence function examples
Correspondence function examples Mathematical economics vs non mathematical economics
Mathematical economics vs non mathematical economics Relation and function example
Relation and function example 1-2 practice analyzing graphs of functions and relations
1-2 practice analyzing graphs of functions and relations Inverse relations and functions
Inverse relations and functions Functions vs relations
Functions vs relations Lesson 2-1 relations and functions
Lesson 2-1 relations and functions 7-2 inverses of relations and functions
7-2 inverses of relations and functions Inverse variation graph calculator
Inverse variation graph calculator Lesson 4-6 formalizing relations and functions answers
Lesson 4-6 formalizing relations and functions answers 6-2 inverse functions and relations
6-2 inverse functions and relations 4-2 inverses of relations and functions
4-2 inverses of relations and functions 1-2 analyzing graphs of functions and relations
1-2 analyzing graphs of functions and relations 4-2 practice b inverses of relations and functions
4-2 practice b inverses of relations and functions 2-2 linear relations and functions
2-2 linear relations and functions 1-2 analyzing graphs of functions and relations
1-2 analyzing graphs of functions and relations Find two functions defined implicitly by this equation
Find two functions defined implicitly by this equation Function vs relation
Function vs relation Unit 5 lesson 6 formalizing relations and functions
Unit 5 lesson 6 formalizing relations and functions 1-7 inverse relations and functions
1-7 inverse relations and functions 1-7 inverse relations and functions
1-7 inverse relations and functions When is a relation a function
When is a relation a function Characteristics of relations and functions
Characteristics of relations and functions Topic 1 relations and functions
Topic 1 relations and functions Linear relations and functions
Linear relations and functions Vlt and hlt
Vlt and hlt Mathematical functions in java
Mathematical functions in java Sinusoidal functions as mathematical models
Sinusoidal functions as mathematical models Linear functions as mathematical models
Linear functions as mathematical models Linear functions as mathematical models
Linear functions as mathematical models Absolute value piecewise function
Absolute value piecewise function Evaluating functions
Evaluating functions Evaluating functions and operations on functions
Evaluating functions and operations on functions What shape has 2 sets of parallel sides
What shape has 2 sets of parallel sides Lexical sets
Lexical sets Weak entity set example
Weak entity set example Lingo @gin
Lingo @gin Scenario the deputy incident commander will be replacing
Scenario the deputy incident commander will be replacing Information sets in game theory
Information sets in game theory Lexical sets
Lexical sets (a-b)^n formula
(a-b)^n formula Sets and propositions
Sets and propositions Lexical sets
Lexical sets These are predefined sets of different shapes
These are predefined sets of different shapes