CHAPTER 3 Language Theory and Mathematical Preliminaries SETS

CHAPTER 3 Language Theory and Mathematical Preliminaries

SETS A set is a collection of elements We write C = { a, b, c, d, e, f, g, h, i, j, k } C = { a, b, …, k } finite set S = { 2, 4, 6, … } infinite set S = { j : j > 0, and j = 2 k for some k>0 } S = { j : j is nonnegative and even } 1 -2

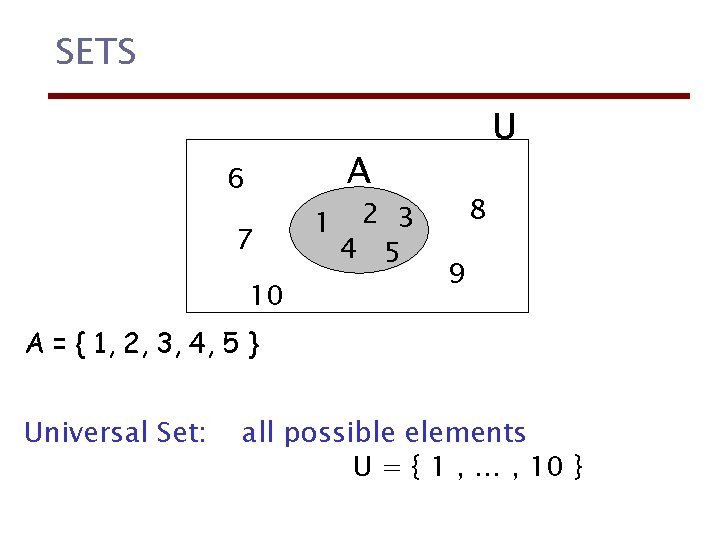
SETS U A 6 7 10 1 2 3 4 5 8 9 A = { 1, 2, 3, 4, 5 } Universal Set: all possible elements U = { 1 , … , 10 }

SETS B A 2 3 1 4 5

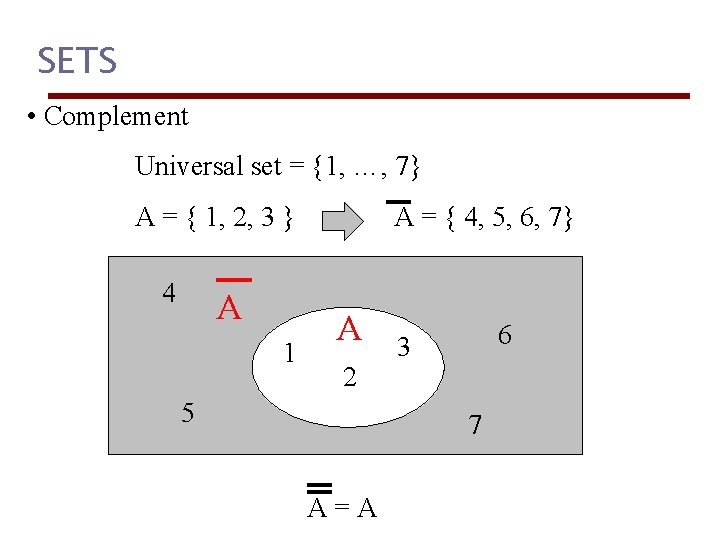
SETS • Complement Universal set = {1, …, 7} A = { 1, 2, 3 } 4 A 1 A = { 4, 5, 6, 7} A 2 5 6 3 7 A=A

SETS Empty Set: A = { 1, 2, 3} B = { 1, 2, 3, 4, 5 } Disjoint Sets: Set Cardinality |A| = 3

SETS A powerset is a set of sets S = { a, b, c } Powerset of S is the set of all the subsets of S 2 S = {∅ , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} } | 2 S | = 2|S| ( 8 = 23 )

THREE BASIC CONCEPTS • Languages • Grammars • Automata

Language A language is a set of strings. String: A sequence of letters defined over an alphabet: Examples: “cat”, “dog”, “house”, …

Language String Concatenation Reverse Length

Language Empty String : A string with no letters • Substring of string: – a subsequence of consecutive characters

Prefix and Suffix Prefixes Suffixes prefix suffix

Language Repeat Operation The * Operation: the set of all possible strings from alphabet

Language The + Operation: Costas Busch - RPI 14

Languages A language is any subset of Languages:

Another Example An infinite language

Operations on Languages • The usual set operations • Complement: Costas Busch - RPI 17

Reverse & Concatation Costas Busch - RPI 18

Repeat Operation

Star-Closure (Kleene *) Example: Costas Busch - RPI 20

Positive Closure

Grammars A grammar for the English language tells us whether a particular sentence is well formed or not. <sentence> → <noun phrase> <predicate> <noun phrase> → <article><noun>, <predicate> → <verb> If we associate the actual words “a” and “the” with <article>, “boy” and “dog” with <noun>, and “runs” and “walks” with <verb>, then the grammar tells us that the sentences “a boy runs” and “the dog walks” are properly formed. Copyright © 2015 Pearson. All rights reserved. 1 -22

Grammars A Grammar G is defined as a quadruple G = (V, T, S, P), where V is a finite set of objects called variables, T is a finite set of objects called terminal symbols, S ∈ V is a special symbol called the start variable, P is a finite set of productions. The production rules are the heart of a grammar; they specify how the grammar transforms one string into another: x → y,

Grammars x→y

Grammars

Grammars

Grammars

Grammars For Find The Language of the following Grammer.

Grammars Consider the grammar G 1 = ({A, S}, {a, b}, S, P), with P consisting of the productions S → a. Ab|λ, A → a. Ab|λ. Find The Language of the following Grammer.

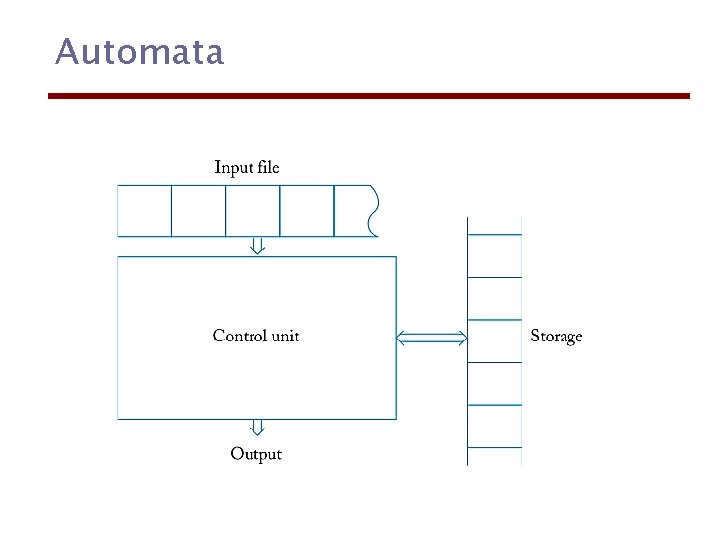
Automata An automaton is an abstract model of a digital computer. It has a mechanism for reading input. Input is a string over a given alphabet. The automaton can produce output of some form. It may have a temporary storage device, consisting of an unlimited number of cells, each capable of holding a single symbol from alphabet. Finally, the automaton has a control unit, which can be in any of a internal states, and can change state in some defined manner.

Automata

Automata The internal state of the control unit at the next time step is determined by the next-state or transition function. Deterministic Automata : each move is uniquely determined by the current configuration. • If we know the internal state, the input, and the contents of the temporary storage, we can predict the future behavior of the automaton exactly. Nondeterministic Automaton: At each point, may have several possible moves, so we can only predict a set of possible actions.

Automata An automaton whose output response is limited to a simple “yes” or “no” is called an accepter. Presented with an input string, an accepter either accepts the string or rejects it. A more general automaton, capable of producing strings of symbols as output, is called a transducer.

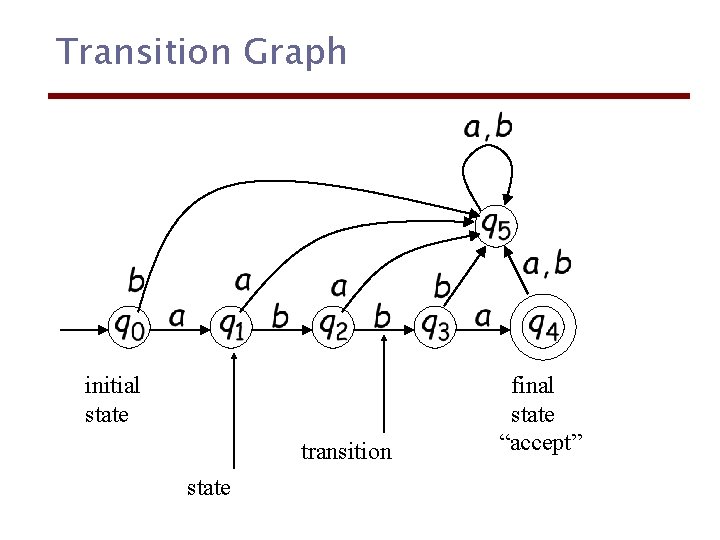
Transition Graph initial state transition state final state “accept”

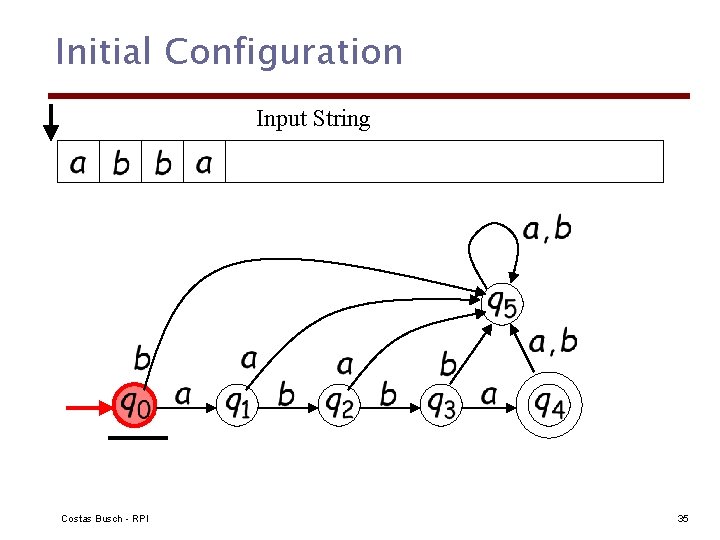
Initial Configuration Input String Costas Busch - RPI 35

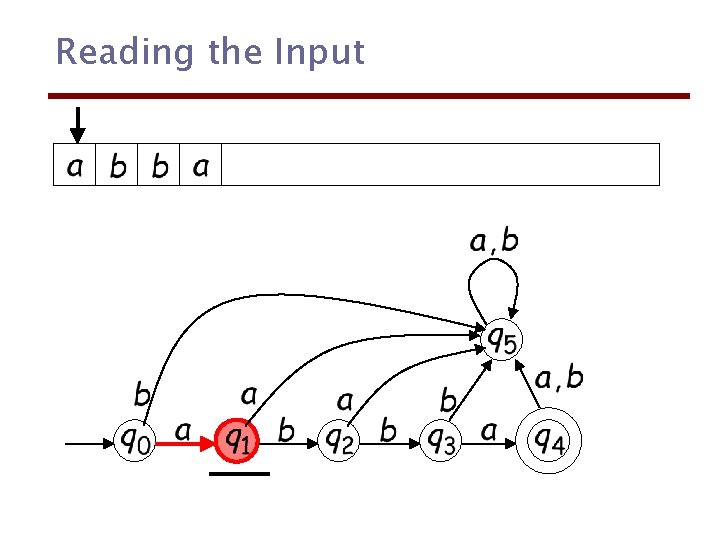
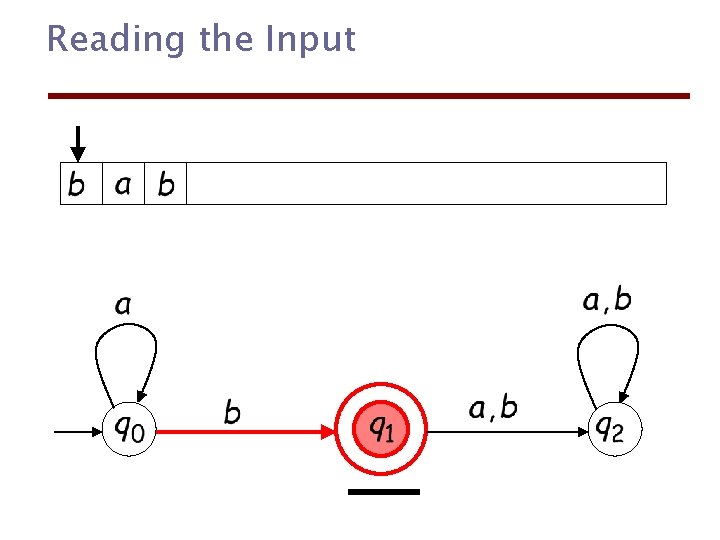
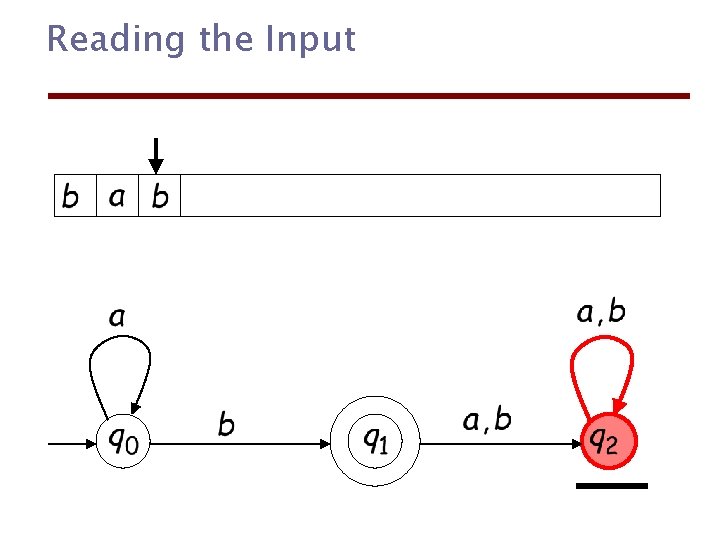
Reading the Input

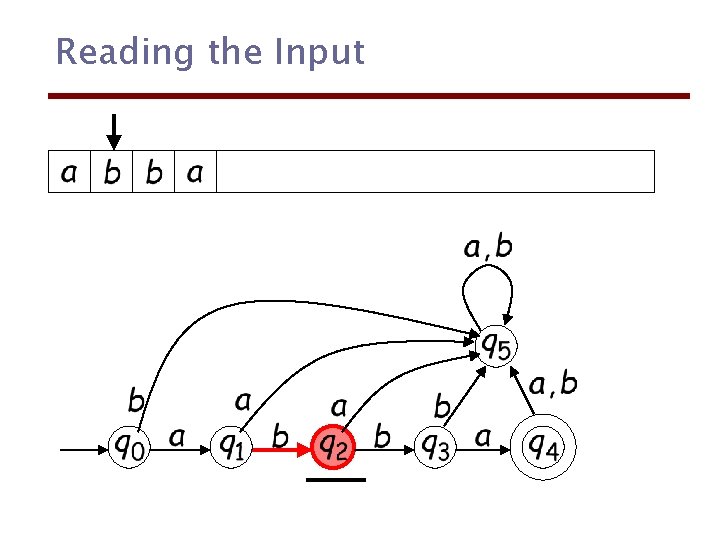
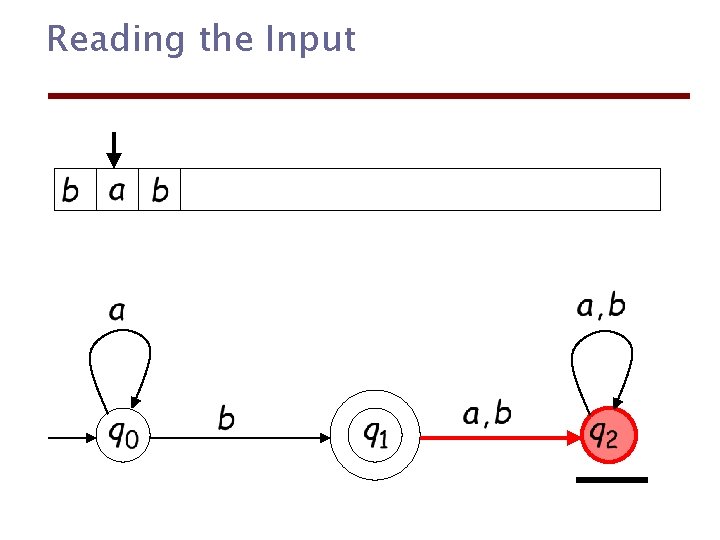
Reading the Input

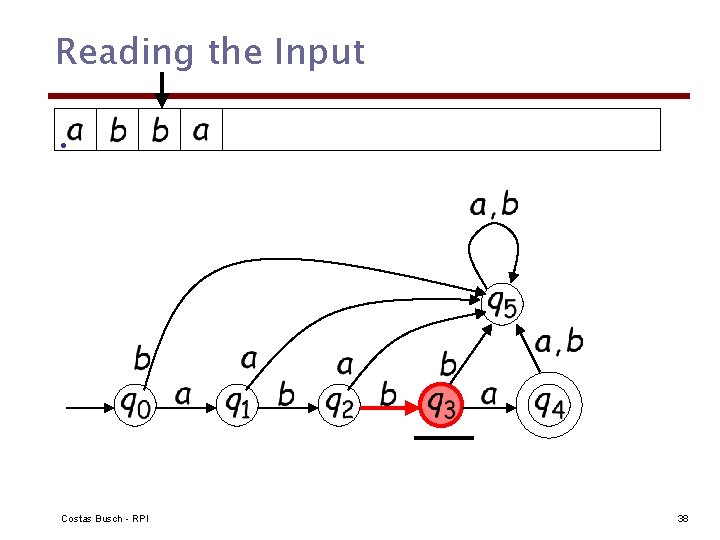
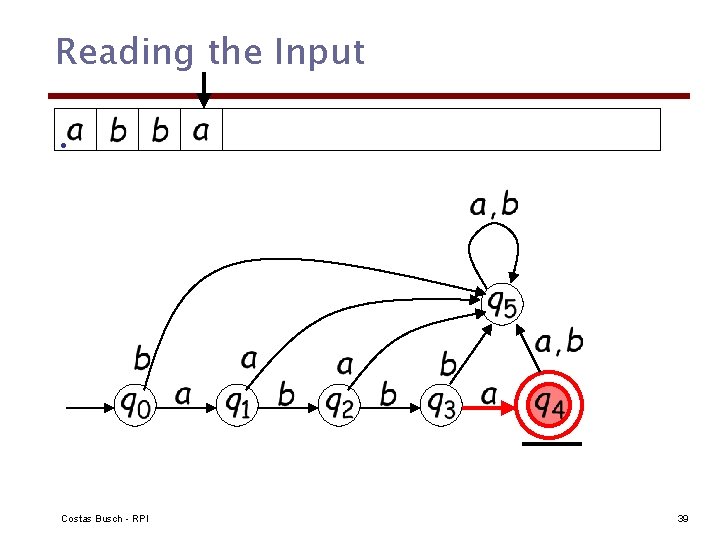
Reading the Input • Costas Busch - RPI 38

Reading the Input • Costas Busch - RPI 39

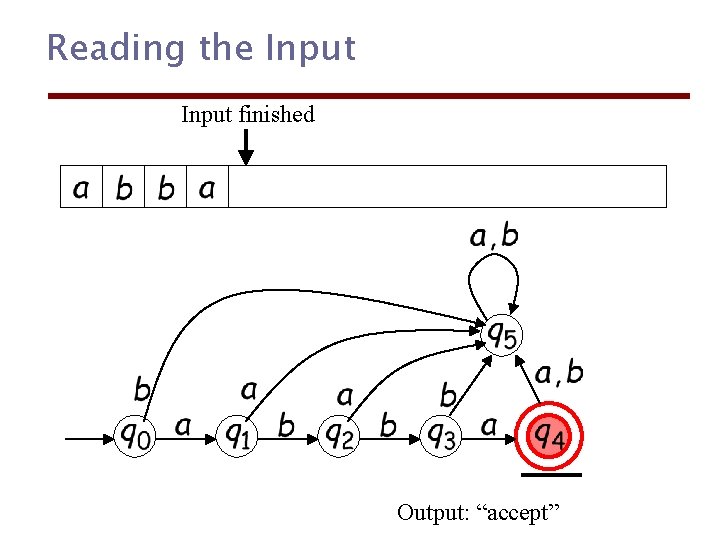
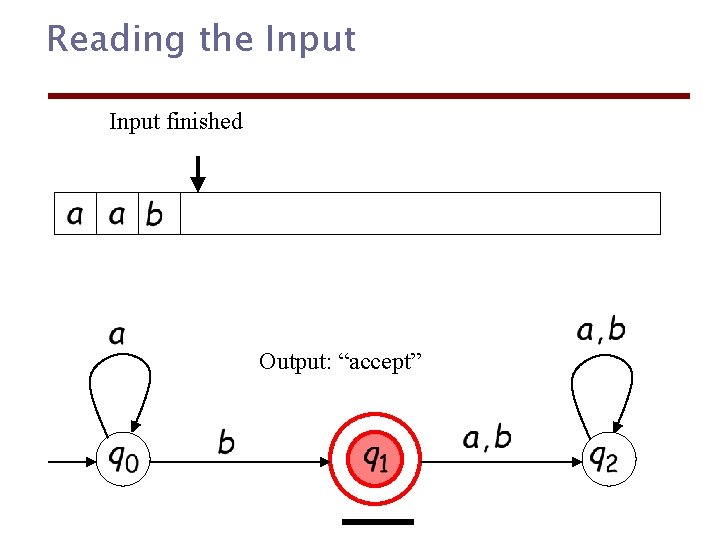
Reading the Input finished Output: “accept”

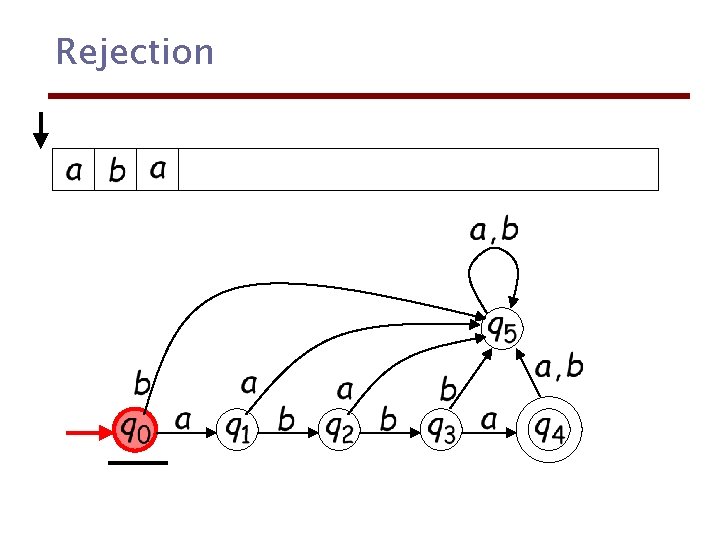
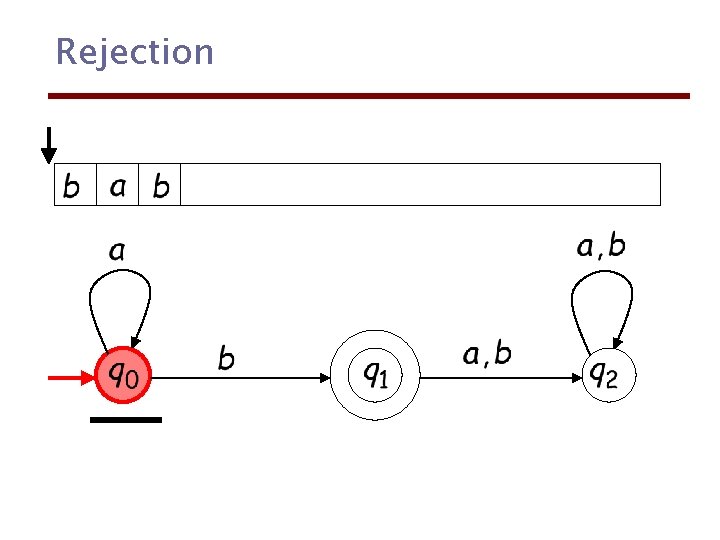
Rejection

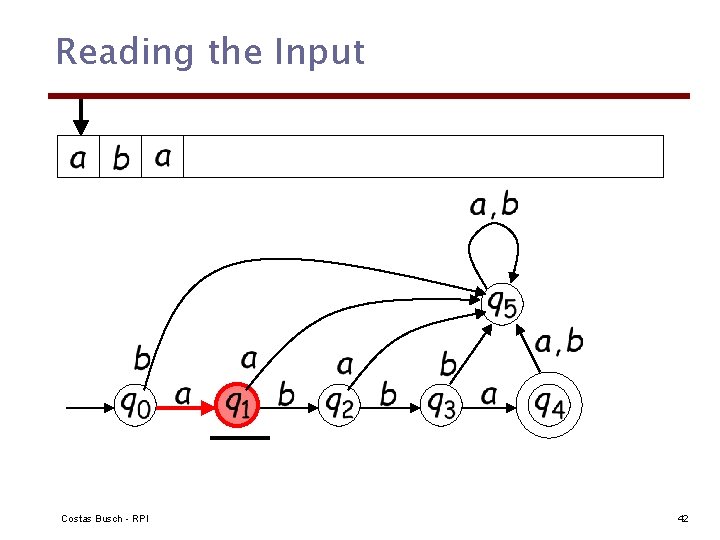
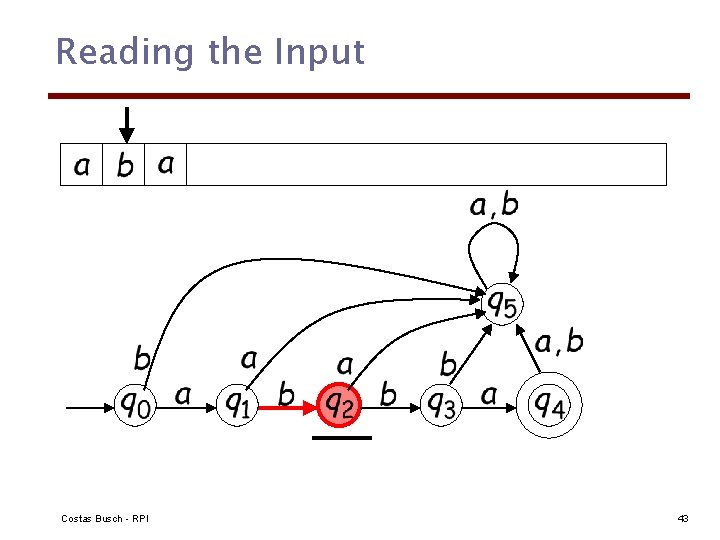
Reading the Input Costas Busch - RPI 42

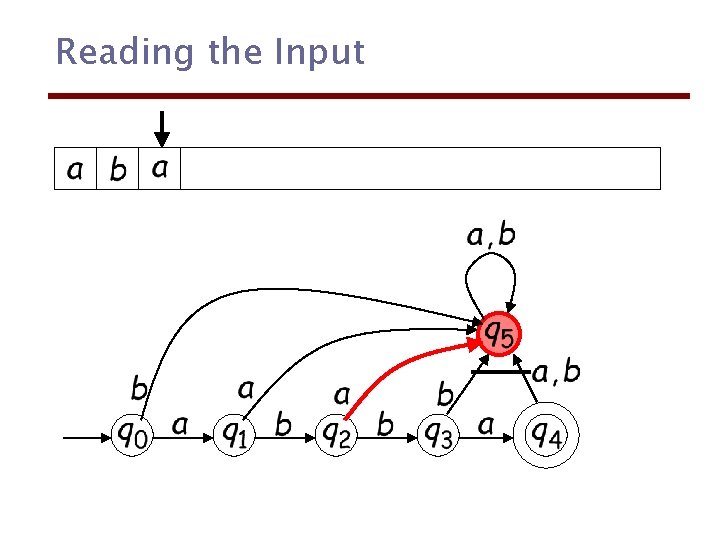
Reading the Input Costas Busch - RPI 43

Reading the Input

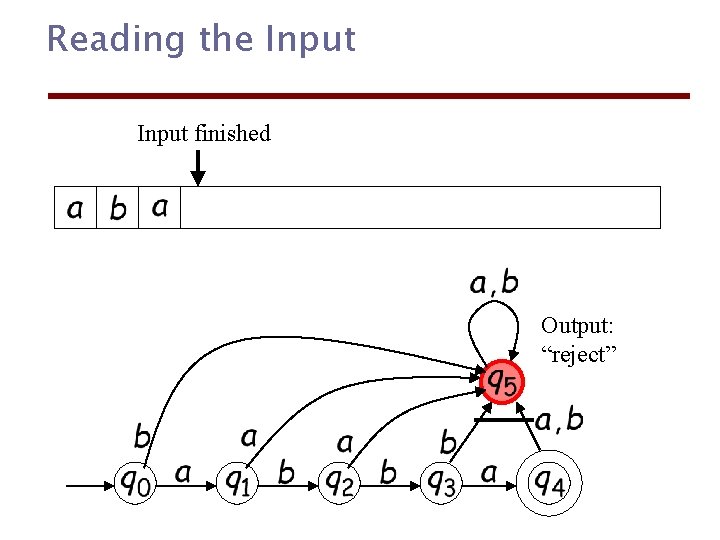
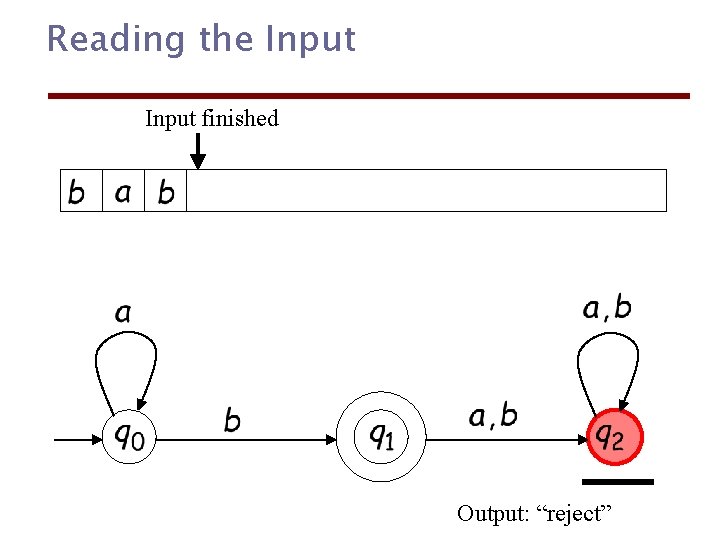
Reading the Input finished Output: “reject”

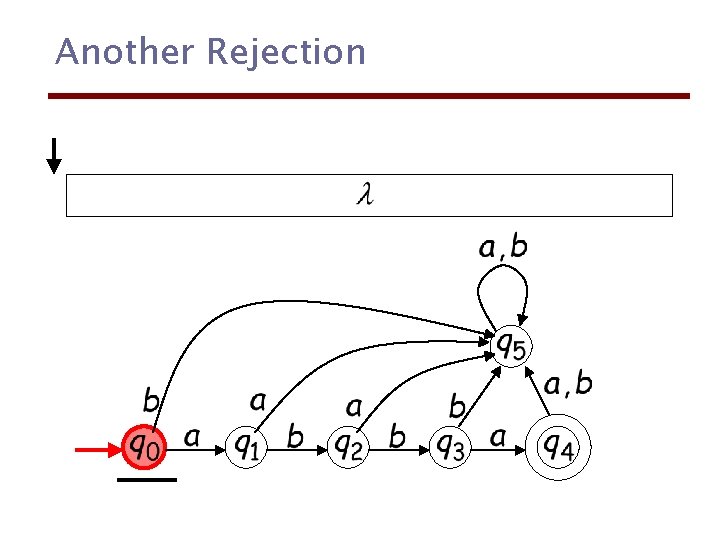
Another Rejection

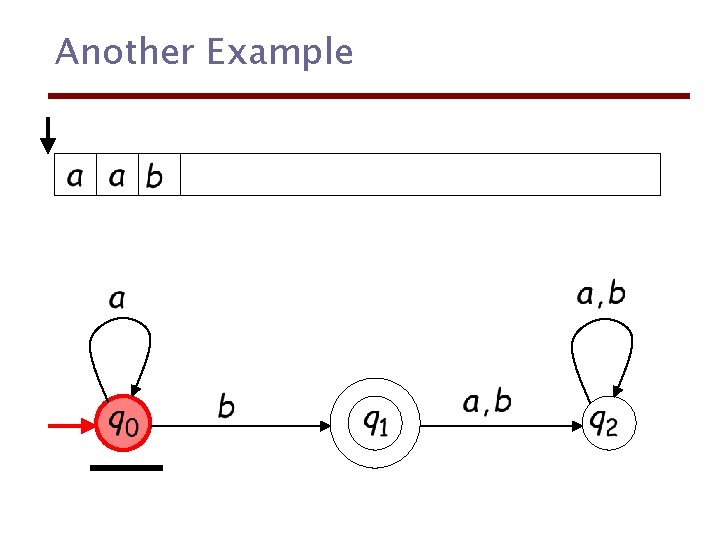
Another Example

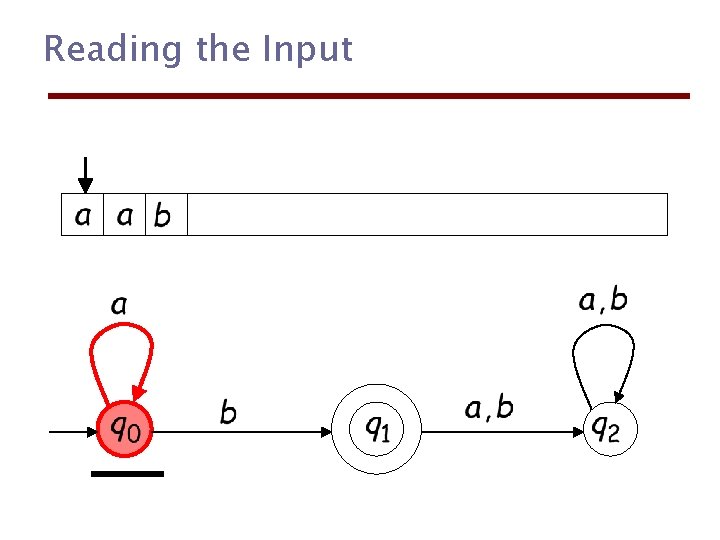
Reading the Input

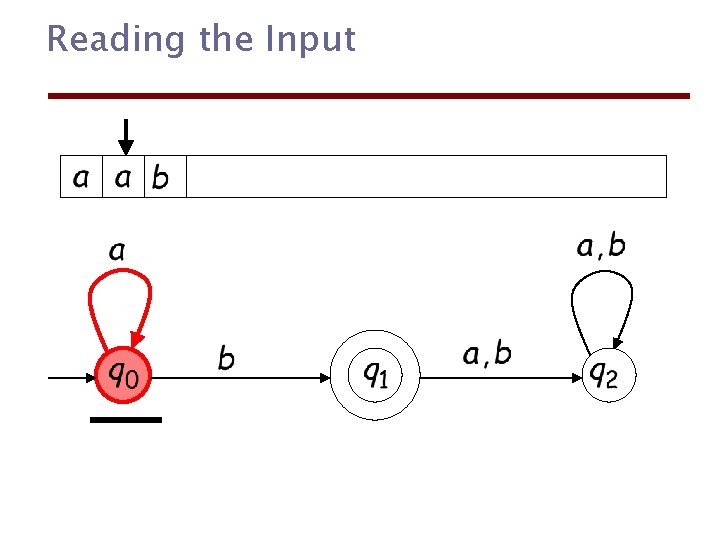
Reading the Input

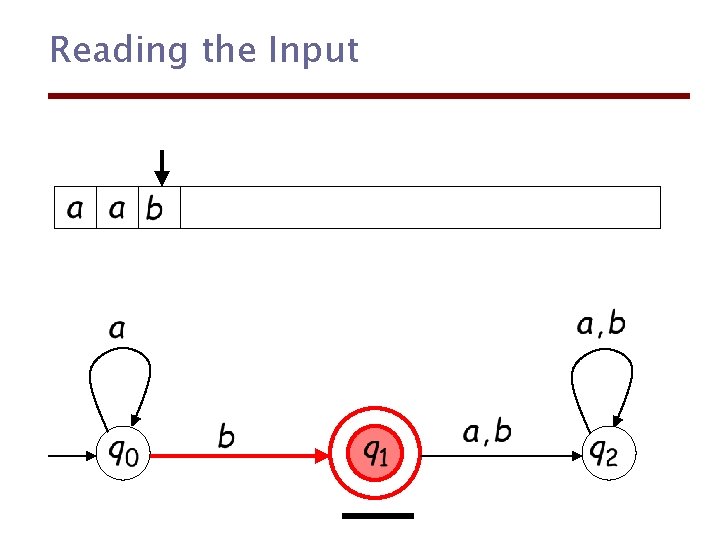
Reading the Input

Reading the Input finished Output: “accept”

Rejection

Reading the Input

Reading the Input

Reading the Input

Reading the Input finished Output: “reject”

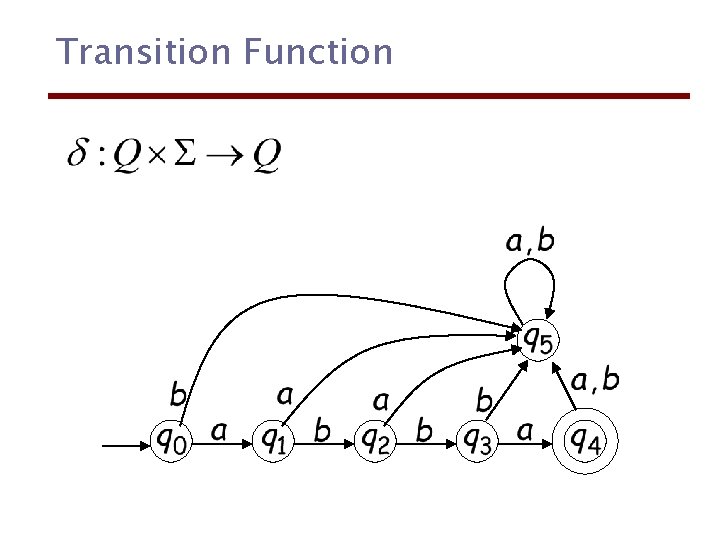
Formalities Deterministic Finite Accepter (DFA) : set of states : input alphabet : transition function : initial state : set of final states

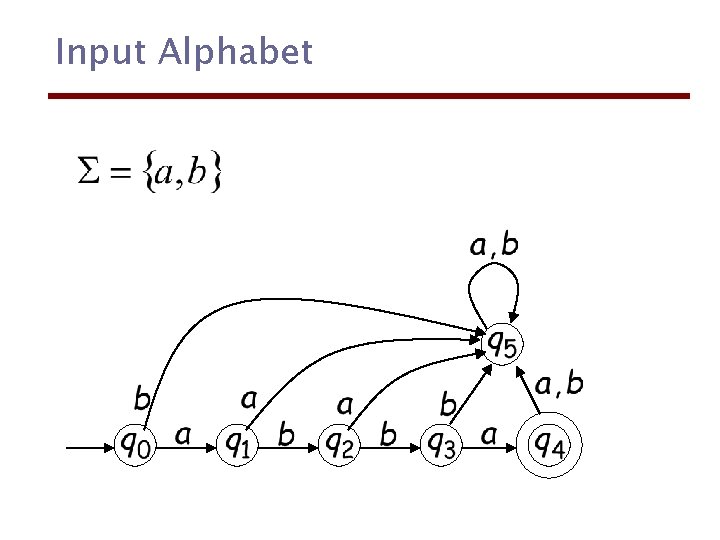
Input Alphabet

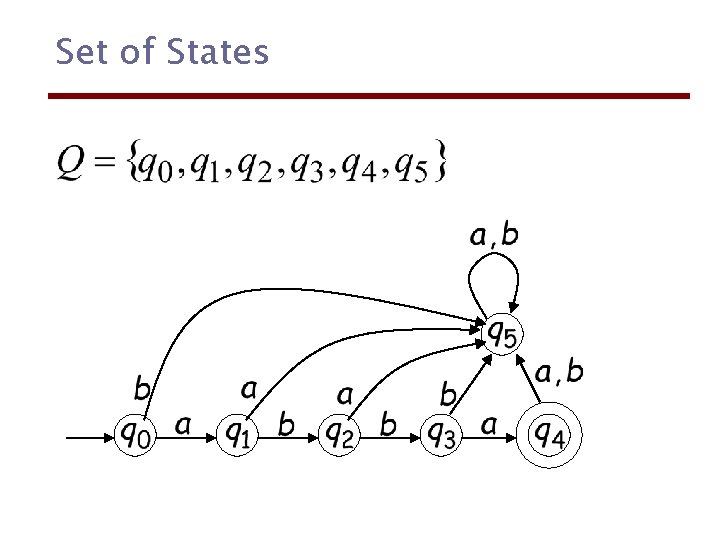
Set of States

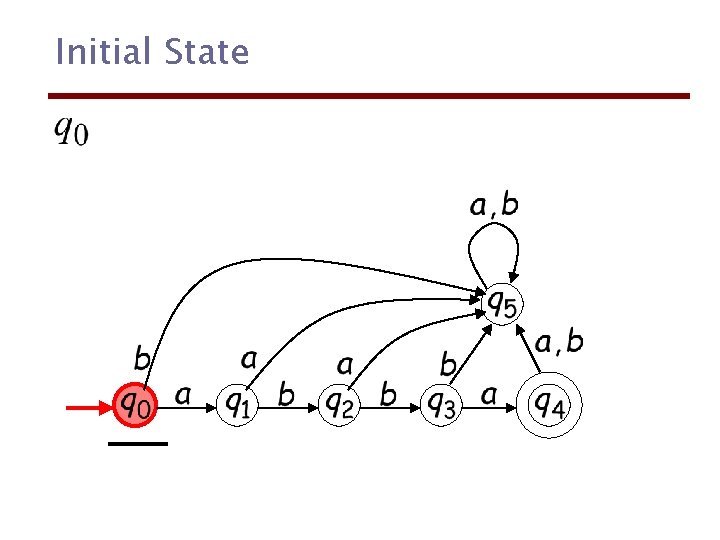
Initial State

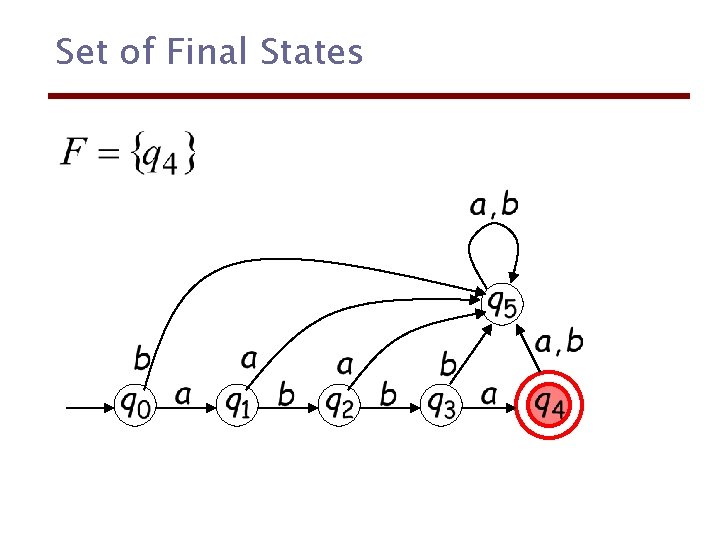
Set of Final States

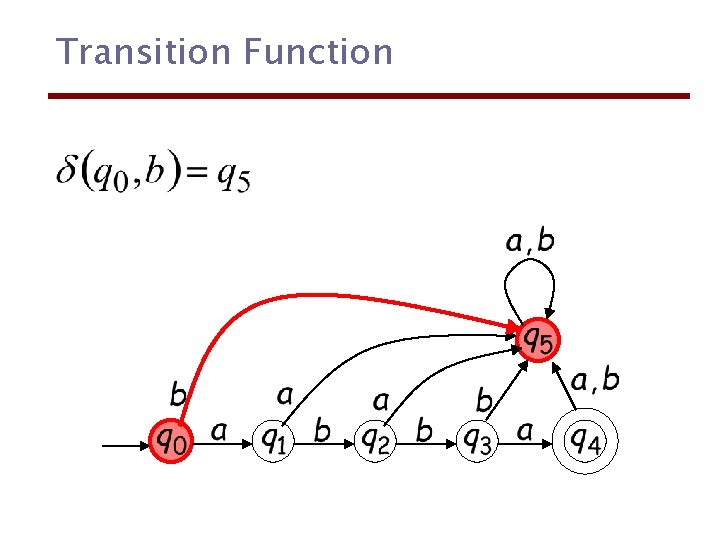
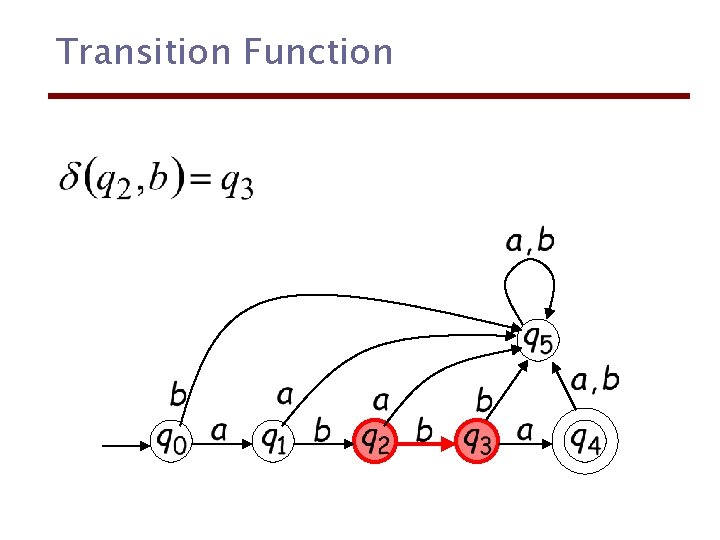
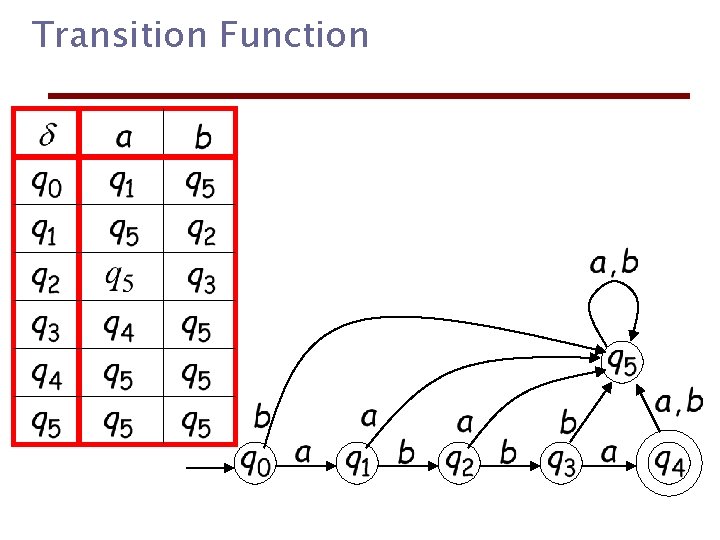
Transition Function

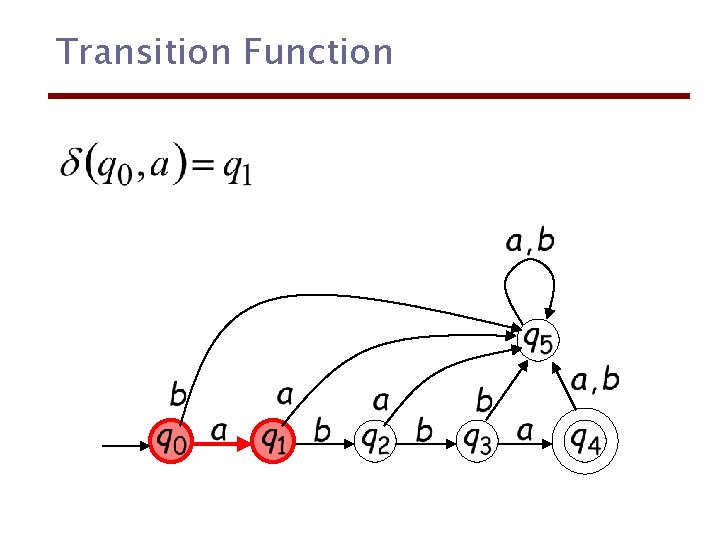
Transition Function

Transition Function

Transition Function

Transition Function

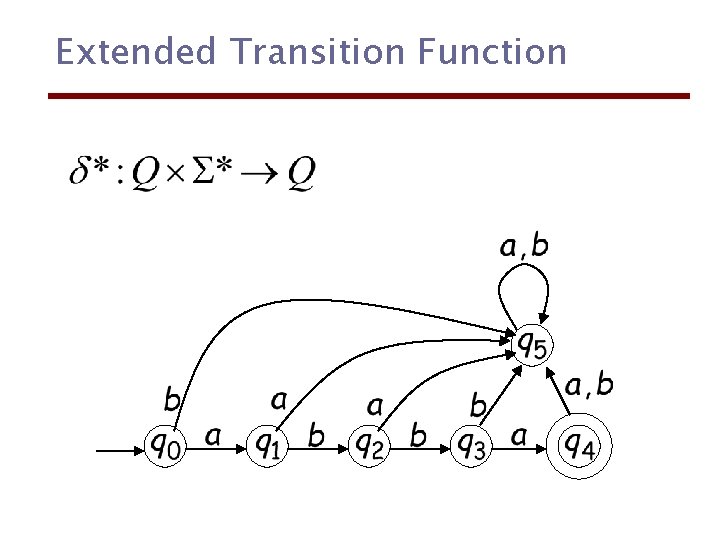
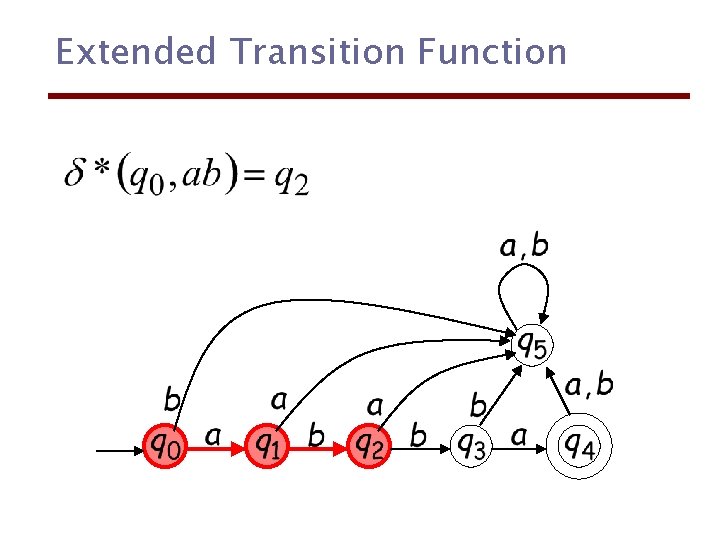
Extended Transition Function

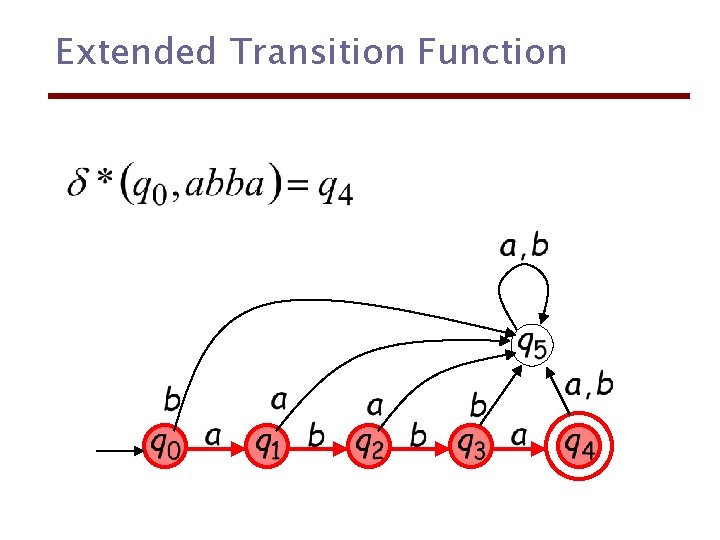
Extended Transition Function

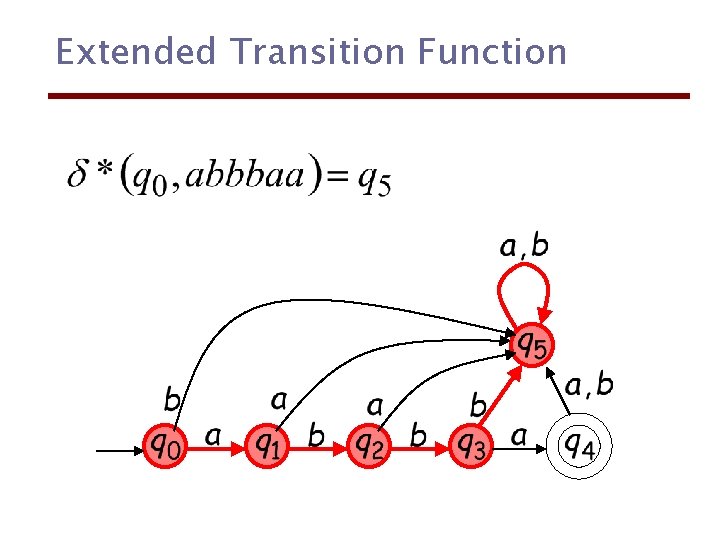
Extended Transition Function

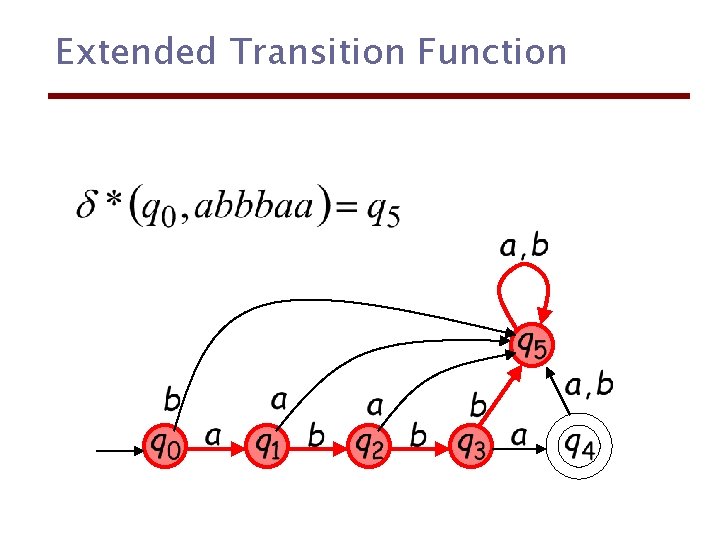
Extended Transition Function

Extended Transition Function

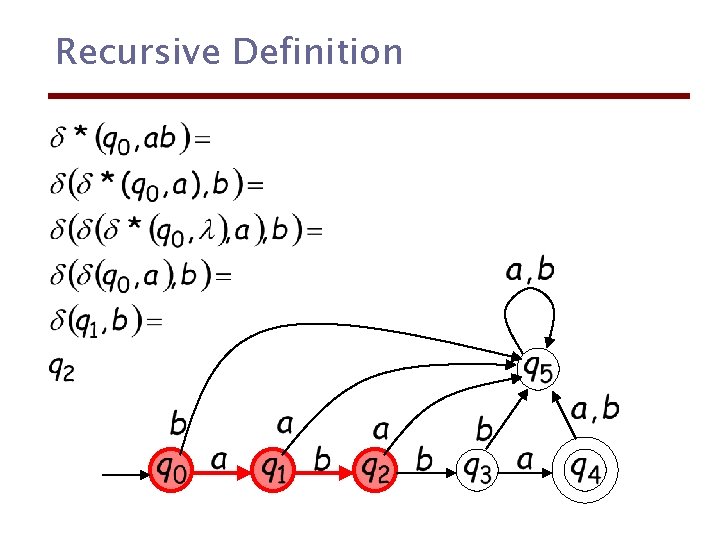
Recursive Definition

Recursive Definition

Languages Accepted by DFAs – The language contains – all input strings accepted by = { strings that drive to a final state}

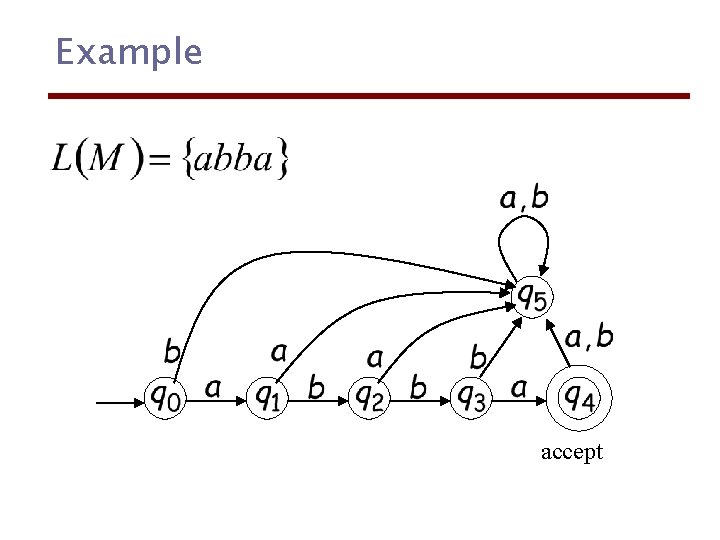
Example accept

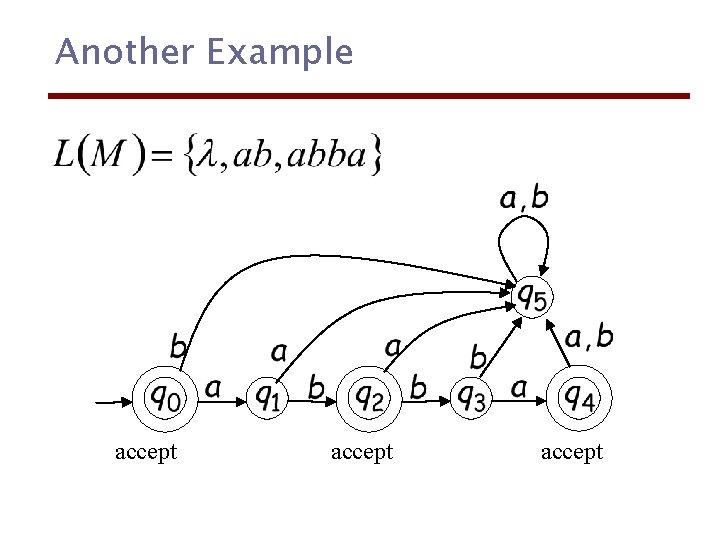
Another Example accept

Formally For a DFA Language accepted by :

Observation • Language rejected by :

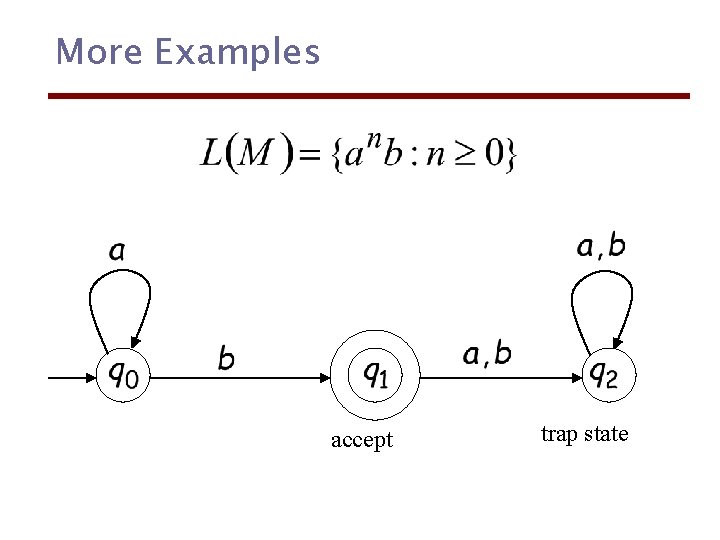
More Examples accept trap state

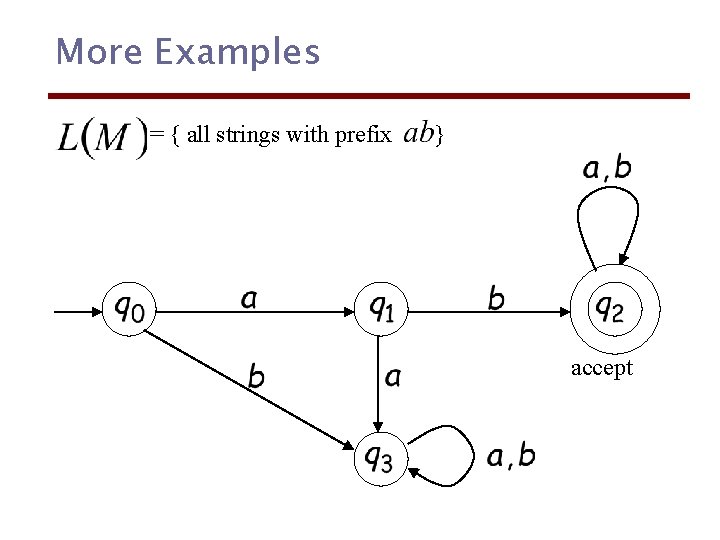
More Examples = { all strings with prefix } accept

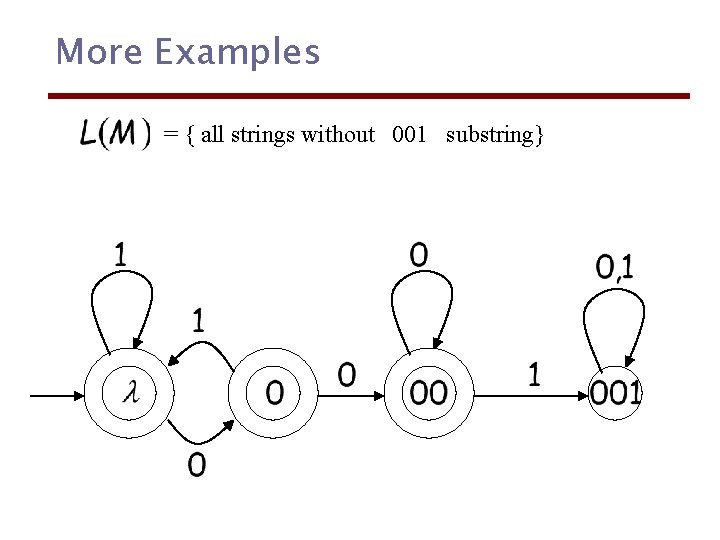
More Examples = { all strings without 001 substring}

Regular Languages • A language is regular if there is • a DFA such that • All regular languages form a language family –

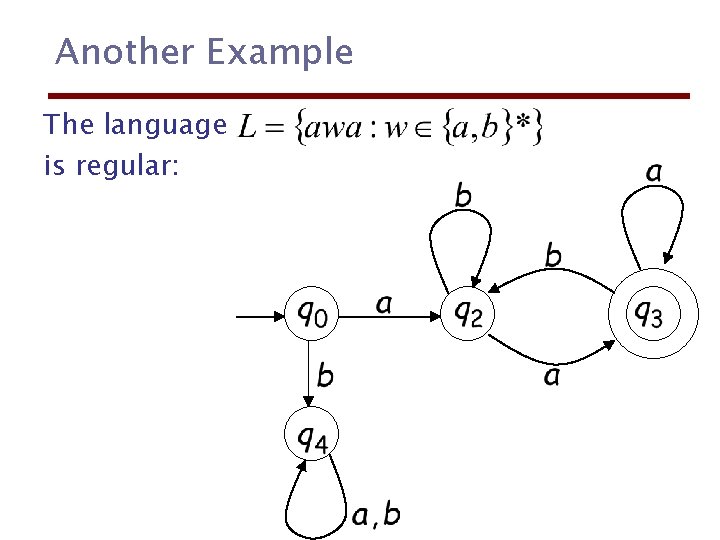
Another Example The language is regular:

Regular Languages There exist languages which are not Regular: Example: There is no DFA that accepts such a language