Mathematical Preliminaries 1 Mathematical Preliminaries Sets Functions Relations






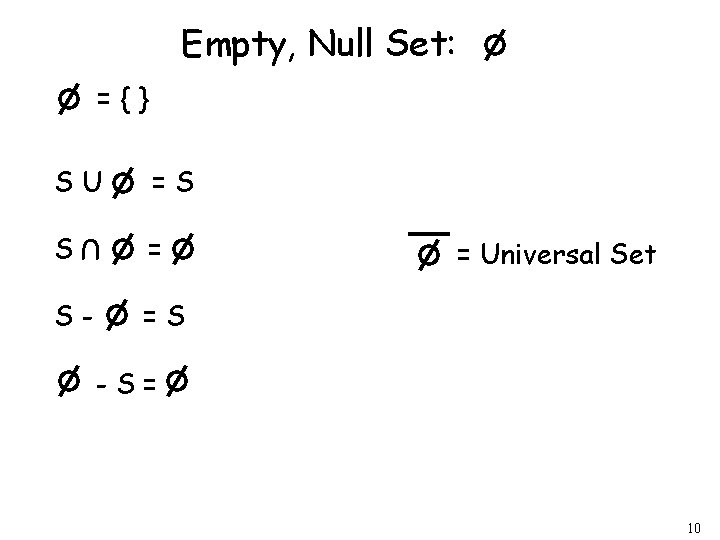














- Slides: 45

Mathematical Preliminaries 1

Mathematical Preliminaries • Sets • Functions • Relations • Graphs • Proof Techniques 2

SETS A set is a collection of elements We write 3

Set Representations C = { a, b, c, d, e, f, g, h, i, j, k } C = { a, b, …, k } finite set S = { 2, 4, 6, … } infinite set S = { j : j > 0, and j = 2 k for some k>0 } S = { j : j is nonnegative and even } 4

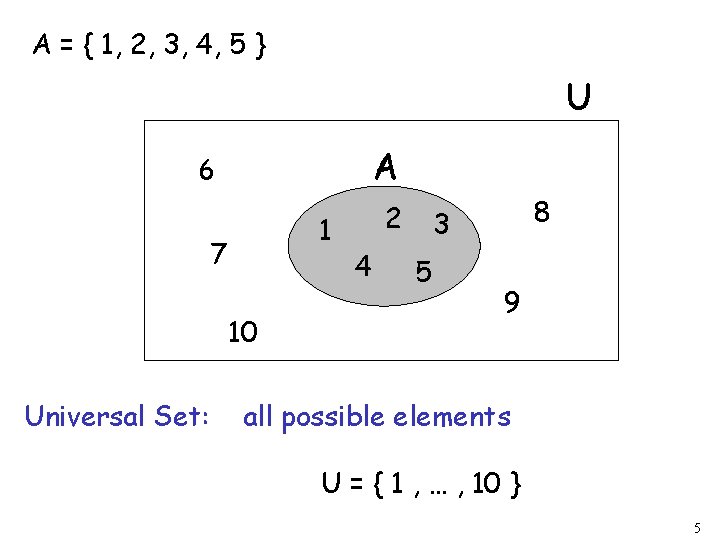
A = { 1, 2, 3, 4, 5 } U A 6 1 7 10 Universal Set: 2 4 8 3 5 9 all possible elements U = { 1 , … , 10 } 5

Set Operations A = { 1, 2, 3 } B = { 2, 3, 4, 5} B A • Union A U B = { 1, 2, 3, 4, 5 } 2 3 1 4 5 • Intersection U A B = { 2, 3 } 2 3 • Difference A-B={1} B - A = { 4, 5 } 1 Venn diagrams 6

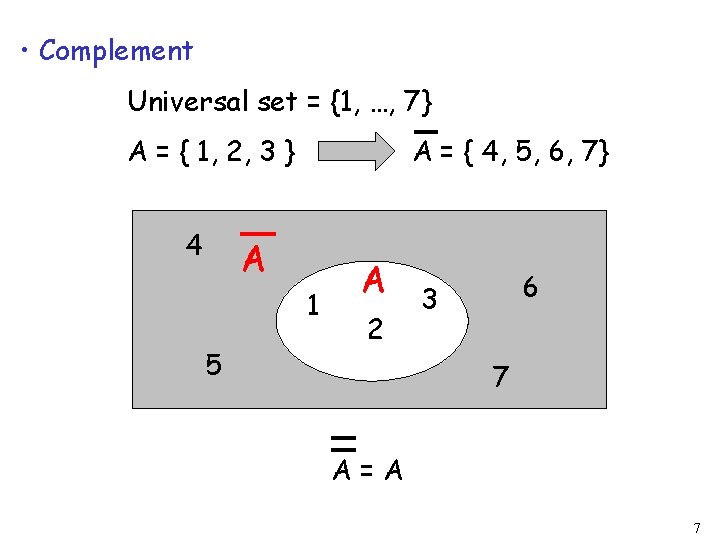
• Complement Universal set = {1, …, 7} A = { 1, 2, 3 } 4 A = { 4, 5, 6, 7} A 1 5 A 2 6 3 7 A=A 7

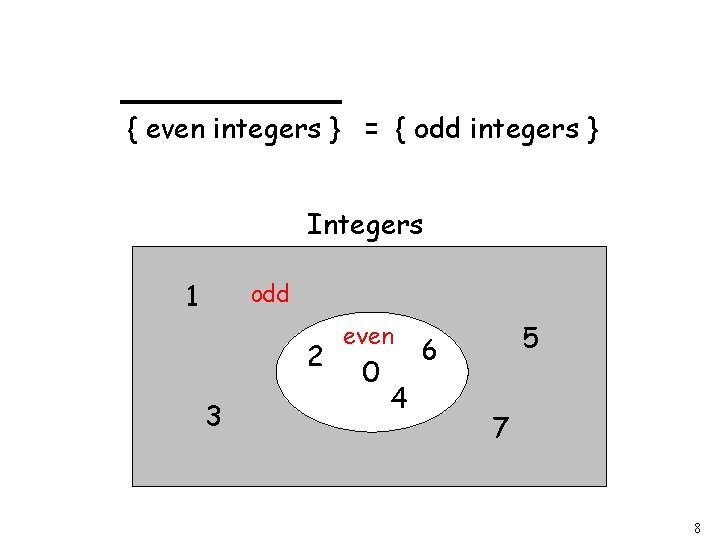
{ even integers } = { odd integers } Integers 1 odd 2 3 even 0 4 5 6 7 8

De. Morgan’s Laws U AUB=A B B=AUB 9
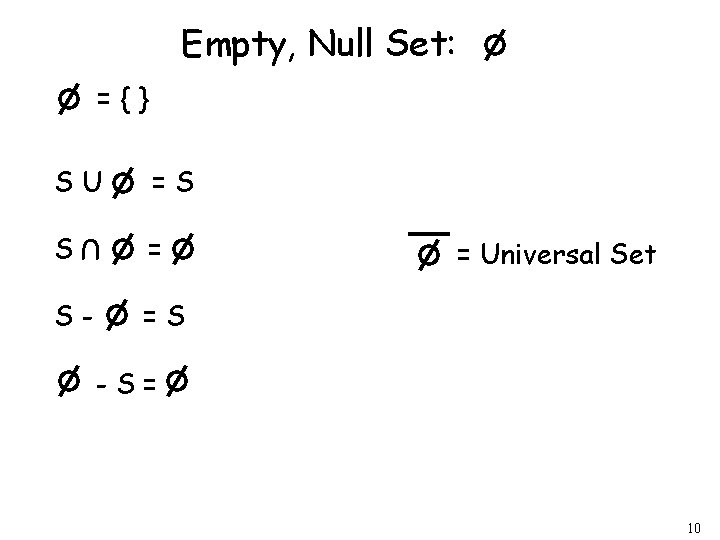
Empty, Null Set: ={} SU =S S = U S- = Universal Set =S -S= 10

Subset A = { 1, 2, 3} B = { 1, 2, 3, 4, 5 } B U Proper Subset: A U A B B A 11

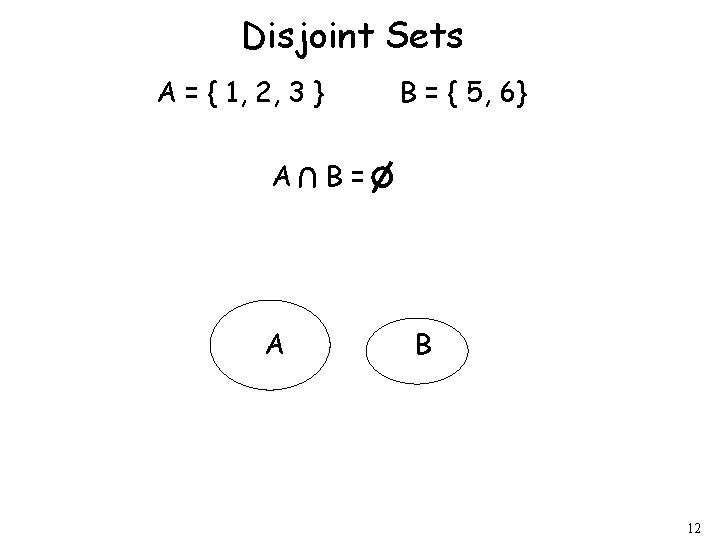
Disjoint Sets A = { 1, 2, 3 } A U A B = { 5, 6} B= B 12

Set Cardinality • For finite sets A = { 2, 5, 7 } |A| = 3 (set size) 13

Powersets A powerset is a set of sets S = { a, b, c } Powerset of S = the set of all the subsets of S 2 S = { , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} } Observation: | 2 S | = 2|S| ( 8 = 23 ) 14

Cartesian Product A = { 2, 4 } B = { 2, 3, 5 } A X B = { (2, 2), (2, 3), (2, 5), ( 4, 2), (4, 3), (4, 5) } |A X B| = |A| |B| Generalizes to more than two sets AXBX…XZ 15

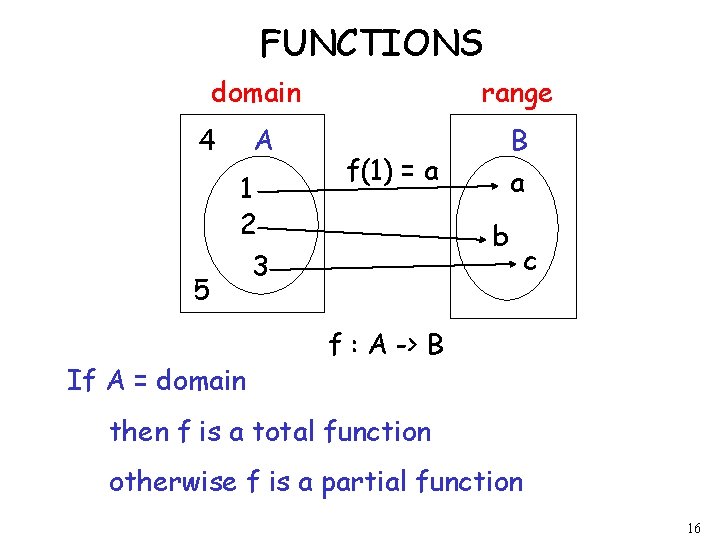
FUNCTIONS domain 4 5 A 1 2 3 If A = domain range B f(1) = a a b c f : A -> B then f is a total function otherwise f is a partial function 16

RELATIONS R = {(x 1, y 1), (x 2, y 2), (x 3, y 3), …} x i R yi e. g. if R = ‘>’: 2 > 1, 3 > 2, 3 > 1 17

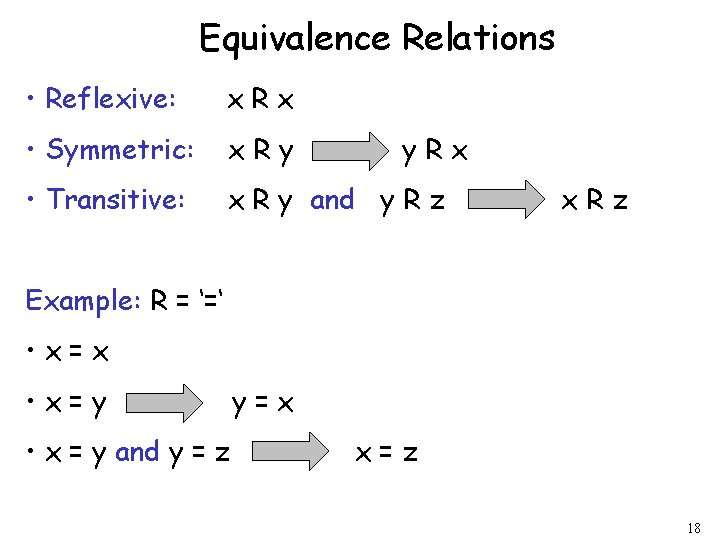
Equivalence Relations • Reflexive: x. Rx • Symmetric: x. Ry • Transitive: x R y and y R z y. Rx x. Rz Example: R = ‘=‘ • x=x • x=y • x = y and y = z y=x x=z 18

Equivalence Classes For equivalence relation R equivalence class of x = {y : x R y} Example: R = { (1, 1), (2, 2), (1, 2), (2, 1), (3, 3), (4, 4), (3, 4), (4, 3) } Equivalence class of 1 = {1, 2} Equivalence class of 3 = {3, 4} 19

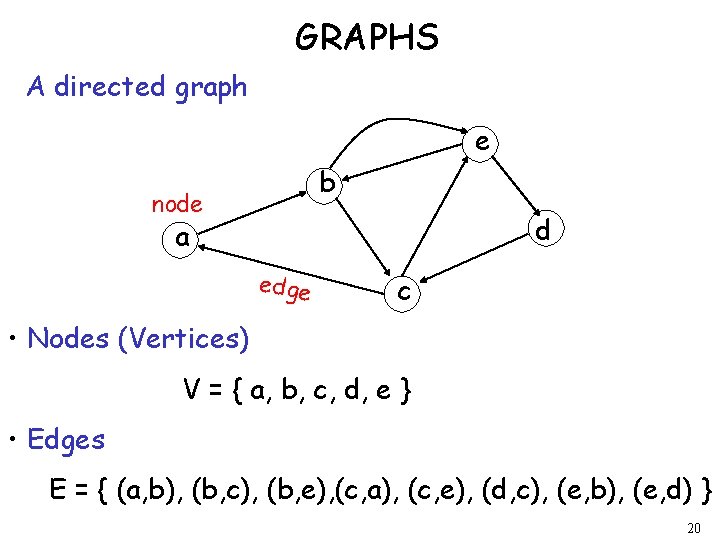
GRAPHS A directed graph e b node d a edge c • Nodes (Vertices) V = { a, b, c, d, e } • Edges E = { (a, b), (b, c), (b, e), (c, a), (c, e), (d, c), (e, b), (e, d) } 20

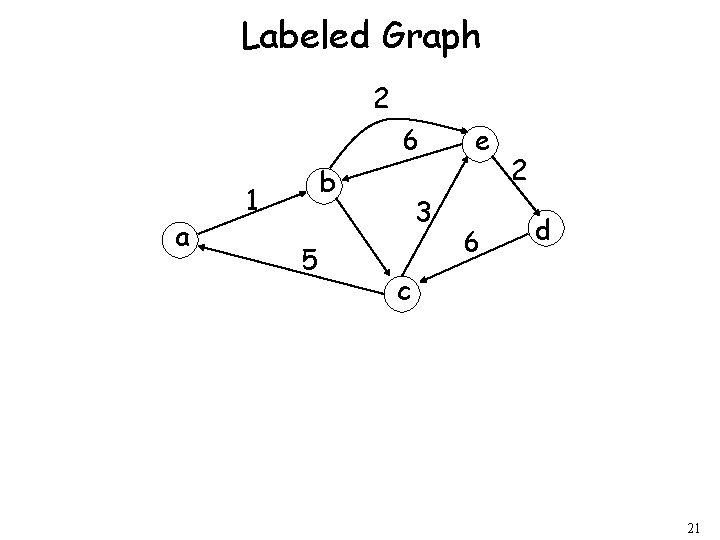
Labeled Graph 2 6 a b 1 5 3 e 6 2 d c 21

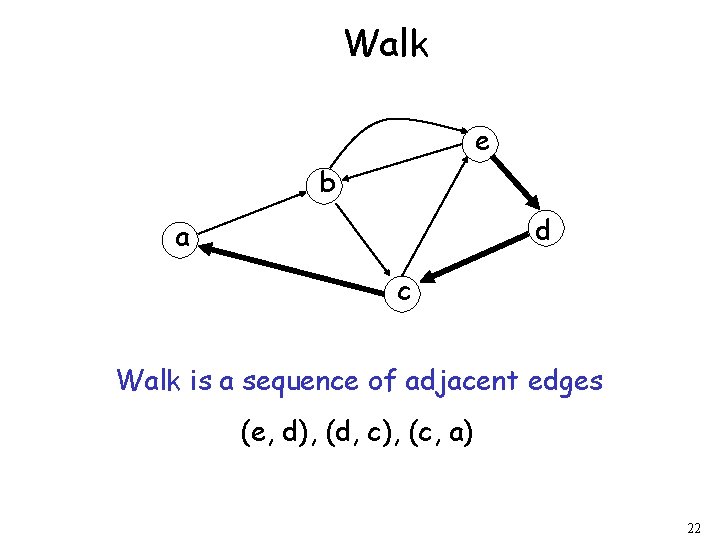
Walk e b d a c Walk is a sequence of adjacent edges (e, d), (d, c), (c, a) 22

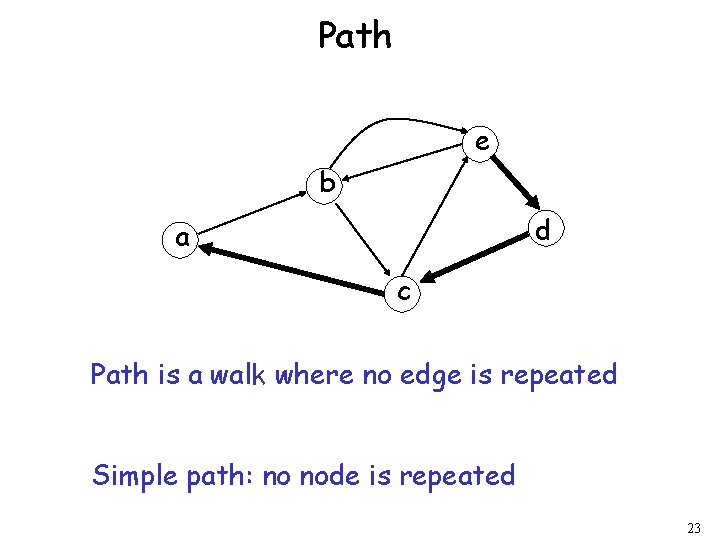
Path e b d a c Path is a walk where no edge is repeated Simple path: no node is repeated 23

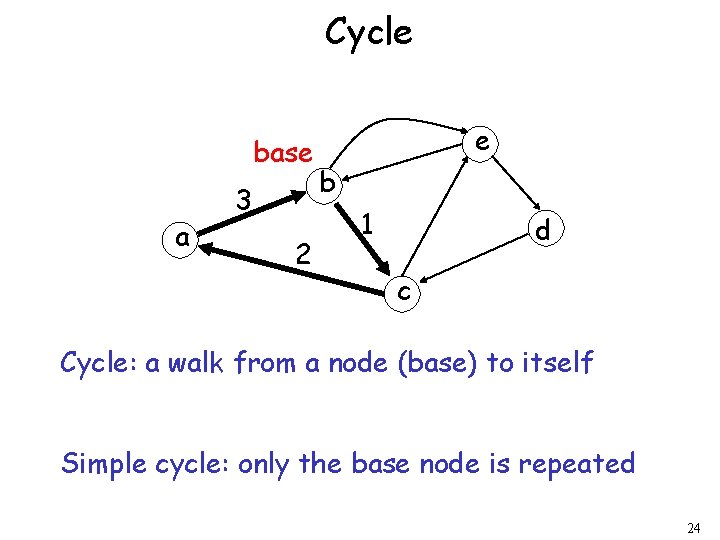
Cycle base a 3 2 e b 1 d c Cycle: a walk from a node (base) to itself Simple cycle: only the base node is repeated 24

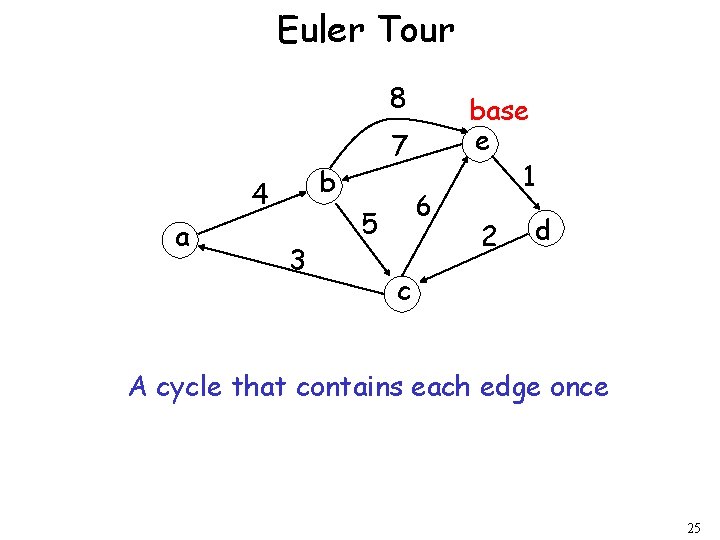
Euler Tour 8 b 4 a 7 3 6 5 base e 1 2 d c A cycle that contains each edge once 25

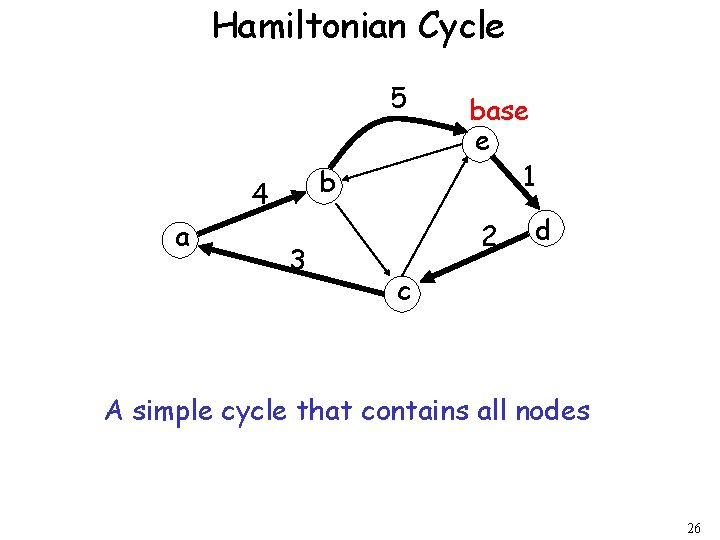
Hamiltonian Cycle 5 b 4 a 3 base e 1 2 d c A simple cycle that contains all nodes 26

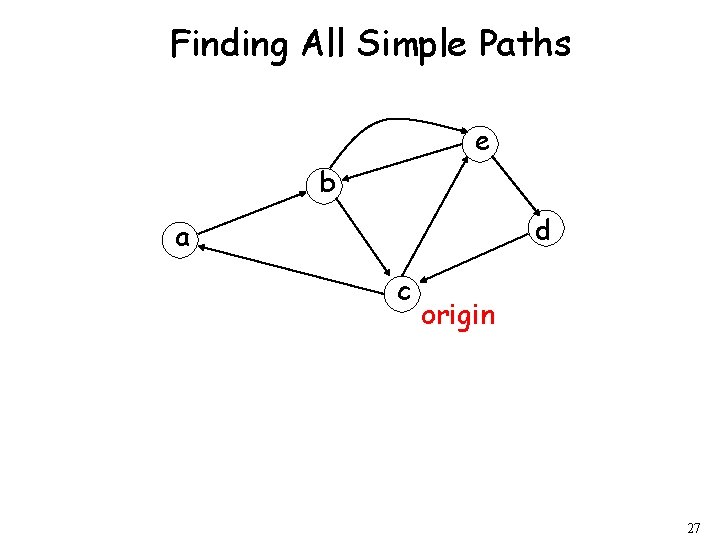
Finding All Simple Paths e b d a c origin 27

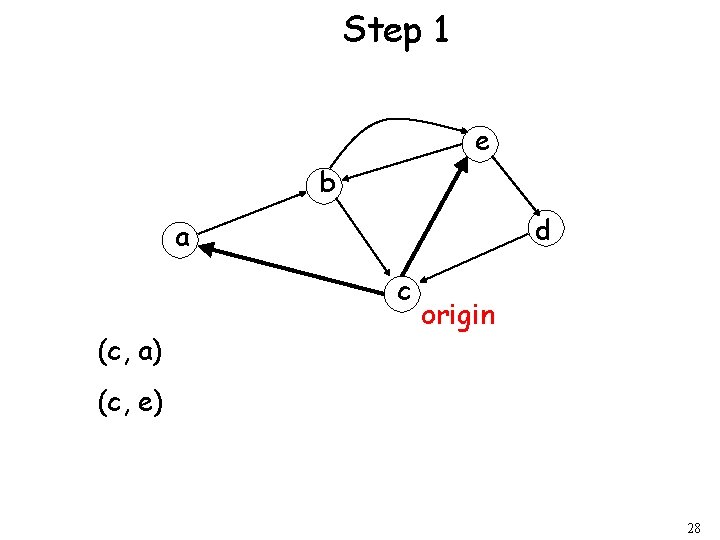
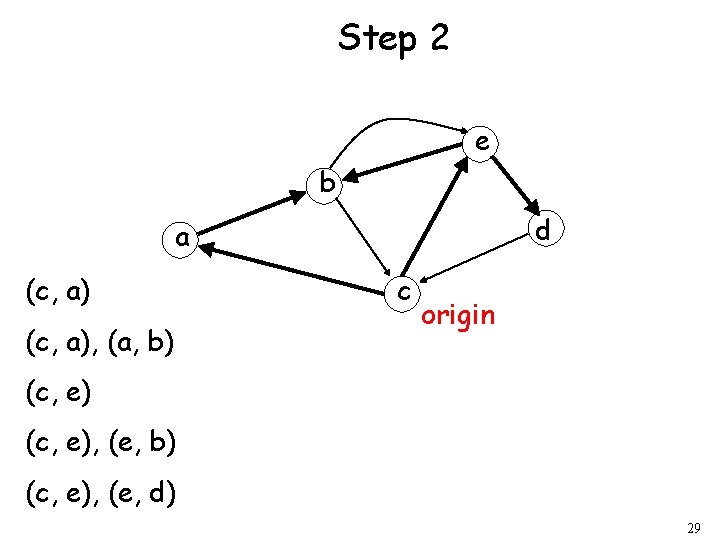
Step 1 e b d a c (c, a) origin (c, e) 28

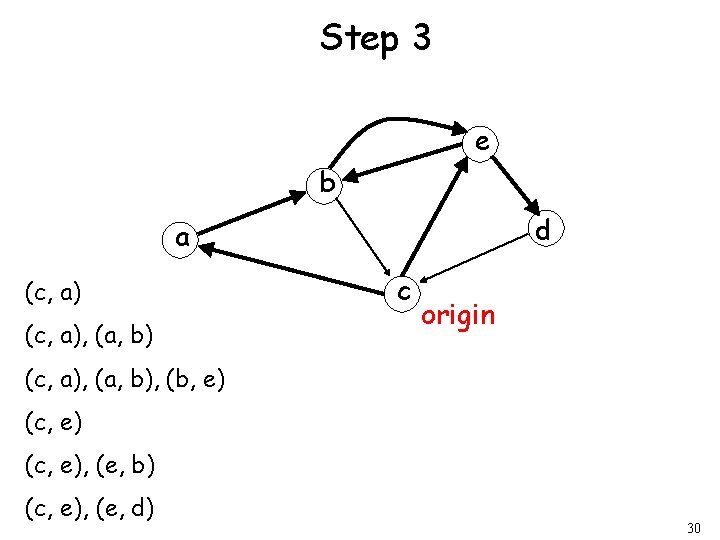
Step 2 e b d a (c, a), (a, b) c origin (c, e), (e, b) (c, e), (e, d) 29

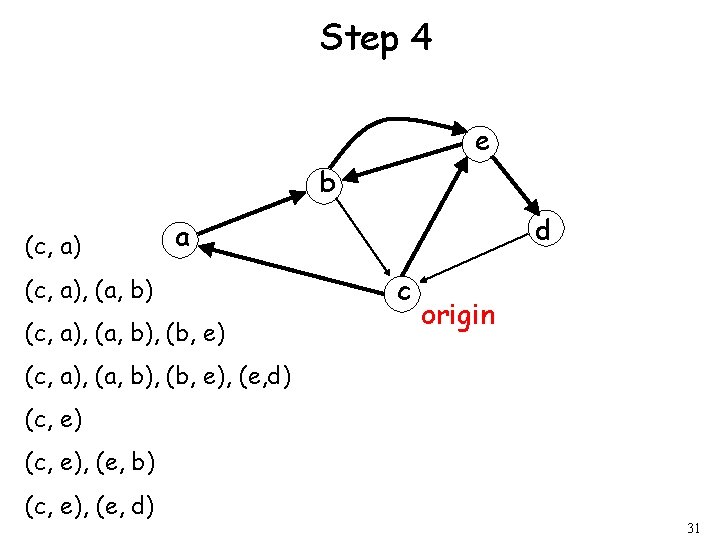
Step 3 e b d a (c, a), (a, b) c origin (c, a), (a, b), (b, e) (c, e), (e, b) (c, e), (e, d) 30

Step 4 e b (c, a) d a (c, a), (a, b), (b, e) c origin (c, a), (a, b), (b, e), (e, d) (c, e), (e, b) (c, e), (e, d) 31

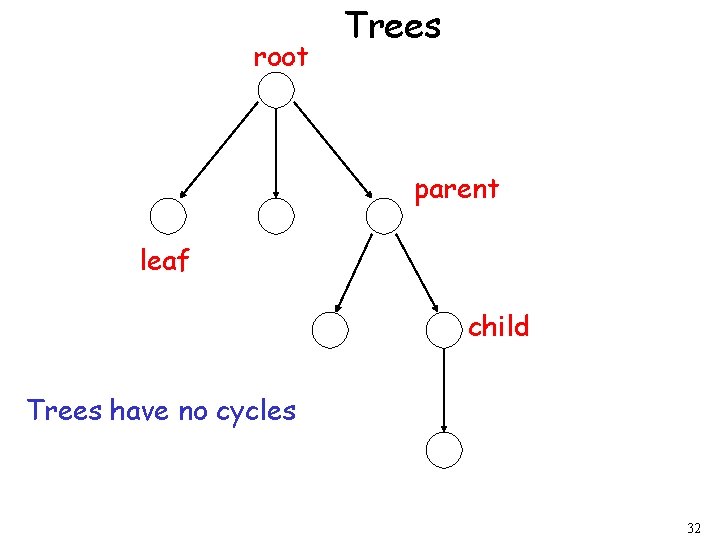
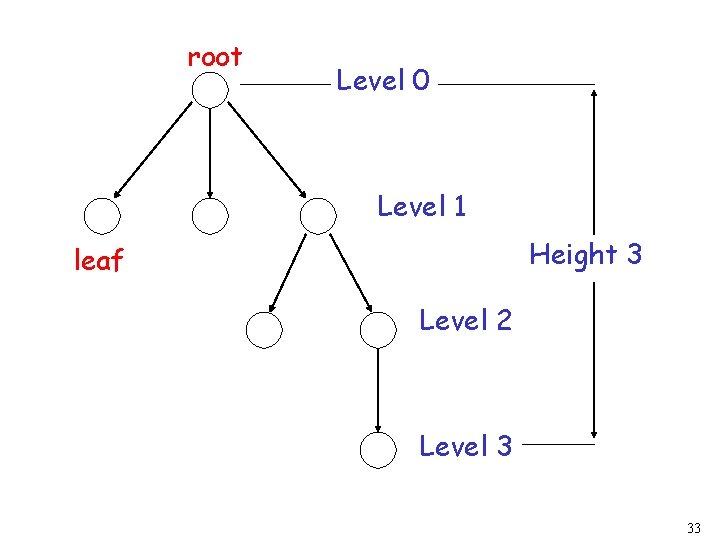
root Trees parent leaf child Trees have no cycles 32

root Level 0 Level 1 Height 3 leaf Level 2 Level 3 33

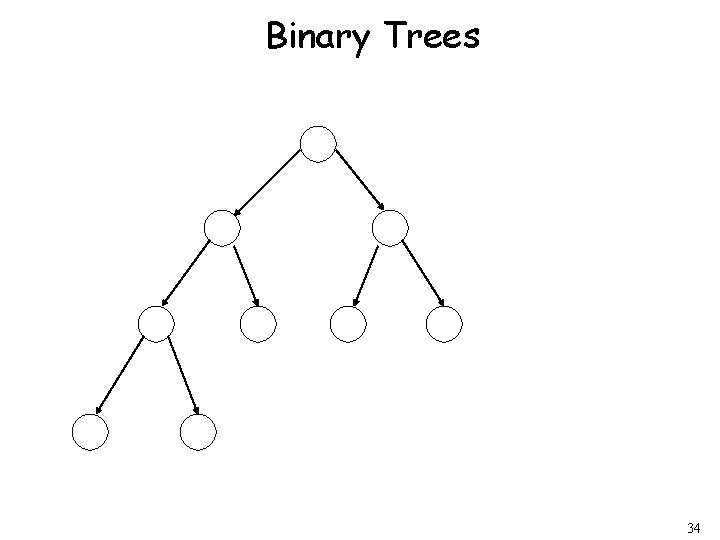
Binary Trees 34

PROOF TECHNIQUES • Proof by induction • Proof by contradiction 35

Induction We have statements P 1, P 2, P 3, … If we know • for some b that P 1, P 2, …, Pb are true • for any k >= b that P 1, P 2, …, Pk imply Pk+1 Then Every Pi is true 36

Proof by Induction • Inductive basis Find P 1, P 2, …, Pb which are true • Inductive hypothesis Let’s assume P 1, P 2, …, Pk are true, for any k >= b • Inductive step Show that Pk+1 is true 37

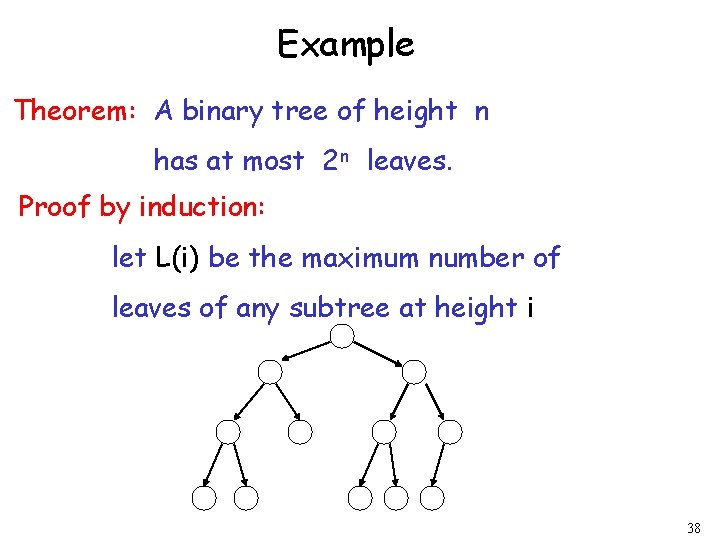
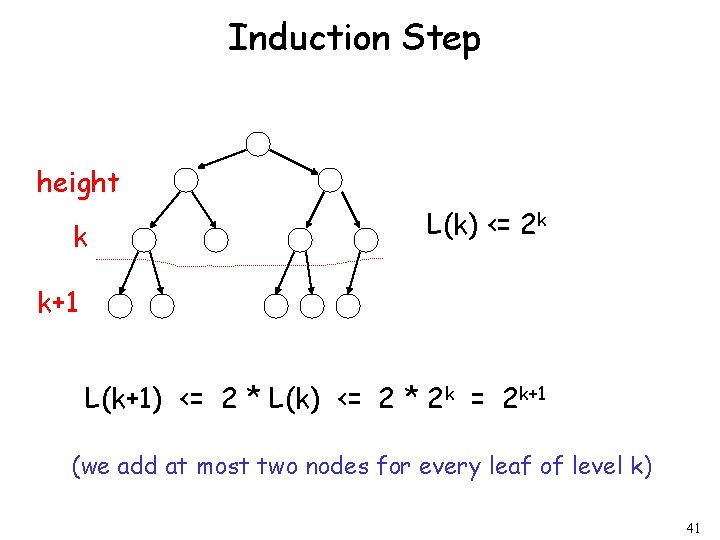
Example Theorem: A binary tree of height n has at most 2 n leaves. Proof by induction: let L(i) be the maximum number of leaves of any subtree at height i 38

We want to show: L(i) <= 2 i • Inductive basis L(0) = 1 (the root node) • Inductive hypothesis Let’s assume L(i) <= 2 i for all i = 0, 1, …, k • Induction step we need to show that L(k + 1) <= 2 k+1 39

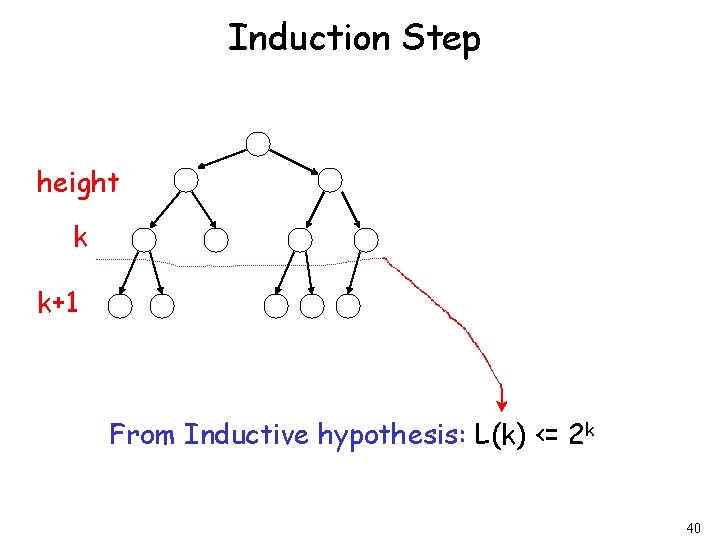
Induction Step height k k+1 From Inductive hypothesis: L(k) <= 2 k 40

Induction Step height k L(k) <= 2 k k+1 L(k+1) <= 2 * L(k) <= 2 * 2 k = 2 k+1 (we add at most two nodes for every leaf of level k) 41

Remark Recursion is another thing Example of recursive function: f(n) = f(n-1) + f(n-2) f(0) = 1, f(1) = 1 42

Proof by Contradiction We want to prove that a statement P is true • we assume that P is false • then we arrive at an incorrect conclusion • therefore, statement P must be true 43

Example Theorem: is not rational Proof: Assume by contradiction that it is rational = n/m n and m have no common factors We will show that this is impossible 44

= n/m Therefore, 2 m 2 = 4 k 2 n 2 2 m 2 = n 2 is even m 2 = 2 k 2 n is even n=2 k m is even m=2 p Thus, m and n have common factor 2 Contradiction! 45