MATEMTICA MATEMTICA PARA COMPREENDER O MUNDO Ktia Stocco

MATEMÁTICA

MATEMÁTICA PARA COMPREENDER O MUNDO Kátia Stocco Smole; Maria Ignez Diniz 1º ano ensino médio

Unidade 4 – Funções e trigonometria do triângulo NESSA UNIDADE: • Operações entre funções • Composição de funções • Função injetora, sobrejetora e bijetora • Inversão de funções • Funções definidas por partes • Função modular • Trigonometria em triângulos retângulos e o Teorema de Pitágoras • Teorema de Tales • Relações trigonométricas em um triângulo retângulo • Tabela trigonométrica • Relações entre seno, cosseno e tangente • Relações trigonométricas em triângulos quaisquer – Lei dos senos e lei dos cossenos • Teorema da área MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre

CAPÍTULO 9 – OPERAÇÕES ENTRE FUNÇÕES AS QUATRO OPERAÇÕES BÁSICAS ENTRE NÚMEROS E NOVAS FUNÇÕES MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre

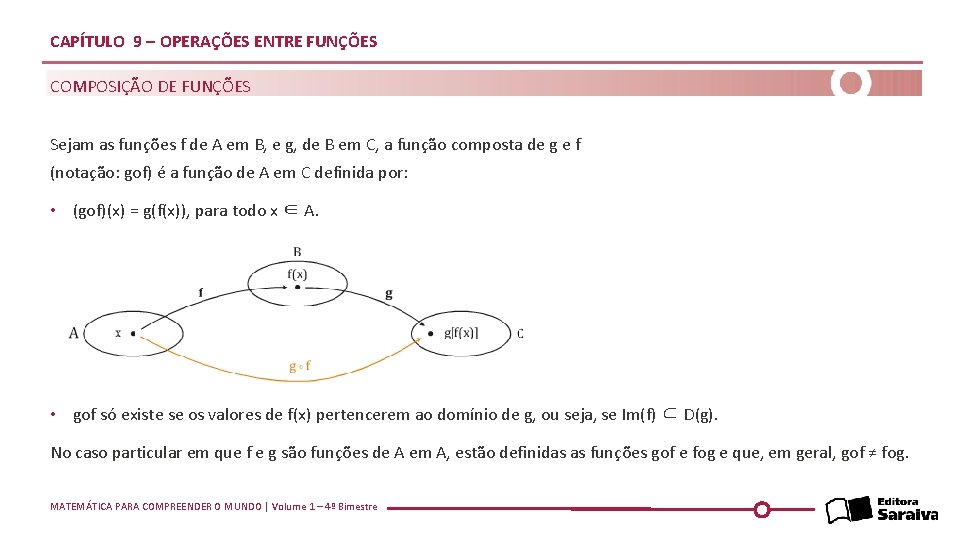
CAPÍTULO 9 – OPERAÇÕES ENTRE FUNÇÕES COMPOSIÇÃO DE FUNÇÕES Sejam as funções f de A em B, e g, de B em C, a função composta de g e f (notação: gof) é a função de A em C definida por: • (gof)(x) = g(f(x)), para todo x ∈ A. • gof só existe se os valores de f(x) pertencerem ao domínio de g, ou seja, se Im(f) ⊂ D(g). No caso particular em que f e g são funções de A em A, estão definidas as funções gof e fog e que, em geral, gof ≠ fog. MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre

CAPÍTULO 9 – OPERAÇÕES ENTRE FUNÇÕES FUNÇÃO INJETORA, FUNÇÃO SOBREJETORA E FUNÇÃO BIJETORA Uma função f, de A em B, é injetora (ou uma injeção) se quaisquer que sejam x 1 ∈ A e x 2 ∈ A, x 1 ≠ x 2, temos f(x 1) ≠ f(x 2). Uma função g, de C em D, é sobrejetora (ou uma sobrejeção) se CD(g) = Im(g). Seja uma função h de H em I, h é bijetora (ou uma bijeção) se h é injetora e h é sobrejetora. MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre

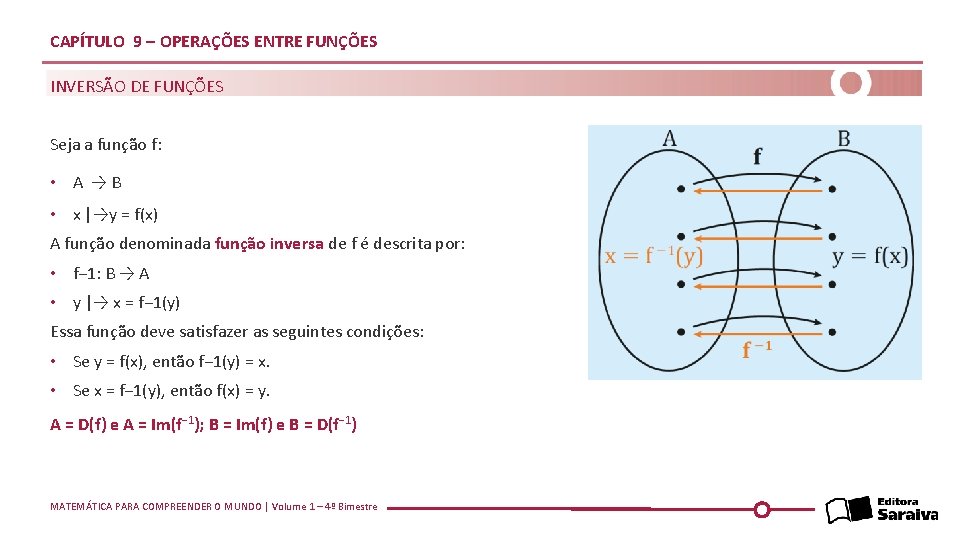
CAPÍTULO 9 – OPERAÇÕES ENTRE FUNÇÕES INVERSÃO DE FUNÇÕES Seja a função f: • A → B • x |→y = f(x) A função denominada função inversa de f é descrita por: • f− 1: B → A • y |→ x = f− 1(y) Essa função deve satisfazer as seguintes condições: • Se y = f(x), então f− 1(y) = x. • Se x = f− 1(y), então f(x) = y. A = D(f) e A = Im(f− 1); B = Im(f) e B = D(f− 1) MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre

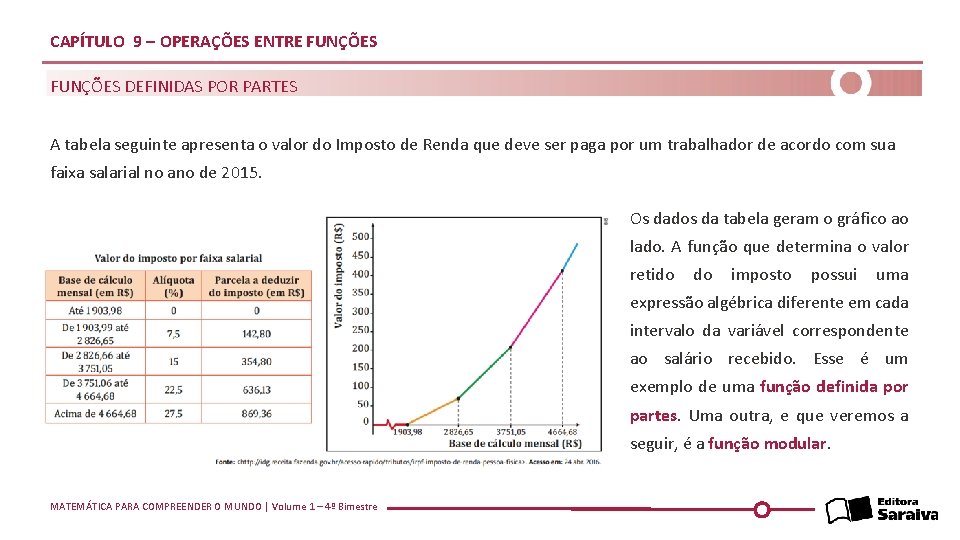
CAPÍTULO 9 – OPERAÇÕES ENTRE FUNÇÕES DEFINIDAS POR PARTES A tabela seguinte apresenta o valor do Imposto de Renda que deve ser paga por um trabalhador de acordo com sua faixa salarial no ano de 2015. Os dados da tabela geram o gráfico ao lado. A função que determina o valor retido do imposto possui uma expressão algébrica diferente em cada intervalo da variável correspondente ao salário recebido. Esse é um exemplo de uma função definida por partes. Uma outra, e que veremos a seguir, é a função modular. MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre

CAPÍTULO 9 – OPERAÇÕES ENTRE FUNÇÕES MÓDULO DE UM NÚMERO REAL Propriedades do módulo de um número real De forma geral, sendo a > 0, temos: 1) |x| = a ⇔ x = a ou x = − a 2) |x| < a ⇔ − a < x < a 3) |x| > a ⇔ x < − a ou x > a MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre

CAPÍTULO 9 – OPERAÇÕES ENTRE FUNÇÕES FUNÇÃO MODULAR A função f, de ℝ → ℝ, que a todo número x associa o seu módulo é denominada função modular. • f: ℝ → ℝ • x |→y = |x| Gráfico cartesiano da função modular f: ℝ → ℝ, f(x) = |x| MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre

CAPÍTULO 10 – TRIGONOMETRIA DO TRI NGULO RET NGULO É todo triângulo que tem um ângulo reto. Na figura seguinte, o ângulo B C é reto. Diz-se nesse caso que o triângulo ABC é reto em A, Teorema de Pitágoras Em todo triângulo retângulo, a soma dos quadrados das medidas dos catetos é igual ao quadrado da medida da hipotenusa. Na figura, b e c são os catetos e a (lado oposto ao ângulo reto) é a hipotenusa. MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre a² = b² + c²

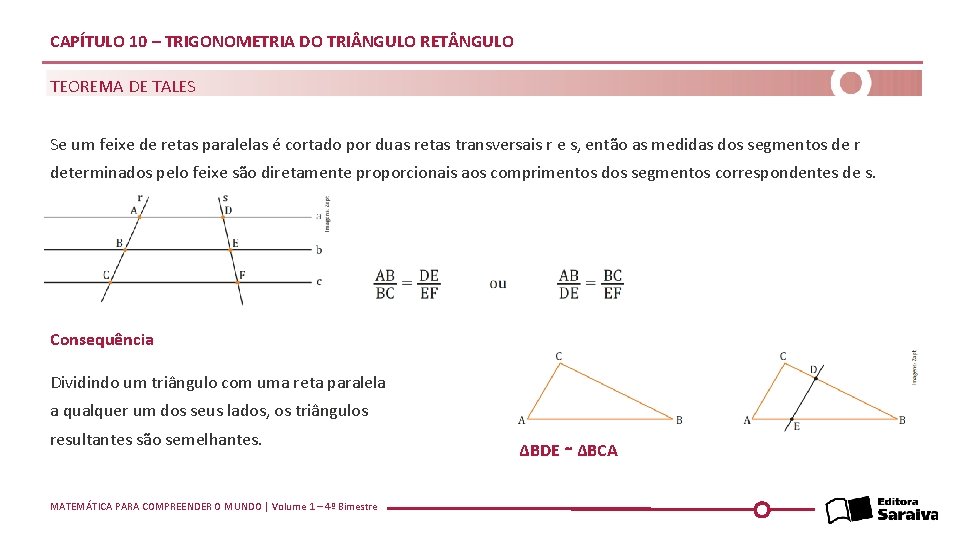
CAPÍTULO 10 – TRIGONOMETRIA DO TRI NGULO RET NGULO TEOREMA DE TALES Se um feixe de retas paralelas é cortado por duas retas transversais r e s, então as medidas dos segmentos de r determinados pelo feixe são diretamente proporcionais aos comprimentos dos segmentos correspondentes de s. Consequência Dividindo um triângulo com uma reta paralela a qualquer um dos seus lados, os triângulos resultantes são semelhantes. MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre ΔBDE ∼ ΔBCA

CAPÍTULO 10 – TRIGONOMETRIA DO TRI NGULO RET NGULO RELAÇÕES TRIGONOMÉTRICAS EM UM TRI NGULO RET NGULO MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre

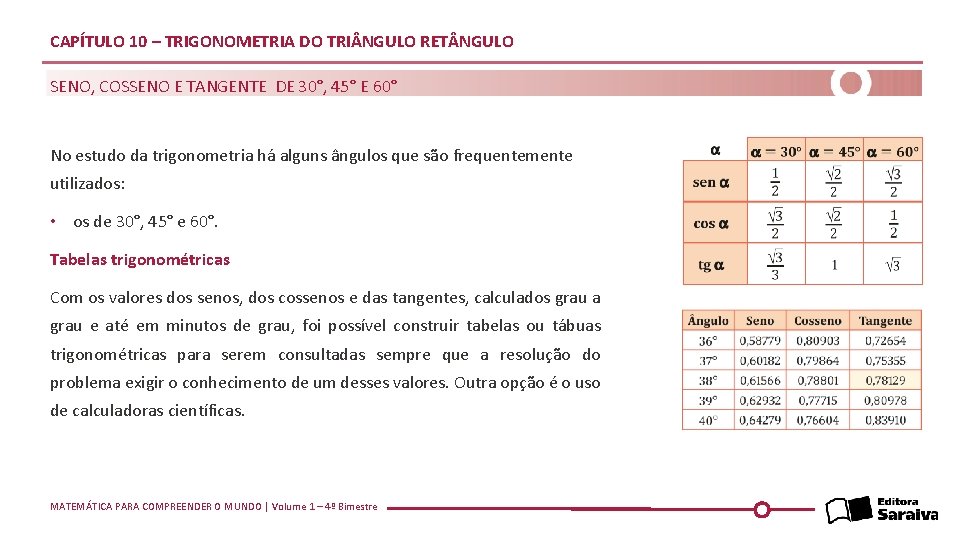
CAPÍTULO 10 – TRIGONOMETRIA DO TRI NGULO RET NGULO SENO, COSSENO E TANGENTE DE 30°, 45° E 60° No estudo da trigonometria há alguns ângulos que são frequentemente utilizados: • os de 30°, 45° e 60°. Tabelas trigonométricas Com os valores dos senos, dos cossenos e das tangentes, calculados grau a grau e até em minutos de grau, foi possível construir tabelas ou tábuas trigonométricas para serem consultadas sempre que a resolução do problema exigir o conhecimento de um desses valores. Outra opção é o uso de calculadoras científicas. MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre

CAPÍTULO 10 – TRIGONOMETRIA DO TRI NGULO RET NGULO RELAÇÕES ENTRE SENO, COSSENO E TANGENTE Como as razões trigonométricas seno, cosseno e tangente se referem a um mesmo triângulo retângulo, elas possuem algumas relações entre si. A soma dos quadrados do seno e do cosseno de um ângulo agudo é igual a 1. • sen 2α + cos 2α = 1 O seno de um ângulo agudo é igual ao cosseno do complemento desse ângulo e vice-versa. • sen α = cos (90° − α) e cos α = sen (90° − α) MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre

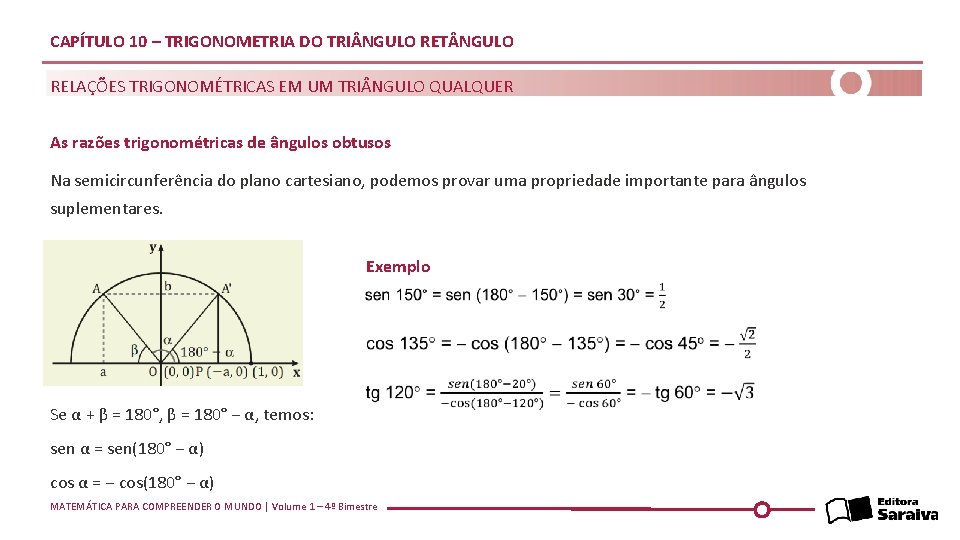
CAPÍTULO 10 – TRIGONOMETRIA DO TRI NGULO RET NGULO RELAÇÕES TRIGONOMÉTRICAS EM UM TRI NGULO QUALQUER As razões trigonométricas de ângulos obtusos Na semicircunferência do plano cartesiano, podemos provar uma propriedade importante para ângulos suplementares. Exemplo Se α + β = 180°, β = 180° − α, temos: sen α = sen(180° − α) cos α = − cos(180° − α) MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre

CAPÍTULO 10 – TRIGONOMETRIA DO TRI NGULO RET NGULO LEI DOS SENOS De modo geral, em qualquer triângulo vale: Teorema ou lei dos senos: Em todo triângulo, as medidas dos lados são proporcionais aos senos dos ângulos opostos, e a constante de proporcionalidade é a medida do diâmetro do círculo circunscrito a esse triângulo. Na figura, o ΔABC está inscrito no círculo de centro 0 e raio r. O teorema dos senos corresponde a: MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre

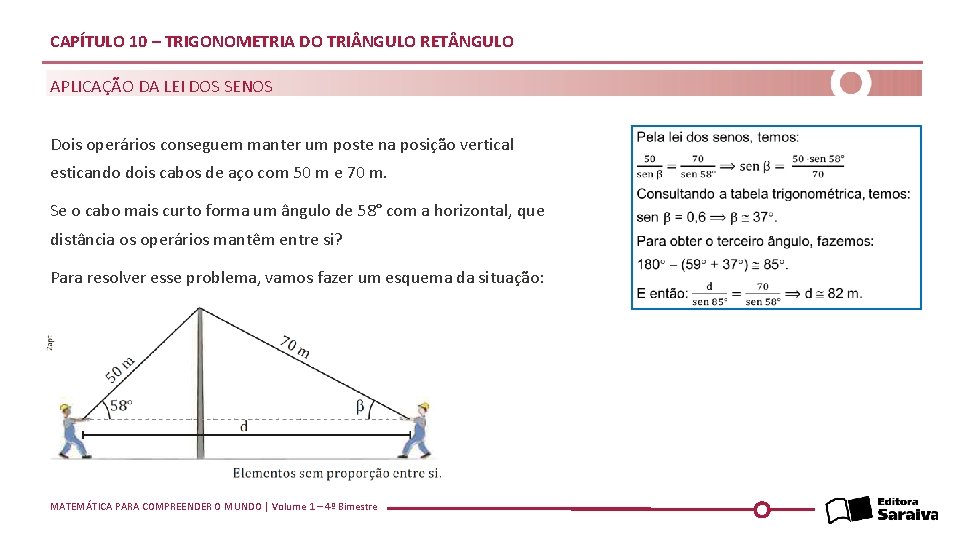
CAPÍTULO 10 – TRIGONOMETRIA DO TRI NGULO RET NGULO APLICAÇÃO DA LEI DOS SENOS Dois operários conseguem manter um poste na posição vertical esticando dois cabos de aço com 50 m e 70 m. Se o cabo mais curto forma um ângulo de 58° com a horizontal, que distância os operários mantêm entre si? Para resolver esse problema, vamos fazer um esquema da situação: MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre

CAPÍTULO 10 – TRIGONOMETRIA DO TRI NGULO RET NGULO LEI DOS SENOS Em geral, para se encontrar a medida de um dos lados de um triângulo, usando a lei dos senos, é necessário conhecer a medida de um dos outros lados e a de dois ângulos internos, ou a do ângulo oposto a esse lado e a medida do raio ou diâmetro da circunferência circunscrita a esse triângulo. Teorema da área A área S de um triângulo qualquer é igual ao semiproduto das medidas de dois lados pelo seno formado por esses lados. MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre

CAPÍTULO 10 – TRIGONOMETRIA DO TRI NGULO RET NGULO TEOREMA DOS COSSENOS OU LEI DOS COSSENOS Em todo triângulo, o quadrado da medida de um lado é igual à soma dos quadrados das medidas dos outros lados menos o duplo produto das medidas desses lados pelo cosseno do ângulo formado por eles. Em geral, para se encontrar a medida de um dos lados de um triângulo, usando a lei dos cossenos, é necessário conhecer a medida de um dos outros dois lados e a do ângulo interno oposto a esse lado. MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre

CAPÍTULO 10 – TRIGONOMETRIA DO TRI NGULO RET NGULO APLICAÇÃO DA LEI DOS COSSENOS Calcule a área do triângulo cujos lados medem 7 cm, 5 cm e 4 cm. Resolução: Pelo teorema ou lei dos cossenos, temos: MATEMÁTICA PARA COMPREENDER O MUNDO | Volume 1 – 4º Bimestre