Matematick programovn Ekonomick x matematick model lohy Formulace


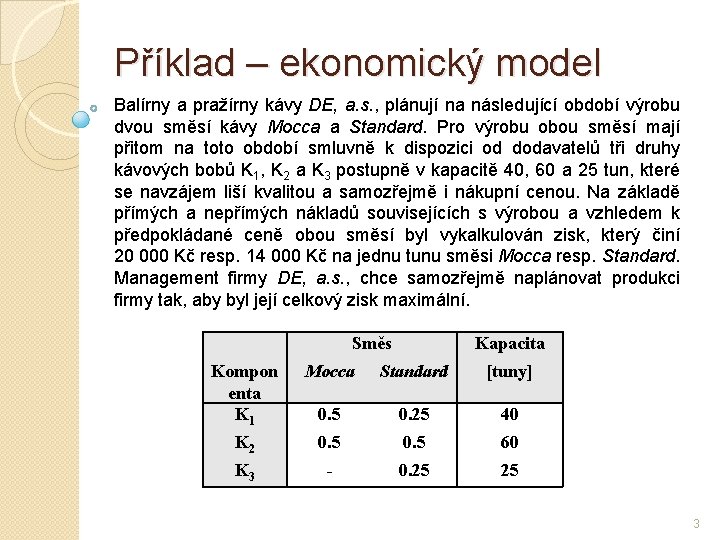

![Přípustné a nepřípustné programy směsi [tuny] program Moc Std 1 0 0 2 80 Přípustné a nepřípustné programy směsi [tuny] program Moc Std 1 0 0 2 80](https://slidetodoc.com/presentation_image_h2/464f84389da7ecc1270861843afdb82b/image-5.jpg)








- Slides: 19

Matematické programování Ekonomický x matematický model úlohy Formulace matematického modelu úlohy LP Grafické řešení úloh LP a základní pojmy Simplexová metoda Interpretace výsledků Formulace typických úloh LP 1

Úvod Matematický model úlohy MP: maximalizovat (minimalizovat) za podmínek 2

Příklad – ekonomický model Balírny a pražírny kávy DE, a. s. , plánují na následující období výrobu dvou směsí kávy Mocca a Standard. Pro výrobu obou směsí mají přitom na toto období smluvně k dispozici od dodavatelů tři druhy kávových bobů K 1, K 2 a K 3 postupně v kapacitě 40, 60 a 25 tun, které se navzájem liší kvalitou a samozřejmě i nákupní cenou. Na základě přímých a nepřímých nákladů souvisejících s výrobou a vzhledem k předpokládané ceně obou směsí byl vykalkulován zisk, který činí 20 000 Kč resp. 14 000 Kč na jednu tunu směsi Mocca resp. Standard. Management firmy DE, a. s. , chce samozřejmě naplánovat produkci firmy tak, aby byl její celkový zisk maximální. Směs Kapacita Kompon enta K 1 Mocca Standard [tuny] 0. 5 0. 25 40 K 2 0. 5 60 K 3 - 0. 25 25 3

Příklad – matematický model maximalizovat z = 20 000 x 1 + 14 000 x 2 , za podmínek 0. 5 x 1 + 0. 25 x 2 ≤ 40 , 0. 5 x 1 + 0. 5 x 2 ≤ 60 , 0. 25 x 2 ≤ 25 , x 1 ≥ 0, x 2 ≥ 0. (zisk) (K 1) (K 2) (K 3) • účelová (kriteriální) funkce (=zisk) • vlastní omezení úlohy (= K 1, K 2, K 3) • podmínky nezápornosti. 4
![Přípustné a nepřípustné programy směsi tuny program Moc Std 1 0 0 2 80 Přípustné a nepřípustné programy směsi [tuny] program Moc Std 1 0 0 2 80](https://slidetodoc.com/presentation_image_h2/464f84389da7ecc1270861843afdb82b/image-5.jpg)
Přípustné a nepřípustné programy směsi [tuny] program Moc Std 1 0 0 2 80 0 3 0 100 4 50 50 5 80 20 zbytek(+), nedostatek(-) kapacit K 1 K 2 K 3 40 60 25 0 20 25 15 10 0 25 10 12. 5 -5 10 20 zisk [tis. Kč] 0 1600 1400 1700 1880 5

Ekonomický model • cíl optimalizace (maximalizace zisku) • procesy, které probíhají v systému a jejich intenzita (výroba obou druhů směsí), činitelé, které ovlivňují provádění procesů (omezená zásoba surovin) • Matematický model účelová (kriteriální) funkce = lineární fce nproměnných • strukturní proměnné modelu (x 1, x 2, …, xn) • vlastní omezení ve formě lineárních rovnic/ nerovnic a podmínky nezápornosti. • 6

Obecný matematický model úlohy LP maximalizovat (minimalizovat) z = c 1 x 1 + c 2 x 2 +. . . + cnxn , za podmínek a 11 x 1 a 21 x 1 am 1 x 1 + a 12 x 2 +. . . + a 1 nxn ≤ b 1 , + a 22 x 2 +. . . + a 2 nxn ≤ b 2 , . : + am 2 x 2 +. . . + amnxn ≤ bm , xj ≥ 0 , j = 1, 2, . . . , n. n m cj , bi , počet strukturních proměnných modelu, počet vlastních omezení, j = 1, 2, . . . , n - cenový koeficient příslušející j-té proměnné, i = 1, 2, . . . , m - hodnota pravé strany příslušející i-tému omezení, 7

MM úlohy LP – sumace, matice maximalizovat (minimalizovat) za podmínek maximalizovat (minimalizovat) z = c. T x , za podmínek Ax ≤ b , x≥ 0, c. T = (c 1, c 2, . . . , cn) je n - složkový řádkový vektor cenových koeficientů, x = (x 1, x 2, . . . , xn)T je n-složkový sloupcový vektor strukturních proměnných modelu, b = (b 1, b 2, . . . , bm)T je m - složkový sloupcový vektor hodnot pravé strany, 0 = (0, 0, . . . , 0)T je n - složkový sloupcový nulový vektor a A je matice strukturních koeficientů o rozměru m x n. 8

Typické úlohy LP 1. Úlohy výrobního plánování (alokace zdrojů) 2. Úlohy finančního plánování (optimalizace portfolia) 3. Plánování reklamy (media selection problem) 4. Nutriční problém 5. Směšovací problém 6. Rozvrhování pracovníků 7. Úlohy o dělení materiálu 8. Distribuční úlohy LP 9

Základní pojmy LP Přípustné řešení úlohy LP je takové řešení, které vyhovuje všem podmínkám úlohy, tzn. všem vlastním omezením i podmínkám nezápornosti. Optimální řešení úlohy LP je přípustné řešení s nejlepší hodnotou účelové funkce (s nejvyšší hodnotou v případě maximalizace a nejnižší hodnotou v případě minimalizace účelové funkce). Základní (přípustné) řešení úlohy LP je takové přípustné řešení, které má maximálně tolik nenulových složek, kolik je lineárně nezávislých řádků ekvivalentní soustavy rovnic. Ekvivalentní soustava rovnic vznikne převedením původní soustavy nerovnic na rovnice pomocí doplňkových proměnných, které se označují jako přídatné proměnné (slack variables). 10

Ekvivalentní soustava rovnic Přídatné proměnné 0. 5 x 1 + 0. 25 x 2 ≤ 40 , 0. 5 x 1 + 0. 5 x 2 ≤ 60 , 0. 25 x 2 ≤ 25 , 0. 5 x 1 + 0. 25 x 2 + x 3 0. 5 x 1 + 0. 5 x 2 0. 25 x 2 typ omezení "≤" "≥" "=" (K 1) (K 2) (K 3) + x 4 + x 5 = 40 , = 60 , = 25. přídatná proměnná +x x 11

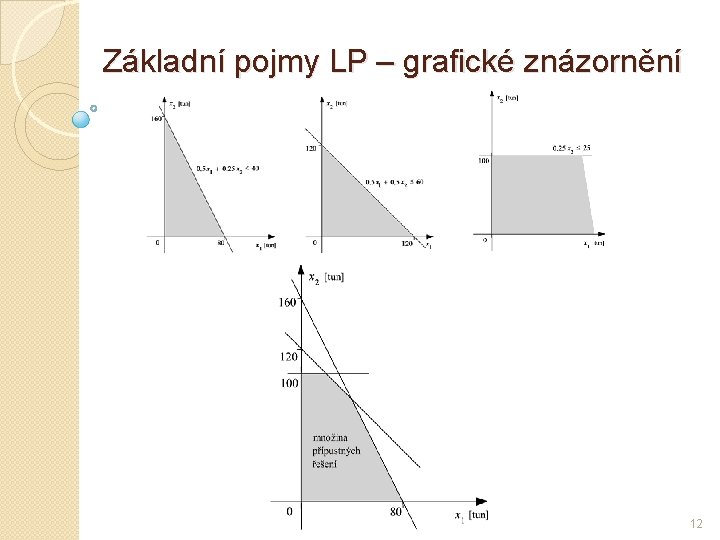
Základní pojmy LP – grafické znázornění 12

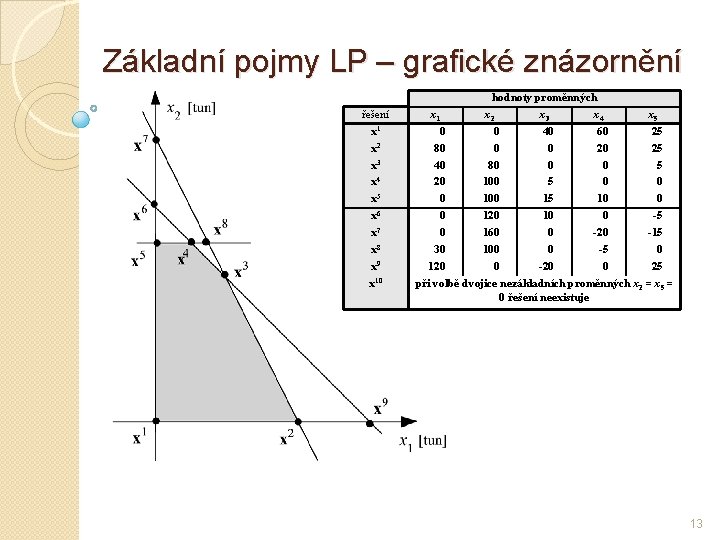
Základní pojmy LP – grafické znázornění řešení x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 hodnoty proměnných x 1 x 2 x 3 x 4 x 5 0 0 40 60 25 80 0 0 20 25 40 80 0 0 5 20 100 5 0 0 0 100 15 10 0 0 120 10 0 -5 0 160 0 -20 -15 30 100 0 -5 0 120 0 -20 0 25 při volbě dvojice nezákladních proměnných x 2 = x 5 = 0 řešení neexistuje 13

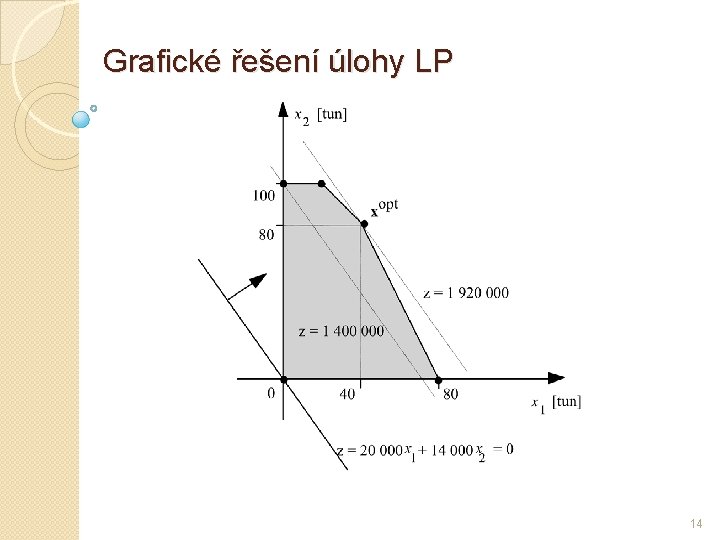
Grafické řešení úlohy LP 14

Základní věta LP a její význam Jestliže má úloha lineárního programování optimální řešení, potom má také optimální řešení základní. 1. Jestliže má úloha LP jediné optimální řešení, potom je to řešení základní. 2. Jestliže má úloha LP více optimálních řešení, potom alespoň jedno z nich je základní. Důsledek: Optimální řešení stačí hledat mezi řešeními základními, kterých je konečný počet. 15

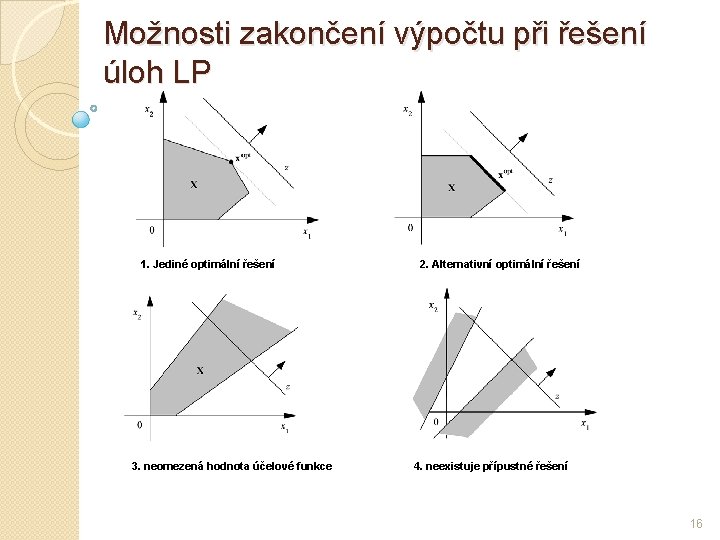
Možnosti zakončení výpočtu při řešení úloh LP 1. Jediné optimální řešení 3. neomezená hodnota účelové funkce 2. Alternativní optimální řešení 4. neexistuje přípustné řešení 16

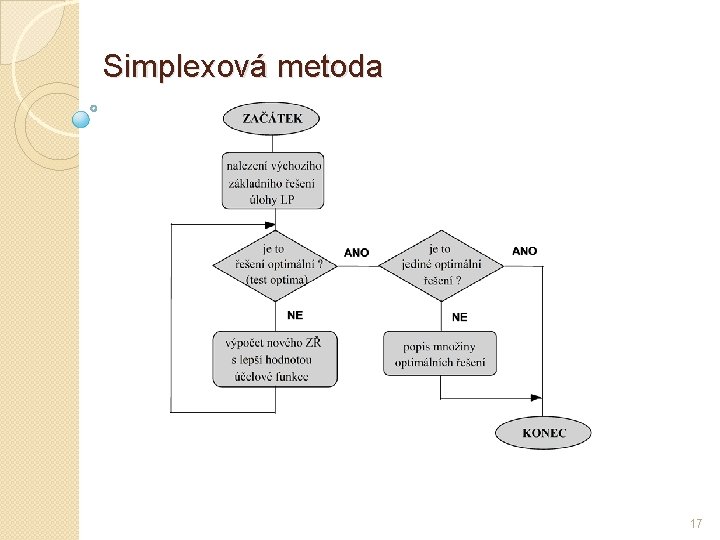
Simplexová metoda 17

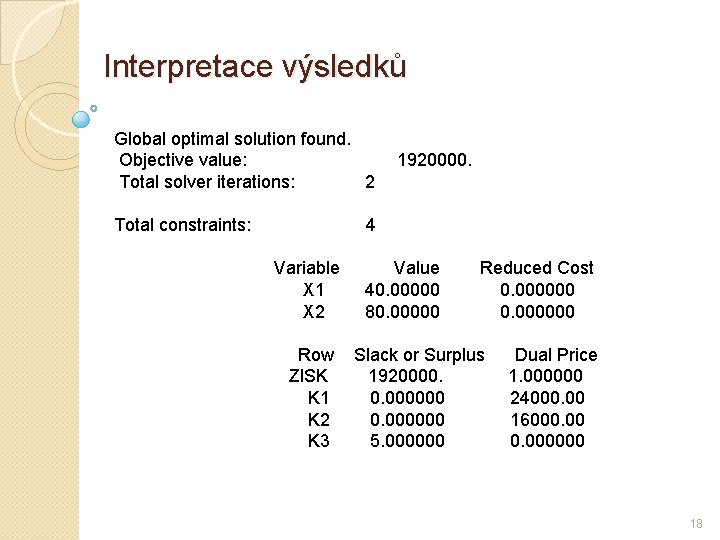
Interpretace výsledků Global optimal solution found. Objective value: Total solver iterations: 2 Total constraints: 1920000. 4 Variable X 1 X 2 Row ZISK K 1 K 2 K 3 Value 40. 00000 80. 00000 Reduced Cost 0. 000000 Slack or Surplus 1920000. 0. 000000 5. 000000 Dual Price 1. 000000 24000. 00 16000. 000000 18

Interpretace výsledků Hodnoty strukturních proměnných (Value) Udávají úroveň jednotlivých procesů modelu (objem výroby obou druhů směsí) Hodnoty přídatných proměnných (Slack or Surplus) Udávají rozdíl mezi pravou a levou stranou (případně mezi levou a pravou stranou) omezujících podmínek (nevyužitá kapacita surovin) Stínové ceny (shadow/dual price) Lze interpretovat jako ocenění jedné jednotky pravé strany ve vztahu k hodnotě účelové funkce. Jedná se tedy vlastně o marginální ocenění pravých stran (podíl jedné tuny kapacity suroviny K na celkovém zisku) Redukované ceny (reduced cost) Udávají, o kolik je třeba zvýšit přínos daného procesu, aby byl efektivní (aby se daný výrobek vyráběl) 19