Margins on Nyquist plot Suppose Draw Nyquist plot





























- Slides: 38

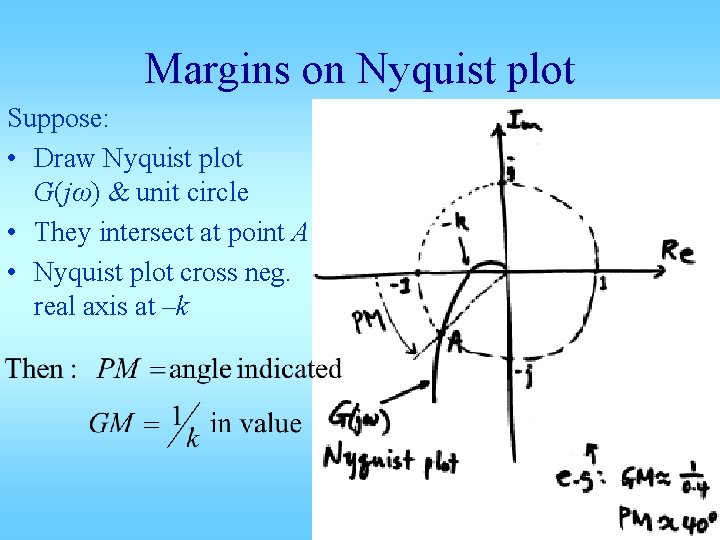
Margins on Nyquist plot Suppose: • Draw Nyquist plot G(jω) & unit circle • They intersect at point A • Nyquist plot cross neg. real axis at –k

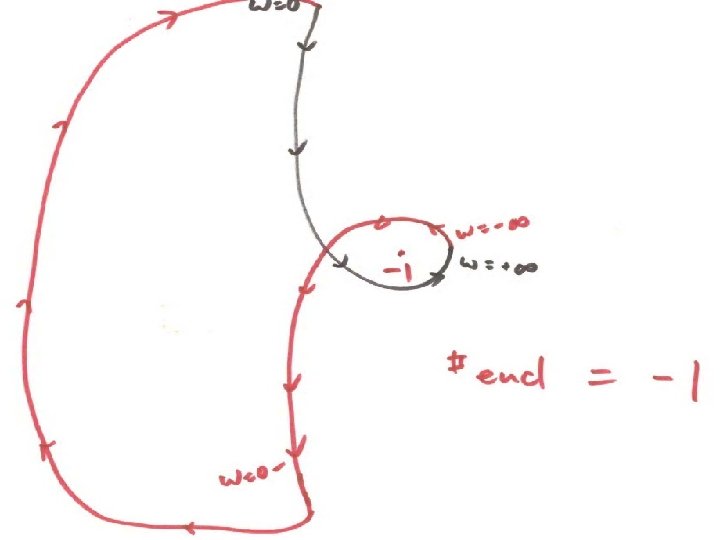
Stability from Nyquist plot The complete Nyquist plot: – Plot G(jω) for ω = 0+ to +∞ – Get complex conjugate of plot, that’s G(jω) for ω = 0– to –∞ – If G(s) has pole on jω-axis, treat separately – Mark direction of ω increasing – Locate point: – 1


Encirclement of the -1 point • As you follow along the G(jω) curve for one complete cycle, you may “encircle” the – 1 point • Going around in c. w. once is +1 encirclement • c. c. w. once is – 1 encirclement




Nyquist Criterion Theorem # (unstable poles of closed-loop) Z = # (unstable poles of open-loop) + # encirclement or: Z = P + N To have closed-loop stable: need Z = 0, i. e. N = –P P N

That is: G(jω) needs to encircle the “– 1” point c. c. w. P times. If open loop is stable to begin with, G(jω) cannot encircle the “– 1” point for closed -loop stability In previous example: 1. No encirclement, N = 0. 2. Open-loop stable, P = 0 3. Z = P + N = 0, no unstable poles in closed-loop, stable

Example:

As you move around from ω = –∞ to 0–, to 0+, to +∞, you go around “– 1” c. c. w. once. # encirclement N = – 1. # unstable pole P = 1

i. e. # unstable poles of closed-loop = 0 closed-loop system is stable. Check: c. l. pole at s = – 3, stable.

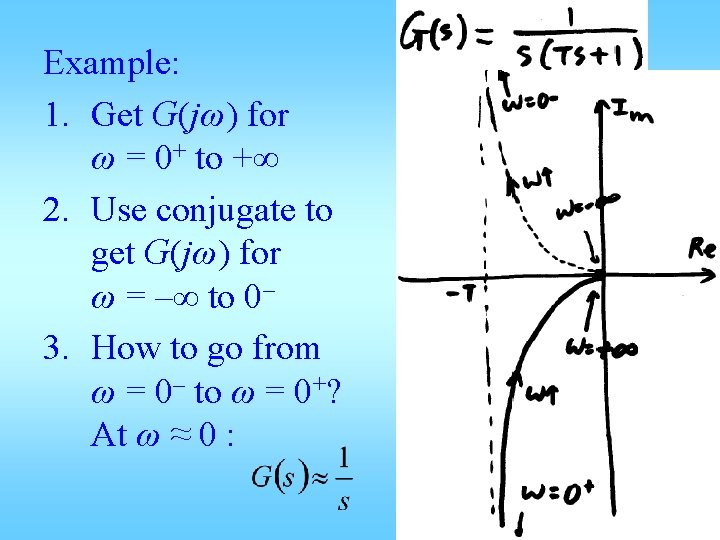
Example: 1. Get G(jω) for ω = 0+ to +∞ 2. Use conjugate to get G(jω) for ω = –∞ to 0– 3. How to go from ω = 0– to ω = 0+? At ω ≈ 0 :



# encirclement N = _____ # open-loop unstable poles P = _____ Z = P + N = ____ = # closed-loop unstable poles. closed-loop stability: _______

Example: Given: 1. G(s) is stable 2. With K = 1, performed open-loop sinusoidal tests, and G(jω) is on next page Q: 1. Find stability margins 2. Find Nyquist criterion to determine closed-loop stability


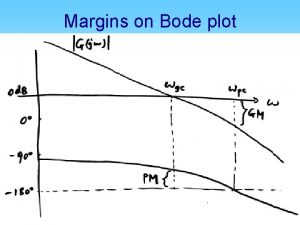
Solution: 1. Where does G(jω) cross the unit circle? ____ Phase margin ≈ ____ Where does G(jω) cross the negative real axis? ____ Gain margin ≈ ____ Is closed-loop system stable with K = 1? ____

Note that the total loop T. F. is KG(s). If K is not = 1, Nyquist plot of KG(s) is a scaling of G(jω). e. g. If K = 2, scale G(jω) by a factor of 2 in all directions. Q: How much can K increase before GM becomes lost? ____ How much can K decrease? ______

Some people say the gain margin is 0 to 5 in this example Q: As K is increased from 1 to 5, GM is lost, what happens to PM? What’s the max PM as K is reduced to 0 and GM becomes ∞?

2. To use Nyquist criterion, need complete Nyquist plot. a) Get complex conjugate b) Connect ω = 0– to ω = 0+ through an infinite circle c) Count # encirclement N d) Apply: Z = P + N o. l. stable, P = _______ Z = _______ c. l. stability: _______


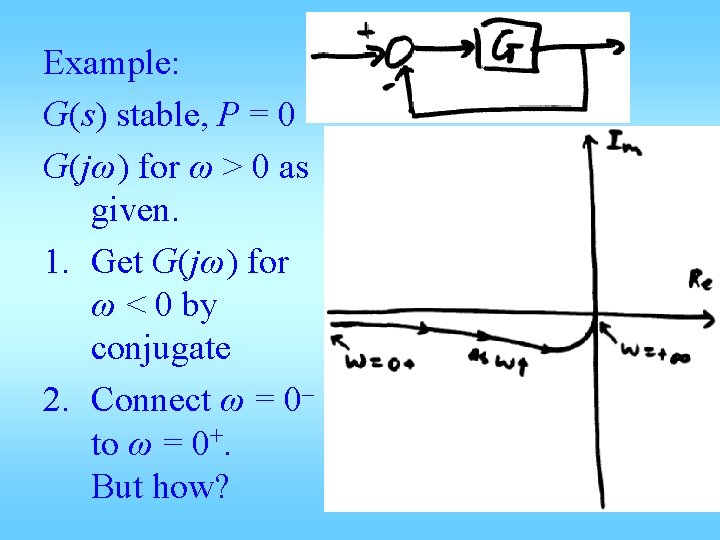
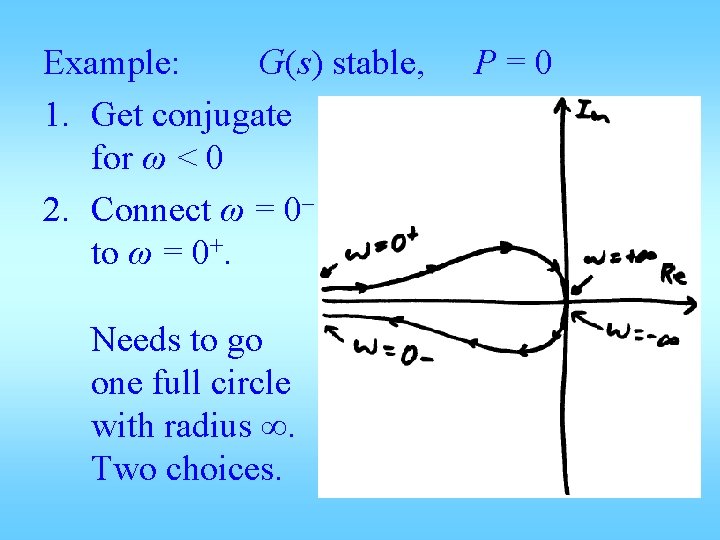
Example: G(s) stable, P = 0 G(jω) for ω > 0 as given. 1. Get G(jω) for ω < 0 by conjugate 2. Connect ω = 0– to ω = 0+. But how?

Choice a) : Where’s “– 1” ? # encirclement N = _______ Z = P + N = _______ Make sense? _______

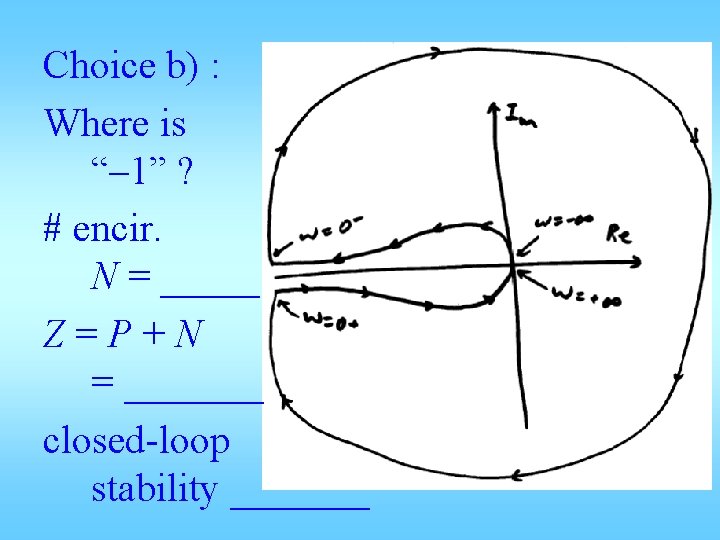
Choice b) : Where is “– 1” ? # encir. N = _____ Z=P+N = _______ closed-loop stability _______

Note: If G(jω) is along –Re axis to ∞ as ω→ 0+, it means G(s) has in it. when s makes a half circle near ω = 0, G(s) makes a full circle near ∞. choice a) is impossible, but choice b) is possible.


Example: G(s) stable, 1. Get conjugate for ω < 0 2. Connect ω = 0– to ω = 0+. Needs to go one full circle with radius ∞. Two choices. P=0

Choice a) : N=0 Z=P+N=0 closed-loop stable

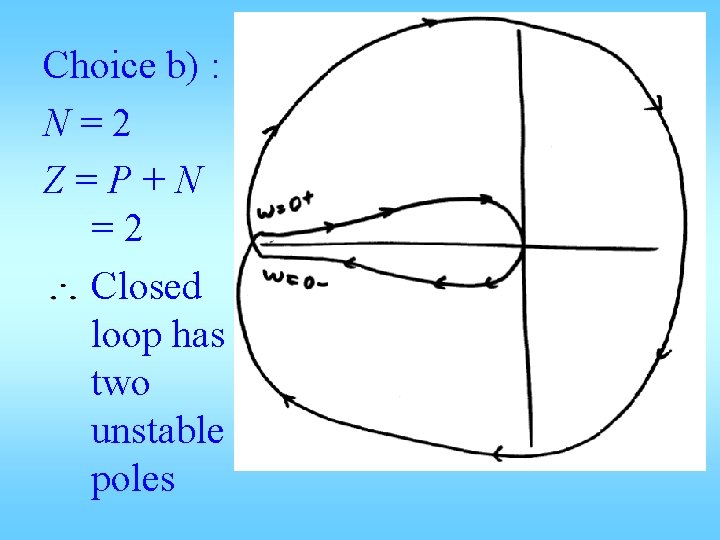
Choice b) : N=2 Z=P+N =2 Closed loop has two unstable poles

Which way is correct? For stable & non-minimum phase systems,

Example: G(s) has one unstable pole P = 1, no unstable zeros 1. Get conjugate 2. Connect ω = 0– to ω = 0+. How? One unstable pole/zero If connect in c. c. w.

# encirclement N = ? If “– 1” is to the left of A i. e. A > – 1 then N = 0 Z=P+N=1+0=1 but if a gain is increased, “– 1” could be inside, N = – 2 Z = P + N = – 1 c. c. w. is impossible

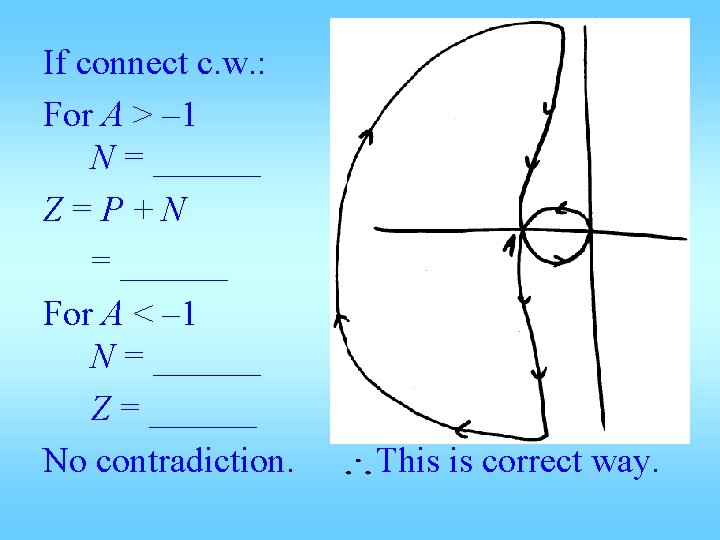
If connect c. w. : For A > – 1 N = ______ Z=P+N = ______ For A < – 1 N = ______ Z = ______ No contradiction. This is correct way.

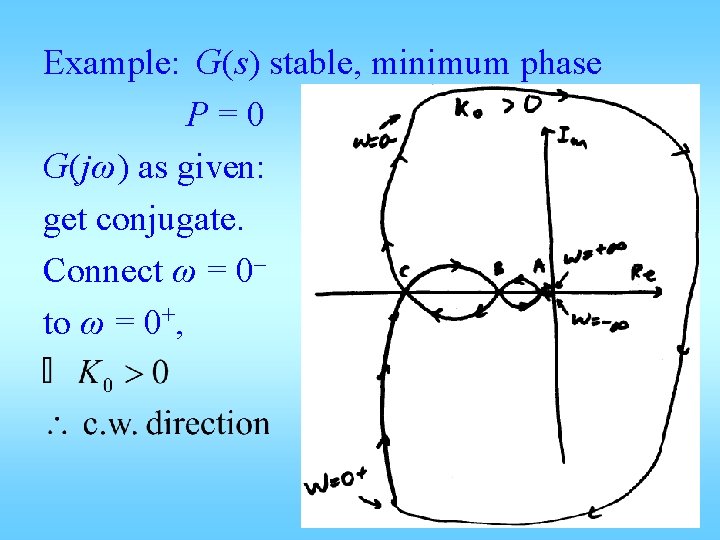
Example: G(s) stable, minimum phase P=0 G(jω) as given: get conjugate. Connect ω = 0– to ω = 0+,

If A < – 1 < 0 : N = ______ Z = P + N = ______ stability of c. l. : ______ If B < – 1 < A : N = ______ Z = P + N = ______ closed-loop stability: ______

If C < – 1 < B : N = ______ Z = P + N = ______ closed-loop stability: ______ If – 1 < C : N = ______ Z = P + N = ______ closed-loop stability: ______
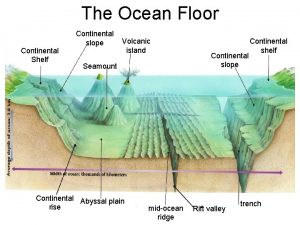
 How to sketch a nyquist plot
How to sketch a nyquist plot Ocean basin
Ocean basin Margins, dydx stata
Margins, dydx stata What type of forces dominate at convergent plate margins
What type of forces dominate at convergent plate margins Subject contrast
Subject contrast Filamentous bacteria colony
Filamentous bacteria colony Is apa in times new roman
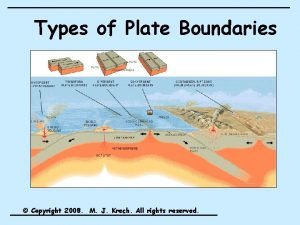
Is apa in times new roman Type of plate boundary
Type of plate boundary Incised leaf
Incised leaf Nsf margins
Nsf margins Margins
Margins Shelf break
Shelf break Prevmar
Prevmar Freshman google doc
Freshman google doc Bode diyagramı çizimi
Bode diyagramı çizimi First order lag filter
First order lag filter State and explain nyquist stability criterion.
State and explain nyquist stability criterion. Nyquist plot
Nyquist plot How to draw use case diagram in draw.io
How to draw use case diagram in draw.io Draw near unto me and i will draw unto you
Draw near unto me and i will draw unto you How to draw a box plot from a cumulative frequency graph
How to draw a box plot from a cumulative frequency graph Cumulative frequency box plots
Cumulative frequency box plots Bande de nyquist
Bande de nyquist Nyquist stability criterion
Nyquist stability criterion Wolfram nyquist
Wolfram nyquist Anders nyquist
Anders nyquist Ali nyquist
Ali nyquist Teorema de nyquist amostragem
Teorema de nyquist amostragem Bande de nyquist
Bande de nyquist Aliasing
Aliasing Nyquist diyagramı
Nyquist diyagramı Bande de nyquist
Bande de nyquist Nyquist aliasing
Nyquist aliasing Nyquist criterion for distortionless transmission
Nyquist criterion for distortionless transmission L suppose
L suppose Suppose your car was mired deeply in the mud
Suppose your car was mired deeply in the mud Cocomo kloc
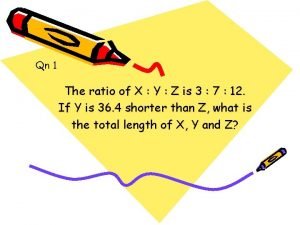
Cocomo kloc Qn-1
Qn-1 The cask of amontillado reading
The cask of amontillado reading