Mesures dans le domaine frquentiel Plan Notions lmentaires

Mesures dans le domaine fréquentiel

Plan • • • Notions élémentaires sur les mesures dans le domaine fréquentiel Considérations sur le domaine temporel Analyses en fréquence

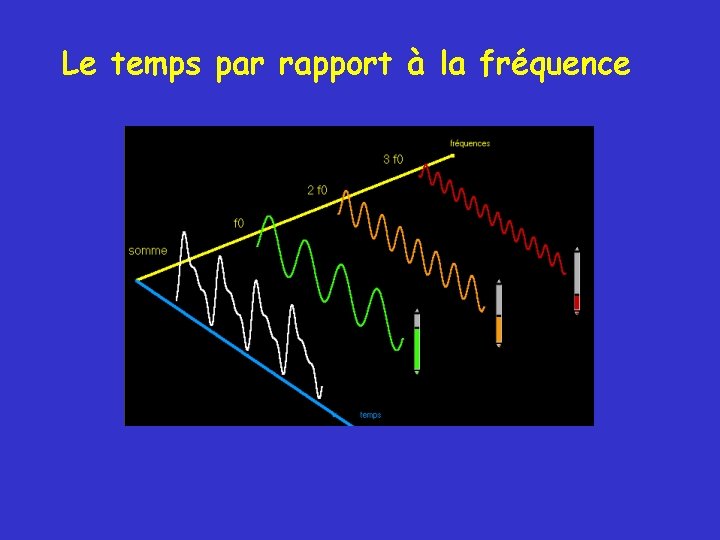
Le temps par rapport à la fréquence

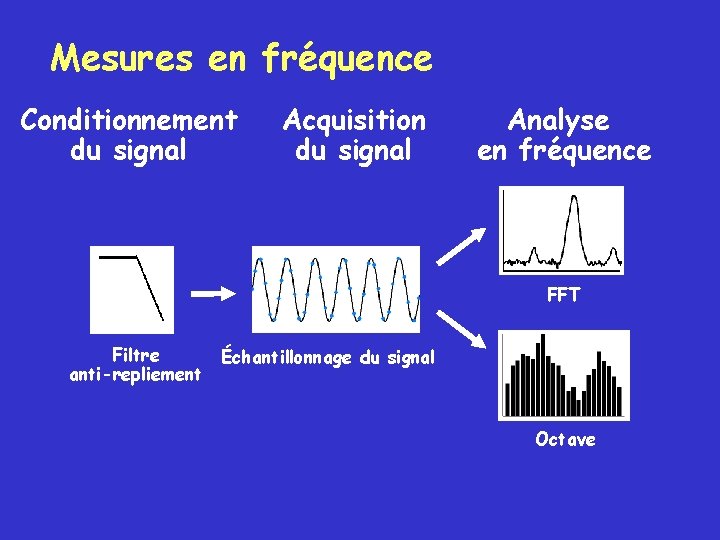
Mesures en fréquence Conditionnement du signal Acquisition du signal Analyse en fréquence FFT Filtre anti-repliement Échantillonnage du signal Octave

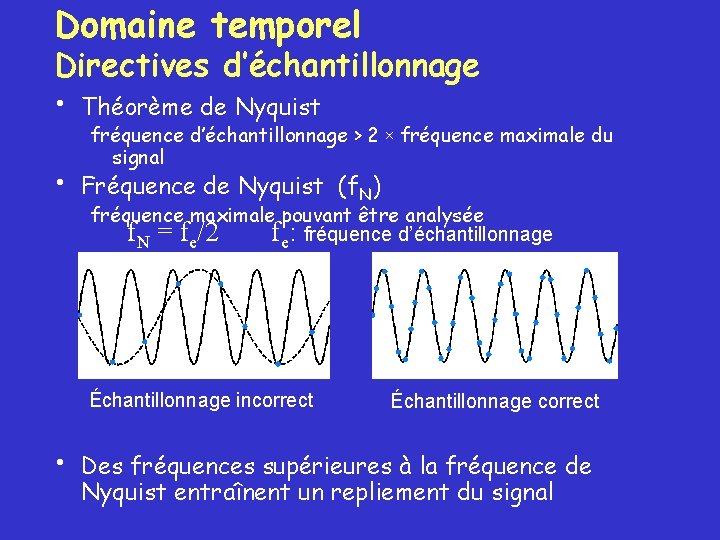
Domaine temporel Directives d’échantillonnage • Théorème de Nyquist • fréquence d’échantillonnage > 2 signal fréquence maximale du Fréquence de Nyquist (f. N) fréquence maximale pouvant être analysée f. N = fe/2 fe: fréquence d’échantillonnage Échantillonnage incorrect • x Échantillonnage correct Des fréquences supérieures à la fréquence de Nyquist entraînent un repliement du signal

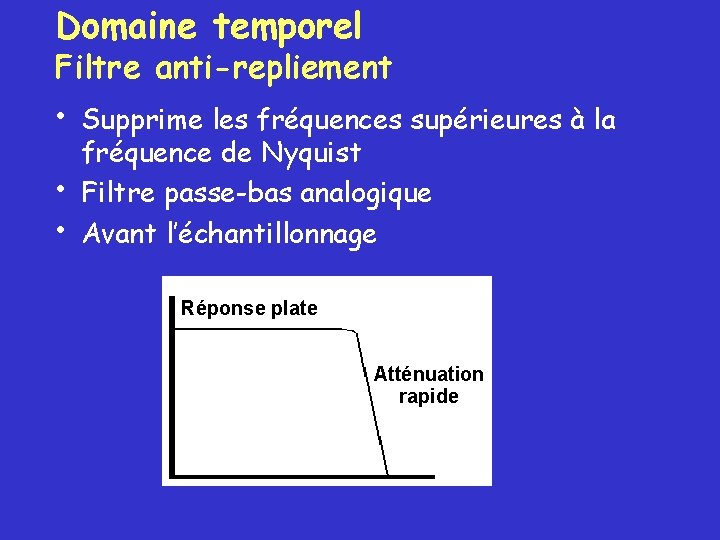
Domaine temporel Filtre anti-repliement • • • Supprime les fréquences supérieures à la fréquence de Nyquist Filtre passe-bas analogique Avant l’échantillonnage Réponse plate Atténuation rapide

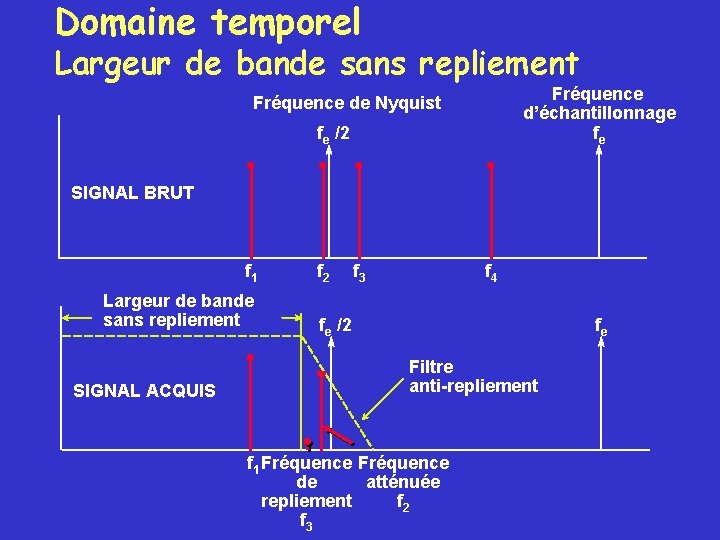
Domaine temporel Largeur de bande sans repliement Fréquence d’échantillonnage fe Fréquence de Nyquist fe /2 SIGNAL BRUT f 1 Largeur de bande sans repliement SIGNAL ACQUIS f 2 f 3 f 4 fe /2 fe Filtre anti-repliement f 1 Fréquence de atténuée repliement f 2 f 3

Domaine temporel • Éléments supplémentaires Convertisseur analogique/numérique D/S – Haute résolution – Filtres anti-repliement intégrés – Adapté pour la mesure de sons et de vibrations • Échantillonnage et déclenchement simultanés • Gain programmable • Détection de surtension – Relation entre les phases des signaux

Analyse du domaine fréquentiel • Analyse par FFT • Analyse par octave • Analyse par wobulation

FFT • La FFT donne des informations sur l’amplitude et la phase • Le spectre de puissance représente l’énergie contenue dans le signal • – Amplitude = (Réelle^2 + Imag^2) – Phase = Arc tan (Imag / Réelle) – Spectre de puissance = Amplitude ^2 Applications • • Analyse de vibrations Test dynamique de structure Maintenance préventive Test de chocs

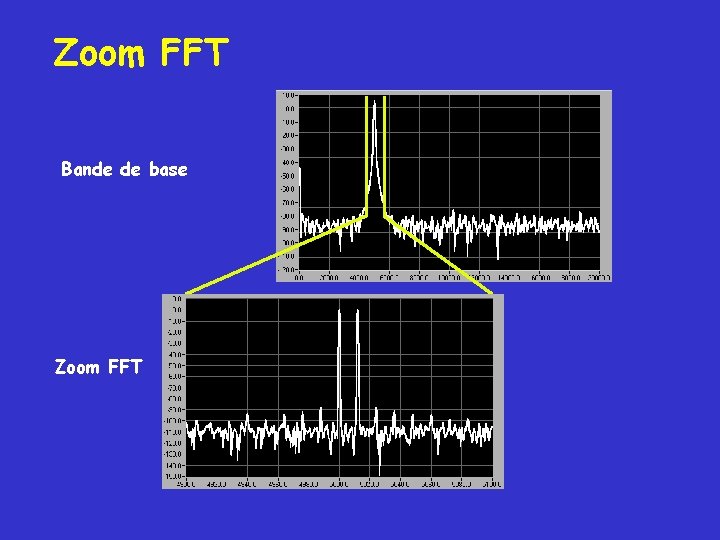
Zoom FFT Bande de base Zoom FFT

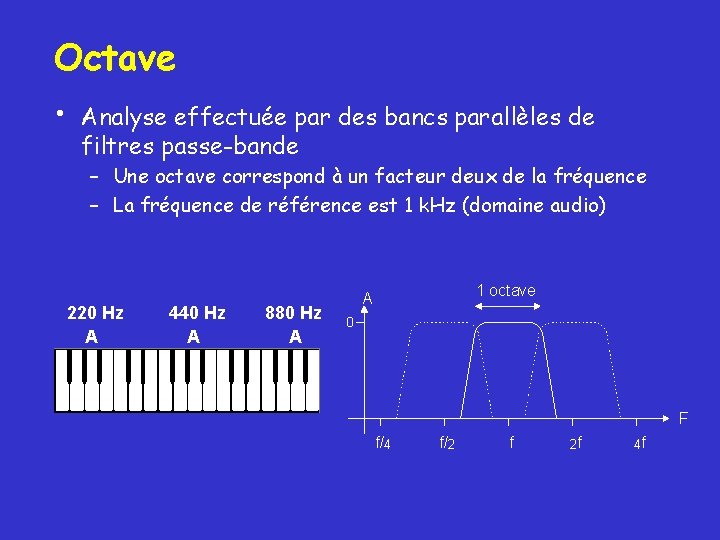
Octave • Analyse effectuée par des bancs parallèles de filtres passe-bande – Une octave correspond à un facteur deux de la fréquence – La fréquence de référence est 1 k. Hz (domaine audio) 220 Hz A 440 Hz A 880 Hz A 1 octave A 0 F f/4 f/2 f 2 f 4 f

Octave • Octave : échelle des fréquences logarithmique • • – Similaire à la perception des sons par l’oreille humaine – Analyses en 1/1, 1/3, 1/12, et 1/24 d’octave FFT : échelle des fréquences linéaire Applications – – Test des émissions de bruit Mesure d’intensité acoustique Mesure de puissance sonore Equalizer

Wobulation Périphériqu en cours ede test Source • • • Réponse en fréquence Générations successives couvrant une gamme de fréquences. À chaque étape, l’analyseur mesure l’amplitude et la phase pour chaque fréquence. de FFT

Wobulation • Auto-résolution • Applications – Wobulation optimisée : plus de temps à basses fréquences et moins à hautes fréquences – Augmente la résolution en fréquence pour de grandes variations de la réponse – Test de haut-parleur – Test de téléphone cellulaire – Caractérisation d’équipement électronique

Comparaison des méthodes d’analyse fréquentielle • FFT • Octave • Wobulation – Très rapide – Échelle des fréquences linéaire – Fondée sur la TFD – Échelle des fréquences logarithmique – Banc de filtres divisant le spectre en bandes – Similitude avec l’oreille humaine dans le domaine fréquentiel – Bonne gamme de données dynamique – Source et analyseur pour chaque étape de fréquence – Réponse lente