LMITES Y CONTINUIDAD DE FUNCIONES U D 7

LÍMITES Y CONTINUIDAD DE FUNCIONES U. D. 7 * 1º BCT @ Angel Prieto Benito Apuntes 1º Bachillerato CT 1

LÍMITE DE UNA FUNCIÓN EN UN PUNTO U. D. 7. 4 * 1º BCT @ Angel Prieto Benito Apuntes 1º Bachillerato CT 2

LÍMITE DE UNA FUNCIÓN EN UN PUNTO • LIMITE de una función f en un punto x = a , cuando x tiende a a es el valor al que se aproximan las imágenes de la función cuando x se aproxima al valor a, tanto por su derecha como por su izquierda. lím f(x) = b x a Nota: Aunque pueden coincidir, en general los números lim f(x) y f(a) no están relacionados entre sí. x a • • • EJEMPLO: lím x 2 = 22 = 4 x 2 Sucesión de x : 1’ 9, 1’ 999, … Sucesión de las correspondientes imágenes: 3’ 96, 3’ 98, 3’ 99, … @ Angel Prieto Benito Apuntes 1º Bachillerato CT 3

LÍMITES LATERALES EN UN PUNTO • • • En un límite vemos que x puede tender al valor de “a” tomando valores tanto por su derecha como por su izquierda. Por ejemplo, puede tender a 2 tomando las siguientes sucesiones de números: 2’ 1, 2’ 001, 2’ 00001, … 1’ 9, 1’ 999, 1’ 99999, … Se hace preciso distinguir ambos límites. LIMITE POR LA DERECHA lím f(x) = L 1 x a+ LIMITE POR LA IZQUIERDA lím f(x) = L 2 x a -Una función f tiene límite en un punto a si sus límites laterales en dicho punto existen y coinciden. Entonces L 1 = L 2 = b @ Angel Prieto Benito Apuntes 1º Bachillerato CT 4

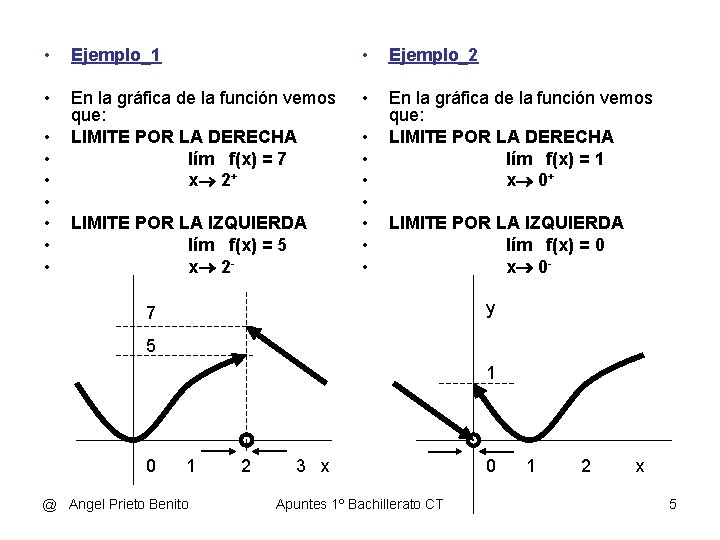
• Ejemplo_1 • Ejemplo_2 • En la gráfica de la función vemos que: LIMITE POR LA DERECHA lím f(x) = 7 x 2+ • En la gráfica de la función vemos que: LIMITE POR LA DERECHA lím f(x) = 1 x 0+ • • LIMITE POR LA IZQUIERDA lím f(x) = 5 x 2 - • • LIMITE POR LA IZQUIERDA lím f(x) = 0 x 0 y 7 5 1 0 1 @ Angel Prieto Benito 2 3 x Apuntes 1º Bachillerato CT 0 1 2 x 5

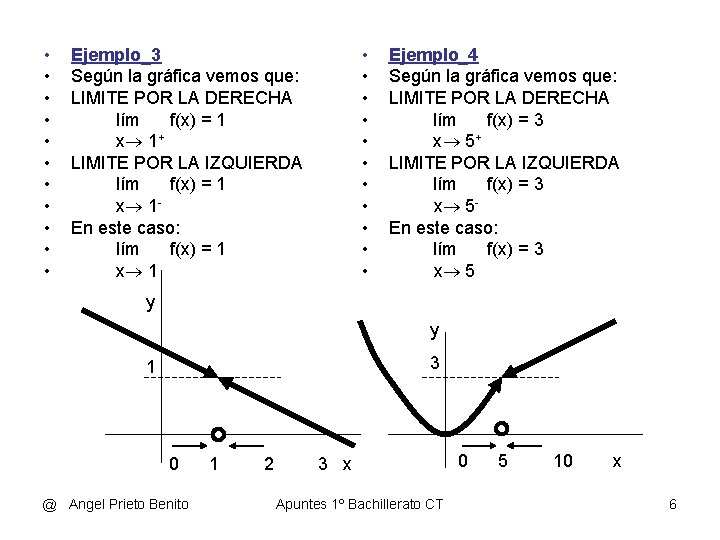
• • • • • • Ejemplo_3 Según la gráfica vemos que: LIMITE POR LA DERECHA lím f(x) = 1 x 1+ LIMITE POR LA IZQUIERDA lím f(x) = 1 x 1 En este caso: lím f(x) = 1 x 1 Ejemplo_4 Según la gráfica vemos que: LIMITE POR LA DERECHA lím f(x) = 3 x 5+ LIMITE POR LA IZQUIERDA lím f(x) = 3 x 5 En este caso: lím f(x) = 3 x 5 y y 3 1 0 @ Angel Prieto Benito 1 2 3 x Apuntes 1º Bachillerato CT 0 5 10 x 6

• • • • Ejemplo_5 x– 4 Lím ------x 1 x – 2 • • • • x y ------------0, 99 2, 9802 0, 999 2, 9980 1 ? 1, 001 3, 0020 1, 01 3, 0202 1, 1 3, 2020 • Como se puede intuir, el límite de la función cuando x 1 es 3 @ Angel Prieto Benito Ejemplo_6 x– 3 Lím -----x 3 x 2 – 9 x y ------------2, 99 0, 1669 2, 999 0, 1667 2, 9999 0, 1666 3 ? 3, 0001 0, 1666 3, 001 0, 1667 • Como se puede intuir, el límite de la función cuando x 3 es 1/6 Apuntes 1º Bachillerato CT 7

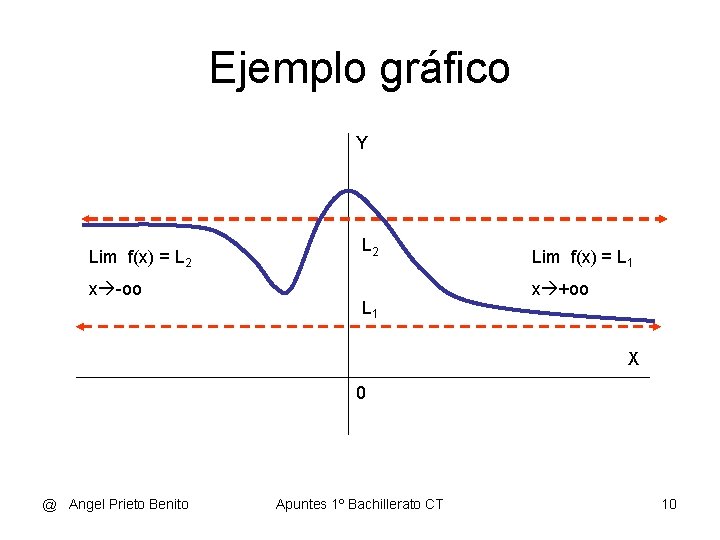
LIMITES EN EL INFINITO • • • El límite de una función f, cuando x tiende a ± oo, es L si para cualquier sucesión de valores de x que tienda a oo, el límite de la sucesión de las correspondientes imágenes es L. lím f(x) = L 1 lím f(x) = L 2 x +oo x –oo En caso de existir límite en el infinito decimos que f presenta una asíntota horizontal. (O dos, si L 1 es distinto de L 2 ) • Ejemplo • f(x) = x / (x – 3) • • Para x = 1000 y = 1000/997 = 1, 003 Para x=10000 y = 10000/9997 = 1, 0003 Para x = 100000 y = 1, 00003 Está claro que por mucho que aumente la variable x, el valor de y cambia muy poco y además se acerca a y=1, aunque nunca llega. @ Angel Prieto Benito Apuntes 1º Bachillerato CT 8

• Otro ejemplo • y = x / (x 2 – 4) • • Para x = 1000 y = 1000/999996 = 0, 001 Para x=10000 y = 10000/9999996 = 0, 0001 Para x = 100000 y = 0, 00001 Para x = 1000000 y = 0, 000001 • • • Está ya claro que: Lím f(x) = 0 x +oo • Si x toma valores negativos muy grandes, el valor de f(x) seguirá una sucesión de valores idéntica, aunque ahora negativos. Lím f(x) = 0 x – oo • • La función presenta una recta asíntota horizontal que es y = 0. Si los dos límites hallados fueran de distinto valor, la función tendría dos asíntotas horizontales: y = L 1 e y = L 2 @ Angel Prieto Benito Apuntes 1º Bachillerato CT 9

Ejemplo gráfico Y Lim f(x) = L 2 x -oo L 2 L 1 Lim f(x) = L 1 x +oo X 0 @ Angel Prieto Benito Apuntes 1º Bachillerato CT 10

LIMITES INFINITOS • • • • Si a es un número real, lím f(x) = +oo significa que cuando x tome valores x a muy próximos a a, a ambos lados, los correspondientes valores de f se harán arbitrariamente grandes. De forma análoga se define lím f(x) = –oo. x a Si a es un número real, lím f(x) = +oo significa que cuando x tome valores x a+ muy próximos a a, pero mayores que a, los correspondientes valores de f se harán arbitrariamente grandes. De forma análoga se define lím f(x) = –oo. x a+ Y también lím f(x) = +oo o lím f(x) = –oo. x ax a- @ Angel Prieto Benito Apuntes 1º Bachillerato CT 11

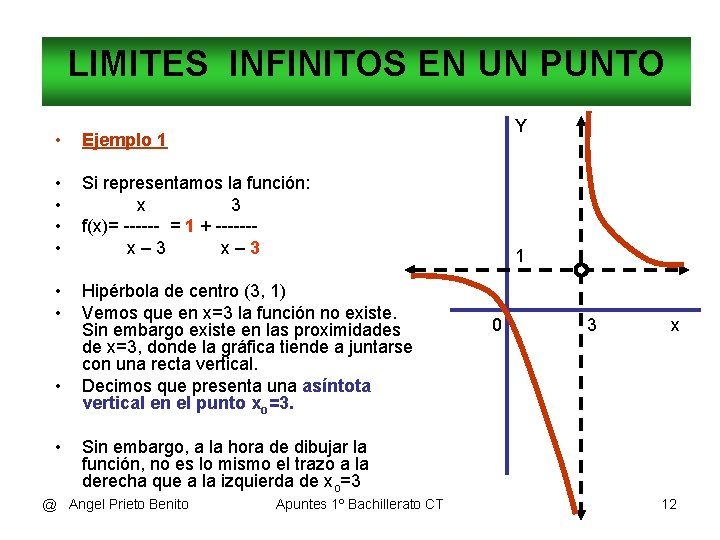
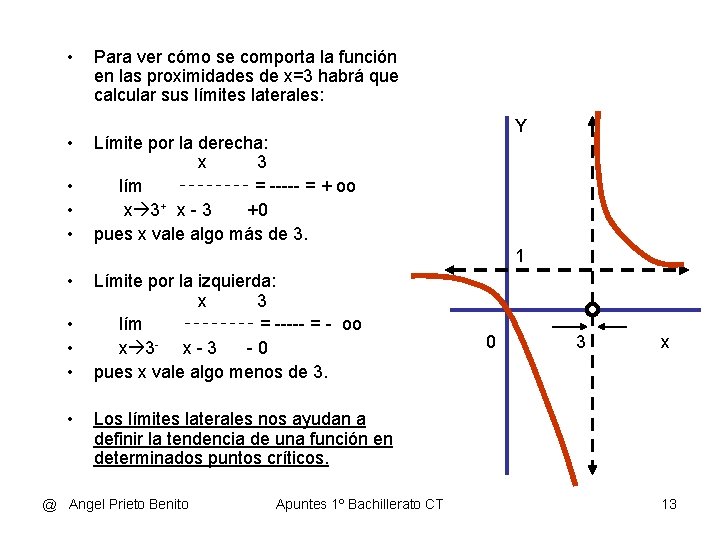
LIMITES INFINITOS EN UN PUNTO Y • Ejemplo 1 • • Si representamos la función: x 3 f(x)= ------ = 1 + ------x– 3 • • Hipérbola de centro (3, 1) Vemos que en x=3 la función no existe. Sin embargo existe en las proximidades de x=3, donde la gráfica tiende a juntarse con una recta vertical. Decimos que presenta una asíntota vertical en el punto xo=3. • • 1 0 3 x Sin embargo, a la hora de dibujar la función, no es lo mismo el trazo a la derecha que a la izquierda de xo=3 @ Angel Prieto Benito Apuntes 1º Bachillerato CT 12

• • • Para ver cómo se comporta la función en las proximidades de x=3 habrá que calcular sus límites laterales: Y Límite por la derecha: x 3 lím ‑‑‑‑ = ----- = + oo x 3+ x - 3 +0 pues x vale algo más de 3. 1 • • • Límite por la izquierda: x 3 lím ‑‑‑‑ = ----- = - oo x 3 - x - 3 -0 pues x vale algo menos de 3. 0 3 x Los límites laterales nos ayudan a definir la tendencia de una función en determinados puntos críticos. @ Angel Prieto Benito Apuntes 1º Bachillerato CT 13

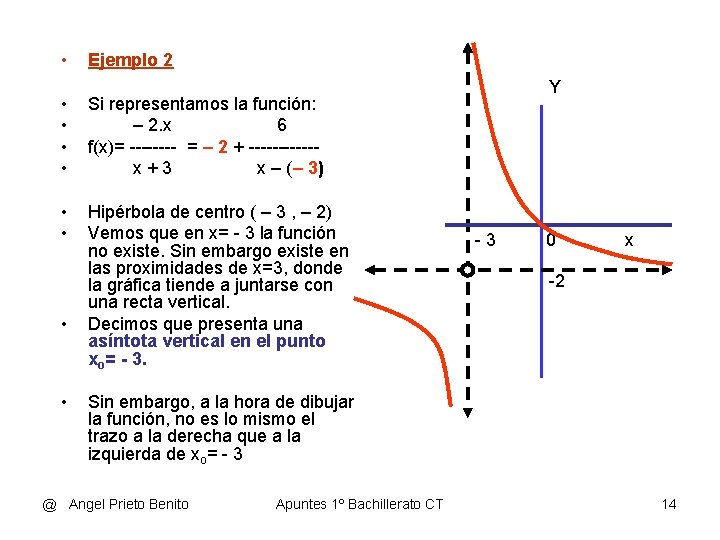
• Ejemplo 2 • • Si representamos la función: – 2. x 6 f(x)= ---- = – 2 + ------x+3 x – (– 3) • • Hipérbola de centro ( – 3 , – 2) Vemos que en x= - 3 la función no existe. Sin embargo existe en las proximidades de x=3, donde la gráfica tiende a juntarse con una recta vertical. Decimos que presenta una asíntota vertical en el punto xo= - 3. • • Y -3 0 x -2 Sin embargo, a la hora de dibujar la función, no es lo mismo el trazo a la derecha que a la izquierda de xo= - 3 @ Angel Prieto Benito Apuntes 1º Bachillerato CT 14

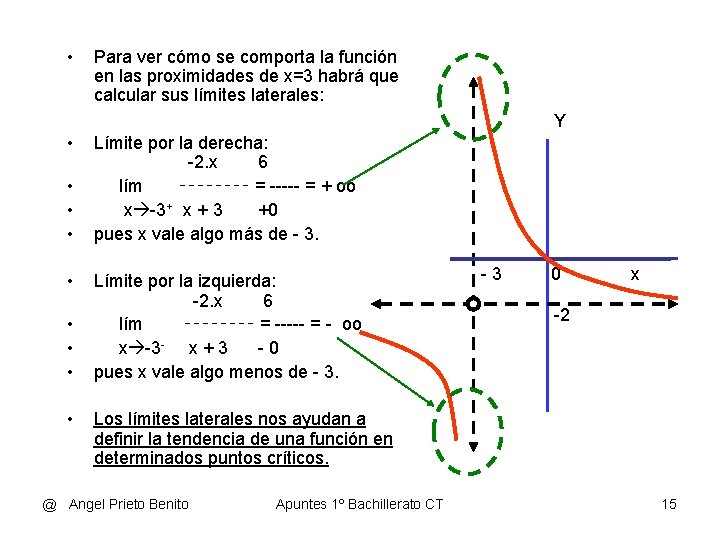
• Para ver cómo se comporta la función en las proximidades de x=3 habrá que calcular sus límites laterales: Y • • • Límite por la derecha: -2. x 6 lím ‑‑‑‑ = ----- = + oo x -3+ x + 3 +0 pues x vale algo más de - 3. Límite por la izquierda: -2. x 6 lím ‑‑‑‑ = ----- = - oo x -3 - x + 3 -0 pues x vale algo menos de - 3. -3 0 x -2 Los límites laterales nos ayudan a definir la tendencia de una función en determinados puntos críticos. @ Angel Prieto Benito Apuntes 1º Bachillerato CT 15

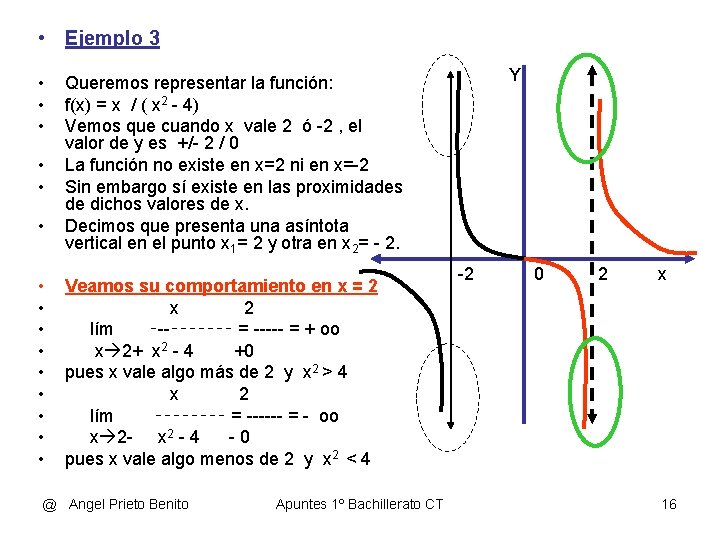
• Ejemplo 3 • • • • Y Queremos representar la función: f(x) = x / ( x 2 - 4) Vemos que cuando x vale 2 ó -2 , el valor de y es +/- 2 / 0 La función no existe en x=2 ni en x=-2 Sin embargo sí existe en las proximidades de dichos valores de x. Decimos que presenta una asíntota vertical en el punto x 1= 2 y otra en x 2= - 2. Veamos su comportamiento en x = 2 x 2 lím ‑--‑‑‑‑‑‑‑ = ----- = + oo x 2+ x 2 - 4 +0 pues x vale algo más de 2 y x 2 > 4 x 2 lím ‑‑‑‑ = ------ = - oo x 2 - x 2 - 4 -0 pues x vale algo menos de 2 y x 2 < 4 @ Angel Prieto Benito Apuntes 1º Bachillerato CT -2 0 2 x 16

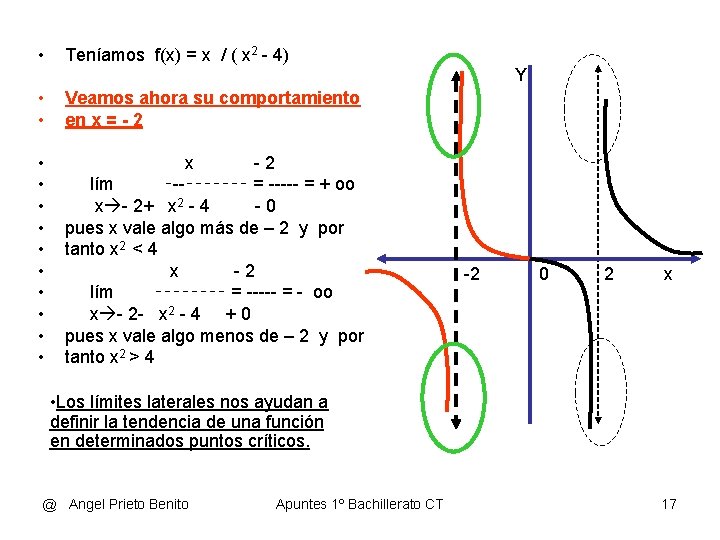
• Teníamos f(x) = x / ( x 2 - 4) Y • • Veamos ahora su comportamiento en x = - 2 • • • x -2 lím ‑--‑‑‑‑‑‑‑ = ----- = + oo x - 2+ x 2 - 4 -0 pues x vale algo más de – 2 y por tanto x 2 < 4 x -2 lím ‑‑‑‑ = ----- = - oo x - 2 - x 2 - 4 + 0 pues x vale algo menos de – 2 y por tanto x 2 > 4 -2 0 2 x • Los límites laterales nos ayudan a definir la tendencia de una función en determinados puntos críticos. @ Angel Prieto Benito Apuntes 1º Bachillerato CT 17