Lesson 18 Ratio Word Problems Similar Triangles A

Lesson 18: Ratio Word Problems, Similar Triangles

A ratio is a comparison of two numbers that can be written as a fraction. If we write the fraction ¾ We say that we have written the ration of 3 to 4. all of the following ratios designate the same number and thus are equal ratios. ¾ 6/8 300/400 27/36

An equation or other statement that indicates that two ratios are equal is called a proportion. Thus, we say that ¾ = 15/20 Is a proportion.

We note that cross products of equal ratios are equal. ¾ = 15/20 3(20) = 4(15) 60 = 60

We can solve proportions that contain an unknown by setting the cross product equal and then dividing to complete the solution. 4/3 = 5/k 4 k = 15/4

When we set the cross products equal, we say that we have cross multiplied. In some ratio word problems the word ratio is used, but in other ratio word problems the word ratio is not used, and it is necessary to realize that a constant ratio is implied.

Example: The ratio of Arabians to mixed breeds in the herd was 2 to 17. if there were 380 horses in the herd, how many were Arabians?

Answer: 2/19 = A/380 40 Arabian Horses

Example: It took 600 kilograms of sulfur to make 3000 kg of the new compound. How many kg of other materials would be required to make 4000 kg of the new compound?

Answer: 2400/3000 = NS/4000 3200 kg of the new compound

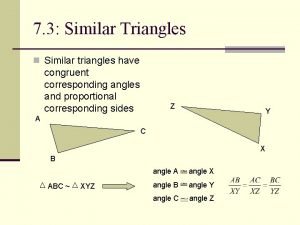
If two triangles have the same angles, the triangles have the same shape, and they look alike. We say that triangles that have the same angles are similar triangles.

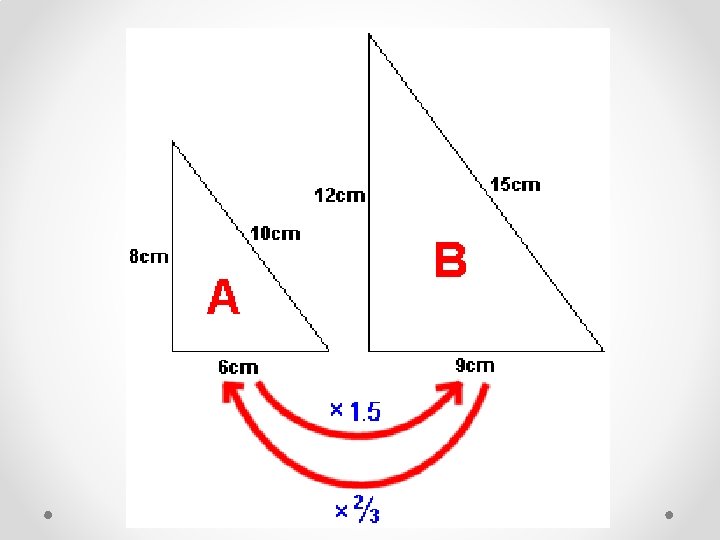
The sides opposite equal angles in similar triangles are called corresponding sides. The ratios of the lengths of corresponding sides in similar triangles are equal. This implies that corresponding sides in similar triangles are related by a number called the scale factor.

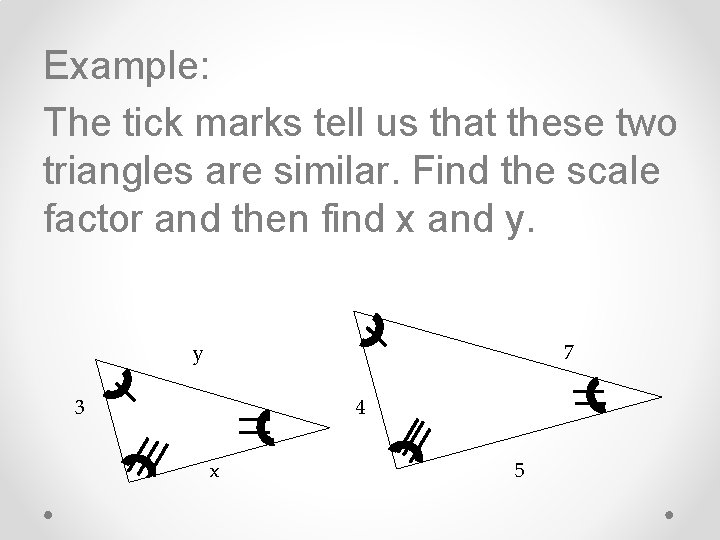
Example: The tick marks tell us that these two triangles are similar. Find the scale factor and then find x and y. y 7 3 4 x 5

Answer: Scale Factor = ¾ x = 15/4 y = 21/4

HW: Lesson 18 #1 -30