Lecture 5 Nonregular languages 2004 SDU Are all

Lecture 5 Non-regular languages 2004 SDU

Are all languages regular? Answer: No! One argument: § # of DFA’s on ? § # of languages on ? the latter is larger than the former. 2004 SDU

Pumping Lemma First technique to show that specific given languages are not regular. The idea: § Each regular language satisfies the pumping lemma, so, if a language does not, then, it is non-regular! 2004 SDU

Statement of Pumping Lemma If A is a regular language, then there is a number p (pumping length) where, if s is any string in A of length at least p, then s must be able to be divided into three pieces, s = xyz, satisfying the following conditions: 1. for each i 0, xyiz A, 2. |y| > 0, and 3. |xy| p. 2004 SDU

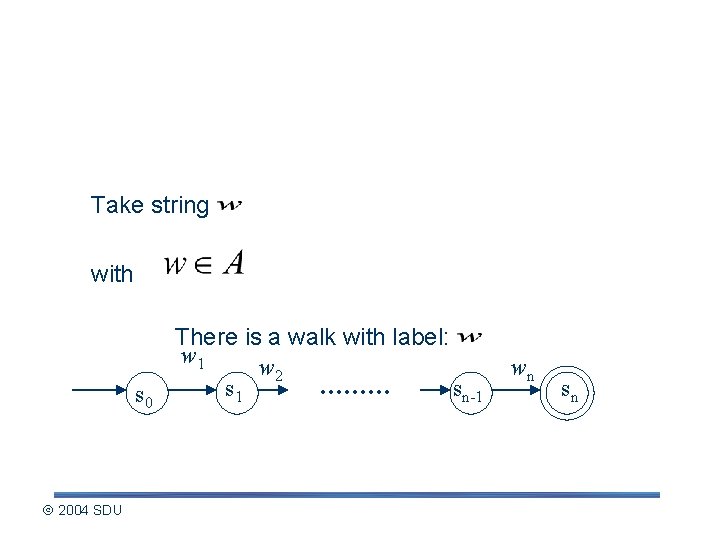
Describing the pumping lemma (contd. ) Take string with s 0 2004 SDU There is a walk with label: w 1 w 2. . s 1 sn-1 wn sn

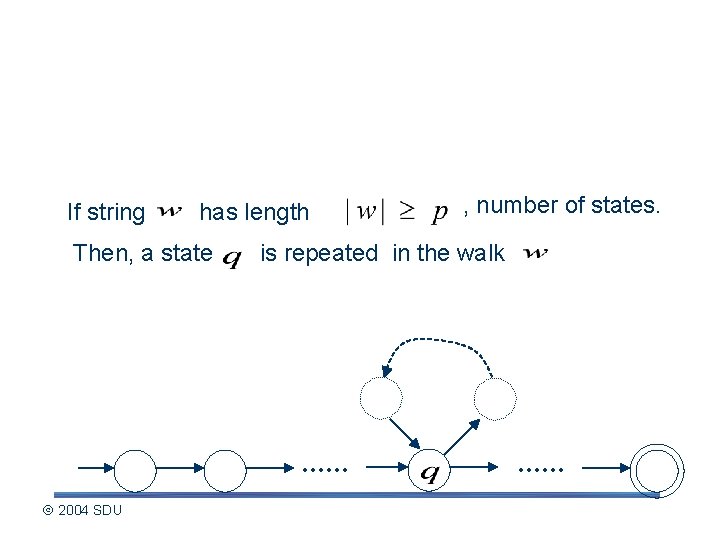
Describing the pumping lemma (contd. ) If string has length Then, a state is repeated in the walk . . . 2004 SDU , number of states. . . .

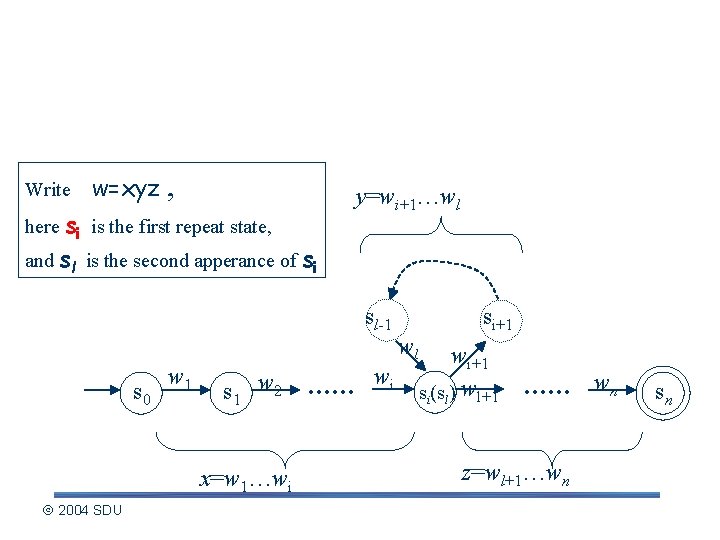
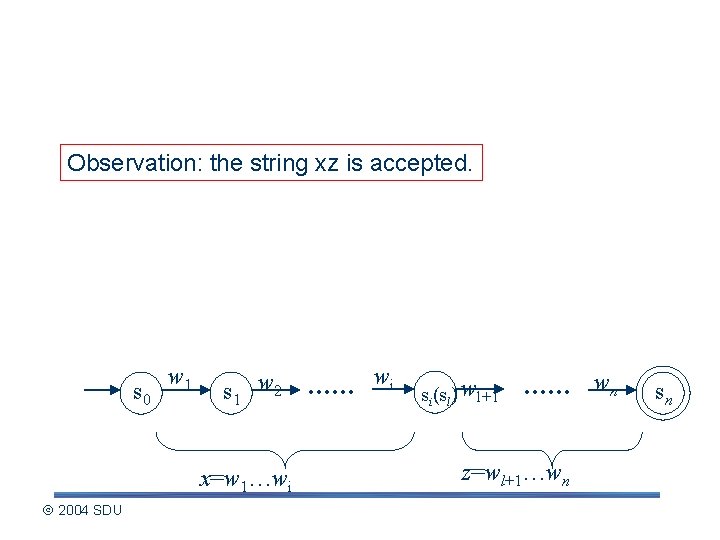
Describing the pumping lemma (contd. ) Write w=xyz , y=wi+1…wl here si is the first repeat state, and sl is the second apperance of si sl-1 s 0 w 1 s 1 w 2 x=w 1…wi 2004 SDU . . . wi wl si+1 wi+1 si(sl) wl+1 . . . z=wl+1…wn wn sn

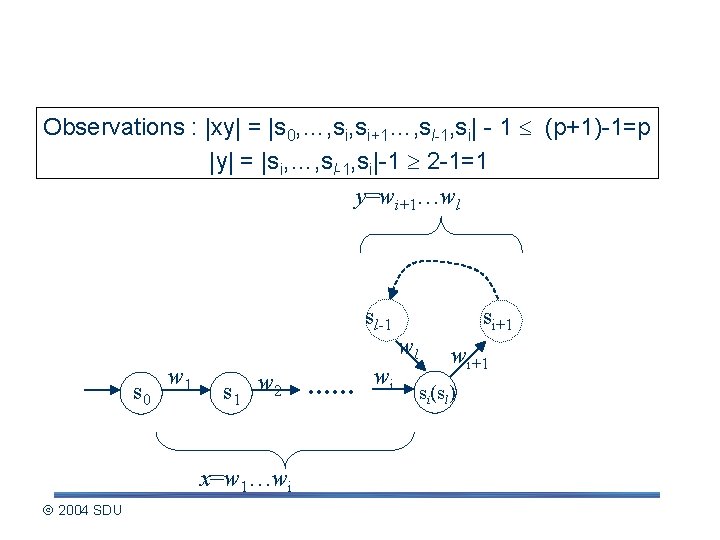
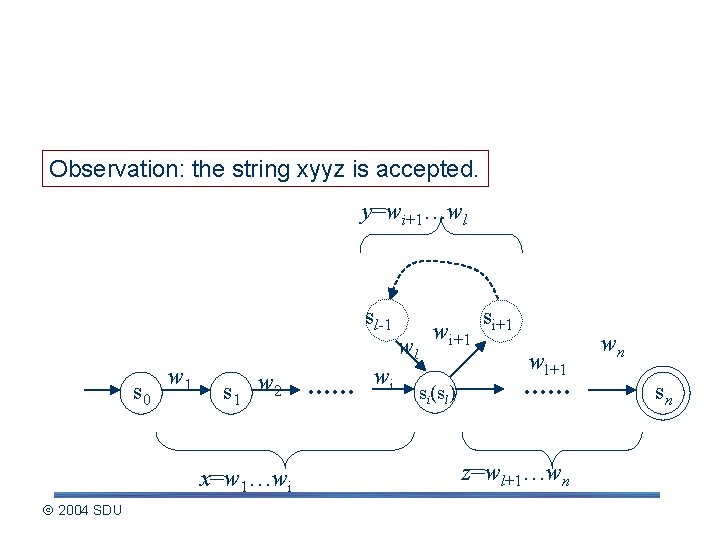
Describing the pumping lemma (contd. ) Observations : |xy| = |s 0, …, si+1…, sl-1, si| - 1 (p+1)-1=p |y| = |si, …, sl-1, si|-1 2 -1=1 y=wi+1…wl sl-1 s 0 w 1 s 1 w 2 x=w 1…wi 2004 SDU . . . wi wl si+1 wi+1 si(sl)

Describing the pumping lemma (contd. ) Observation: the string xz is accepted. s 0 w 1 s 1 w 2 x=w 1…wi 2004 SDU . . . wi si(sl) wl+1 . . . z=wl+1…wn wn sn

Describing the pumping lemma (contd. ) Observation: the string xyyz is accepted. y=wi+1…wl sl-1 s 0 w 1 s 1 w 2 x=w 1…wi 2004 SDU . . . wi wl wi+1 si(sl) si+1 wl+1 . . . z=wl+1…wn wn sn

Proof of pumping lemma Idea: If a string w of length m is accepted by a DFA with p states, and m p, then there is a repeat state (let i be the first one) in the accepting state sequence. z x y s 0 w 1 s 1…wisiwi+1 si+1…wlsl(=si)wl+1 sl+1…wmsm • |xy| = |w 1, …, wl| = |s 0, …, si+1, …, si| - 1 (p+1)-1 = p • |y| = |wi+1, …, wl | = |si, si+1, …, si| - 1 2 -1=1 • xz (= w 1…wiwl+1…wm): s 0, …, si, sl+1, …, sm • xyyz( = w 1…wiwi+1…wlwl+1…wm): s 0, …, si+1, . . , sl, si+1, …, sl+1, …, sm 2004 SDU

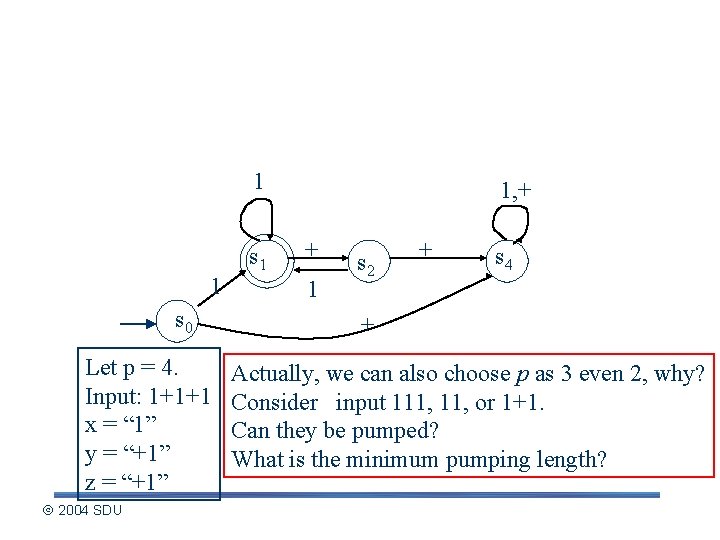
An exmaple 1 1 s 0 Let p = 4. Input: 1+1+1 x = “ 1” y = “+1” z = “+1” 2004 SDU s 1 1, + + 1 s 2 + s 4 + Actually, we can also choose p as 3 even 2, why? Consider input 111, or 1+1. Can they be pumped? What is the minimum pumping length?

Application of Pumping Lemma Example 1: A = { 0 n 1 n | n 0} is not regular. Proof. By contradiction. Assume, on the contrary, that A is regular. Then the pumping lemma holds for A. Let p be a pumping length. Let w = 0 p 1 p. Then w is in A and is longer than p. Then by pumping Lemma, w can be divided into w=xyz such that • For each i 0, xyiz A • |y| > 0, and 0000 1111 y • |xy| p. Then x and y are all 0’s. So, xyyz has more 0’s than 1’s and is in A. A contradiction. So, A is not regular. 2004 SDU

Application of Pumping Lemma Example 2: B={ w | w {0, 1}* and has an equal number of 0’s and 1’s} is not regular. Proof. By contradiction. Assume, on the contrary, that B is regular. Then the pumping lemma holds for B. Let p be a pumping length. Let w = 0 p 1 p. Then w is in B and is longer than p. Then by pumping Lemma, w can be divided into w=xyz such that • For each i 0, xyiz B • |y| > 0, and • |xy| p. Then x and y are all 0’s. So, xyyz has more 0’s than 1’s and is in B. A contradiction. So, B is not regular. Another proof. Let B’=B 0*1*. If B is regular, then B’=A is regular, a contradiction. 2004 SDU

Application of Pumping Lemma Example 3: C = {ww | w {0, 1}*} is not regular. Proof. By contradiction. Assume, on the contrary, that C is regular. Then the pumping lemma holds for C. Let p be a pumping length. Let w = 0 p 1. Then w is in C and is longer than p. Then by pumping Lemma, w can be divided into w=xyz such that • For each i 0, xyiz C • |y| > 0, and • |xy| p. Then x and y are all 0’s. Obviously xyyz cannot be represented as ww. A contradiction to that xyyz C. So, C is not regular. 2004 SDU

Application of Pumping Lemma Example 4: D={1 a | a = n 2 for some n 0} is not regular. Proof. By contradiction. Assume, on the contrary, that D is regular. Then the pumping lemma holds for D. Let p be a pumping length. Let w = 1 b, b=p 2. Then w is in D and is longer than p. Then by pumping Lemma, w can be divided into w=xyz such that • For each i 0, xyiz D • |y| > 0, and • |xy| p. Then xyyz=1 c, where p 2 < c = p 2 + |y| p 2 + p, then c cannot be expressed as n 2 for any n. A contradiction to that xyyz D. So, D is not regular. 2004 SDU

Application of Pumping Lemam Example 5: E={0 i 1 j | i > j} is not regular. Proof. By contradiction. Assume, on the contrary, that E is regular. Then the pumping lemma holds for E. Let p be a pumping length. Let w = 0 p 1 p-1. Then w is in E and is longer than p. Then by pumping Lemma, w can be divided into w=xyz such that • For each i 0, xyiz E • |y| > 0, and • |xy| p. Then both x and y are strings of all 0’s. Then xz = 0 x 1 p-1, where x p-1. A contradiction to that xz E. So, E is not regular. 2004 SDU