Today Chapter 1 RE Regular Languages nonregular languages

Today • Chapter 1: • RE = Regular Languages, • nonregular languages • RL pumping lemma • Chapter 2: • Context-Free Languages (CFLs)

Regular Expressions (Def. 1. 26) Given an alphabet , R is a regular expression if: 1. 2. 3. 4. 5. 6. R = a, with a R= R= R = (R 1 R 2), with R 1 and R 2 regular expressions R = (R 1*), with R 1 a regular expression

Thm 1. 28: RL ~ RE We need to prove both ways: • If a language is described by a regular expression, then it is regular (Lemma 1. 29) (Last week we saw how we can convert a regular expression R into an NFA M such that L(R)=L(M)) • Today we do the second part: If a language is regular, then it can be described by a regular expression (Lemma 1. 32)

Generalized NFA Generalized nondeterministic finite automaton M=(Q, , , qstart, qaccept) with • Q finite set of states • the input alphabet • qstart the start state • qaccept the accept state • : (Q{qaccept}) (Q{qstart}) R the transition function • (R is the set of regular expressions over )

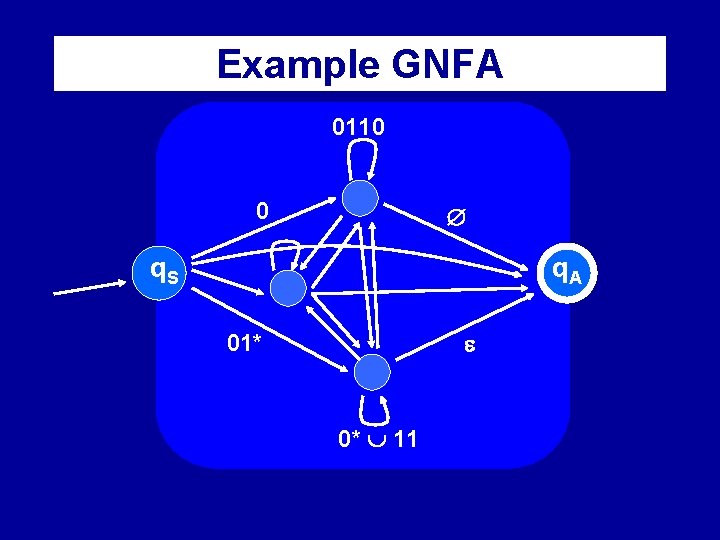
Example GNFA 0110 0 q. S q. A 01* 0* 11

Characteristics of GNFA’s • : (Q{qaccept}) (Q{qstart}) R The interior Q{qaccept, qstart} is fully connected by From qstart only ‘outgoing transitions’ To qaccept only ‘ingoing transitions’ Impossible qi qj transitions are “ (qi, qj) = ” Observation: This GNFA: recognizes the language L(R) q. S R R q. A

Proof Idea of Lemma 1. 32 Proof idea (given a DFA M): Construct an equivalent GNFA M’ with k 2 states Reduce one-by-one the internal states until k=2 This GNFA will be of the form This regular expression R will be such that L(R) = L(M) q. S R q. A

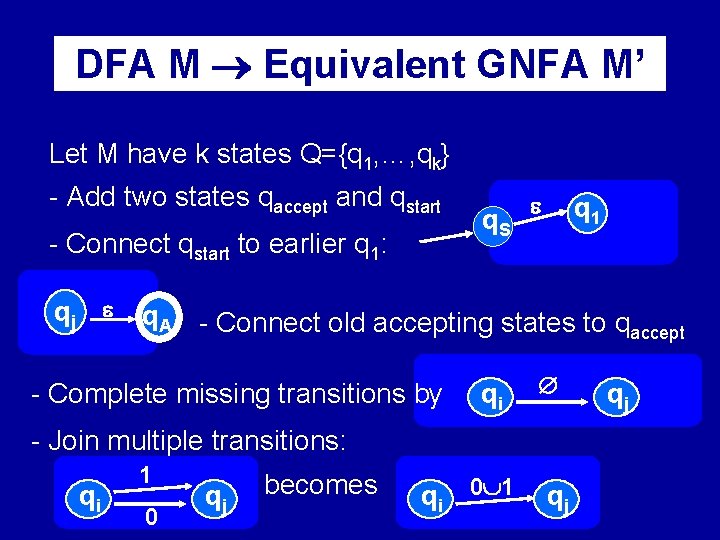
DFA M Equivalent GNFA M’ Let M have k states Q={q 1, …, qk} - Add two states qaccept and qstart - Connect qstart to earlier q 1: qj q. S q 1 q. A - Connect old accepting states to q accept - Complete missing transitions by qi - Join multiple transitions: qi 1 0 qj becomes qi 0 1 qj qj

Remove Internal state of GNFA If the GNFA M has more than 2 states, ‘rip’ internal qrip to get equivalent GNFA M’ by: - Removing state qrip: Q’=Q{qrip} - Changing the transition function by ’(qi, qj) = (qi, qj) ( (qi, qrip)( (qi, qj))* (qrip, qj)) for every qi Q’{qaccept} and qj Q’{qstart} qi R 1 q rip R 4 R 2 R 3 qj = qi R 4 (R 1 R 2*R 3) qj

Proof Lemma 1. 32 Let M be DFA with k states Create equivalent GNFA M’ with k+2 states Reduce in k steps M’ to M’’ with 2 states The resulting GNFA describes a single regular expressions R The regular language L(M) equals the language L(R) of the regular expression R

Recap Regular Languages = Regular Expressions Let R be a regular expression, then there exists an NFA M such that L(R) = L(M) The language L(M) of a DFA M is equivalent to a language L(M’) of a GNFA = M’, which can be converted to a two-state M’’ The transition qstart R qacceptof M’’ obeys L(R) = L(M’’) Hence: RE NFA = DFA GNFA RE

Nonregular Languages § 1. 4 Which languages cannot be recognized by finite automata? Example: L={ 0 n 1 n | n N } • ‘Playing around’ with FA convinces you that the ‘finiteness’ of FA is problematic for “all n N” • The problem occurs between the 0 n and the 1 n • Informal: the memory of a FA is limited by the number of states |Q|

Repeating DFA Paths Consider an accepting DFA M with size |Q| On a string of length p, p+1 states get visited For p |Q|, there must be a j such that the computational path looks like: q 1, …, qj, …, qk qj q 1 qk

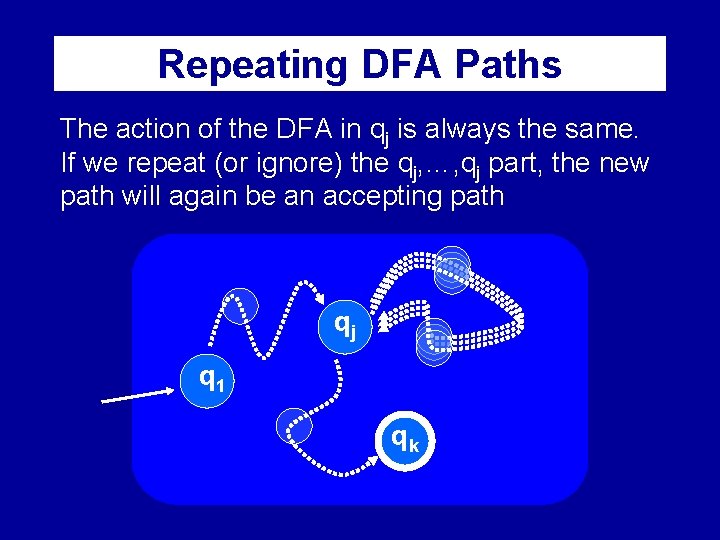
Repeating DFA Paths The action of the DFA in qj is always the same. If we repeat (or ignore) the qj, …, qj part, the new path will again be an accepting path qj q 1 qk

Line of Reasoning Proof by contradiction: • Assume that L is regular • Hence, there is a DFA M that recognizes L • For strings of length |Q| the DFA M has to ‘repeat itself’ • Show that M will accept strings outside L • Conclude that the assumption was wrong Note that we use the simple DFA, not the more elaborate (but equivalent) NFA or GNFA

Pumping Lemma (Thm 1. 37) For every regular language L, there is a pumping length p, such that for any string s L and |s| p, we can write s=xyz with 1) x yi z L for every i {0, 1, 2, …} 2) |y| 1 3) |xy| p Note that 1) implies that xz L 2) says that y cannot be the empty string Condition 3) is not always used

Formal Proof of Pumping Lemma Let M = (Q, , , q 1, F) with Q = {q 1, …, qp} Let s = s 1…sn L(M) with |s| = n p Computational path of M on s is the sequence r 1, …, rn+1 Qn+1 with r 1 = q 1, rn+1 F and rt+1= (rt, st) for 1 t n Because n+1 p+1, there are two states such that rj = rk (with j<k and k p+1) Let x = s 1…sj– 1, y = sj…sk– 1, and z = sk…sn+1 x takes M from q 1=r 1 to rj, y takes M from rj to rj, and z takes M from rj to rn+1 F As a result: xyiz takes M from q 1 to rn+1 F (i 0)

Formal Proof of Pumping Lemma Let M = (Q, , , q 1, F) with Q = {q 1, …, qp} Let s = s 1…sn L(M) with |s| = n p Computational path of M on s is the sequence r 1, …, rn+1 Qn+1 with r 1 = q 1, rn+1 F and rt+1= (rt, st) for 1 t n Because n+1 p+1, there are two terms such that rj = rk (with j<k and k p+1) |y| 1 and |xy| p Let x = s 1…sj– 1, y = sj…sk– 1, and z = sk…sn+1 x takes M from q 1=r 1 to rj, y takes M from rj to rj, and z takes M from rj to rn+1 F As a result: xy M from q 1 to i {0, 1, 2, …} rn+1 F (i 0) x iyzi takes z L(M) for every

Pumping 0 n 1 n (Ex. 1. 38) Assume that B = {0 n 1 n | n 0} is regular Let p be the pumping length, and s = 0 p 1 p B P. L. : s = xyz = 0 p 1 p, with xyiz B for all i 0 Three options for y: 1) y=0 k, hence xyyz = 0 p+k 1 p B 2) y=1 k, hence xyyz = 0 p 1 k+p B 3) y=0 k 1 l, hence xyyz = 0 p 1 l 0 k 1 p B Conclusion: The pumping lemma does not hold, the language B is not regular.

F = { ww | w {0, 1}* } (Ex. 1. 40) Let p be the pumping length, and take s = 0 p 1 Let s = xyz = 0 p 1 with condition 3) |xy| p Only one option: y=0 k, with xyyz = 0 p+k 10 p 1 F Without 3) this would have been a pain.

Intersecting Regular Languages Let C = { w | # of 0 s in w equals # of 1 s in w} Problem: If xyz C with y C, then xyiz C Idea: If C is regular and F is regular, then the intersection C F has to be regular as well Solution: Assume that C is regular Take the regular F = { 0 n 1 m | n, m N}, then for the intersection: C F = { 0 n 1 n | n N } But we know that C F is not regular Conclusion: C is not regular

Pumping Down E = { 0 i 1 j | i j } Problem: ‘pumping up’ s=0 p 1 p with y=0 k gives xyyz = 0 p+k 1 p, xy 3 z = 0 p+2 k 1 p, which are all in E (hence do not give contradictions) Solution: pump down to xz = 0 p–k 1 p. Overall for s = xyz = 0 p 1 p (with |xy| p): y=0 k, hence xz = 0 p–k 1 p E Contradiction: E is not regular End Chapter One