Properties of Regular Languages Chapter 4 Regular Languages

















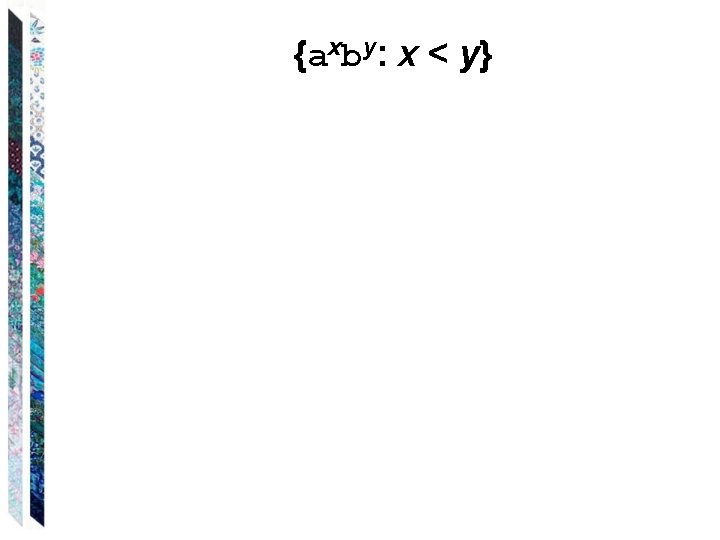

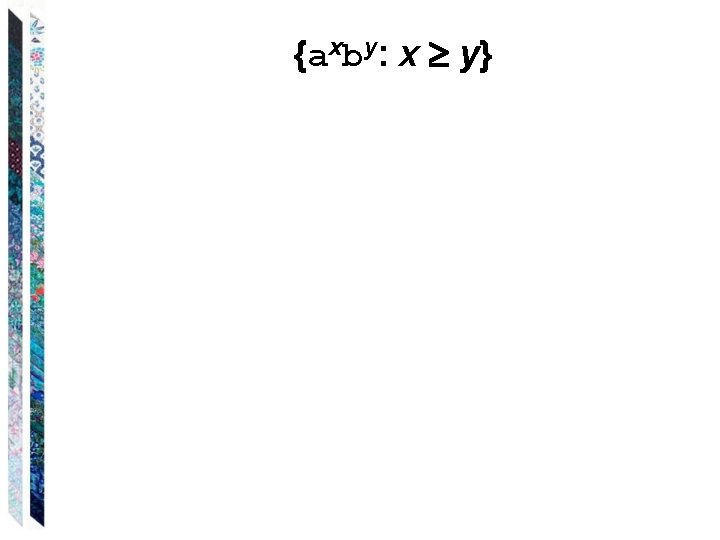


- Slides: 23

Properties of Regular Languages Chapter 4

Regular Languages A language is regular iff it is accepted by some DFA. Example: L = {w {a, b}* : every a is immediately followed by a b}.

Languages: Regular or Not? a*b* is regular. {anbn: n 0} is not. {w {a, b}* : every a is immediately followed by b} is regular. {w {a, b}* : every a has a matching b somewhere} is not Note: We may define a grammar for a non-regular language, but not a regular grammar (left- or right-linear)

Closure Properties of Regular Languages ● Union ● Intersection ● Concatenation ● Difference ● Kleene ● Reverse star ● Complement ● Letter substitution

Showing that a Language is Regular Theorem: Every finite language is regular. Proof: If L is the empty set, then it is defined by the regular expression and so is regular. If it is any finite language composed of the strings s 1, s 2, … sn for some positive integer n, then it is defined by the regular expression: s 1 + s 2 + … + sn So it too is regular.

Showing that a Language is Regular Example: Let L = L 1 ∩ L 2, where: L 1 = {anbn, n 0}, and L 2 = {bnan, n 0} L 1 and L 2 are not regular, but L = λ, which is regular

More Examples = {w {0 - 9}*: w is the social security number of the current US president}. ● L 1 ● L 2 = {1 if Santa Claus exists and 0 otherwise} ● L 3 = {1 if God exists and 0 otherwise} Examples of finite languages. Even though they may be unknown (or debatable), the languages are finite; therefore regular.

Showing That L is Regular 1. Show that L is finite. 2. Exhibit an FSM for L. 3. Exhibit a regular expression for L. 4. Show that the number of equivalence classes of L is finite. 5. Exhibit a regular grammar for L. 6. Exploit the closure theorems.

Identifying Nonregular Languages Finite languages are regular, but what about infinite languages? ? ? Some are regular: a*b* Some are not: L = {anbn: n 0}

Pigeonhole Principle If n objects are put into m boxes, and if n > m, then at least one box must have more than 1 object in it. Indicates repetition is needed

Showing that a Language is Not Regular Every regular language can be accepted by some FSM. It can only use a finite amount of memory to record essential properties. The only way to generate/accept an infinite language with a finite description is to use: • Kleene star (in regular expressions), or • cycles (in automata). This forces some kind of simple repetitive cycle within the strings. Example: ab*a generates aba, abbba, abbbba, etc.

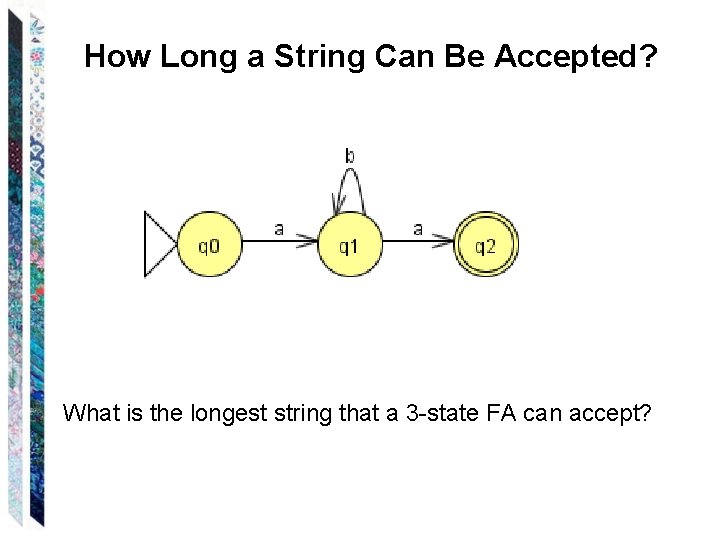
How Long a String Can Be Accepted? What is the longest string that a 3 -state FA can accept?

Theorem – Long Strings Theorem: Let M = (Q, , , q 0, F) be any DFSM. If M accepts any string of length |Q| or greater, then that string will force M to visit some state more than once (thus traversing at least one loop). Proof: M must start in one of its states. Each time it reads an input character, it visits some state. So, in processing a string of length n, M creates a total of n + 1 state visits. If n+1 > |Q|, then, by the pigeonhole principle, some state must get more than one visit. So, if n |Q|, then M must visit at least one state more than once.

The Pumping Lemma for Regular Languages Let L be an infinite regular language. So, m 1 : strings w L, where |w| m x, y, z w = xyz, |xy| m, |y| 1, and Note: m is the number of states in an FA that accepts L y represents a repetition in string w (a loop in the FA) i represents the number of times through the loop wi = xyi z is also in L, for all i = 0, 1, 2, …

The Pumping Lemma for Regular Languages Paraphrased: Every sufficiently long string in L can be broken into three parts in such a way that an arbitrary number of repetitions of the middle part yields another string in L. We say that the middle string is “pumped”.

Example: {anbn: n 0} is not Regular Choose w to be ambm (We get to choose any w; m is from pumping lemma). 1 2 aaaaa…aaaaabbbb …bbbbbb x y z We show that there is no x, y, z with the required properties: |xy| m, |y| 1, and wi = xyi z is also in L, for all i = 0, 1, 2, … Since |xy| m, y must be in region 1. So y = ap for some p 1. Assume that i = 2 (we pump one extra copy of y), this means: am+pbm which L, since it has more a’s than b’s.

Using the Pumping Theorem Effectively To choose w (a string in the language L): • Choose a w with as homogeneous as possible in initial region of length at least m. • Choose a w that is only barely in L. To choose i: • Try letting i be either 0 or 2. • If that doesn’t work, analyze L to see if there is some other specific value that will work.

Pal. Even = {ss. R : s {a, b}*} 1. Let w = ambmbmam Therefore, |w| = 4 m, |w| m. 2. w = xyz, where |xy| m and |y| 1; therefore y must occur in the first m characters, so y = ap, p > 0. 3. Let i = 2 (make an extra copy of y). This means that the first half of the string has more a’s than the second half of the string and is not in Pal. Even. Therefore, by contradiction of the pumping lemma, Pal. Even is not a regular language.
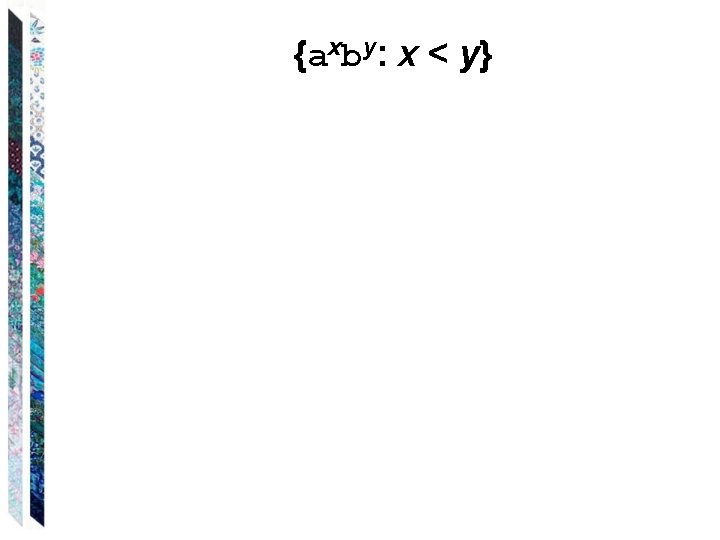
{axby: x < y}

L = {axby: x < y} Assume L is regular and m = # of states in the FA that accepts L: 1. Let w = ambm+1 Therefore, |w| = 2 m + 1, |w| m. 2. w = xyz, where |xy| m and |y| 1; therefore y must occur in the first m characters, so y = ap, p > 0. 3. Let i = 2 (make an extra copy of y). This means that the resulting string is am+p bm+1 Therefore, by contradiction of the pumping lemma, Pal. Even is not a regular language.
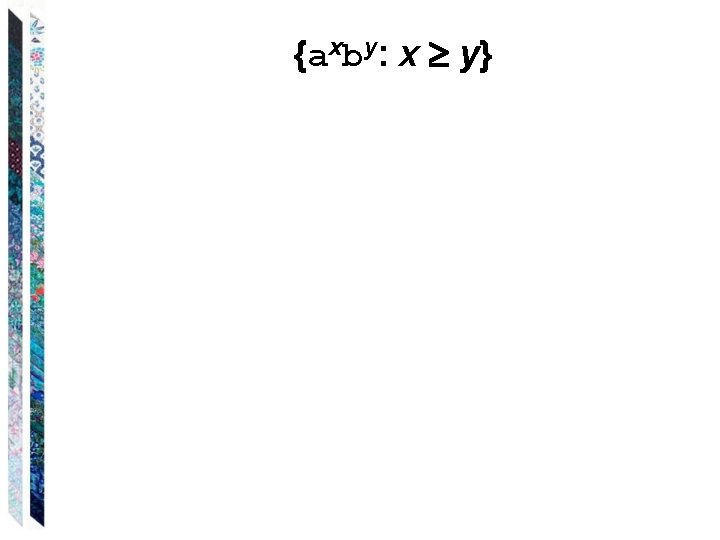
{axby: x y}

{axby: x y} Assume L is regular and m = # of states in the FA that accepts L: 1. Let w = ambm Therefore, |w| = 2 m, |w| m. 2. w = xyz, where |xy| m and |y| 1; therefore y must occur in the first m characters, so y = ap, p > 0. 3. Let i = 0 (pump out y). This means that the resulting string is am-p bm. Since p > 0, there are now fewer a’s than b’s. Therefore, by contradiction of the pumping lemma, Pal. Even is not a regular language.

Poetry The Pumping Lemma Any regular language L has a magic number p And any long-enough word in L has the following property: Amongst its first p symbols is a segment you can find Whose repetition or omission leaves x amongst its kind. So if you find a language L which fails this acid test, And some long word you pump becomes distinct from all the rest, By contradiction you have shown that language L is not A regular guy, resiliant to the damage you have wrought. But if, upon the other hand, x stays within its L, Then either L is regular, or else you chose not well. For w is xyz, and y cannot be null, And y must come before p symbols have been read in full. As mathematical postscript, an addendum to the wise: The basic proof we outlined here does certainly generalize. So there is a pumping lemma for all languages context-free, Although we do not have the same for those that are r. e. -- Martin Cohn