Lecture 8 NONContextfree languages 2004 SDU Are all

Lecture 8 NON-Context-free languages 2004 SDU

Are all languages context free? Ans: No. # of PDAs on < # of languages on Pumping lemma: A technique to show that specific given languages are not context free. 2004 SDU 2

Statement of Pumping Lemma Pumping lemma for context-free languages: If A is a context-free language, then there is a number p (the pumping length) where, if s is any string in A of length at least p, then s may be divided into five pieces s = uvxyz satisfying the uxz conditions. 1. For each i 0, uvixyiz A, 2. |vy| > 0, and 3. |vxy| p. 2004 SDU uvxyz uvvxyyz uvvvxyyyz uvvvvxyyyyz uvvvvvxyyyyyz 3

Proof of pumping lemma Idea: If a sufficiently long string s is derived by a CFG, then there is a repeated variable on a path in the parse tree. We can substitute the smaller sub-tree rooted at the lower occurrence for the larger sub-tree rooted at the higher. T. . occurrence to build infinitely many longer strings (and one shorter string, i = 0 case) derived by the CFG. R. . . R Think: why not use PDA to prove? 2004 SDU u v x y 4 z

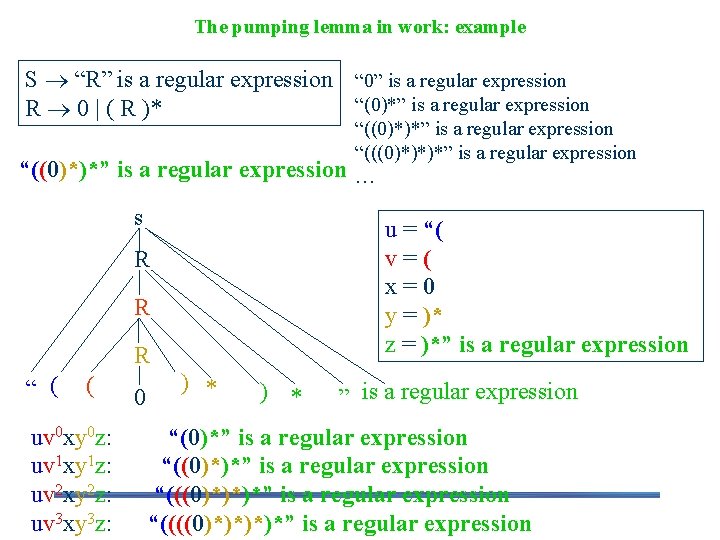
The pumping lemma in work: example S “R” is a regular expression “ 0” is a regular expression “(0)*” is a regular expression R 0 | ( R )* “((0)*)*” is a regular expression s u = “( v=( x=0 y = )* z = )*” is a regular expression R R R “ ( ( uv 0 xy 0 z: uv 1 xy 1 z: uv 2 xy 2 z: uv 3 xy 3 z: 0 “((0)*)*” is a regular expression “(((0)*)*)*” is a regular expression … ) * ” is a regular expression “(0)*” is a regular expression “((0)*)*” is a regular expression “(((0)*)*)*” is a regular expression “((((0)*)*” is a regular expression

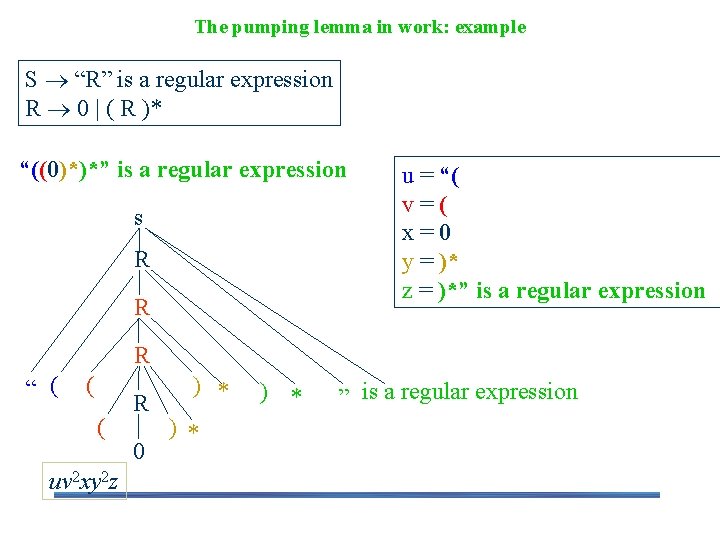
The pumping lemma in work: example S “R” is a regular expression R 0 | ( R )* “((0)*)*” is a regular expression s R R u = “( v=( x=0 y = )* z = )*” is a regular expression R “ ( ( ( uv 2 xy 2 z R 0 ) * ) * ” is a regular expression

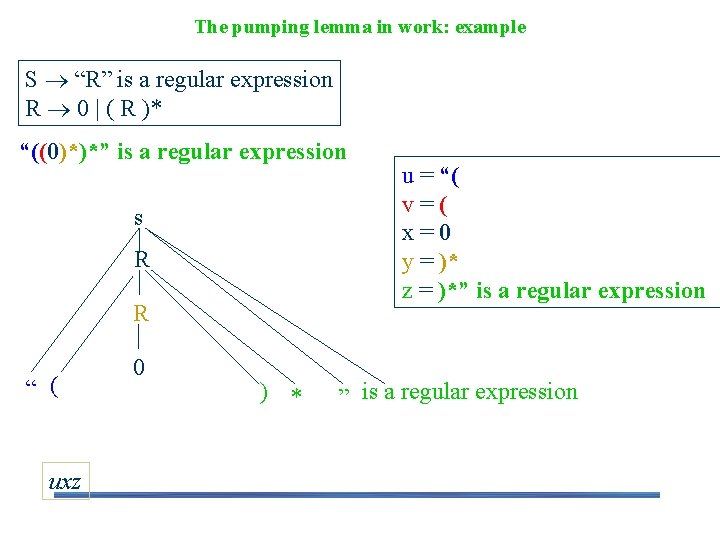
The pumping lemma in work: example S “R” is a regular expression R 0 | ( R )* “((0)*)*” is a regular expression s R R “ ( uxz 0 ) * u = “( v=( x=0 y = )* z = )*” is a regular expression

Details of Proof of Pumping Lemma How long does s have to be? § Let b be the maximum number of symbols in the righthand side of a rule. § Assume b 2. //why? – Each node in a parse tree using this grammar can have no more than b children. – At most b leaves are 1 step from the start variable; at most b 2 leaves are at most 2 steps from the start variable; at most bh leaves are at most h steps from the start variable. 2004 SDU 8

Details of Proof of Pumping Lemma (contd. ) So, if the height of the parse tree is at most h, the length of the string generated is at most bh § Let |V | = number of variables in G Set p = b|V|+1 § Because b 2, so a parse tree for any string in A of length at least p requires height at least |V | + 1. Therefore, let s in A be of length at least p. 2004 SDU 9

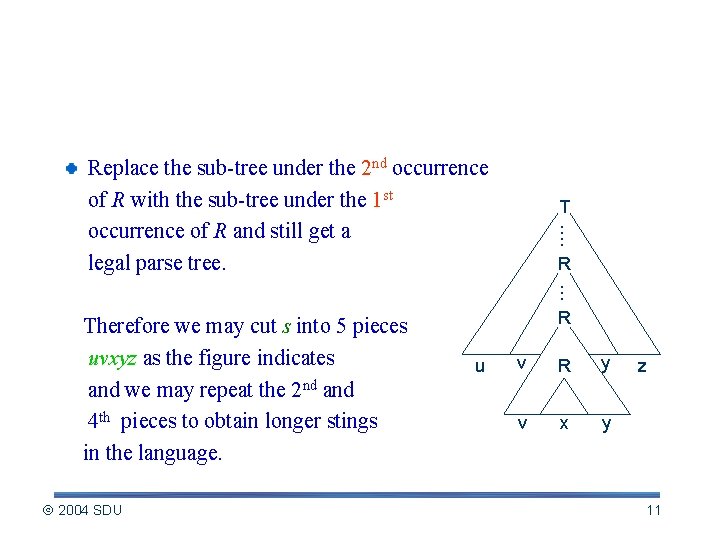
Details of Proof of Pumping Lemma (contd. ) Choose a parse tree T of s with smallest number of nodes. The longest path of T must have length |V| +1 Consider the lowest |V|+1 variables on this path. On this sub-path some variable R must repeat. T. . R u v x y z We start with a smallest parse tree that derives s 2004 SDU 10

Details of Proof of Pumping Lemma (contd. ) Replace the sub-tree under the 2 nd occurrence of R with the sub-tree under the 1 st occurrence of R and still get a legal parse tree. Therefore we may cut s into 5 pieces uvxyz as the figure indicates and we may repeat the 2 nd and 4 th pieces to obtain longer stings in the language. 2004 SDU T. . R u v R y v x y z 11

Details of Proof of Pumping Lemma (contd. ) In other words, uvixyiz is in A for any i 0. even if i = 0. For i=0, replace the sub-tree under the 1 st occurrence of R with the sub-tree under the 2 nd occurrence of R T. . R x u 2004 SDU z 12

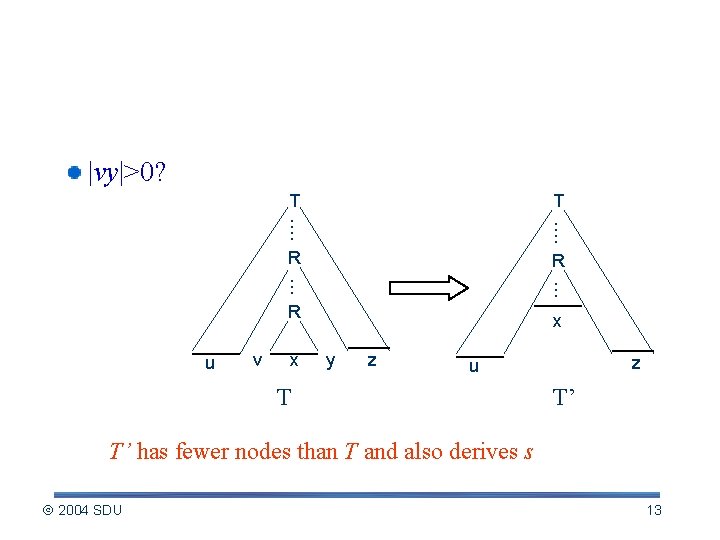
Details of Proof of Pumping Lemma (contd. ) |vy|>0? u v T. . . . R. . . R x x y z z u T T’ T’ has fewer nodes than T and also derives s 2004 SDU 13

Details of Proof of Pumping Lemma (contd. ) |vxy| p? Note that the sub-tree rooted at first R has height at most |V|+1, so, the string vxy has length at most p = b|V|+1. 2004 SDU 14

Application of pumping lemma A = {0 n 1 n 2 n| n 0} is not context free. Proof. Assume, on the contrary, that A is context free. By pumping lemma, there exists a constant p such that every w A of length p can be divided into w = uvxyz such that 1. |vxy| p 2. |vy| > 0 3. For every i 0, uvixyiz A. Let w = 0 p 1 p 2 p. Since |vxy| p, vxy is either in 0*1* or 1*2*. So, it is not the case that uv 2 xy 2 z has the same number of 0’s, 1’s as 2’s. 2004 SDU 15

Application of pumping lemma B = {ww | w {0, 1}*}is not context free. Proof. Assume B is context free. Let p be the constant from the pumping lemma for B. Let w = 0 p 1 p, which is in B. Then w can be written as w = uvxyz such that 1. |vxy| p 2. |vy| > 0 3. For every i 0, uvixyiz B. If v contains a symbol from the first 0 p, then y cannot contain one from the second 0 p, so pumping does not work. If v contains a symbol from the first 1 p, then y cannot contain one from the second 1 p, so, pumping lemma does not work. If v contains only symbols from the second 0 p 1 p, then pumping lemma does not work. 2004 SDU 16

C={0 n 1 n| n 0} is not context free. The proof is similar to that of B. Does this contradict that Context free languages are closed under concatenation? § C 1 = {0 n 1 n| n 0}, C 2 = {0 n 1 n| n 0}, § Is C = C 1 C 2 ? What happens if we change the stack to be first-in -first-out? Or use two first-in-last-out stacks? 2004 SDU 17