Lecture 12 Momentum Energy and Collisions Announcements EXAM

Lecture 12 Momentum, Energy, and Collisions

Announcements • EXAM: Thursday, October 17 (chapter 6 -9) • Equation sheet to be posted • Practice exam to be posted

Linear Momentum Impulse With no net external force:

Center of Mass The center of mass of a system is the point where the system can be balanced in a uniform gravitational field. For two objects: The center of mass is closer to the more massive object. Think of it as the “average location of the mass”

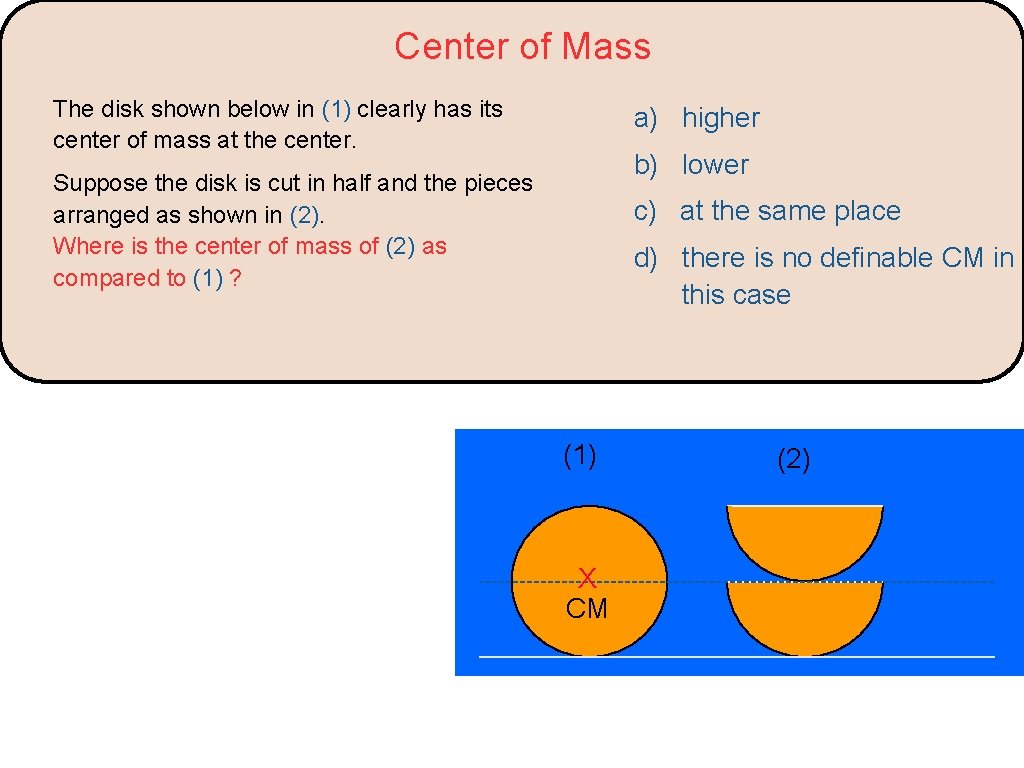
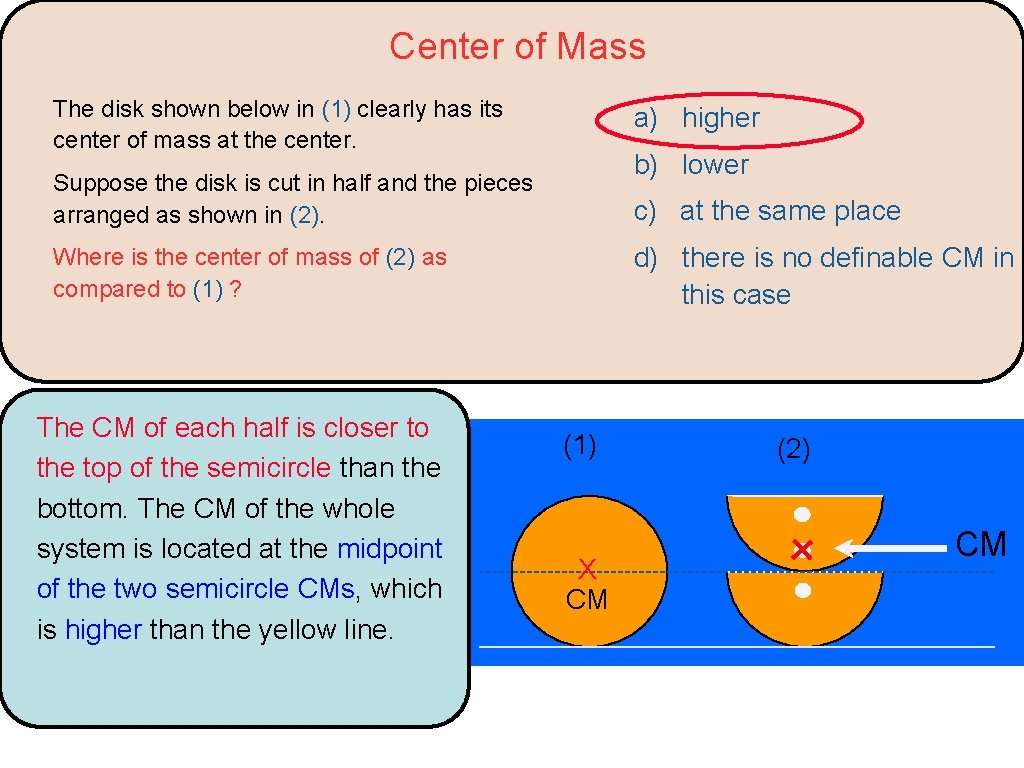
Center of Mass The disk shown below in (1) clearly has its center of mass at the center. a) higher b) lower Suppose the disk is cut in half and the pieces arranged as shown in (2). Where is the center of mass of (2) as compared to (1) ? c) at the same place d) there is no definable CM in this case (1) X CM (2)

Center of Mass The disk shown below in (1) clearly has its center of mass at the center. a) higher Suppose the disk is cut in half and the pieces arranged as shown in (2). c) at the same place b) lower d) there is no definable CM in this case Where is the center of mass of (2) as compared to (1) ? The CM of each half is closer to the top of the semicircle than the bottom. The CM of the whole system is located at the midpoint of the two semicircle CMs, which is higher than the yellow line. (1) X CM (2) CM

Gun Control When a bullet is fired from a gun, the bullet and the gun have equal and opposite momenta. If this is true, then why is the bullet deadly (whereas it is safe to hold the gun while it is fired)? a) it is much sharper than the gun b) it is smaller and can penetrate your body c) it has more kinetic energy than the gun d) it goes a longer distance and gains speed e) it has more momentum than the gun

Gun Control When a bullet is fired from a gun, the bullet and the gun have equal and opposite momenta. If this is true, then why is the bullet deadly (whereas it is safe to hold the gun while it is fired)? a) it is much sharper than the gun b) it is smaller and can penetrate your body c) it has more kinetic energy than the gun d) it goes a longer distance and gains speed e) it has more momentum than the gun Even though it is true that the magnitudes of the momenta of the gun and the bullet are equal, the bullet is less massive and so it has a much higher velocity. Because KE is related to v 2, the bullet has considerably more KE and therefore can do more damage on impact.

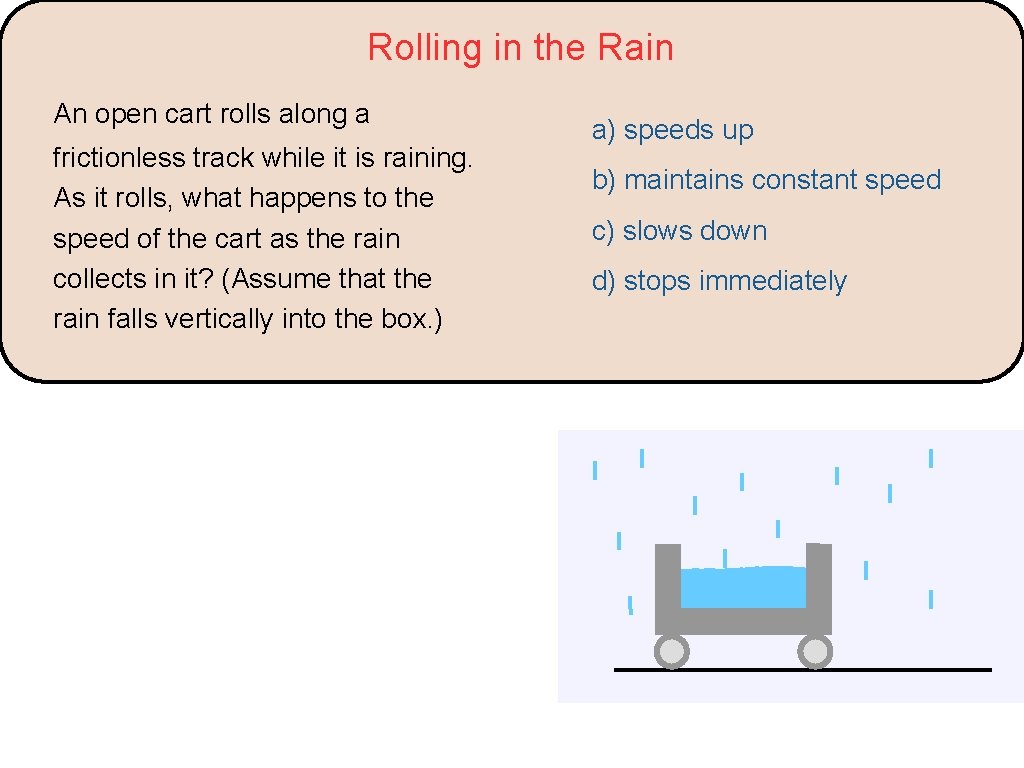
Rolling in the Rain An open cart rolls along a frictionless track while it is raining. As it rolls, what happens to the speed of the cart as the rain collects in it? (Assume that the rain falls vertically into the box. ) a) speeds up b) maintains constant speed c) slows down d) stops immediately

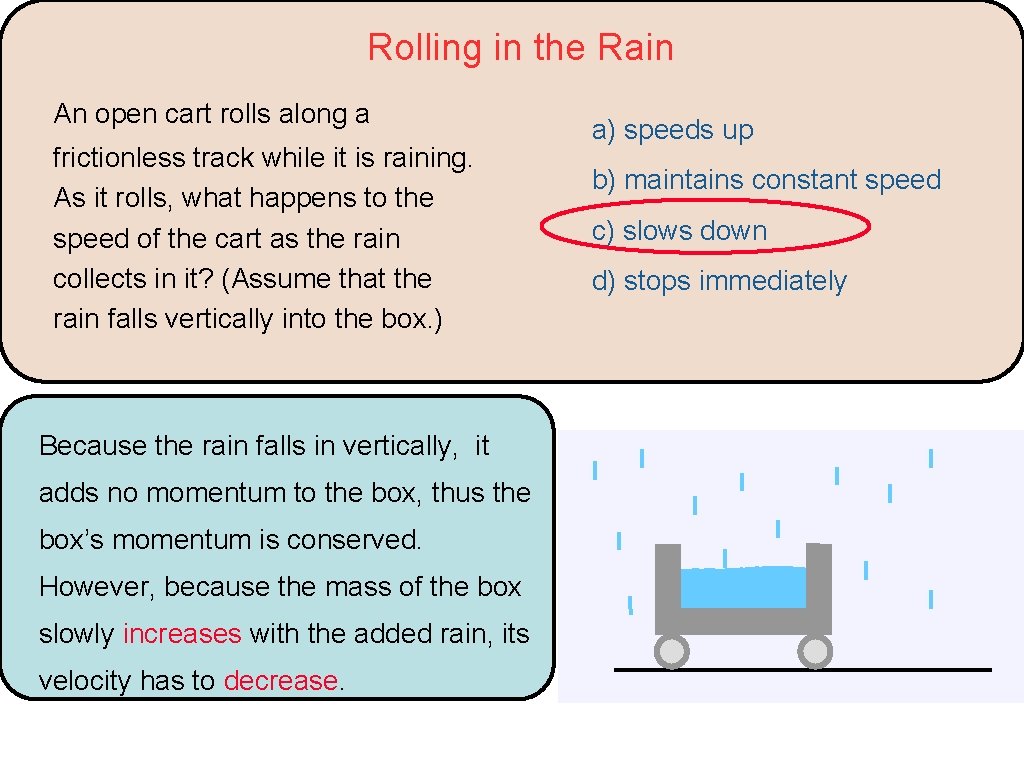
Rolling in the Rain An open cart rolls along a frictionless track while it is raining. As it rolls, what happens to the speed of the cart as the rain collects in it? (Assume that the rain falls vertically into the box. ) Because the rain falls in vertically, it adds no momentum to the box, thus the box’s momentum is conserved. However, because the mass of the box slowly increases with the added rain, its velocity has to decrease. a) speeds up b) maintains constant speed c) slows down d) stops immediately

Two objects collide. . . and stick mass m No external forces. . . so momentum of system is conserved initial px = mv 0 final px = (2 m)vf mv 0 = (2 m)vf vf = v 0 / 2 A completely inelastic collision: no “bounce back”

Inelastic collision: What about energy? mass m vf = v 0 / 2 initial final Kinetic energy is lost! KEfinal = 1/2 KEinitial

Collisions This is an example of an “inelastic collision” Collision: two objects striking one another Elastic collision ⇔ “things bounce back” ⇔ energy is conserved Inelastic collision: less than perfectly bouncy ⇔ Kinetic energy is lost Time of collision is short enough that external forces may be ignored so momentum is conserved Completely inelastic collision: objects stick together afterwards. Nothing “bounces back”. Maximal energy loss

Elastic vs. Inelastic Completely inelastic collision: colliding objects stick together, maximal loss of kinetic energy Inelastic collision: momentum is conserved but kinetic energy is not Elastic collision: momentum and kinetic energy is conserved.

Completely Inelastic Collisions in One Dimension Solving for the final momentum in terms of initial velocities and masses, for a 1 -dimensional, completely inelastic collision between unequal masses: Completely inelastic only (objects stick together, so have same final velocity) Momentum Conservation: KEfinal < KEinitial

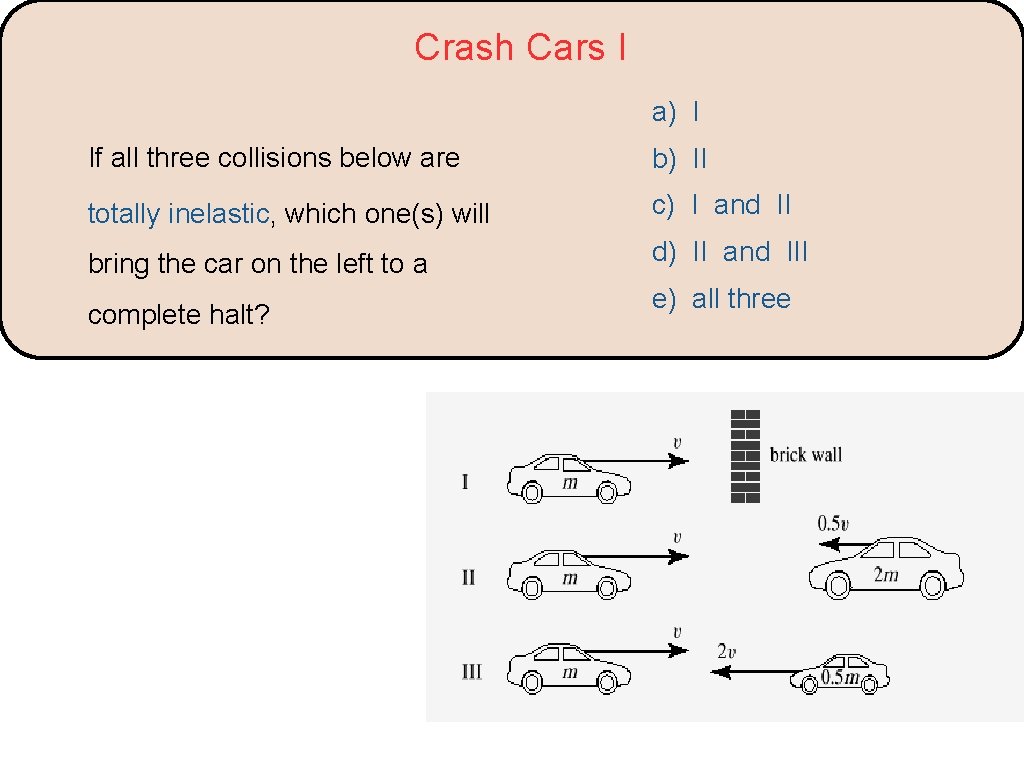
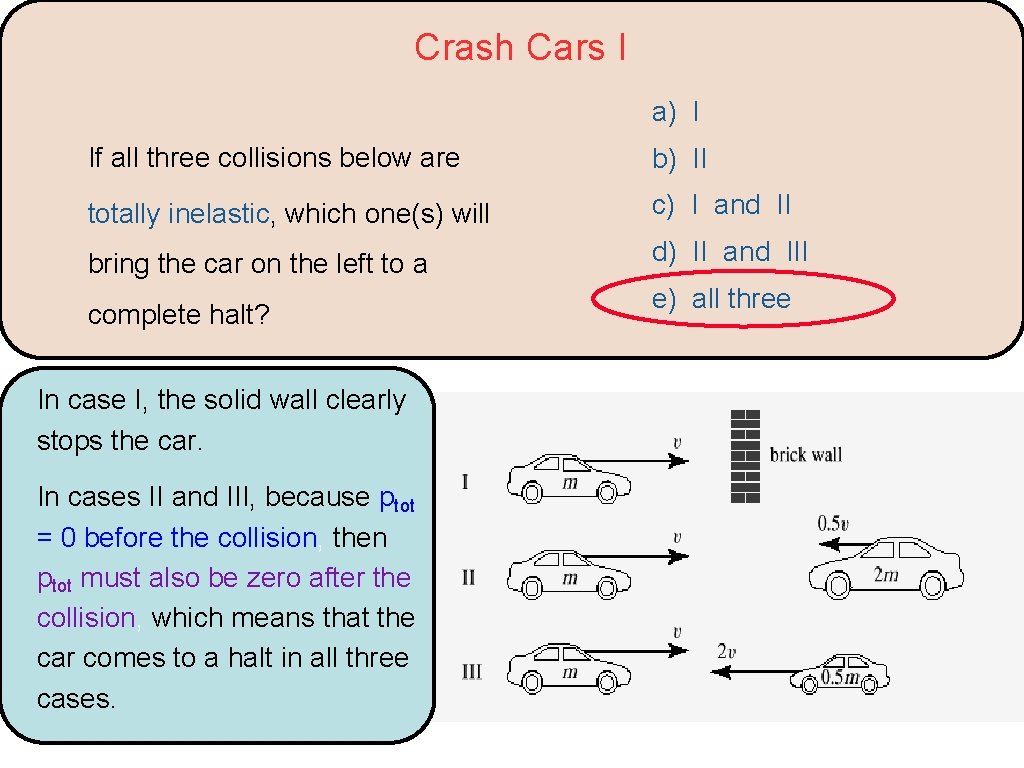
Crash Cars I a) I If all three collisions below are b) II totally inelastic, which one(s) will c) I and II bring the car on the left to a d) II and III complete halt? e) all three

Crash Cars I a) I If all three collisions below are b) II totally inelastic, which one(s) will c) I and II bring the car on the left to a d) II and III complete halt? In case I, the solid wall clearly stops the car. In cases II and III, because ptot = 0 before the collision, then ptot must also be zero after the collision, which means that the car comes to a halt in all three cases. e) all three

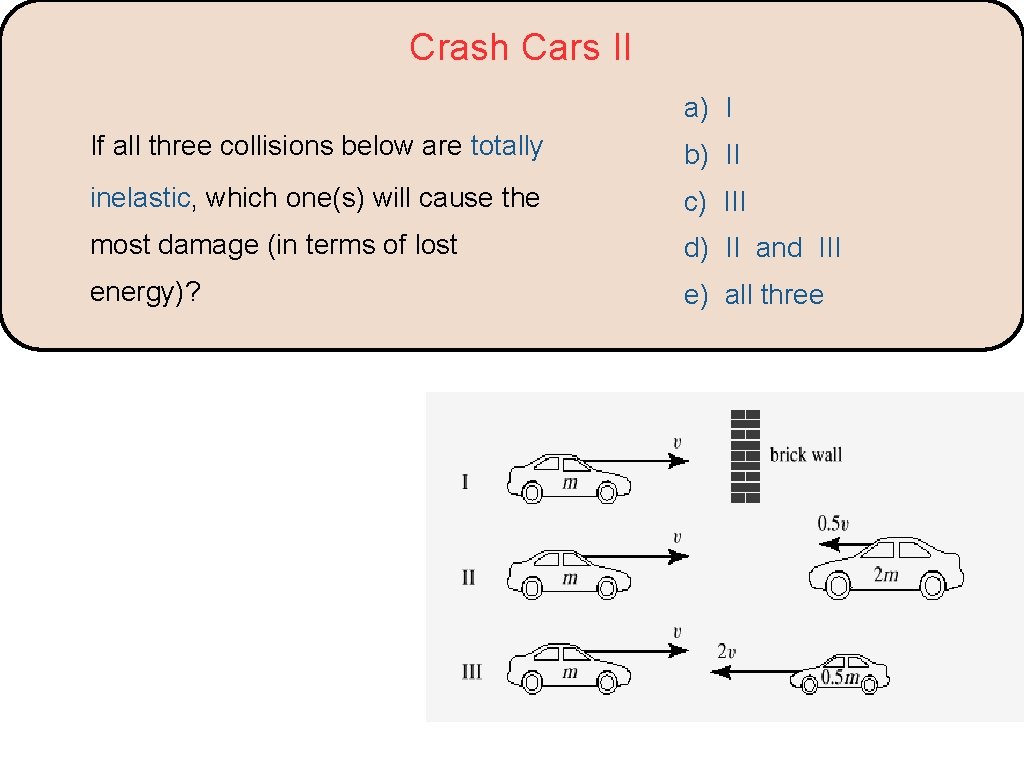
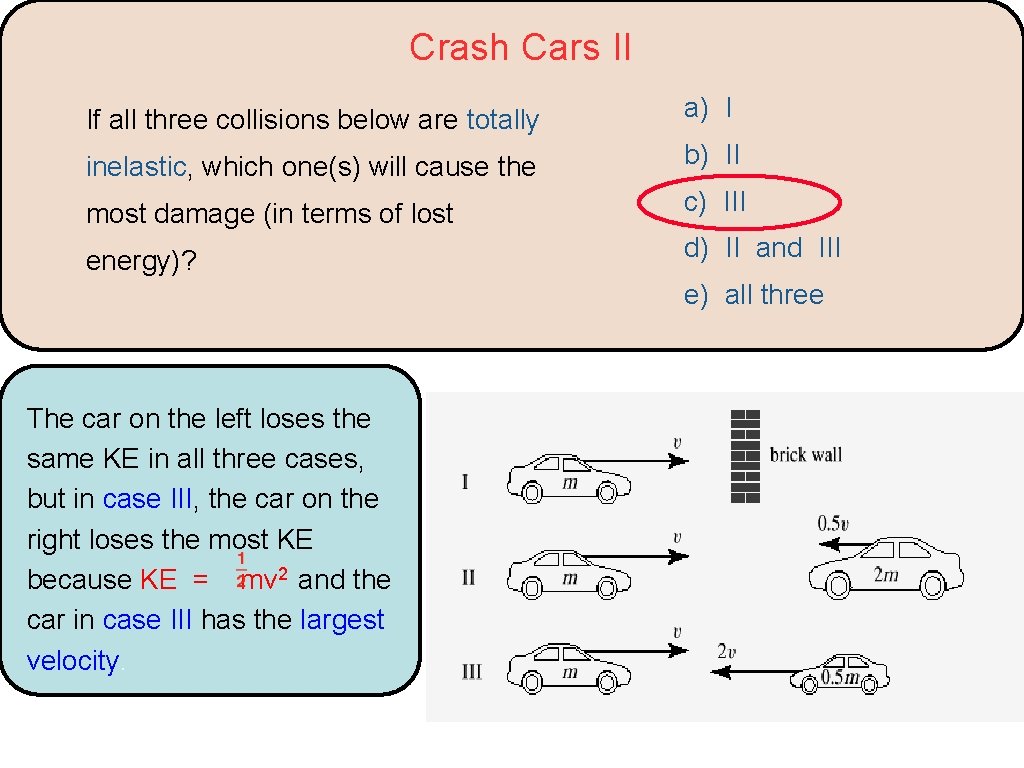
Crash Cars II a) I If all three collisions below are totally b) II inelastic, which one(s) will cause the c) III most damage (in terms of lost d) II and III energy)? e) all three

Crash Cars II If all three collisions below are totally a) I inelastic, which one(s) will cause the b) II most damage (in terms of lost c) III energy)? d) II and III e) all three The car on the left loses the same KE in all three cases, but in case III, the car on the right loses the most KE because KE = mv 2 and the car in case III has the largest velocity.

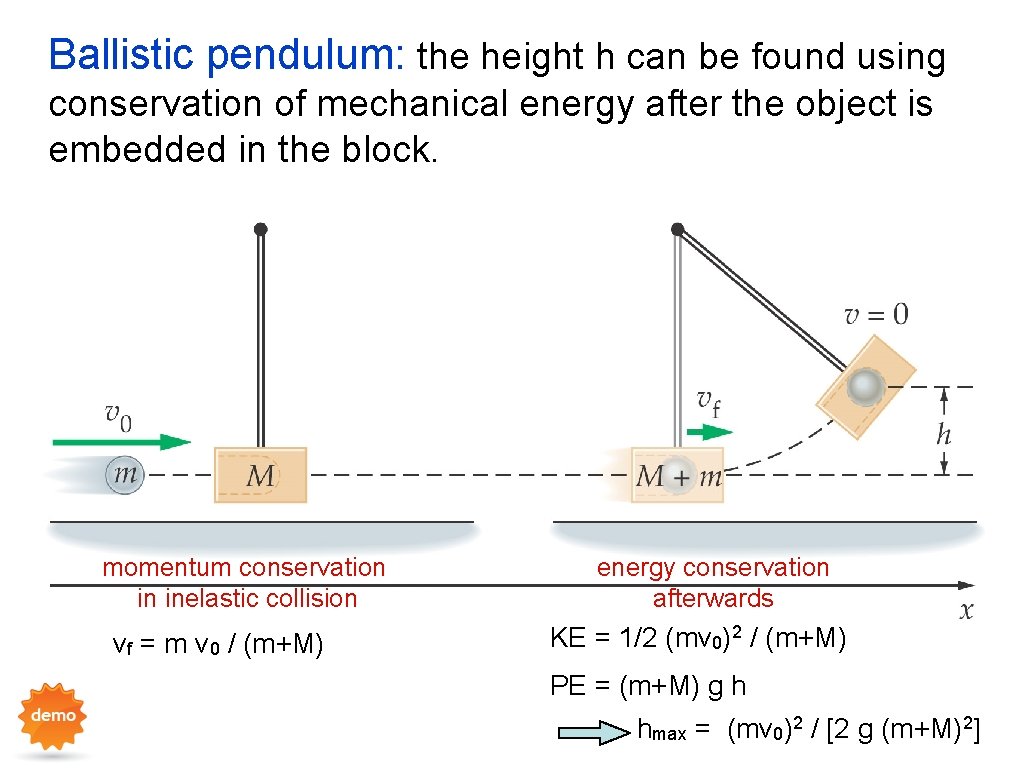
Ballistic pendulum: the height h can be found using conservation of mechanical energy after the object is embedded in the block. momentum conservation in inelastic collision vf = m v 0 / (m+M) energy conservation afterwards KE = 1/2 (mv 0)2 / (m+M) PE = (m+M) g h hmax = (mv 0)2 / [2 g (m+M)2]

Velocity of the ballistic pendulum approximation Pellet Mass (m): 2 g Pendulum Mass (M): 3. 81 kg Wire length (L): 4. 00 m

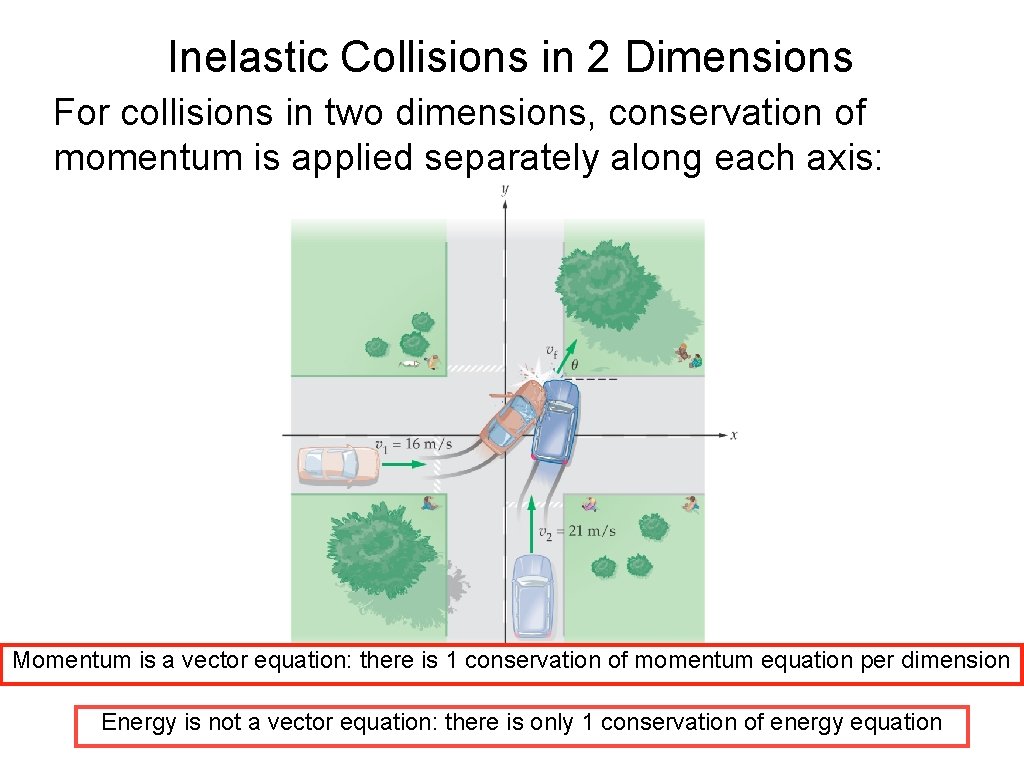
Inelastic Collisions in 2 Dimensions For collisions in two dimensions, conservation of momentum is applied separately along each axis: Momentum is a vector equation: there is 1 conservation of momentum equation per dimension Energy is not a vector equation: there is only 1 conservation of energy equation

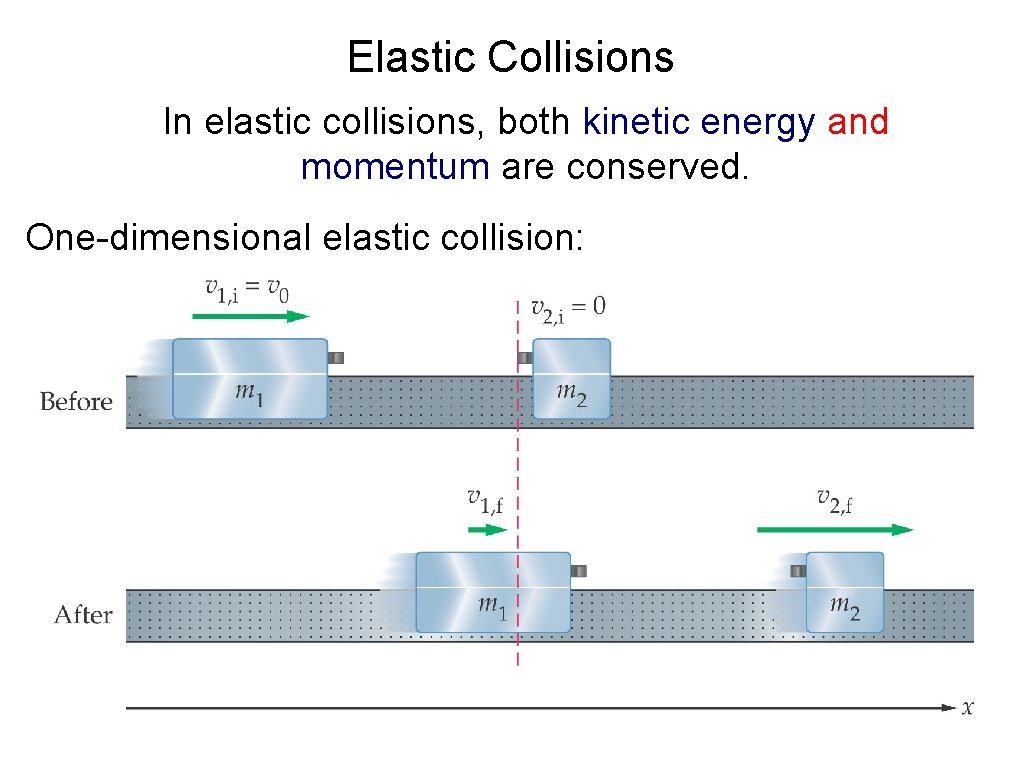
Elastic Collisions In elastic collisions, both kinetic energy and momentum are conserved. One-dimensional elastic collision:

Elastic Collisions in 1 -dimension For special case of v 2 i = 0 We have two equations: conservation of momentum conservation of energy and two unknowns (the final speeds). solving for the final speeds: Note: relative speed is conserved for head-on (1 -D) elastic collision

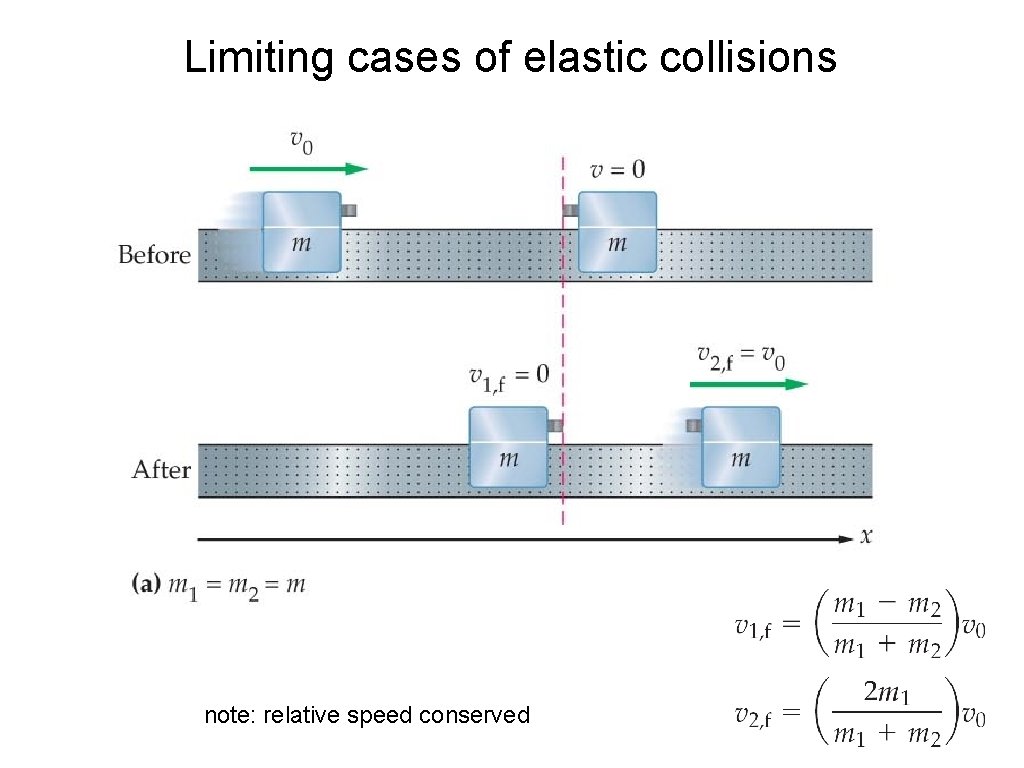
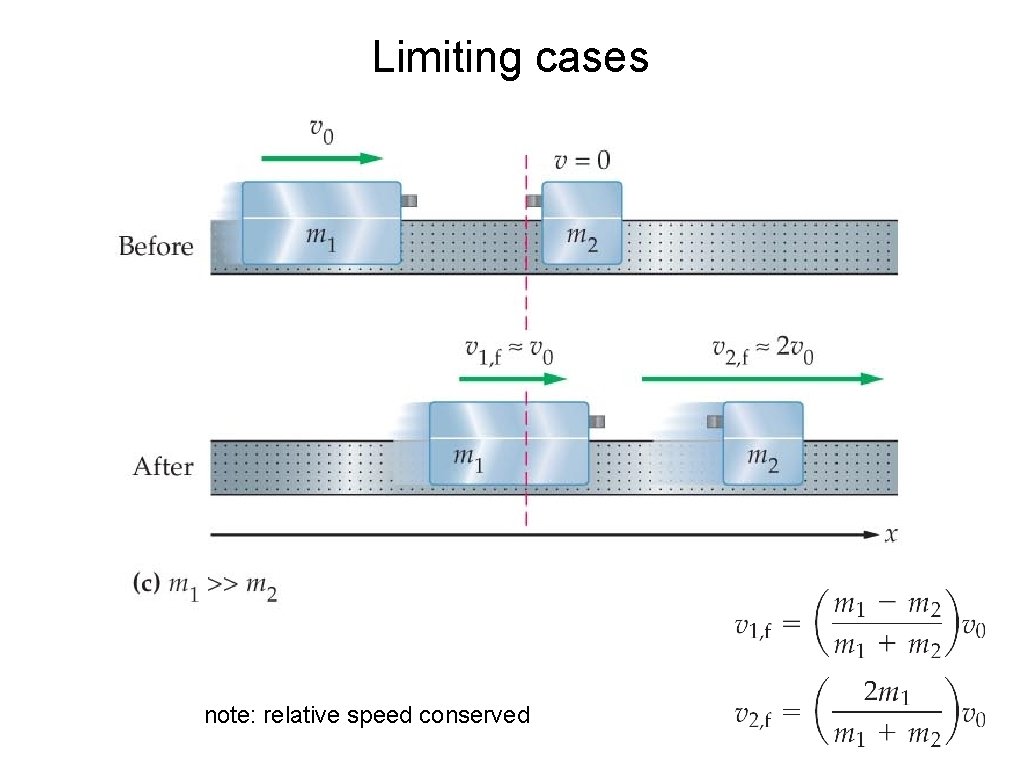
Limiting cases of elastic collisions note: relative speed conserved

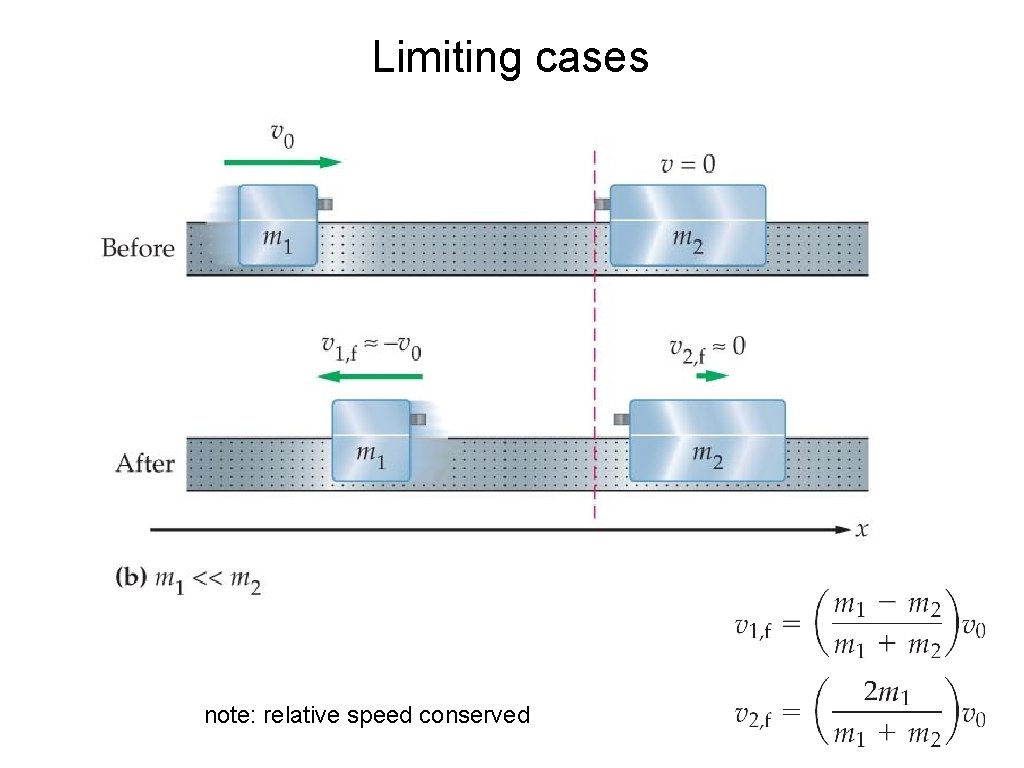
Limiting cases note: relative speed conserved

Limiting cases note: relative speed conserved

Toy Pendulum Could two balls recoil and conserve both momentum and energy? Incompatible!

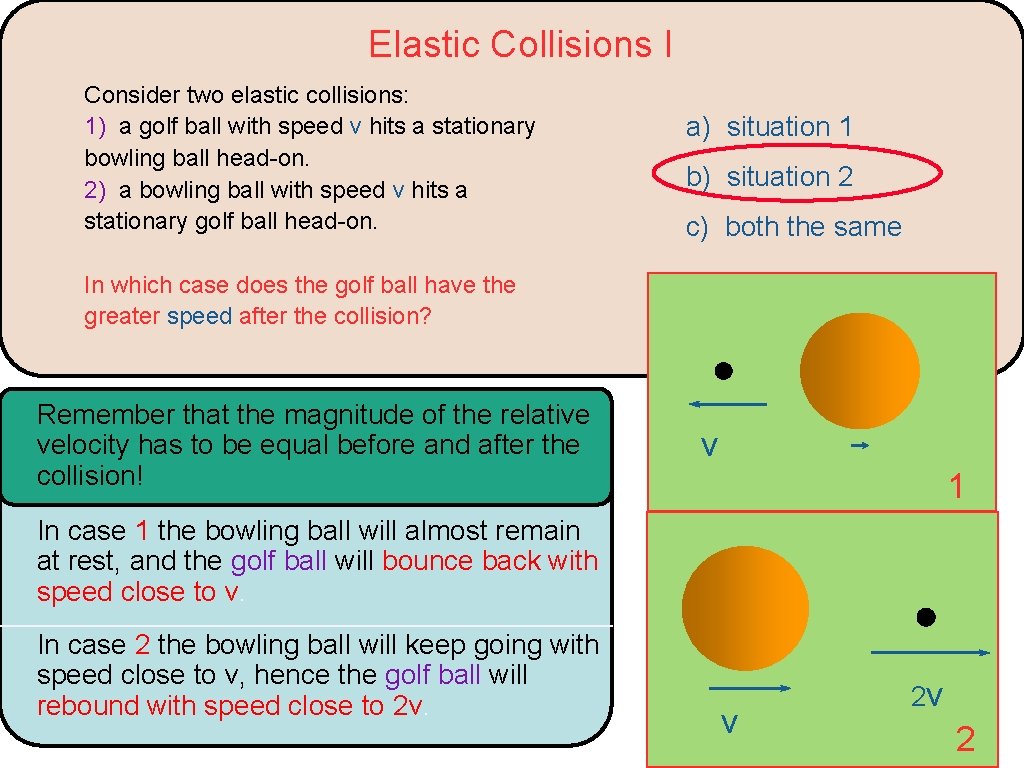
Elastic Collisions I Consider two elastic collisions: 1) a golf ball with speed v hits a stationary bowling ball head-on. 2) a bowling ball with speed v hits a stationary golf ball head-on. a) situation 1 b) situation 2 c) both the same In which case does the golf ball have the greater speed after the collision? v at rest 1 v 2

Elastic Collisions I Consider two elastic collisions: 1) a golf ball with speed v hits a stationary bowling ball head-on. 2) a bowling ball with speed v hits a stationary golf ball head-on. a) situation 1 b) situation 2 c) both the same In which case does the golf ball have the greater speed after the collision? Remember that the magnitude of the relative velocity has to be equal before and after the collision! v 1 In case 1 the bowling ball will almost remain at rest, and the golf ball will bounce back with speed close to v. In case 2 the bowling ball will keep going with speed close to v, hence the golf ball will rebound with speed close to 2 v. v 2 v 2

A charging bull elephant with a mass of 5240 kg comes directly toward you with a speed of 4. 55 m/s. You toss a 0. 150 kg rubber ball at the elephant with a speed of 7. 81 m/s. When the ball bounces back toward you, what is its speed?

A charging bull elephant with a mass of 5240 kg comes directly toward you with a speed of 4. 55 m/s. You toss a 0. 150 kg rubber ball at the elephant with a speed of 7. 81 m/s. When the ball bounces back toward you, what is its speed? Our simplest formulas for speed after an elastic collision relied on one body being initially at rest. So lets try a frame where one body (the elephant) is at rest! What is the speed of the ball relative to the elephant? In the frame, what is the final speed of the ball? Back in the frame of the ground:

A charging bull elephant with a mass of 5240 kg comes directly toward you with a speed of 4. 55 m/s. You toss a 0. 150 kg rubber ball at the elephant with a speed of 7. 81 m/s. When the ball bounces back toward you, what is its speed? Our simplest formulas for speed after an elastic collision relied on one body being initially at rest. So lets try a frame where one body (the elephant) is at rest! What is the speed of. Formulas the ball NOTE: relative to the elephant? for 1 -D elastic scattering with non-zero initial velocities are given in end In the frame, what is the final speed of 88. the ball? -of-chapter problem Back in the frame of the ground:

Elastic Collisions in 2 -D Two-dimensional collisions can only be solved if some of the final information is known, such as the final velocity of one object

CEBAF at JLab Precision hadronic microscopy CEBAF at Jefferson Lab • recirculation through continuouswave superconducting RF linacs • simultaneous beam delivery to 3 experimental halls with large complementary spectrometers • cold RF = stable, clean, quiet • up to 200 micro. Amps per hall, E~ 0. 5 -6 Ge. V, >80% polarization An ideal machine for precision hadronic microscopy! 3 experimental Halls First experiments begun in 1994 User community 1200 members strong

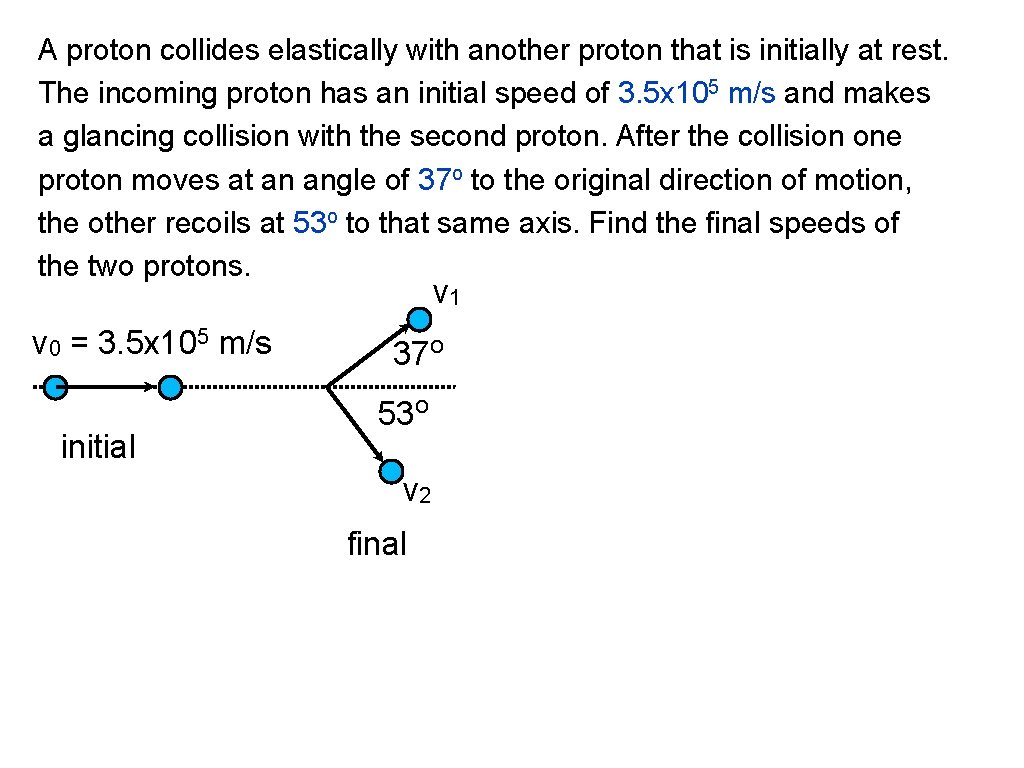
A proton collides elastically with another proton that is initially at rest. The incoming proton has an initial speed of 3. 5 x 105 m/s and makes a glancing collision with the second proton. After the collision one proton moves at an angle of 37 o to the original direction of motion, the other recoils at 53 o to that same axis. Find the final speeds of the two protons. v 1 v 0 = 3. 5 x 105 m/s initial 37 o 53 o v 2 final

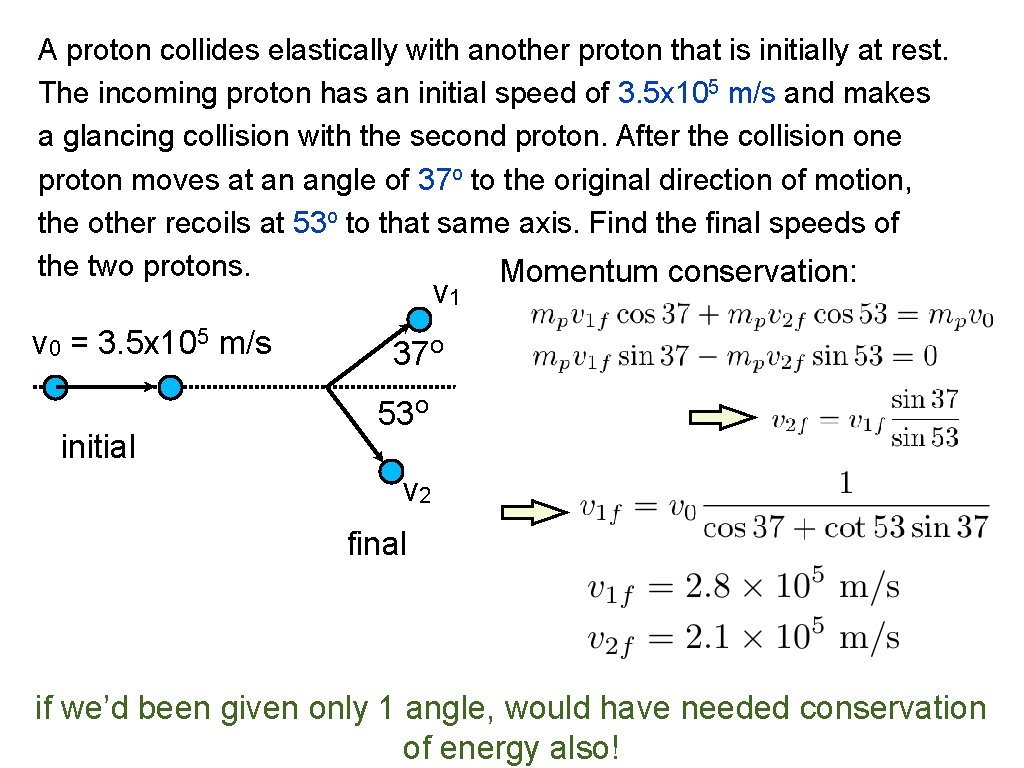
A proton collides elastically with another proton that is initially at rest. The incoming proton has an initial speed of 3. 5 x 105 m/s and makes a glancing collision with the second proton. After the collision one proton moves at an angle of 37 o to the original direction of motion, the other recoils at 53 o to that same axis. Find the final speeds of the two protons. Momentum conservation: v 1 v 0 = 3. 5 x 105 m/s initial 37 o 53 o v 2 final if we’d been given only 1 angle, would have needed conservation of energy also!

Rotational Kinematics

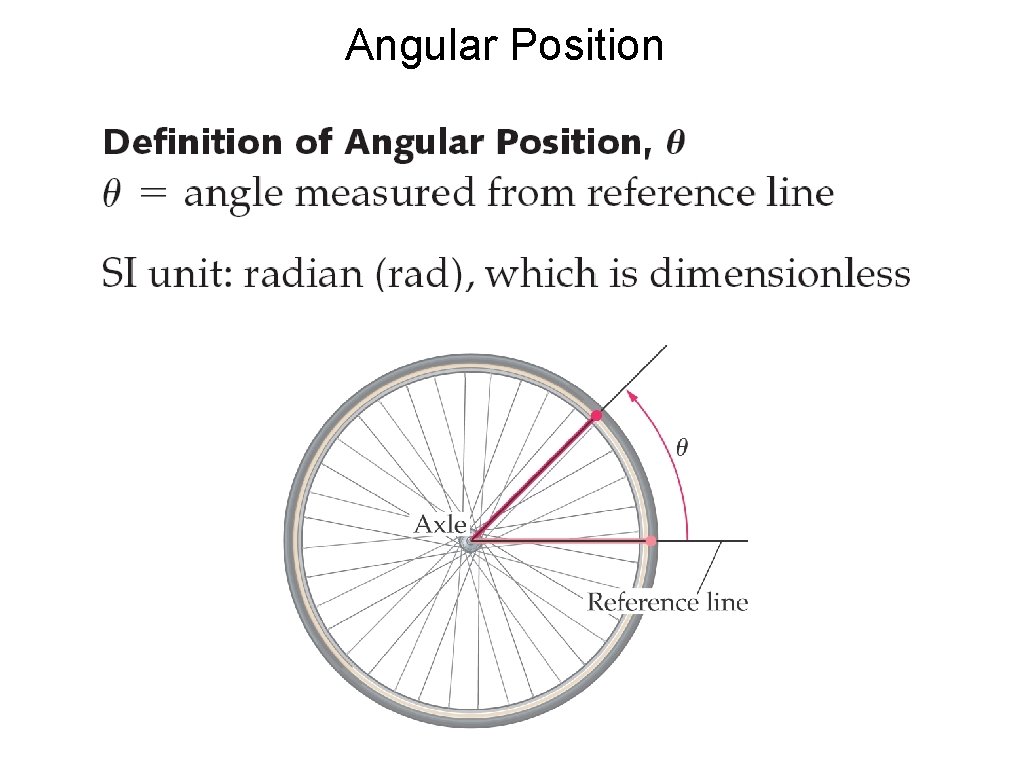
Angular Position

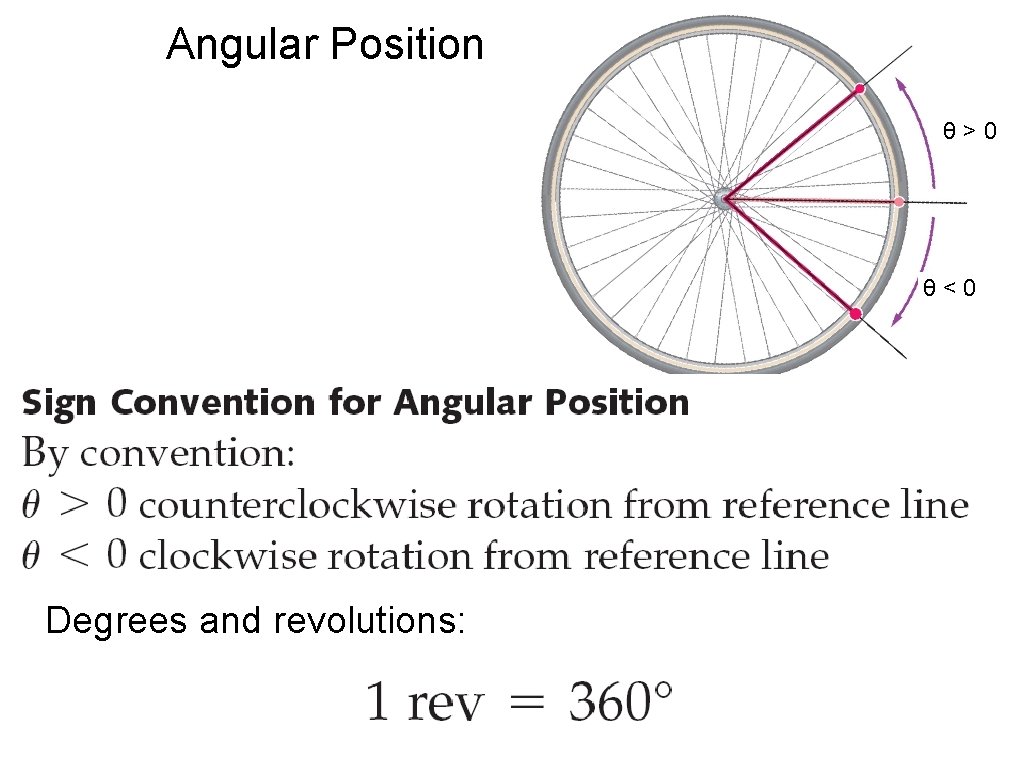
Angular Position θ>0 θ<0 Degrees and revolutions:

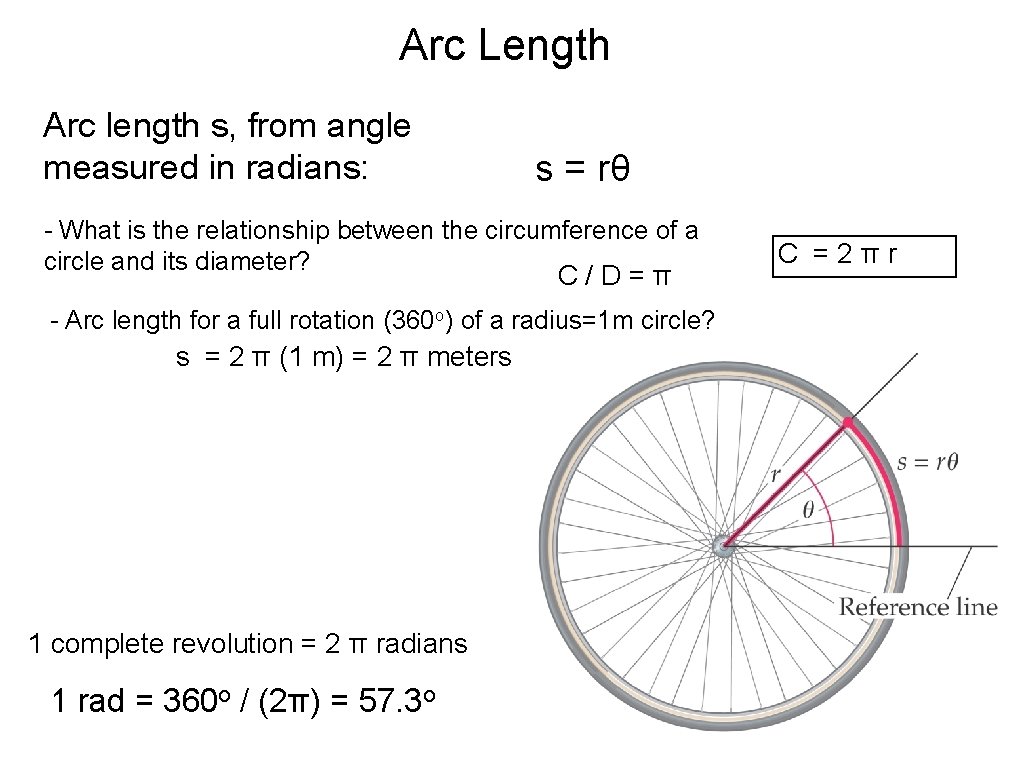
Arc Length Arc length s, from angle measured in radians: s = rθ - What is the relationship between the circumference of a circle and its diameter? C/D=π - Arc length for a full rotation (360 o) of a radius=1 m circle? s = 2 π (1 m) = 2 π meters 1 complete revolution = 2 π radians 1 rad = 360 o / (2π) = 57. 3 o C =2πr

Angular Velocity

Instantaneous Angular Velocity Period = How long it takes to go 1 full revolution Period T: SI unit: second, s

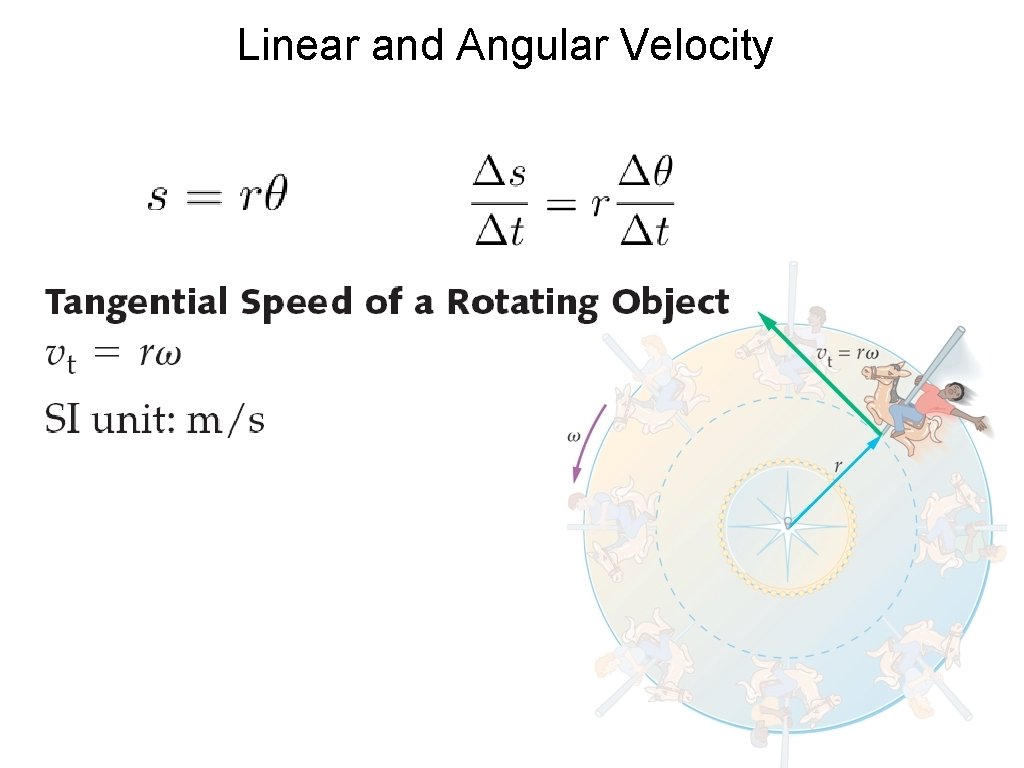
Linear and Angular Velocity

Greater translation for same rotation

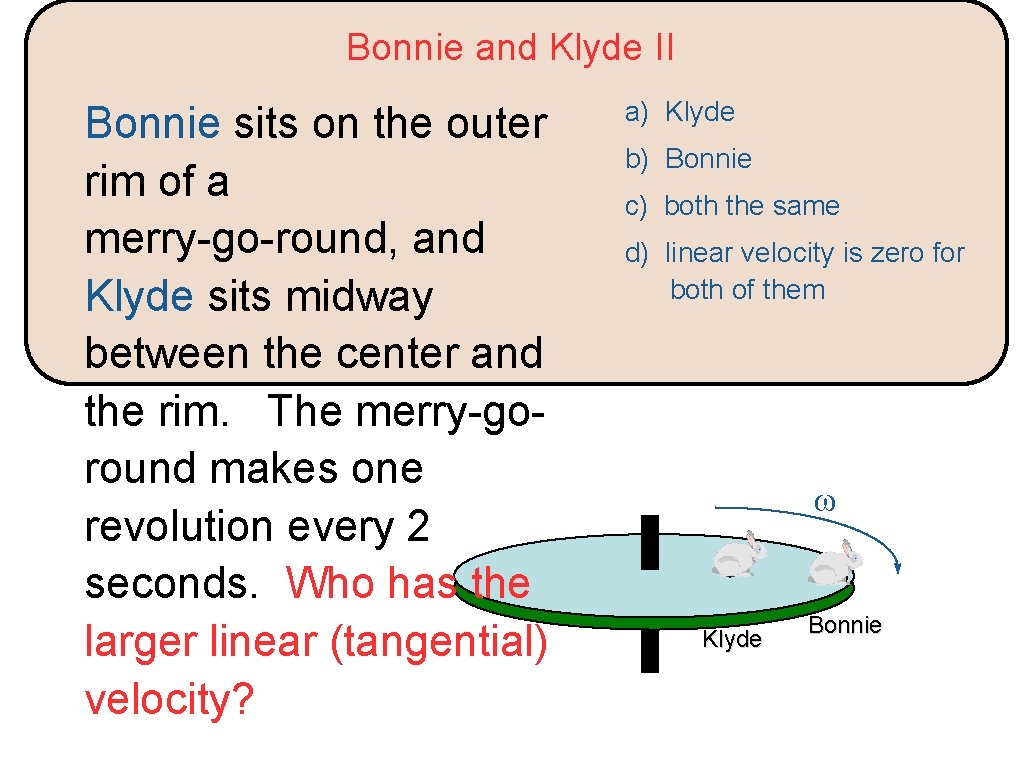
Bonnie and Klyde II Bonnie sits on the outer rim of a merry-go-round, and Klyde sits midway between the center and the rim. The merry-goround makes one revolution every 2 seconds. Who has the larger linear (tangential) velocity? a) Klyde b) Bonnie c) both the same d) linear velocity is zero for both of them ω Klyde Bonnie

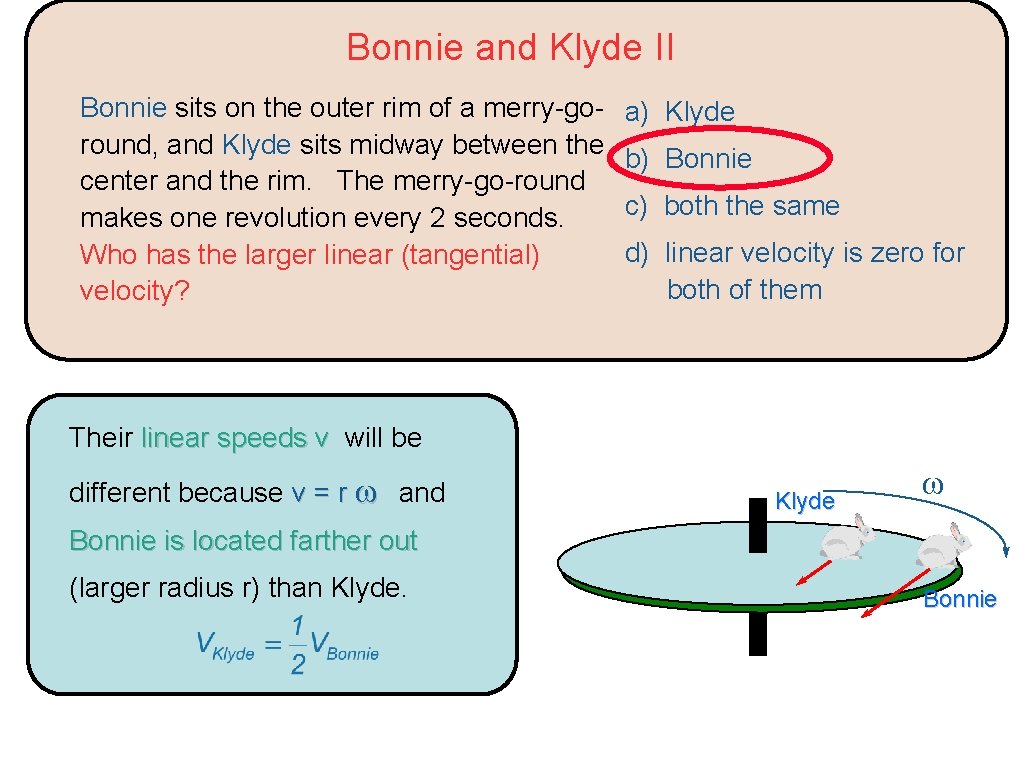
Bonnie and Klyde II Bonnie sits on the outer rim of a merry-goround, and Klyde sits midway between the center and the rim. The merry-go-round makes one revolution every 2 seconds. Who has the larger linear (tangential) velocity? a) Klyde b) Bonnie c) both the same d) linear velocity is zero for both of them Their linear speeds v will be different because v = r ω and Klyde ω Bonnie is located farther out (larger radius r) than Klyde. Bonnie

Angular Acceleration

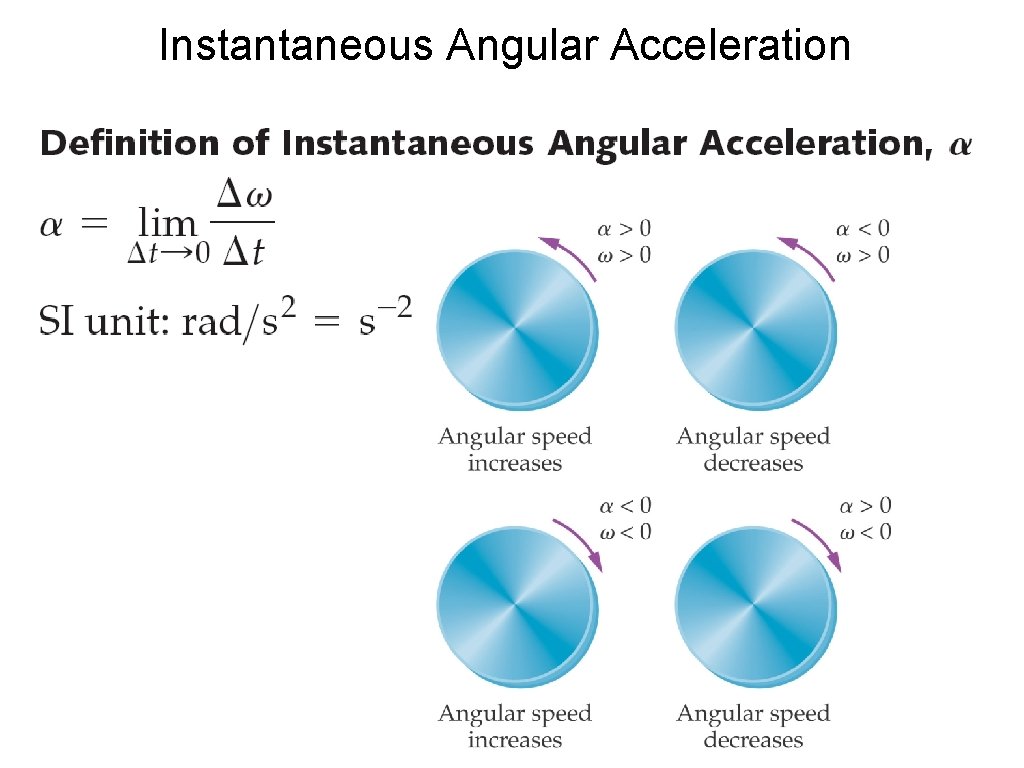
Instantaneous Angular Acceleration

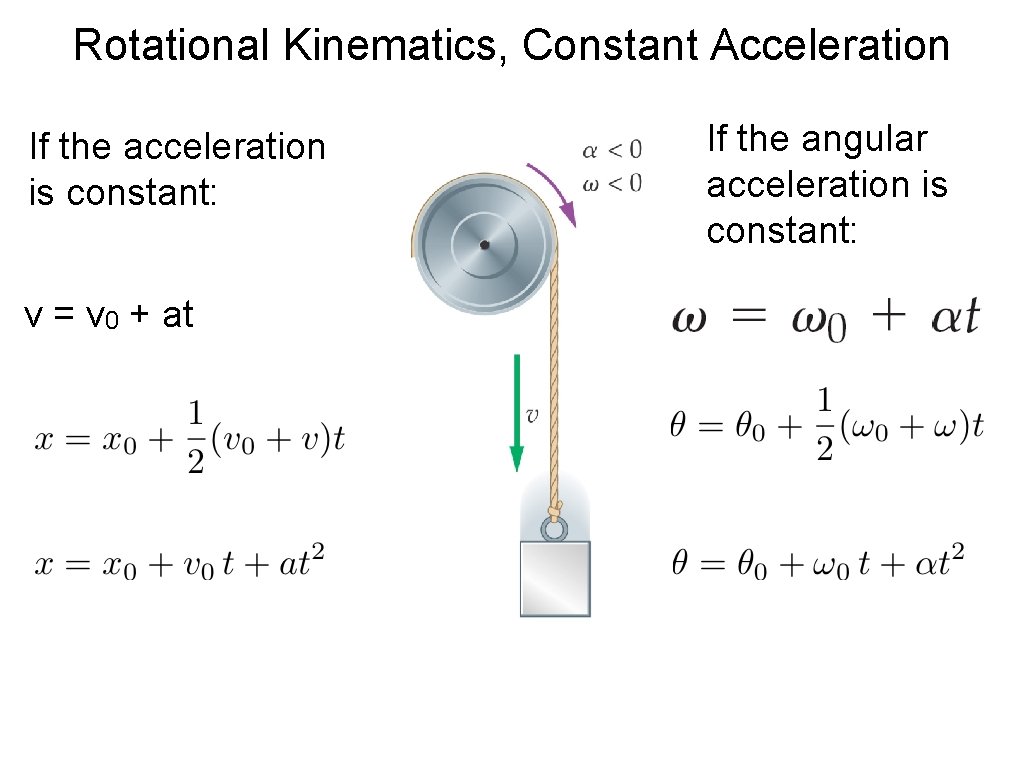
Rotational Kinematics, Constant Acceleration If the acceleration is constant: v = v 0 + at If the angular acceleration is constant:

Analogies between linear and rotational kinematics:

Angular Displacement I a) ½ θ An object at rest begins to rotate with a constant angular acceleration. If this object rotates through an angle θ in the time t, through what angle did it rotate in the time t? ½ b) ¼ θ c) ¾ θ d) 2 θ e) 4 θ

Angular Displacement I a) ½ θ An object at rest begins to rotate with a constant angular acceleration. If this object rotates through an angle θ in the time t, through what angle did it rotate in the time t½ ? The angular displacement is θ = b) ¼ θ c) ¾ θ d) 2 θ e) 4 θ αt 2 (starting from rest), and there is a quadratic dependence on time. Therefore, in half the time, time the object has rotated through one-quarter the angle

Which child experiences a greater acceleration? (assume constant angular speed)

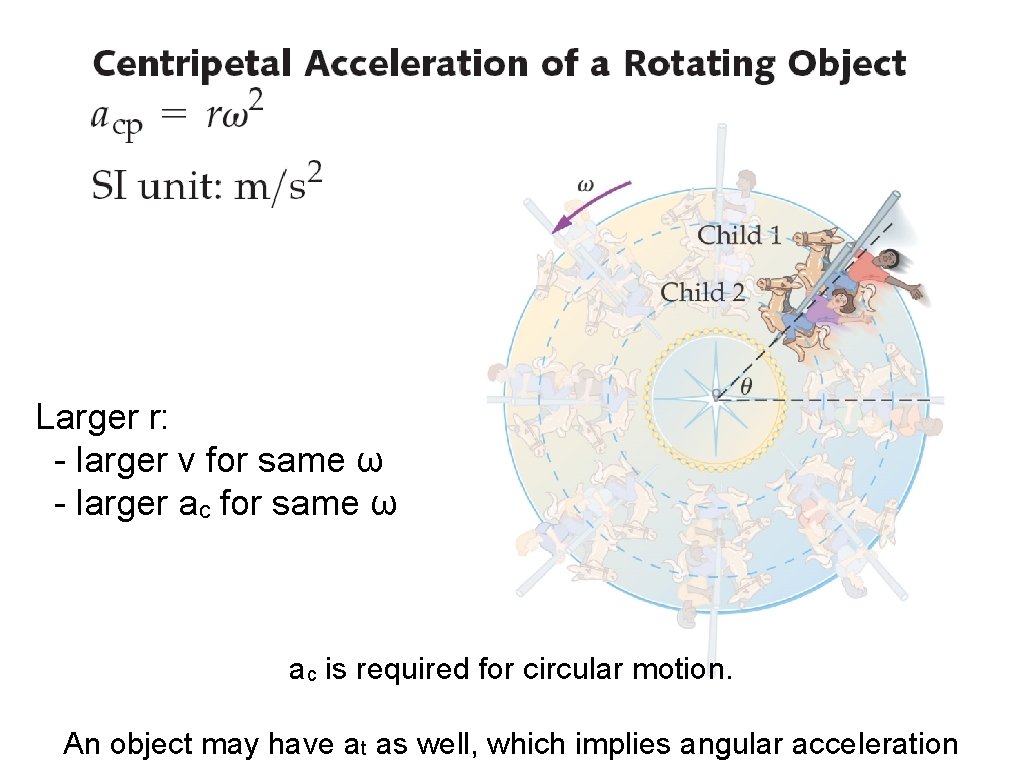
Larger r: - larger v for same ω - larger ac for same ω ac is required for circular motion. An object may have at as well, which implies angular acceleration

Angular acceleration and total linear acceleration