LargeScale Phylogenetic Analysis Tandy Warnow Associate Professor Department








![DCM-Boosting [Warnow et al. 2001] • DCM+SQS is a two-phase procedure which reduces the DCM-Boosting [Warnow et al. 2001] • DCM+SQS is a two-phase procedure which reduces the](https://slidetodoc.com/presentation_image_h/05f4a22a6a04639d2c66ed8631502722/image-16.jpg)









![GRAPPA [Bader et al. , PSB’ 01] (Genome Rearrangements Analysis under Parsimony and other GRAPPA [Bader et al. , PSB’ 01] (Genome Rearrangements Analysis under Parsimony and other](https://slidetodoc.com/presentation_image_h/05f4a22a6a04639d2c66ed8631502722/image-40.jpg)





- Slides: 46

Large-Scale Phylogenetic Analysis Tandy Warnow Associate Professor Department of Computer Sciences Graduate Program in Evolution and Ecology Co-Director The Center for Computational Biology and Bioinformatics The University of Texas at Austin

Outline of Talk • Phylogenetic reconstruction from DNA sequences – the problems, and the progress • Phylogenetic reconstruction from gene order and content in whole genomes – initial work • The future of large-scale phylogeny, and the possibilities of inferring the “Tree of Life”

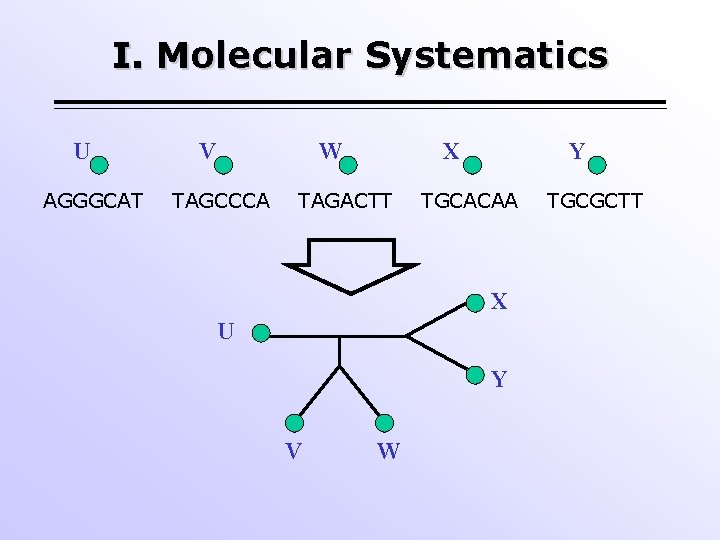
I. Molecular Systematics U AGGGCAT V W TAGCCCA X TAGACTT Y TGCACAA X U Y V W TGCGCTT

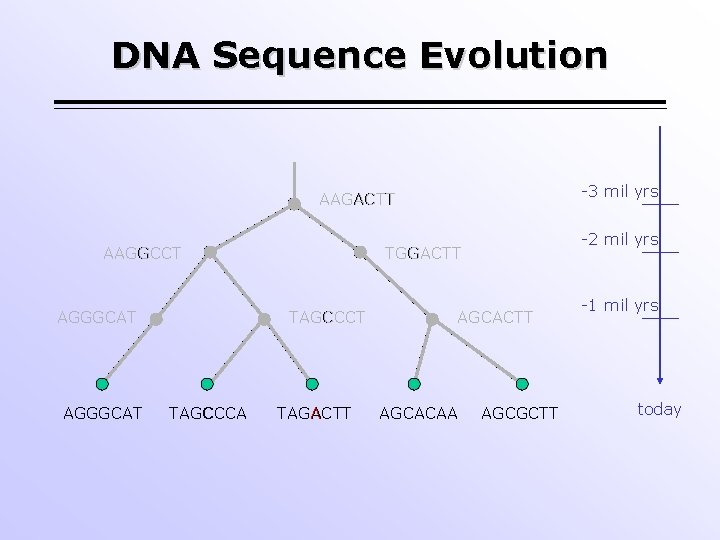
DNA Sequence Evolution -3 mil yrs AAGACTT AAGGCCT AGGGCAT TAGCCCA -2 mil yrs TGGACTT TAGACTT AGCACAA AGCGCTT -1 mil yrs today

Major Phylogenetic Reconstruction Methods • Polynomial-time distance-based methods (neighbor joining the most popular) • NP-hard sequence-based methods – Maximum Parsimony – Maximum Likelihood • Heated debates over the relative performance of these methods

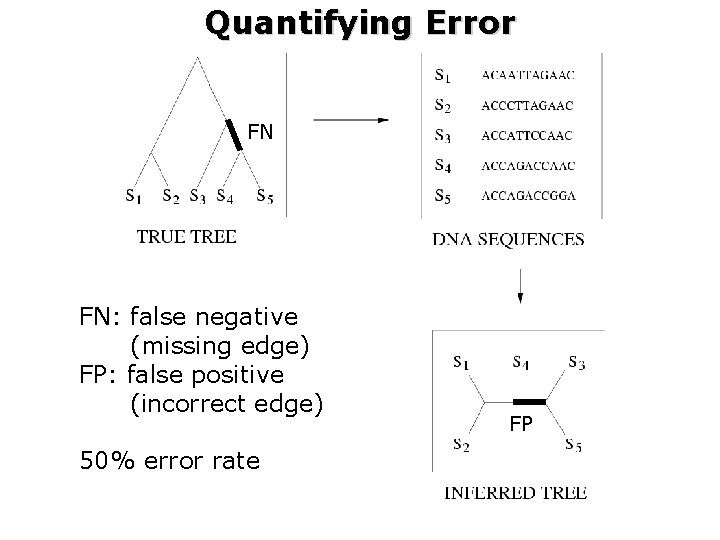
Quantifying Error FN FN: false negative (missing edge) FP: false positive (incorrect edge) 50% error rate FP

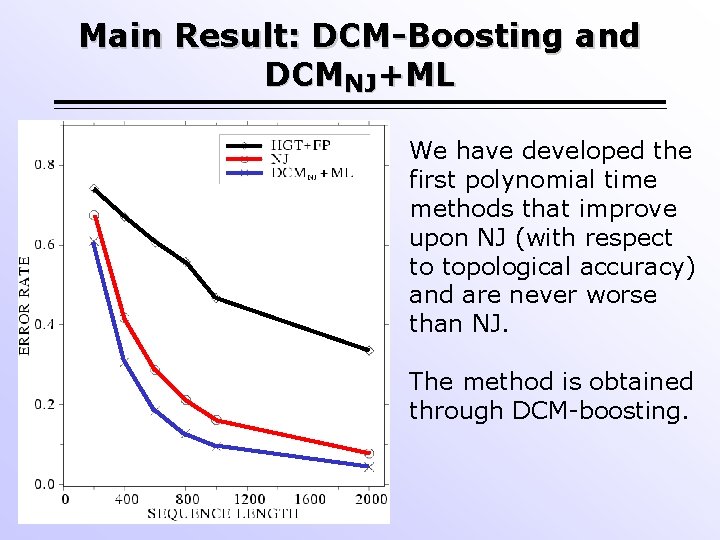
Main Result: DCM-Boosting and DCMNJ+ML We have developed the first polynomial time methods that improve upon NJ (with respect to topological accuracy) and are never worse than NJ. The method is obtained through DCM-boosting.

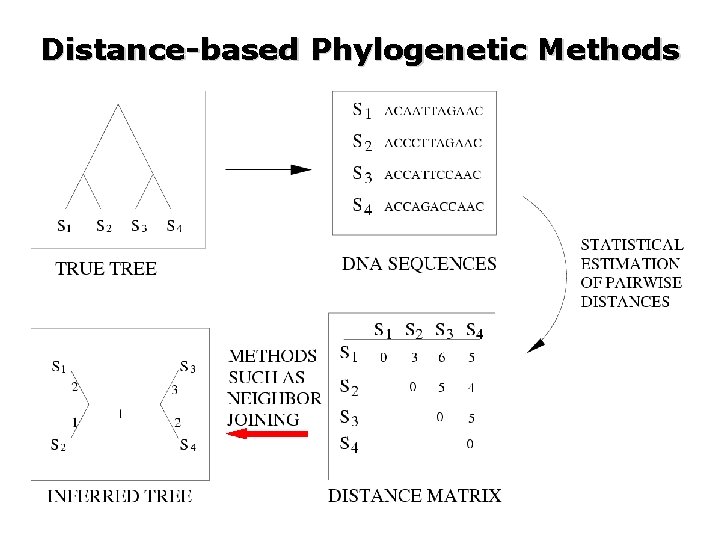
Basis of Distance-Based Methods: Additivity • A distance matrix tree and. is additive if there exists a such that • Waterman et al. (1977) showed that:

Distance-based Phylogenetic Methods

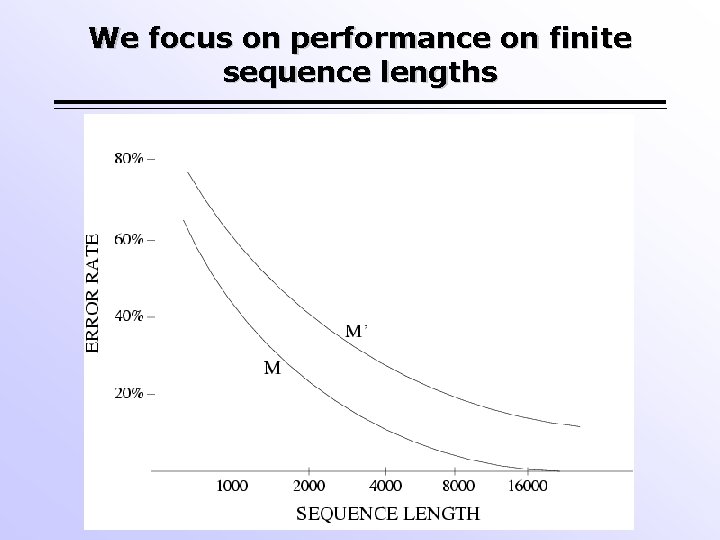
Statistical Consistency Atteson (1990) showed that is small enough. if Sequence length Hence NJ is statistically consistent for many models of evolution. But what about performance on finite sequence lengths?

We focus on performance on finite sequence lengths

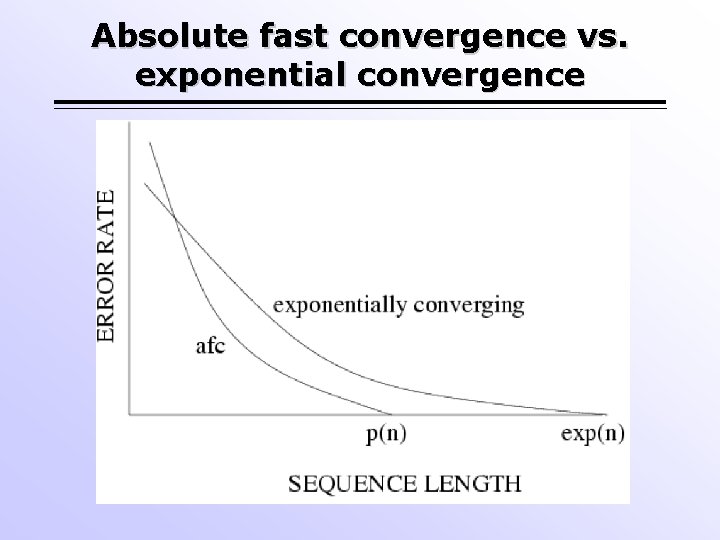
Absolute fast convergence vs. exponential convergence

General Markov (GM) Model • A GM model tree is a pair – – where is a rooted binary tree. , and is a stochastic substitution matrix with. – The sequence at the root of is drawn from a uniform distribution. – the rates of evolution across the sites can be drawn from a fixed distribution • GM contains models like Jukes-Cantor (JC) and Kimura 2 -Parameter (K 2 P) models.

Absolute Fast Convergence • Let. Define parameterize the GM model: . We • A phylogenetic reconstruction method is absolute fast-converging (AFC) for the GM model if for all positive there is a polynomial such that for all on set of sequences of length at least generated on , we have

Theoretical Comparison of Early AFC Methods to NJ • Theorem 1 [Warnow et al. 2001] DCMNJ+SQS is absolute fast converging for the GM model. • Theorem 2 [Csűrös 2001] HGT+FP is absolute fast converging for the GM model. • Theorem 3 [Atteson 1999] NJ is exponentially converging for the GM model (but is not known to be AFC).
![DCMBoosting Warnow et al 2001 DCMSQS is a twophase procedure which reduces the DCM-Boosting [Warnow et al. 2001] • DCM+SQS is a two-phase procedure which reduces the](https://slidetodoc.com/presentation_image_h/05f4a22a6a04639d2c66ed8631502722/image-16.jpg)
DCM-Boosting [Warnow et al. 2001] • DCM+SQS is a two-phase procedure which reduces the sequence length requirement of methods. Exponentially converging method DCM SQS Absolute fast converging method • DCMNJ+SQS is the result of DCM-boosting NJ.

Experimental Comparison of Early AFC Methods to NJ • rbc. L 500 -taxon tree • Jukes-Cantor model • Avg. branch length = 0. 264

Improving upon early AFC methods • These early AFC methods outperform NJ only on long enough sequences and on large enough trees with high enough rates of evolution. • Hence we need new fast converging methods which improve upon NJ on more of the parameter space, and are never worse than NJ. • We modify the second phase to improve the empirical performance, replacing SQS with ML (maximum likelihood) or MP (maximum parsimony).

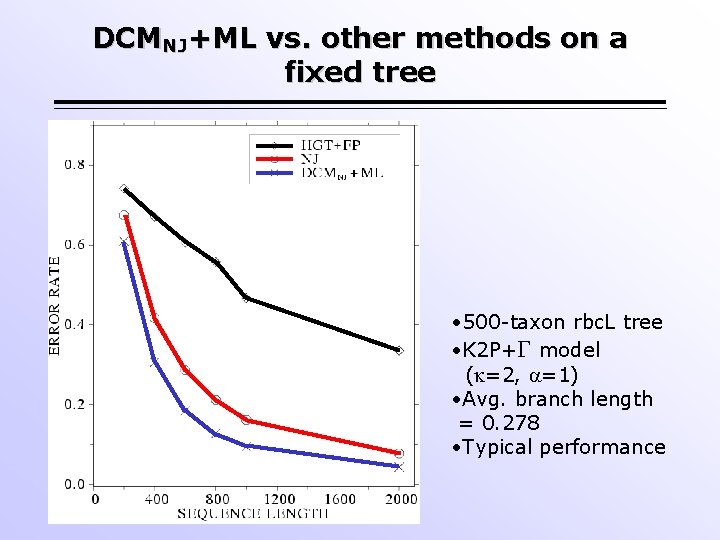
DCMNJ+ML vs. other methods on a fixed tree • 500 -taxon rbc. L tree • K 2 P+ model ( =2, =1) • Avg. branch length = 0. 278 • Typical performance

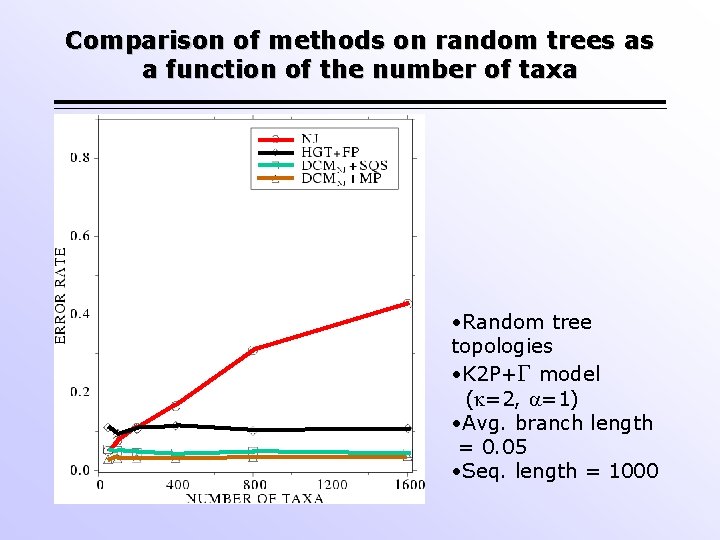
Comparison of methods on random trees as a function of the number of taxa • Random tree topologies • K 2 P+ model ( =2, =1) • Avg. branch length = 0. 05 • Seq. length = 1000

Summary • These are the first polynomial time methods that improve upon NJ (with respect to topological accuracy) and are never worse than NJ. • The advantage obtained with DCMNJ+MP and DCMNJ+ML increases with number of taxa. • In practice these new methods are slower than NJ (minutes vs. seconds), but still much faster than MP and ML (which can take days). • Conjecture: DCMNJ+ML is AFC.

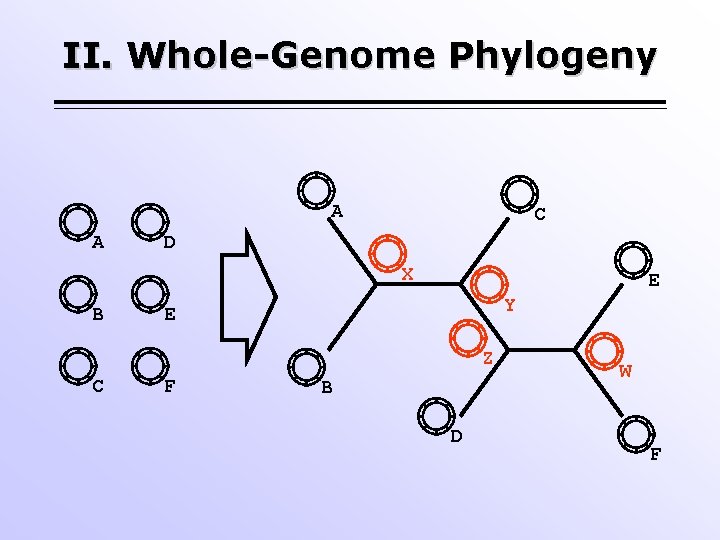
II. Whole-Genome Phylogeny A A C D X B E Y E Z C F B D W F

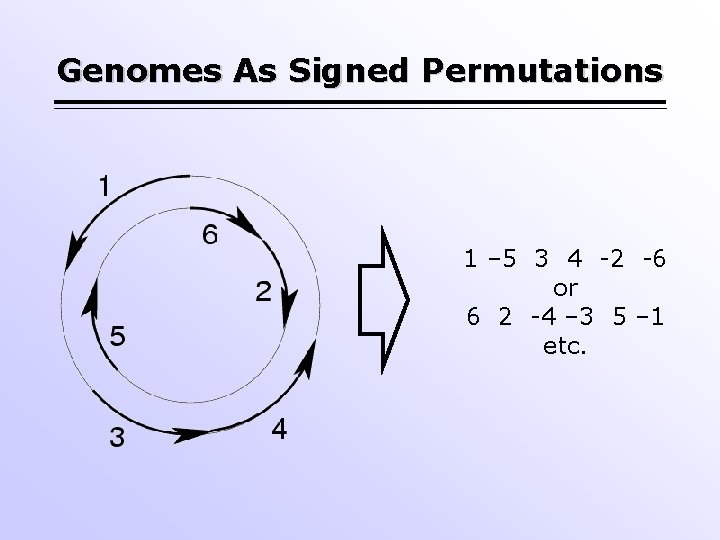
Genomes As Signed Permutations 1 – 5 3 4 -2 -6 or 6 2 -4 – 3 5 – 1 etc.

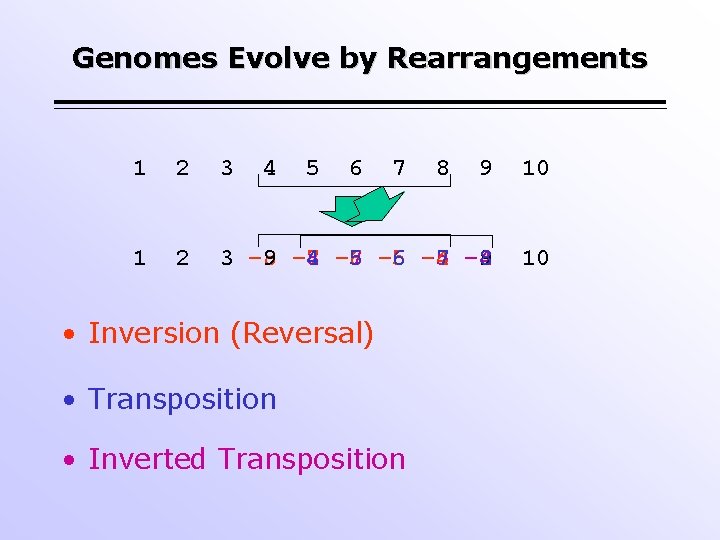
Genomes Evolve by Rearrangements 1 2 3 4 5 6 7 9 10 1 2 3 – 8 9 – 7 -8 4 – 6 – 7 5 – 6 6 -4 – 5 7 – 4 8 9 10 • Inversion (Reversal) • Transposition • Inverted Transposition 8

Genome Rearrangement Has A Huge State Space • DNA sequences : 4 states per site • Signed circular genomes with n genes: states, 1 site • Circular genomes (1 site) – with 37 genes: states – with 120 genes: states

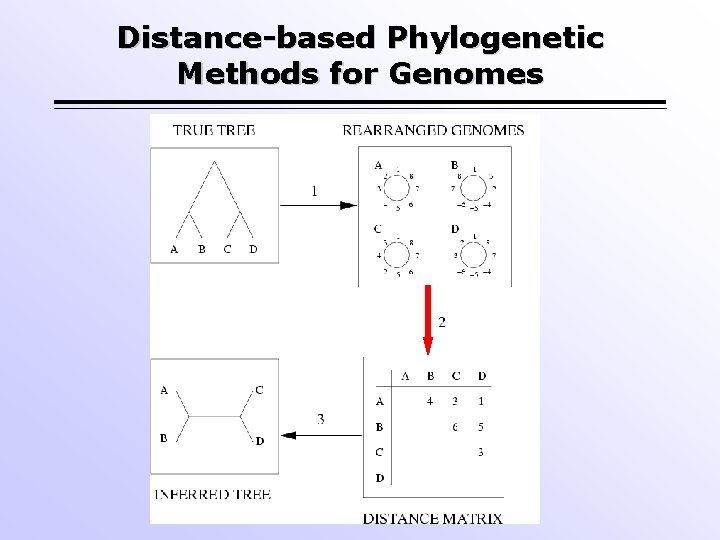
Distance-based Phylogenetic Methods for Genomes

Genomic Distance Estimators • Standard: – Breakpoint distance – (Minimum) Inversion distance • Our estimators: We attempt to estimate the actual number of events (the ``true evolutionary distance”): – EDE [Moret et al, ISMB’ 01] – Approx-IEBP [Wang and Warnow, STOC’ 01] – Exact-IEBP [Wang, WABI’ 01]

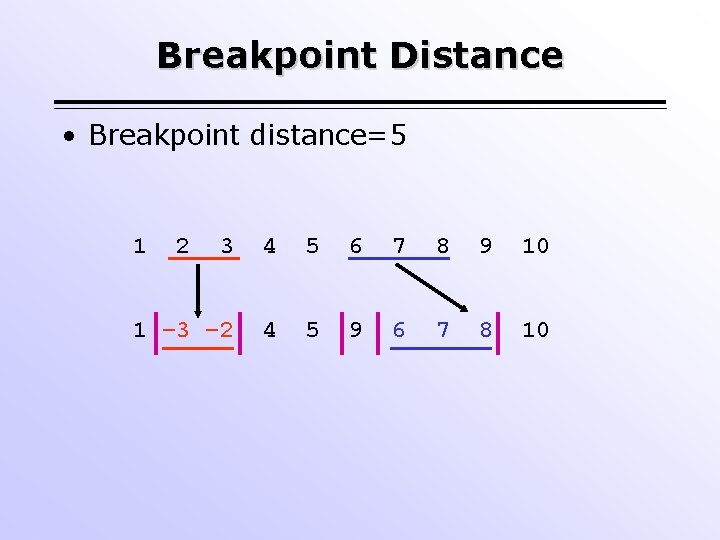
Breakpoint Distance • Breakpoint distance=5 1 2 3 4 5 6 7 8 9 10 1 – 3 – 2 4 5 9 6 7 8 10

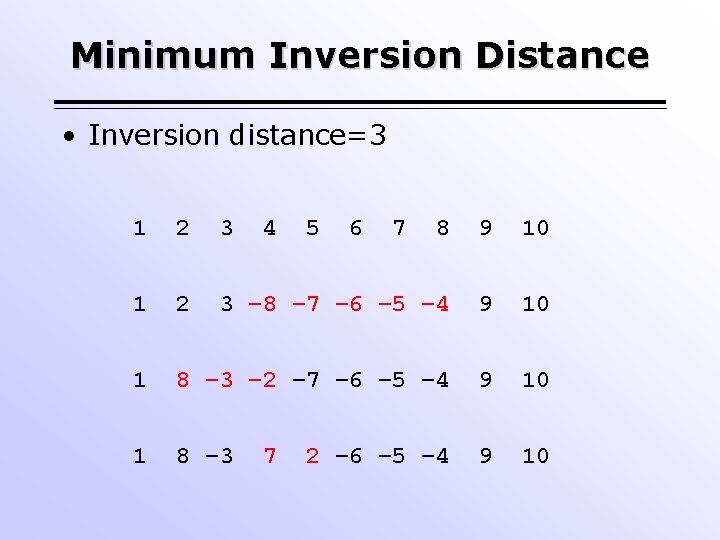
Minimum Inversion Distance • Inversion distance=3 1 2 3 4 8 9 10 1 2 3 – 8 – 7 – 6 – 5 – 4 9 10 1 8 – 3 – 2 – 7 – 6 – 5 – 4 9 10 1 8 – 3 9 10 7 5 6 7 2 – 6 – 5 – 4

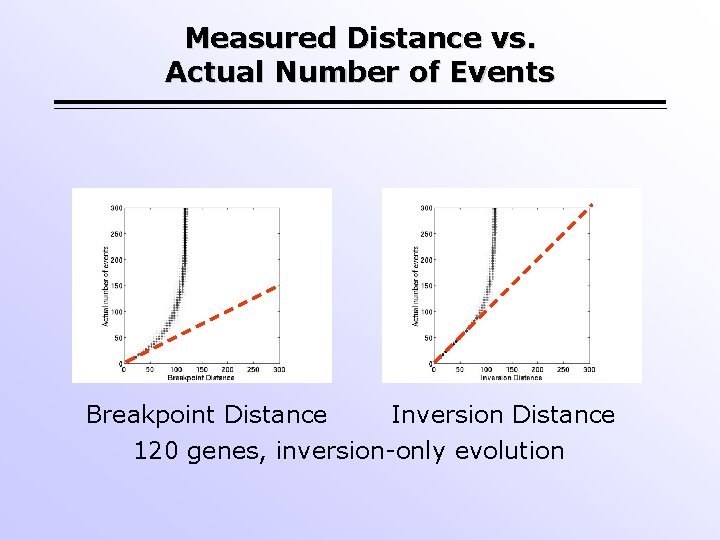
Measured Distance vs. Actual Number of Events Breakpoint Distance Inversion Distance 120 genes, inversion-only evolution

Generalized Nadeau-Taylor Model • Three types of events: – Inversions – Transpositions – Inverted Transpositions • Events of the same type are equiprobable • Probability of the three types have fixed ratio: Inv : Trp : Inv. Trp = (1 -a-b): a: b

Estimating True Evolutionary Distances for Genomes Given fixed probabilities for each type of event, we estimate the expected breakpoint distance after k random events: • Approx-IEBP [Wang, Warnow 2001] – Polynomial-time closed-form approximation to the expected breakpoint distance – Proven error bound • Exact-IEBP [Wang 2001] – Exact, recursive solution for the expected breakpoint distance – Polynomial-time but slower than Approx-IEBP

Estimating True Evolutionary Distances for Genomes (cont. ) Estimating the expected Inversion distance: EDE [Moret, Wang, Warnow, Wyman 2001] – Closed-formula based upon an empirical estimation of the expected inversion distance after k random events (based upon 120 genes and inversion only, but robust to errors in the model). – Polynomial time, fastest of the three.

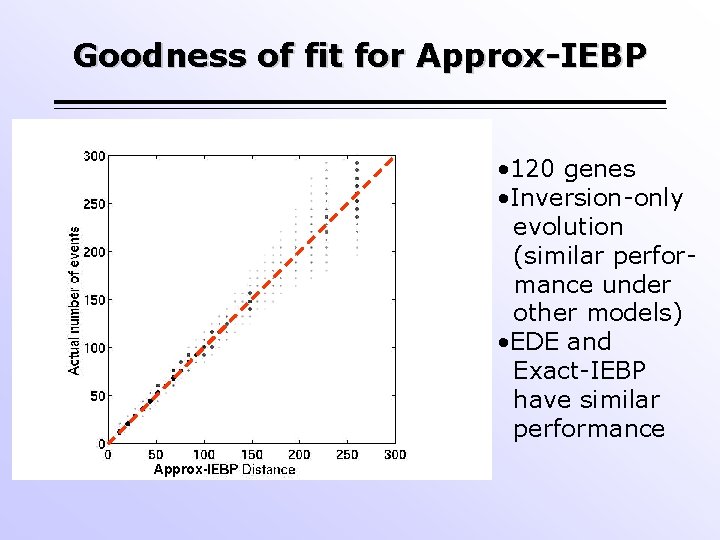
Goodness of fit for Approx-IEBP • 120 genes • Inversion-only evolution (similar performance under other models) • EDE and Exact-IEBP have similar performance Approx-

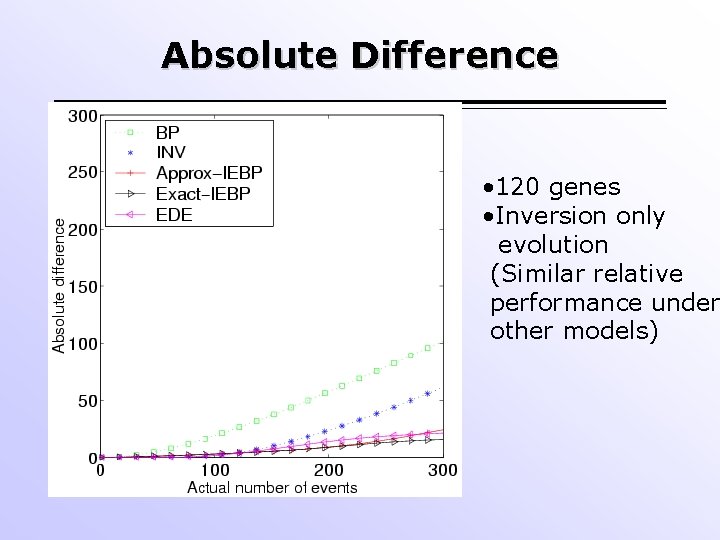
Absolute Difference • 120 genes • Inversion only evolution (Similar relative performance under other models)

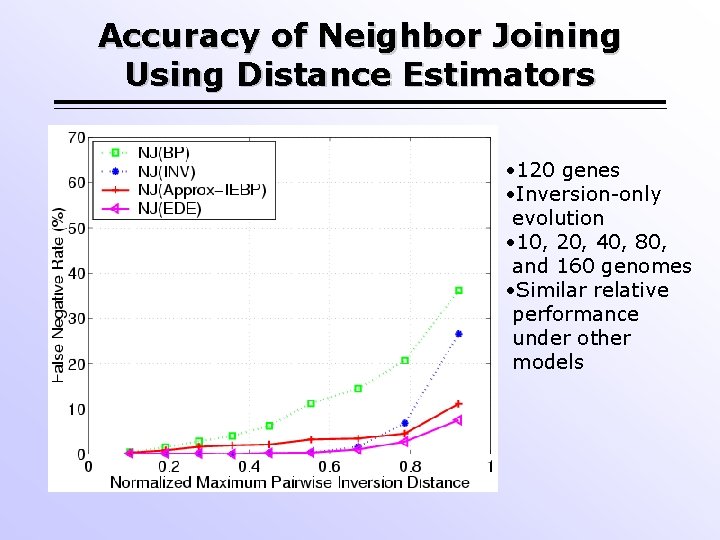
Accuracy of Neighbor Joining Using Distance Estimators • 120 genes • Inversion-only evolution • 10, 20, 40, 80, and 160 genomes • Similar relative performance under other models

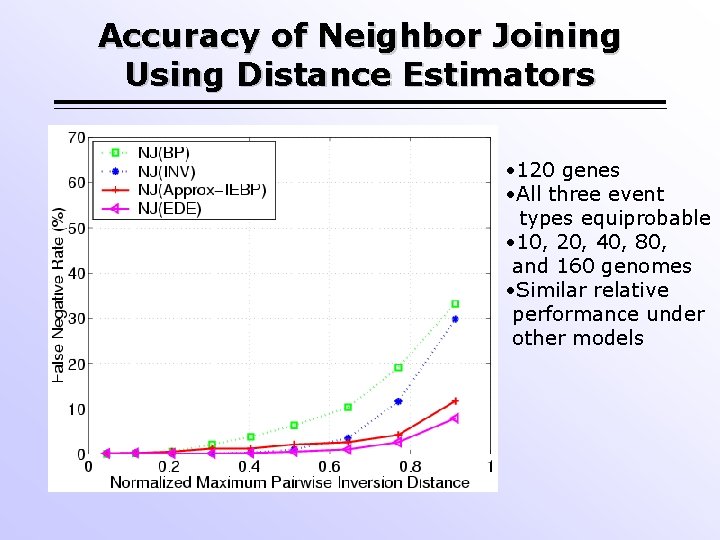
Accuracy of Neighbor Joining Using Distance Estimators • 120 genes • All three event types equiprobable • 10, 20, 40, 80, and 160 genomes • Similar relative performance under other models

Summary of Genomic Distance Estimators • Statistically based estimation of genomic distances improves NJ analyses • Our IEBP estimators assume knowledge of the probabilities of each type of event, but are robust to model violations • NJ(EDE) outperforms NJ on other estimators, under all models studied • Accuracy is very good, except when very close to saturation

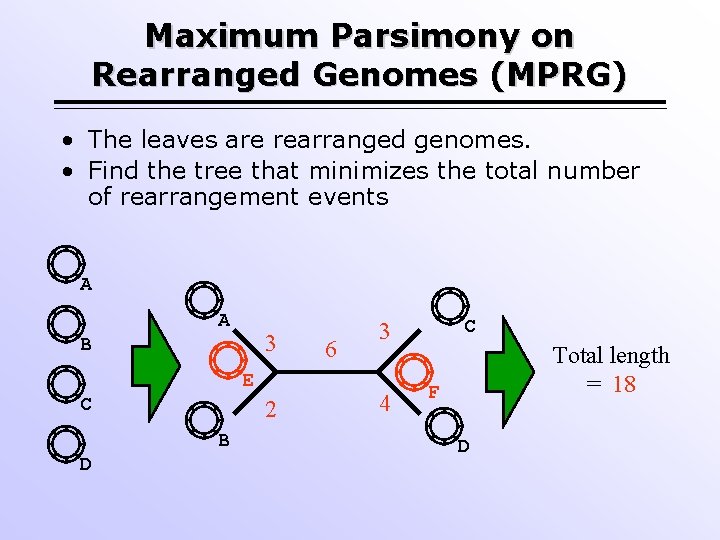
Maximum Parsimony on Rearranged Genomes (MPRG) • The leaves are rearranged genomes. • Find the tree that minimizes the total number of rearrangement events A A 3 B E C 2 B D 6 C 3 4 Total length = 18 F D
![GRAPPA Bader et al PSB 01 Genome Rearrangements Analysis under Parsimony and other GRAPPA [Bader et al. , PSB’ 01] (Genome Rearrangements Analysis under Parsimony and other](https://slidetodoc.com/presentation_image_h/05f4a22a6a04639d2c66ed8631502722/image-40.jpg)
GRAPPA [Bader et al. , PSB’ 01] (Genome Rearrangements Analysis under Parsimony and other Phylogenetic Algorithms) Reimplementation of BPAnalysis [Blanchette et al. 1997] for the Breakpoint Phylogeny problem. • Uses algorithm engineering to improve performance. • Improves the algorithm by reducing the number of tree length evaluations. (Evaluating the length of a fixed tree is NP-hard)

Campanulaceae

Analysis of Campanulaceae • 12 genomes + 1 outgroup (Tobacco) • 105 gene segments • BPAnalysis [Blanchette et al. 1997] over 200 years [Cosner et al. 2000] Using GRAPPA v 1. 1 on the 512 -processor Los Lobos Supercluster machine: 2 minutes = 100 million-fold speedup (200, 000 -fold speedup per processor)

Consensus of 216 MP Trees Strict Consensus of 216 trees; 6 out of 10 internal edges recovered. Trachelium Campanula Adenophora Symphandra Legousia Asyneuma Triodanus Wahlenbergia Merciera Codonopsis Cyananthus Platycodon Tobacco

Future Work • New focus on Rare Genomic Changes – New data – New models – New methods • New techniques for large scale analyses – Divide-and-conquer methods – Non-tree models – Visualization of large trees and large sets of trees

Acknowledgements • Funding: The David and Lucile Packard Foundation, The National Science Foundation, and Paul Angello • Collaborators: Robert Jansen (U. Texas) Bernard Moret, David Bader, Mi-Yan (U. New Mexico) Daniel Huson (Celera) Katherine St. John (CUNY) Linda Raubeson (Central Washington U. ) Luay Nakhleh, Usman Roshan, Jerry Sun, Li-San Wang, Stacia Wyman (Phylolab, U. Texas)

Phylolab, U. Texas Please visit us at http: //www. cs. utexas. edu/users/phylo/
 Tandy warnow
Tandy warnow Tandy warnow
Tandy warnow Tandy warnow
Tandy warnow Tandy warnow
Tandy warnow Tandy warnow
Tandy warnow Tandy warnow
Tandy warnow Tandy warnow
Tandy warnow Tandy warnow
Tandy warnow Promotion from assistant to associate professor
Promotion from assistant to associate professor Microsoft robotics developer studio tutorial
Microsoft robotics developer studio tutorial Hoaloha design group
Hoaloha design group What are nodes in a cladogram
What are nodes in a cladogram Species tree
Species tree Ingroup phylogenetic tree
Ingroup phylogenetic tree Chordate
Chordate Difference between cladogram and phylogenetic tree
Difference between cladogram and phylogenetic tree Section 18-2 modern evolutionary classification
Section 18-2 modern evolutionary classification Reading phylogenetic trees
Reading phylogenetic trees Building vocabulary: phylogenies
Building vocabulary: phylogenies Phylogenetic tree outline
Phylogenetic tree outline Biology taxonomy
Biology taxonomy How to understand phylogenetic tree
How to understand phylogenetic tree Basal taxon definition biology
Basal taxon definition biology Gradualism vs punctuated equilibrium
Gradualism vs punctuated equilibrium Scaled vs unscaled phylogenetic tree
Scaled vs unscaled phylogenetic tree Model 4 dichotomous key pogil answers
Model 4 dichotomous key pogil answers Cladogram kingdoms
Cladogram kingdoms Ap biology phylogenetic tree
Ap biology phylogenetic tree Extant species phylogenetic tree
Extant species phylogenetic tree Monophyletic vs polyphyletic vs paraphyletic
Monophyletic vs polyphyletic vs paraphyletic Phylogenetic tree grade 11
Phylogenetic tree grade 11 Chegg
Chegg Distabc
Distabc Urochordata characteristics
Urochordata characteristics Phylogenetic tree of animal phyla
Phylogenetic tree of animal phyla Dichotomous key template
Dichotomous key template Dear king phillip came over for good spaghetti
Dear king phillip came over for good spaghetti King phillip came over for good soup
King phillip came over for good soup Domain bacteria classification
Domain bacteria classification How to read a cladogram tree
How to read a cladogram tree Evolutionary tree of primates
Evolutionary tree of primates Phylogram vs cladogram
Phylogram vs cladogram Artiodactyla phylogeny
Artiodactyla phylogeny Mutex bullfrog
Mutex bullfrog Species tree
Species tree Phylogeny and the tree of life chapter 26
Phylogeny and the tree of life chapter 26 Chartered it professional
Chartered it professional