Phylogenetic Trees Lecture 1 Credits N Friedman D

Phylogenetic Trees Lecture 1 . Credits: N. Friedman, D. Geiger , S. Moran,

Evolution of new organisms is driven by u Diversity l Different individuals carry different variants of the same basic blue print u Mutations l The DNA sequence can be changed due to single base changes, deletion/insertion of DNA segments, etc. u Selection bias 2

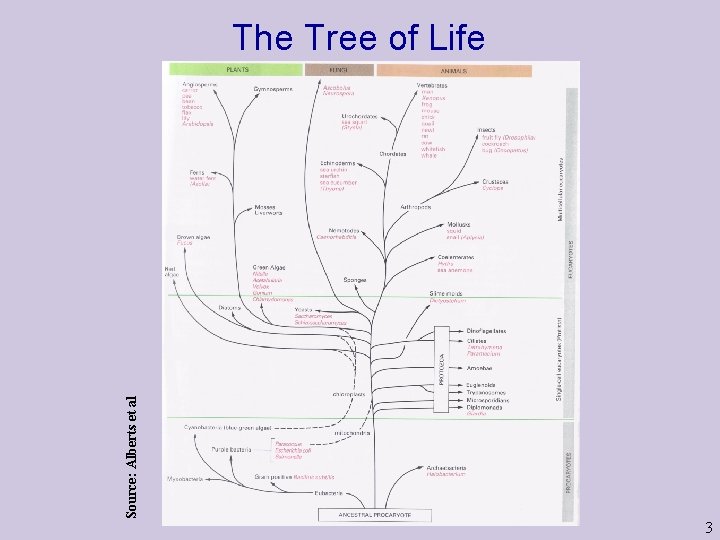
Source: Alberts et al The Tree of Life 3

Tree of life- a better picture D’après Ernst Haeckel, 1891 4

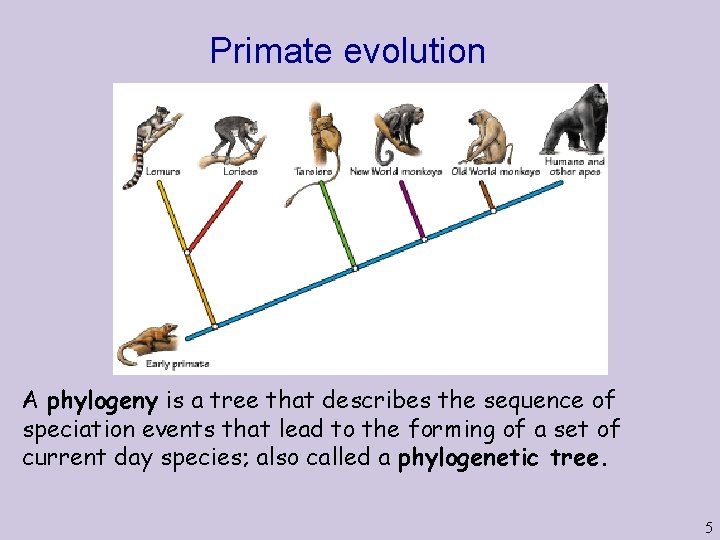
Primate evolution A phylogeny is a tree that describes the sequence of speciation events that lead to the forming of a set of current day species; also called a phylogenetic tree. 5

Historical Note u Until mid 1950’s phylogenies were constructed by experts based on their opinion (subjective criteria) u Since then, focus on objective criteria for constructing phylogenetic trees l Thousands of articles in the last decades u Important l l for many aspects of biology Classification Understanding biological mechanisms 6

Morphological vs. Molecular u Classical phylogenetic analysis: morphological features: number of legs, lengths of legs, etc. u Modern biological methods allow to use molecular features l Gene sequences l Protein sequences u Analysis based on homologous sequences (e. g. , globins) in different species 7

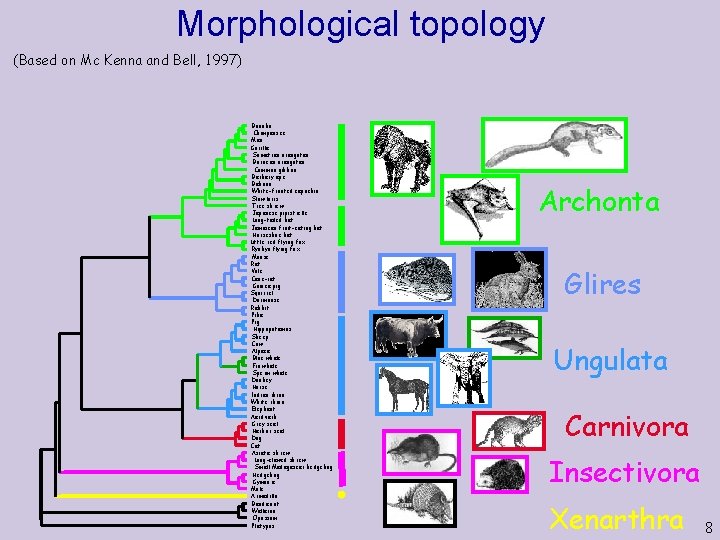
Morphological topology (Based on Mc Kenna and Bell, 1997) Bonobo Chimpanzee Man Gorilla Sumatran orangutan Bornean orangutan Common gibbon Barbary ape Baboon White-fronted capuchin Slow loris Tree shrew Japanese pipistrelle Long-tailed bat Jamaican fruit-eating bat Horseshoe bat Little red flying fox Ryukyu flying fox Mouse Rat Vole Cane-rat Guinea pig Squirrel Dormouse Rabbit Pika Pig Hippopotamus Sheep Cow Alpaca Blue whale Fin whale Sperm whale Donkey Horse Indian rhino White rhino Elephant Aardvark Grey seal Harbor seal Dog Cat Asiatic shrew Long-clawed shrew Small Madagascar hedgehog Hedgehog Gymnure Mole Armadillo Bandicoot Wallaroo Opossum Platypus Archonta Glires Ungulata Carnivora Insectivora Xenarthra 8

From sequences to a phylogenetic tree Rat QEPGGLVVPPTDA Rabbit QEPGGMVVPPTDA Gorilla QEPGGLVVPPTDA Cat REPGGLVVPPTEG There are many possible types of sequences to use (e. g. Mitochondrial vs Nuclear proteins). 9

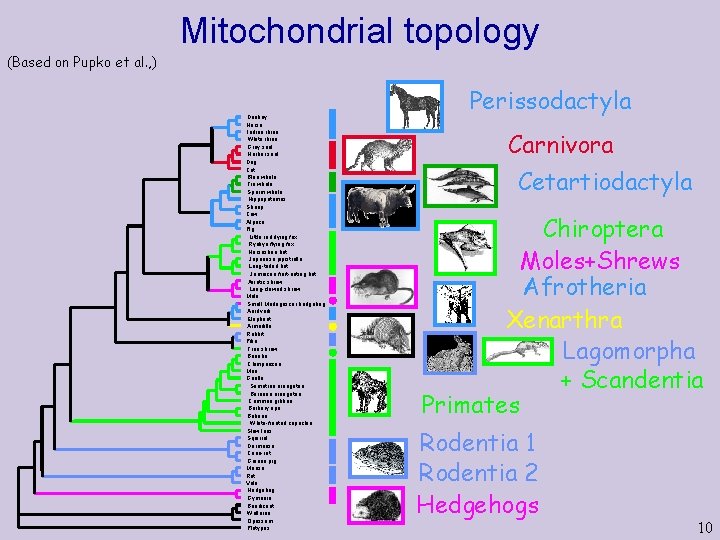
Mitochondrial topology (Based on Pupko et al. , ) Donkey Horse Indian rhino White rhino Grey seal Harbor seal Dog Cat Blue whale Fin whale Sperm whale Hippopotamus Sheep Cow Alpaca Pig Little red flying fox Ryukyu flying fox Horseshoe bat Japanese pipistrelle Long-tailed bat Jamaican fruit-eating bat Asiatic shrew Long-clawed shrew Mole Small Madagascar hedgehog Aardvark Elephant Armadillo Rabbit Pika Tree shrew Bonobo Chimpanzee Man Gorilla Sumatran orangutan Bornean orangutan Common gibbon Barbary ape Baboon White-fronted capuchin Slow loris Squirrel Dormouse Cane-rat Guinea pig Mouse Rat Vole Hedgehog Gymnure Bandicoot Wallaroo Opossum Platypus Perissodactyla Carnivora Cetartiodactyla Chiroptera Moles+Shrews Afrotheria Xenarthra Lagomorpha + Scandentia Primates Rodentia 1 Rodentia 2 Hedgehogs 10

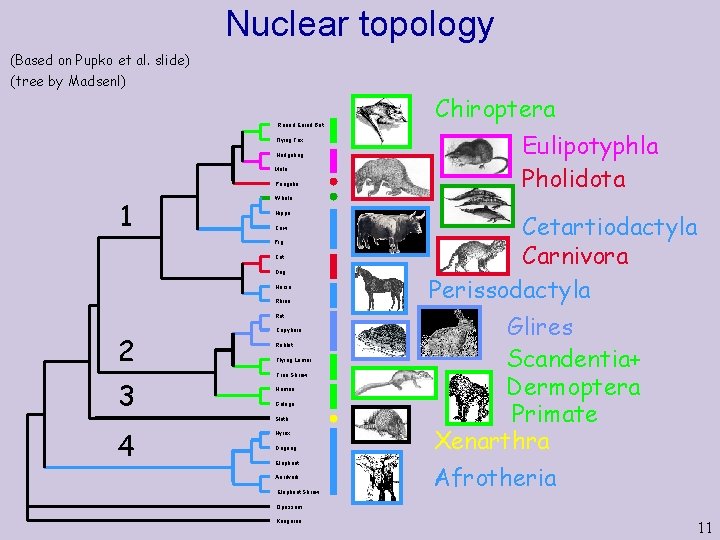
Nuclear topology (Based on Pupko et al. slide) (tree by Madsenl) Round Eared Bat Flying Fox Hedgehog Mole Pangolin 1 Cow Cat Dog Horse Rhino Rat 3 Capybara Rabbit Flying Lemur Tree Shrew Human Galago Sloth 4 Eulipotyphla Pholidota Whale Hippo Pig 2 Chiroptera Hyrax Dugong Elephant Aardvark Elephant Shrew Cetartiodactyla Carnivora Perissodactyla Glires Scandentia+ Dermoptera Primate Xenarthra Afrotheria Opossum Kangaroo 11

Theory of Evolution u Basic idea l speciation events lead to creation of different species. l Speciation caused by physical separation into groups where different genetic variants become dominant u Any two species share a (possibly distant) common ancestor 12

Basic Assumptions • Closer related organisms have more similar genomes. • Highly similar genes are homologous (have the same ancestor). • A universal ancestor exists for all life forms. • Molecular difference in homologous genes (or protein sequences) are positively correlated with evolution time. • Phylogenetic relation can be expressed by a dendrogram (a “tree”). .

Phylogenenetic trees Aardvark Bison Chimp Dog Elephant Leafs - current day species u Nodes - hypothetical most recent common ancestors u Edges length - “time” from one speciation to the next u 14

Dangers in Molecular Phylogenies u We have to emphasize that gene/protein sequence can be homologous for several different reasons: u Orthologs -- sequences diverged after a speciation event u Paralogs -- sequences diverged after a duplication event u Xenologs -- sequences diverged after a horizontal transfer (e. g. , by virus) 15

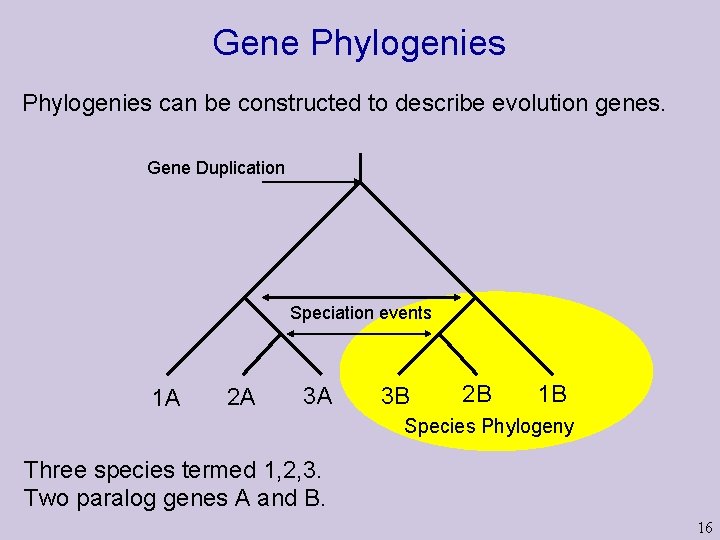
Gene Phylogenies can be constructed to describe evolution genes. Gene Duplication Speciation events 1 A 2 A 3 A 3 B 2 B 1 B Species Phylogeny Three species termed 1, 2, 3. Two paralog genes A and B. 16

Dangers of Paralogs If we happen to consider genes 1 A, 2 B, and 3 A of species 1, 2, 3, we get a wrong tree that does not represent the phylogeny of the host species of the given sequences because duplication does not create new species. S Gene Duplication S 1 A 2 A Speciation events 3 A 3 B S 2 B 1 B In the sequel we assume all given sequences are orthologs. 17

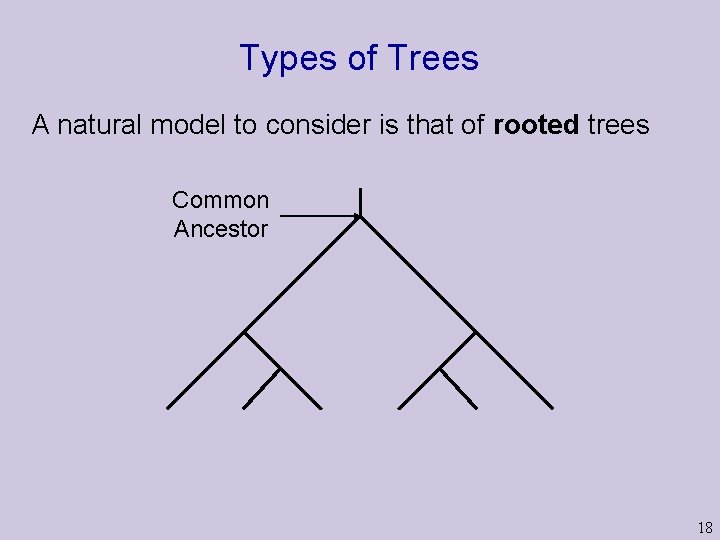
Types of Trees A natural model to consider is that of rooted trees Common Ancestor 18

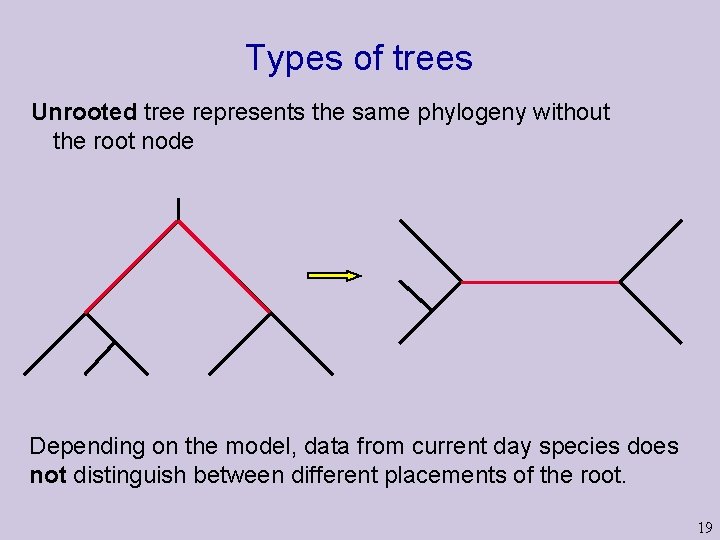
Types of trees Unrooted tree represents the same phylogeny without the root node Depending on the model, data from current day species does not distinguish between different placements of the root. 19

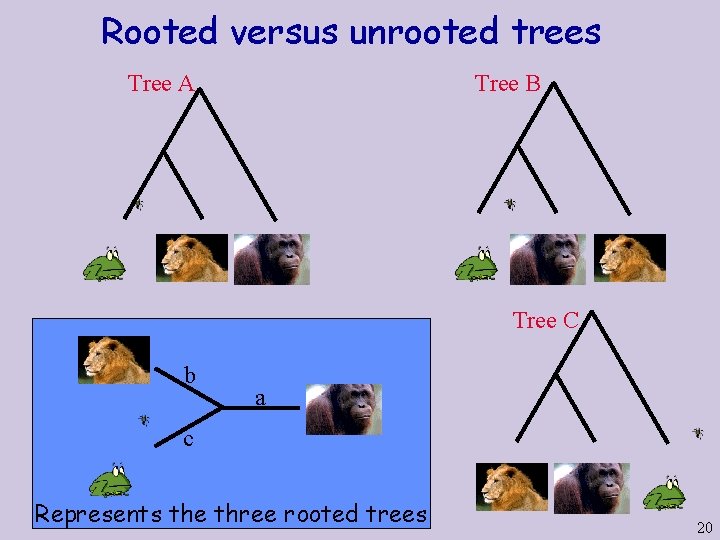
Rooted versus unrooted trees Tree A Tree B Tree C b a c Represents the three rooted trees 20

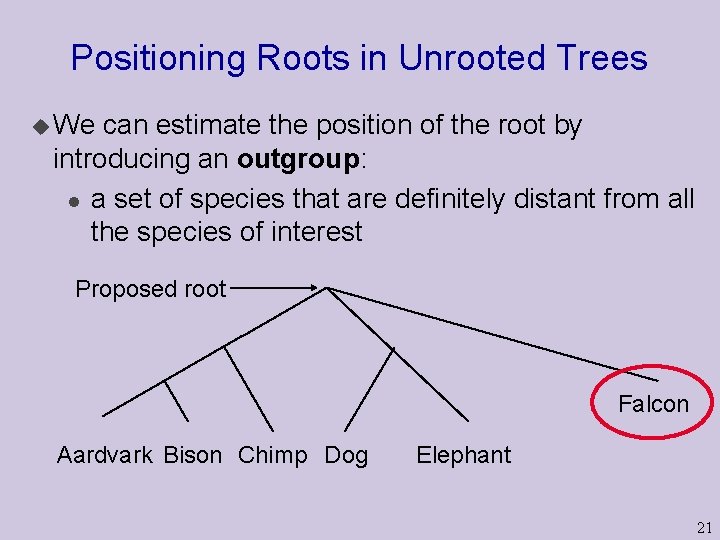
Positioning Roots in Unrooted Trees u We can estimate the position of the root by introducing an outgroup: l a set of species that are definitely distant from all the species of interest Proposed root Falcon Aardvark Bison Chimp Dog Elephant 21

Type of Data u Distance-based l l Input is a matrix of distances between species Can be fraction of residue they disagree on, or alignment score between them, or … u Character-based l Examine each character (e. g. , residue) separately 22

Three Methods of Tree Construction u Distance- A tree that recursively combines two nodes of the smallest distance. u Parsimony – A tree with a total minimum number of character changes between nodes. u Maximum likelihood - Finding the best Bayesian network of a tree shape. The method of choice nowadays. Most known and useful software called phylip uses this method. 23

Distance-Based Method Input: distance matrix between species Outline: u. Cluster species together u. Initially clusters are singletons u. At each iteration combine two “closest” clusters to get a new one 24

Unweighted Pair Group Method using Arithmetic Averages (UPGMA) u UPGMA is a type of Distance-Based algorithm. u Despite its formidable acronym, the method is simple and intuitively appealing. u It works by clustering the sequences, at each stage amalgamating two clusters and, at the same time, creating a new node on the tree. u Thus, the tree can be imagined as being assembled upwards, each node being added above the others, and the edge lengths being determined by the difference in the heights of the nodes at the top and bottom of an edge. 25

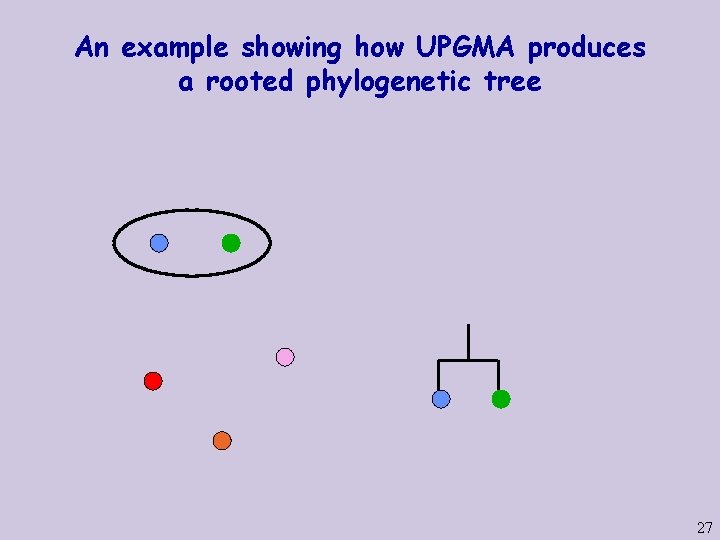
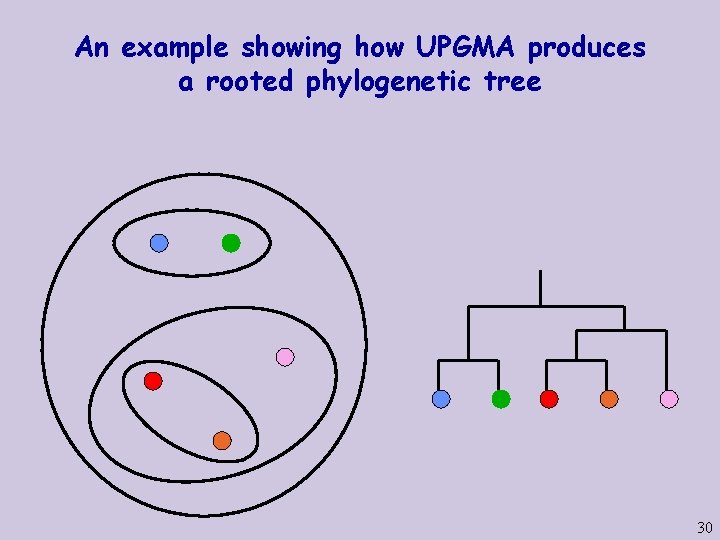
An example showing how UPGMA produces a rooted phylogenetic tree 26

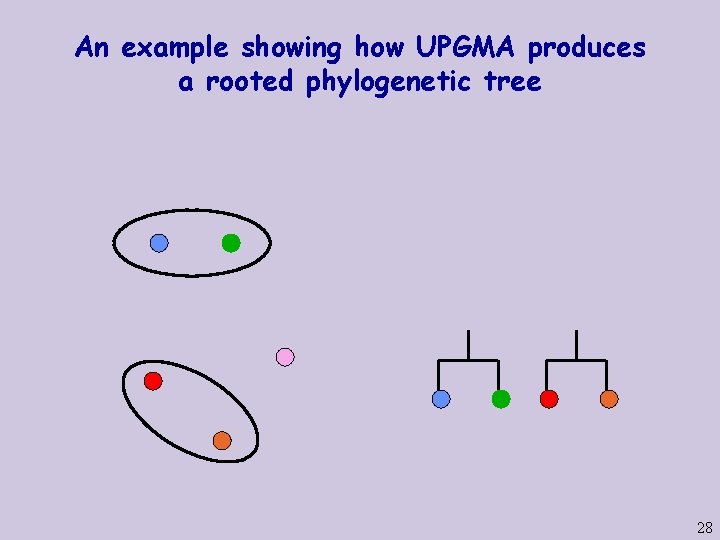
An example showing how UPGMA produces a rooted phylogenetic tree 27

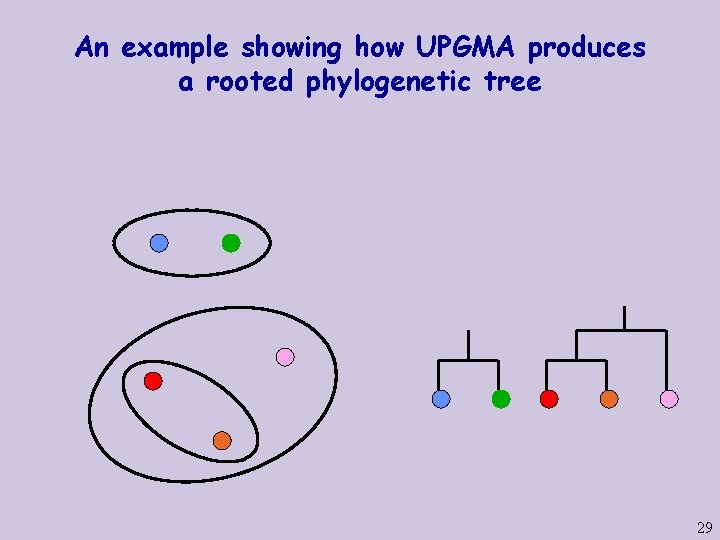
An example showing how UPGMA produces a rooted phylogenetic tree 28

An example showing how UPGMA produces a rooted phylogenetic tree 29

An example showing how UPGMA produces a rooted phylogenetic tree 30

UPGMA Clustering u u u Let Ci and Cj be clusters, define distance between them to be When we combine two cluster, Ci and Cj, to form a new cluster Ck, then Define a node K and place its children nodes at depth d(Ci, Cj)/2 31

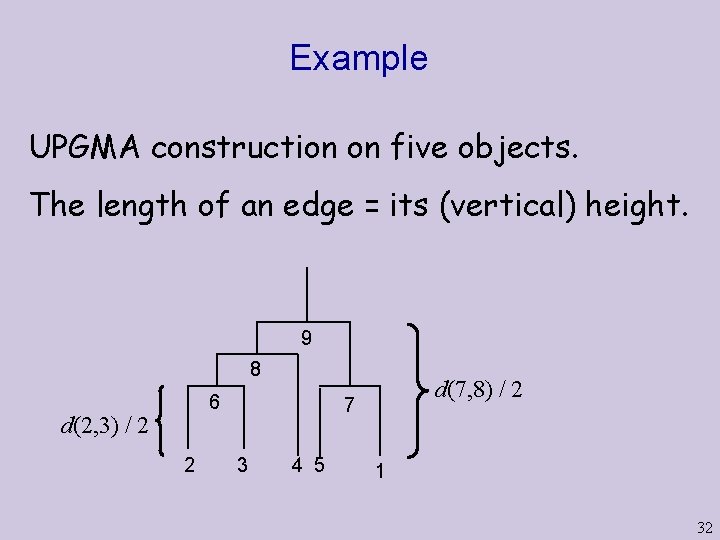
Example UPGMA construction on five objects. The length of an edge = its (vertical) height. 9 8 6 d(2, 3) / 2 2 d(7, 8) / 2 7 3 4 5 1 32

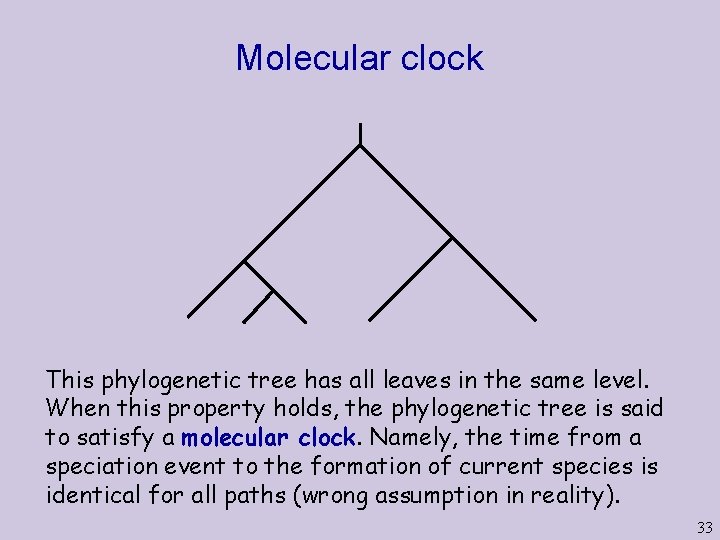
Molecular clock This phylogenetic tree has all leaves in the same level. When this property holds, the phylogenetic tree is said to satisfy a molecular clock. Namely, the time from a speciation event to the formation of current species is identical for all paths (wrong assumption in reality). 33

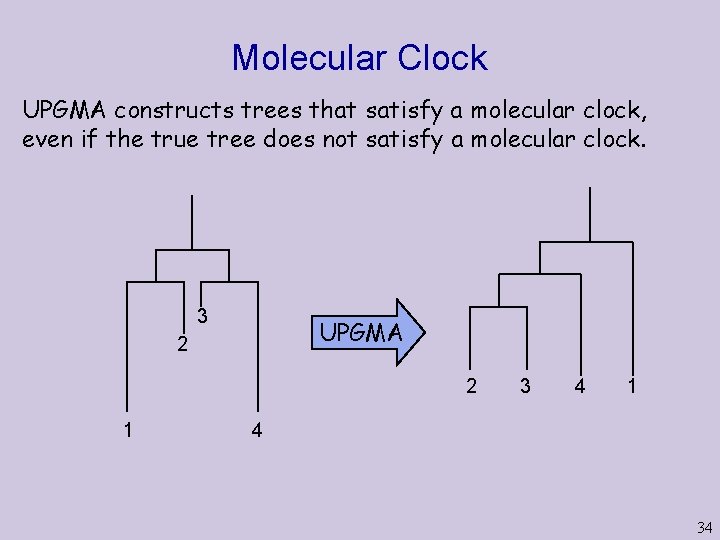
Molecular Clock UPGMA constructs trees that satisfy a molecular clock, even if the true tree does not satisfy a molecular clock. 3 UPGMA 2 2 1 3 4 1 4 34

Restrictive Correctness of UPGMA Proposition: If the distance function is derived by adding edge distances in a tree T with a molecular clock, then UPGMA will reconstruct T. Proof idea: Move a horizontal line from the bottom of the T to the top. Whenever an internal node is formed, the algorithm will create it. 35

Additivity Molecular clock defines additive distances, namely, distances between objects can be realized by a tree: k c a b j i 36

What is a Distance Matrix? Given a set M of L objects with an L× L distance matrix: ud(i, i) = 0, and for i ≠ j, d(i, j) > 0 ud(i, j) = d(j, i). u For all i, j, k, it holds that d(i, k) ≤ d(i, j)+d(j, k). Can we construct a weighted tree which realizes these distances? 37

Additive Distances We say that the set M with L objects is additive if there is a tree T, L of its nodes correspond to the L objects, with positive weights on the edges, such that for all i, j, d(i, j) = d. T(i, j), the length of the path from i to j in T. Note: Sometimes the tree is required to be binary, and then the edge weights are required to be non-negative. 38

Three objects sets are additive: For L=3: There is always a (unique) tree with one internal node. k c a m b j i Thus 39

How about four objects? L=4: Not all sets with 4 objects are additive: e. g. , there is no tree which realizes the below distances. i j i 0 2 2 2 j 0 2 2 0 3 k l 0 40

The Four Points Condition Theorem: A set M of L objects is additive iff any subset of four objects can be labeled i, j, k, l so that: d(i, k) + d(j, l) = d(i, l) +d(k, j) ≥ d(i, j) + d(k, l) We call {{i, j}, {k, l}} the “split” of {i, j, k, l}. k i j l Proof: Additivity 4 P Condition: By the figure. . . 41

4 P Condition Additivity: Induction on the number of objects, L. For L ≤ 3 the condition is empty and tree exists. Consider L=4. B = d(i, k) +d(j, l) = d(i, l) +d(j, k) ≥ d(i, j) + d(k, l) = A Let y = (B – A)/2 ≥ 0. Then the tree should look as follows: We have to find the distances a, b, c and f. k c l f n y a i m b j 42

Tree construction for L = 4 Construct the tree by the given distances as follows: 1. Construct a tree for {i, j, k}, with internal vertex m 2. Add vertex n , d(m, n) = y 3. Add edge (n, l), c+f = d(k, l) k f c Remains to prove: d(i, l) = d. T(i, l) d(j, l) = d. T(j, l) l n a y m b j i 43

Proof for “L = 4” By the 4 points condition and the definition of y : d(i, l) = d(i, j) + d(k, l) +2 y - d(k, j) = a + y + f = d. T(i, l) (the middle equality holds since d(i, j), d(k, l) and d(k, j) are realized by the tree) d(j, l) = d. T(j, l) is proved similarly. k f c B = d(i, k) +d(j, l) = d(i, l) +d(j, k) ≥ d(i, j) + d(k, l) = A, y = (B – A)/2 ≥ 0. l n a y m b j i 44

Induction step for “L > 4” : u Remove Object L from the set u By induction, there is a tree, T’, for {1, 2, … , L-1}. u For each pair of labeled nodes (i, j) in T’, let aij, bij, cij be defined by the following figure: L cij aij mij bij j i 45

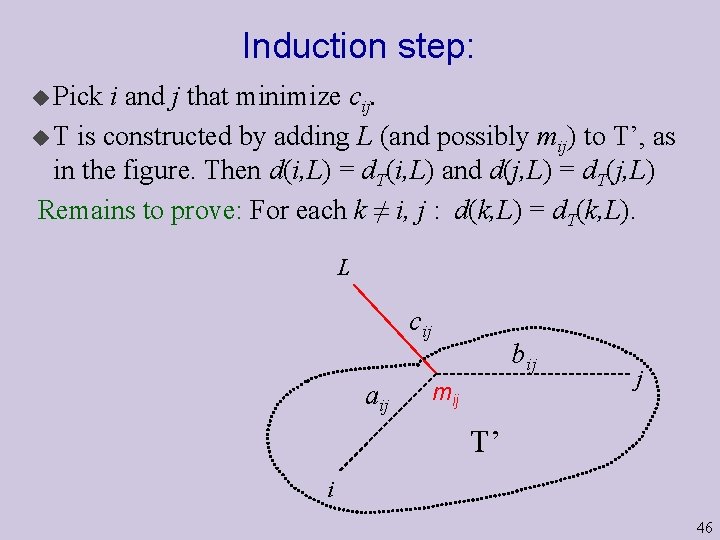
Induction step: u Pick i and j that minimize cij. u T is constructed by adding L (and possibly mij) to T’, as in the figure. Then d(i, L) = d. T(i, L) and d(j, L) = d. T(j, L) Remains to prove: For each k ≠ i, j : d(k, L) = d. T(k, L). L cij aij bij mij j T’ i 46

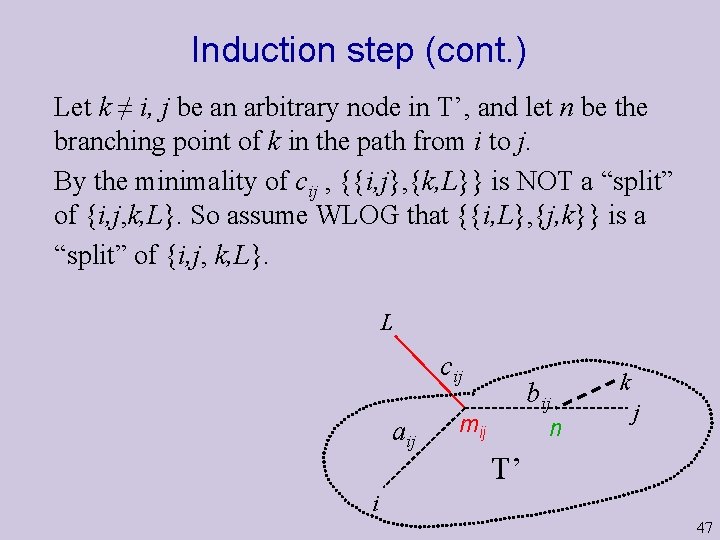
Induction step (cont. ) Let k ≠ i, j be an arbitrary node in T’, and let n be the branching point of k in the path from i to j. By the minimality of cij , {{i, j}, {k, L}} is NOT a “split” of {i, j, k, L}. So assume WLOG that {{i, L}, {j, k}} is a “split” of {i, j, k, L}. L cij aij bij mij n k j T’ i 47

Induction step (end) Since {{i, L}, {j, k}} is a split, by the 4 points condition d(L, k) = d(i, k) + d(L, j) - d(i, j) d(i, k) = d. T(i, k) and d(i, j) = d. T(i, j) by induction hypothesis, and d(L, j) = d. T(L, j) by the construction. Hence d(L, k) = d. T(L, k). QED L cij aij bij mij k n j T’ i 48