La corrlation et la rgression Mesure de la

La corrélation et la régression

Mesure de la relation entre deux variables n 2 variables sont prises en considération simultanément n n n Attention, ce n’est jamais un indice de cause à effet n n -> manipulations expérimentales La relation est décrite par le coefficient de corrélation (r) n n Ex. Résultats en français et en mathématique Couleur d’une auto et le nombre d’accidents Il varie entre -1 et 1: 1 (ou -1) = relation parfaite 0 = absence de relation Il existe donc trois cas possibles: n n n Relation positive : x augmente; y augmente Relation négative : x diminue; y augmente Absence de relation: x augmente (ou diminue); y ne change pas

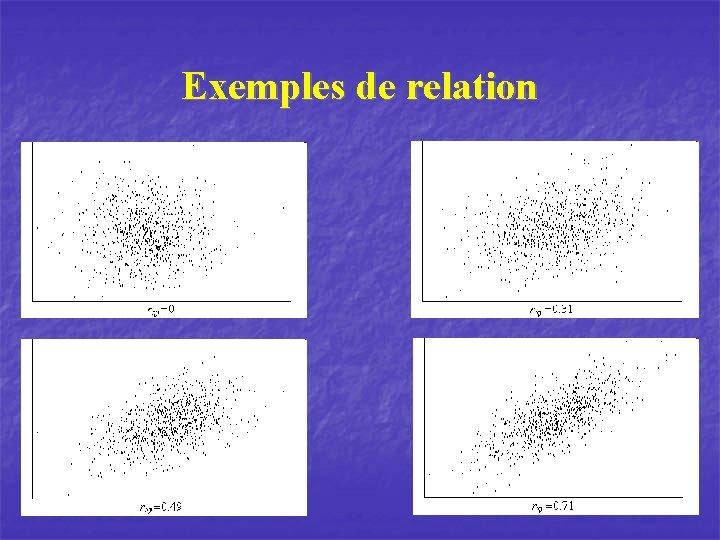
Exemples de relation

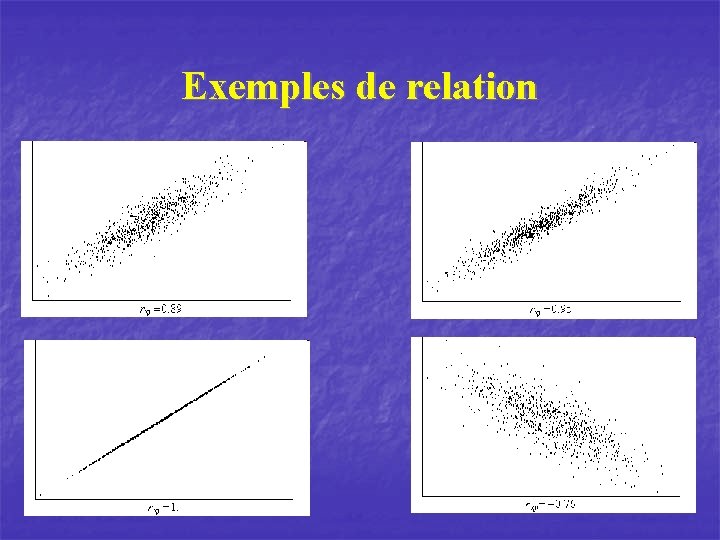
Exemples de relation

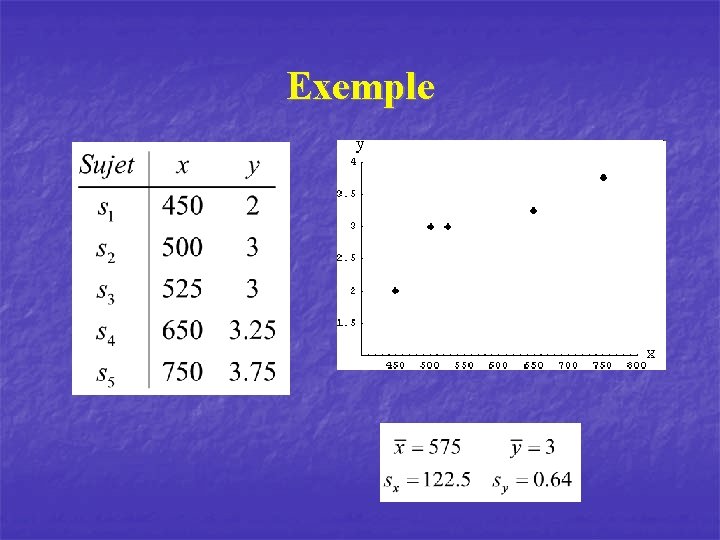
Exemple

Exemple Mesure la direction et la grandeur de la relation

Note

Exemple Comme on ne peut pas comparer des mesures de covariances entrent-elles, il faut la standardiser.

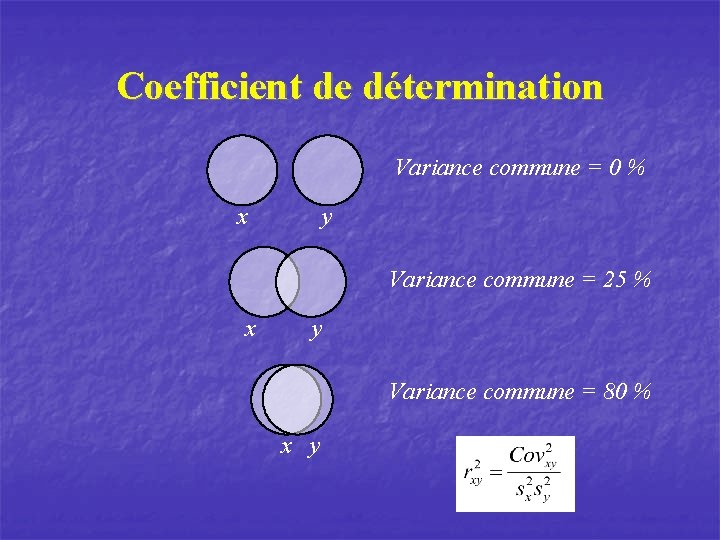
Coefficient de détermination Variance commune = 0 % x y Variance commune = 25 % x y Variance commune = 80 % x y

Exemple 77% de la variance en y peut être expliquée par la variance en x Exemple 2 (SAT) 36% de la variance de la réussite universitaire peut être expliquée par la variance du score au SAT

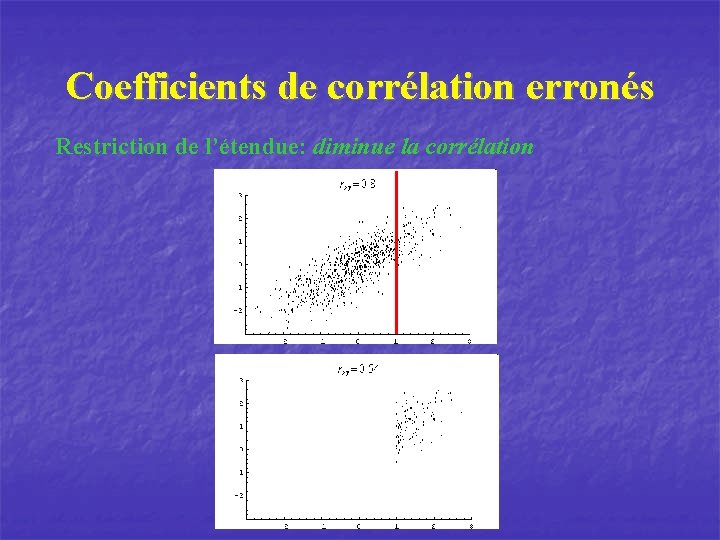
Coefficients de corrélation erronés Restriction de l’étendue: diminue la corrélation

Coefficients de corrélation erronés Utilisation de groupes extrêmes: augmente la corrélation L L L L L r = 0. 75 H H H H H

Coefficients de corrélation erronés Utilisation de groupes extrêmes: augmente la corrélation r = 0. 50 x L x x x L LL L L x x x L L x xx x x L x x x H H x x H HH H x x x H H x x H

Coefficients de corrélation erronés Combiner des groupes: augmente ou diminue la corrélation r 2 = 0 r 1 = 0 > 0 r 2 > r 2 0 r 1 > 0

Coefficients de corrélation erronés Score extrême: augmente ou diminue la corrélation x xxx xx xx x x x

Coefficients de corrélation erronés Relation non linéaire: diminue la corrélation

Note n Même si le coefficient de corrélation est celui rapporté, il n’est pas un estimateur non biaisé de la corrélation dans la population. Plus, l’échantillon est petit, plus le biais sera grand. Pour corriger la situation, le coefficient de corrélation ajusté est calculé.

Inférence

Inférence n L’hypothèse émise est que la corrélation entre x et y est nulle dans la population. Autrement dit, on cherche à savoir si x et y sont linéairement indépendants. Si on rejette cette hypothèse, alors cela indique les populations ne sont pas indépendantes et qu’il existe une relation linéaire entre les deux. Ou

Exemple Comme le tobs >tcrit (3. 209>3. 182) on rejette H 0 et on accepte H 1. Les 2 populations sont donc dépendantes.

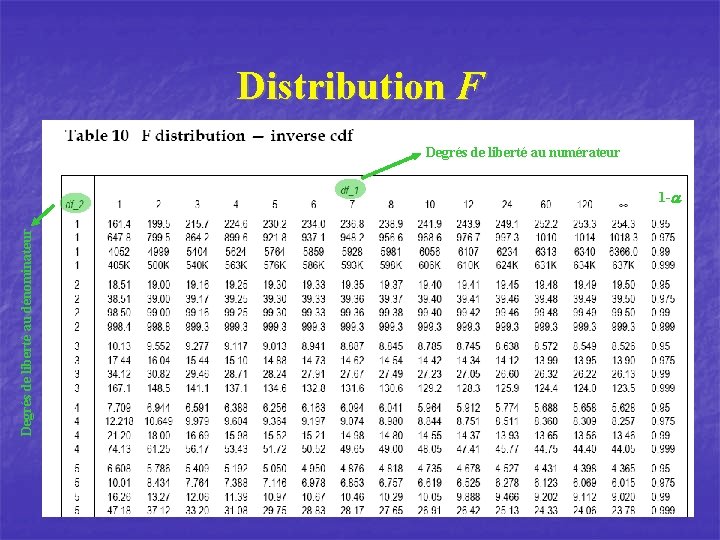
Distribution F Degrés de liberté au numérateur Degrés de liberté au dénominateur 1 -a

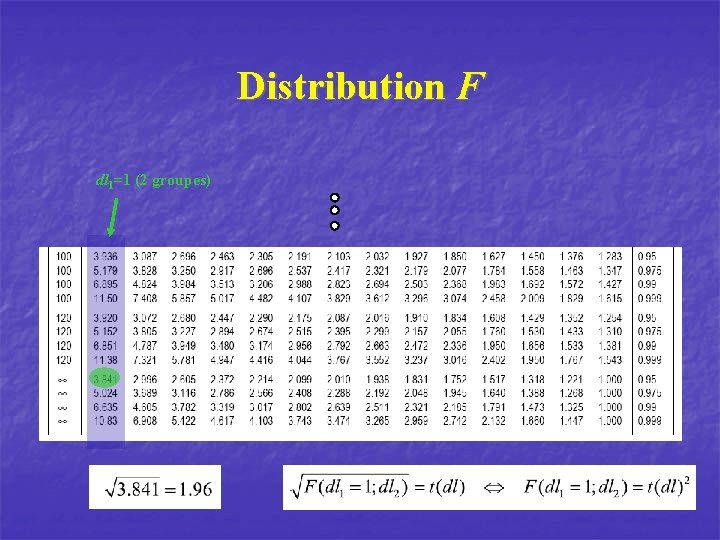
Distribution F dl 1=1 (2 groupes)

Exemple (F) Comme le Fobs >Fcrit (10. 37>10. 13) on rejette H 0 et on accepte H 1. Les 2 populations sont donc dépendantes.

Régression linéaire

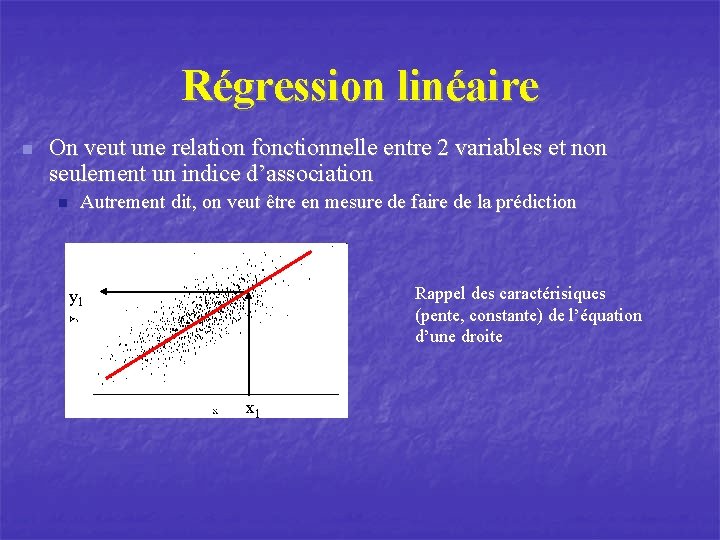
Régression linéaire n On veut une relation fonctionnelle entre 2 variables et non seulement un indice d’association n Autrement dit, on veut être en mesure de faire de la prédiction Rappel des caractérisiques (pente, constante) de l’équation d’une droite y 1 x 1

Les paramètres de la droite de régression Si on remplace b 0

Note On sait que Si on remplace la covariance par sa valeur

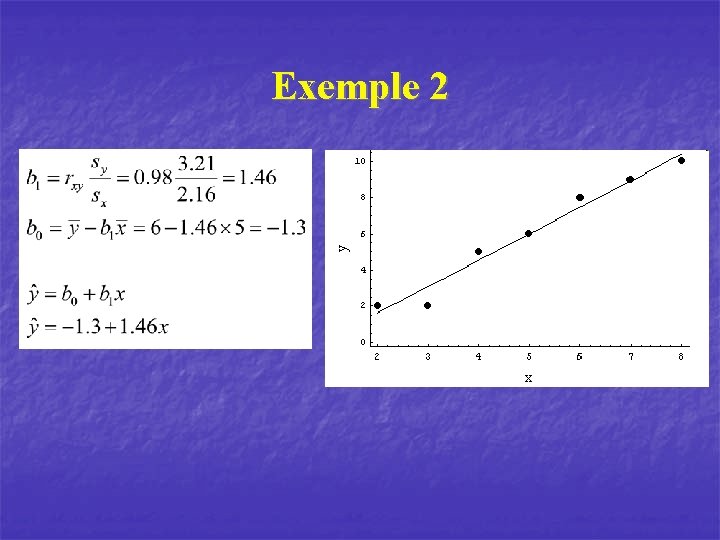
Exemple 2

Exemple 2

Prédiction n À partir de l’équation de régression, il est possible de faire des prédiction Ex. 1 Si x = 7. 5, que vaut ?

Prédiction n De façon similaire on peut prédire x à partie de y Ex. 2 Si y = 9. 65, que vaut ?

Prédiction n Enfin! Ex. 3 n Si x = 3, que vaut ? Or, (x, y) => (3, 2). Donc, la prédiction commet une certaine erreur

Erreur type de la régression n La différence entre la droite de régression constitue l’erreur de prédiction à partir de x.

Note Pour des grands échantillons

Intervalles de confiance Prédiction à partir d’un nouveau score n L’erreur type est un estimé de l’erreur totale. Cependant il n’est pas un bon estimé pour la prédiction d’un x donné. En effet, l’estimation de l’erreur sera plus petite lorsque x est près de la moyenne et plus grande lorsqu’il est loin de la moyenne.

Intervalles de confiance Prédiction à partir d’un nouveau score n Exemple xnew= 7. 5 pour un IC de 95%

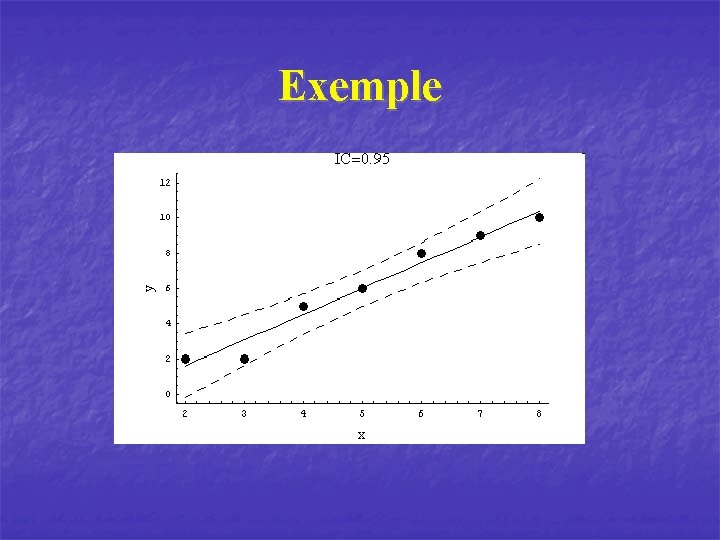
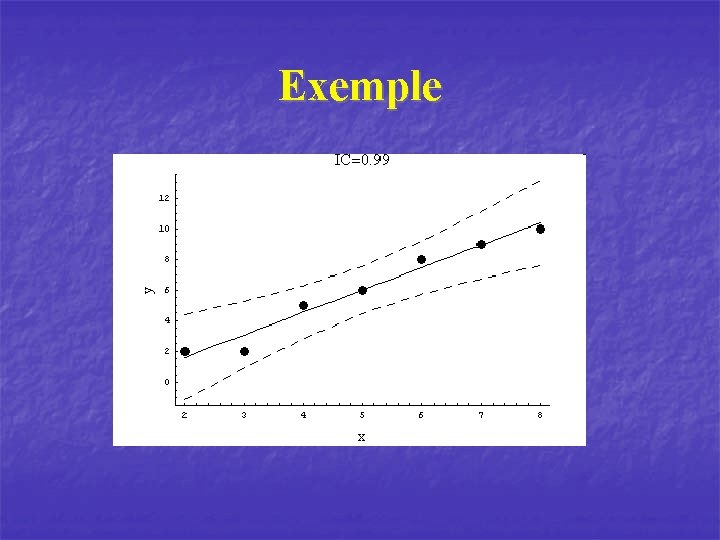
Intervalles de confiance Prédiction pour l’ensemble des données n Il peut être intéressant de connaître la région de confiance pour l’ensemble de la droite de régression.

Exemple

Exemple

Exemple

Relation entre le test t et la corrélation

Exemple (groupes indépendants) Test t

Exemple (groupes indépendants) Modèle général linéaire (corrélation) L’idée est de construire une variable indépendante qui permettra d’identifier à quel groupe appartient la variable dépendante. Ex 1: 1 = le premier groupe et 0 le deuxième Ex 2: 1 = le premier groupe et -1 le deuxième

Exemple (groupes indépendants) 1 = le premier groupe et -1 = le deuxième

Exemple (groupes indépendants) Modèle général linéaire (corrélation) Donc, le test t (indépendant) est un cas particulier de la corrélation/régression

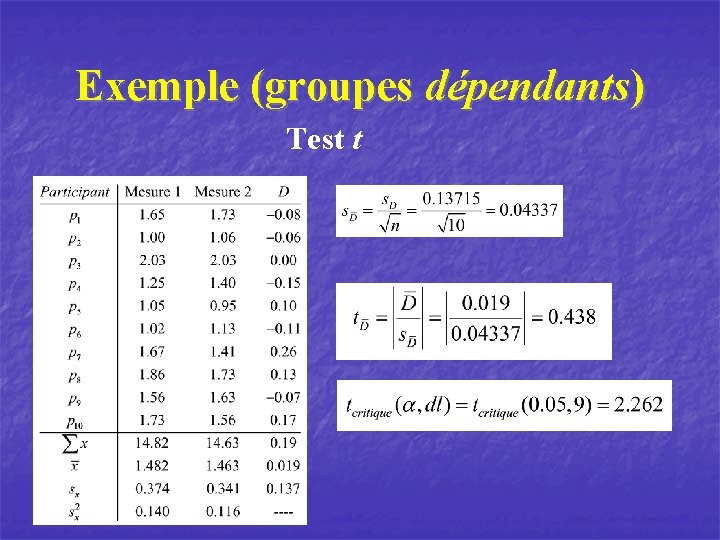
Exemple (groupes dépendants) Test t

Exemple (groupes dépendants) Modèle général linéaire (corrélation) L’idée est de décomposer la variabilité en deux parties. Ainsi, dans le schème à mesures répétées il y a une part de variabilité attribuable aux sujets et une autre à la condition (effet possible de traitement).

Exemple (groupes dépendants) Modèle général linéaire (corrélation) Variabilité des sujets Pour estimer cette variabilité on élimine l’effet condition:

Exemple (groupes dépendants) Modèle général linéaire (corrélation) Variabilité des sujets Pour estimer cette variabilité on élimine l’effet condition:

Exemple (groupes dépendants) Modèle général linéaire (corrélation) Variabilité de la condition Pour estimer cette variabilité on élimine l’effet mesure répétée; on procède comme si les groupes étaient indépendants:

Exemple (groupes dépendants) Modèle général linéaire (corrélation) Test de signification

Exemple (groupes dépendants) Modèle général linéaire (corrélation) Donc, le test t (dépendant) est aussi un cas particulier de la corrélation/régression