Kvantitatv mdszerek 1 Valsznsgszmtsi alapok Dr Kvesi Jnos

Kvantitatív módszerek 1. Valószínűségszámítási alapok Dr. Kövesi János Készítette: Erdei János

A valószínűségszámítás tárgya n Véletlen jelenség fogalma n Tömegjelenség fogalma Készítette: Erdei János

A valószínűség fogalma A Készítette: Erdei János n f(A)

Az axiómarendszer 1. axióma 0 P(A) 2. axióma P( ) = 1 3. axióma Ha A 1, A 2, … An páronként kizárják egymást, akkor P(A 1 + A 2 +. . . An) = P(A 1) + P(A 2) + … + P(An) Teljes eseményrendszer: P(A 1 + A 2 +. . . An) = P( ) = 1 Készítette: Erdei János

A valószínűség meghatározásának módszerei Klasszikus valószínűség-meghatározás n Geometriai n Valószínűségszámítási tételek n Empirikus adatokból n Elméleti eloszlások n Szubjektív becslés n Készítette: Erdei János

Valószínűségszámítás fő területei Készítette: Erdei János

Kvantitatív módszerek 2. Valószínűségszámítási tételek Dr. Kövesi János Készítette: Erdei János

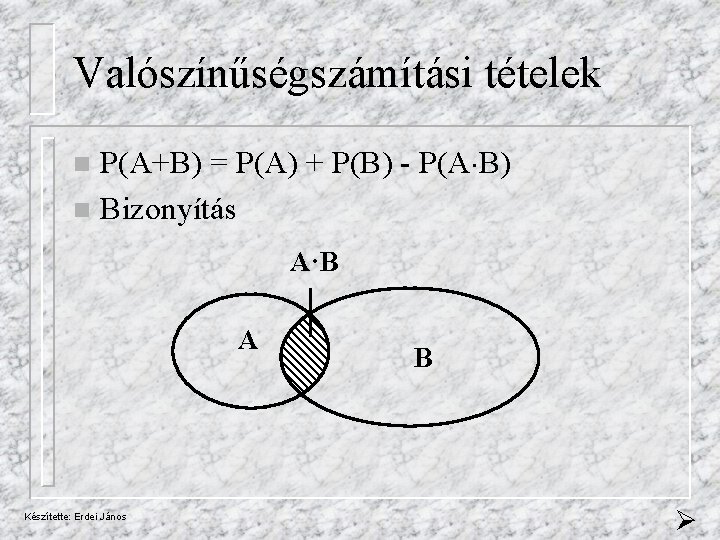
Valószínűségszámítási tételek P(A+B) = P(A) + P(B) - P(A B) n Bizonyítás n A·B A Készítette: Erdei János B

Valószínűségszámítási tételek n Ha A esemény bekövetkezése. . . – – n P(B-A) = P(B) - P(A) és P(A) P(B) Bizonyítás: B = A + (B-A) P(B) = P(A) + P(B-A) Mivel P(B-A) 0 Készítette: Erdei János III. axióma P(A) P(B)

Valószínűségszámítási tételek 1. Feladat: Mutassuk ki, hogy. . . P(A+B) = P(A) + P(B) - P(A+B) 0, 7 0, 9 +1 a lehetséges legnagyobb értéke 2. Feladat: Próbagyártás után. . . P(A + B) = 0, 15 + 0, 3 - 0, 08 = 0, 37 P(A + B) = 0, 63 Készítette: Erdei János

Valószínűségszámítási tételek 3. Feladat: Egy iskola tanulóinál. . . P(A) = P(A + B) + P(A B) - P(B) = = 0, 16 + 0, 09 - 0. 11 = 0, 14 Készítette: Erdei János

A feltételes valószínűség fogalma Definíció: Ha A és B … P(A|B) = P(A B) / P(B) Legyen A és B egy kísérlettel kapcsolatos két esemény, és P(B) 0 Készítette: Erdei János

A feltételes valószínűség fogalma 1. Feladat: Egy szállítmány 96%-a … A = a termék I. o. } B = a termék megfelelő} P(AB) = P (A|B) · P(B) = 0, 75 · 0, 96 = 0, 72 Készítette: Erdei János

A feltételes valószínűség fogalma 2. Feladat : Egy telefonfülke előtt állunk … a. ) b. ) c. ) Készítette: Erdei János

A teljes valószínűség tétele Ha B 1, B 2, … Bn teljes …. Bizonyítás: Készítette: Erdei János

A teljes valószínűség tétele 1. Feladat: A magyar nyelvű MBA programban … A = a vizsga sikeres} B 1 = a hallgató férfi} P(B 1) = 0, 45 B 2 = a hallgató nő} P(B 2) = 0, 55 P(A) = 0, 6 · 0, 45 + 0, 8 · 0, 55 = 0, 71 Készítette: Erdei János

A teljes valószínűség tétele 2. Feladat: Három műszak azonos … P(B 1) = 0, 4 P(B 2) = 0, 3 P(B 3) = 0, 3 P(A|B 1) = 0, 95 P(A|B 2) = 0, 93 P(A|B 3) = 0, 90 P(A) = 0, 929 Készítette: Erdei János

Bayes-tétel Ha B 1, B 2, … Bn teljes eseményrendszer …. Készítette: Erdei János

Bayes-tétel Bizonyítás: P(Bk|A)·P(A) = P(A| Bk) ·P(Bk) P(Bk·A) P(A·Bk) Teljes valószínűség tétele Készítette: Erdei János

Bayes-tétel 1. Feladat: Alkatrész-ellátásnál …. A = az alkatrész hibás} B 1 = ”A”-tól jött} P(A|B 1) = 0, 1 B 2 = ”B”-től jött} P(A|B 2) = 0, 2 Készítette: Erdei János

Bayes-tétel 2. Feladat: Egy üzemből kikerülő …. A = a termék I. o. minősítést kap} B 1 = a termék I. o. } P(B 1) = 0, 75 B 2 = a termék nem I. o. } P(B 2) = 0, 25 P (A|B 1) = 0, 98 P (A|B 2) = 0, 05 Készítette: Erdei János

Bayes-tétel 3. Feladat: Egy folyóban bekövetkező …. Bi = az i-edik üzemet terheli a felelősség} (A |Bi) = halpusztulás következett be, feltéve, hogy Bi volt a szennyező} P(B 1)=0, 2 P(B 2)=0, 5 P(B 3)=0, 3 P(A |B 1)=0, 6 P(A |B 2)=0, 15 P(A |B 3)=0, 25 Készítette: Erdei János

Bayes-tétel 3. Feladat: folyt. P(A)=0, 2· 0, 6+0, 5· 0, 15+0, 3 · 0, 25 = 0, 27 P(B 1|A)=0, 44 1, 1 MFt Készítette: Erdei János P(B 2|A)=0, 28 700 e. Ft P(B 3|A)=0, 28 700 e. Ft

Események függetlensége Definíció: Készítette: Erdei János

Kvantitatív módszerek 3. Leíró statisztika Dr. Kövesi János Készítette: Erdei János

Statisztikai leírás alapjai A statisztikai leírás célja, módszerei n Statisztikai leírás mutatói n · · · n Középértékek Ingadozásmutatók Egyéb mutatók Grafikus kép Készítette: Erdei János

Adatok rendezése, ábrázolása Osztálybasorolás n Gyakoriságok (fi) megállapítása n Relatív gyakoriság (gi) megállapítása n Összegzett (kumulált) gyakoriságok ill. relatív gyakoriságok n Gyakorisági táblázat n Grafikus ábrázolás n Készítette: Erdei János

Feladat - 1 Egy folyamatos üzemben …. Gyakorisági táblázat készítése - Legkisebb és legnagyobb értékek megkeresése - Gyakoriságok meghatározása 0 1 : Készítette: Erdei János

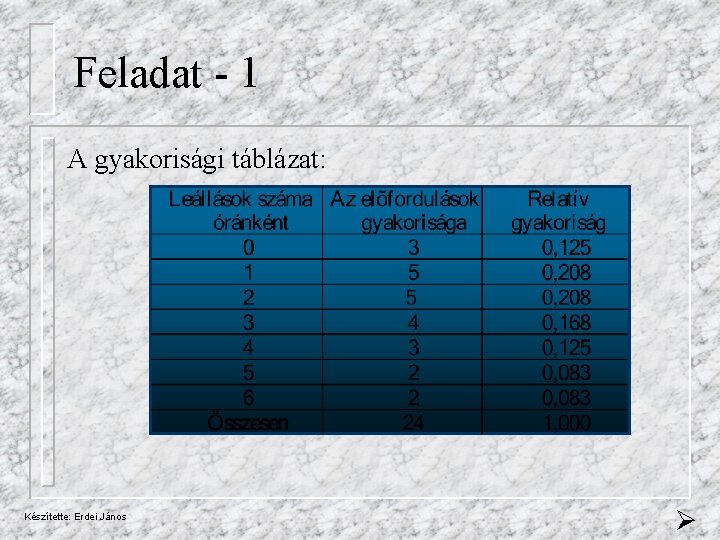
Feladat - 1 A gyakorisági táblázat: Készítette: Erdei János

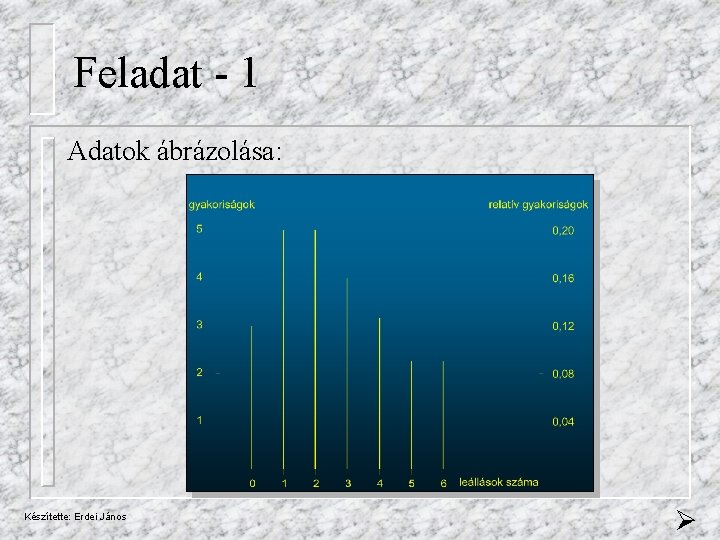
Feladat - 1 Adatok ábrázolása: Készítette: Erdei János

Feladat - 1 A gyakorisági táblázat folytatása: Készítette: Erdei János

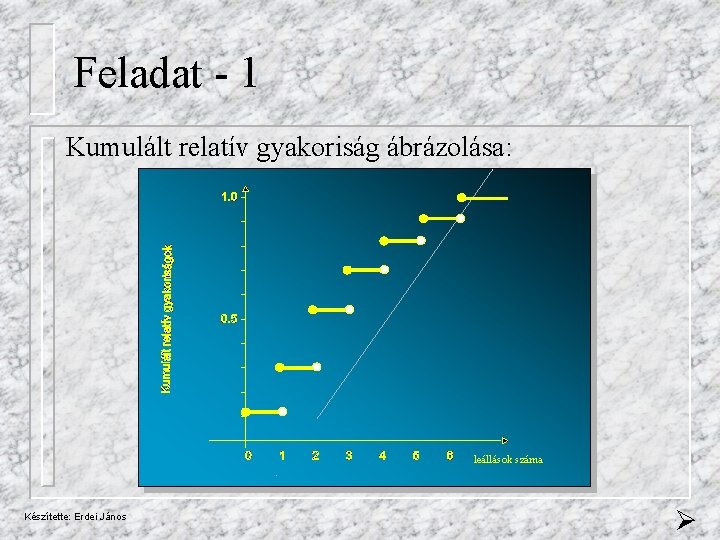
Feladat - 1 Kumulált relatív gyakoriság ábrázolása: leállások száma Készítette: Erdei János

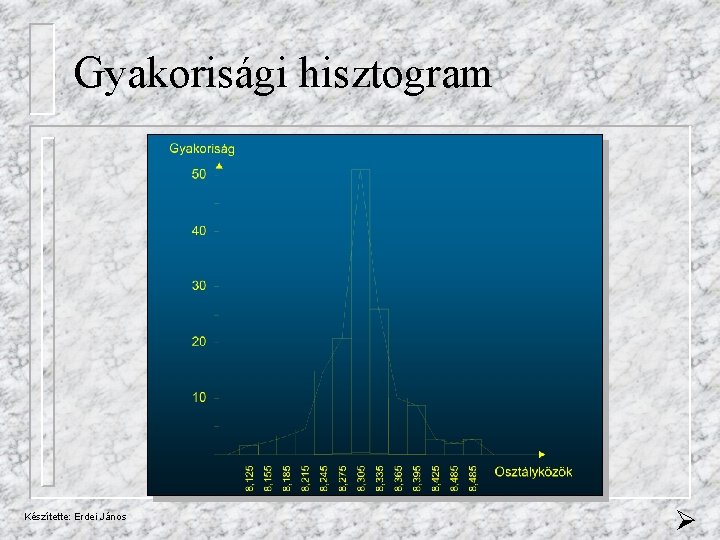
Feladat - 2 Műszeralkatrészek átmérőjét …. Gyakorisági táblázat készítése: - Minimum és maximum értékek keresése - Terjedelem meghatározása: R = 8, 50 - 8, 13 = 0, 37 - Osztályok számának meghatározás - Osztályhatárok, -közepek számolása 8, 13 8, 50 - Gyakoriságok meghatározása - Táblázat és a hisztogram elkészítése Készítette: Erdei János

Gyakorisági hisztogram Készítette: Erdei János

Kumulált relatív gyakoriság Osztályközök [mm] Készítette: Erdei János

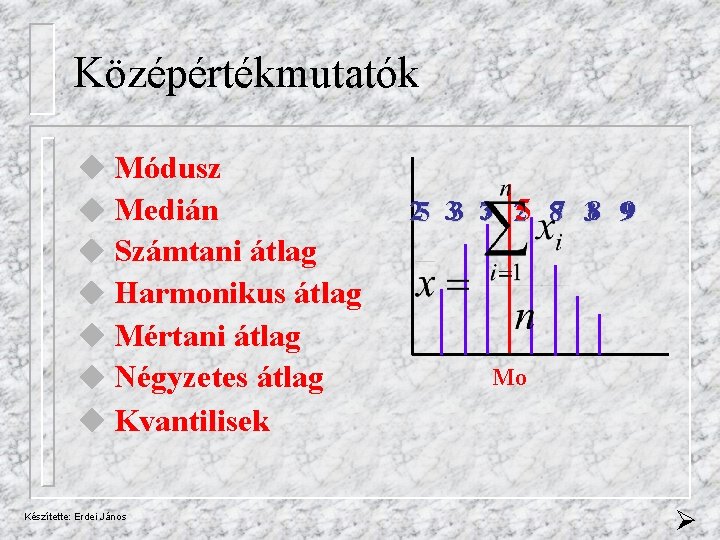
Középértékmutatók Módusz Medián Számtani átlag Harmonikus átlag Mértani átlag Négyzetes átlag 25 33 73 25 87 38 99 Mo Kvantilisek Készítette: Erdei János

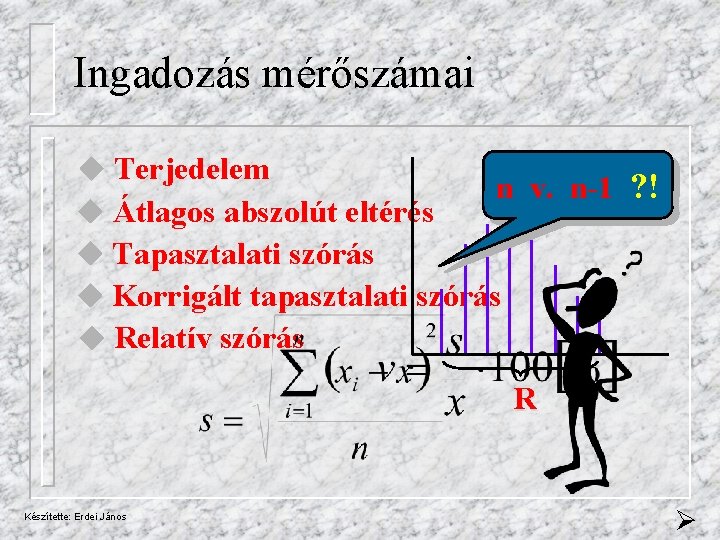
Ingadozás mérőszámai Terjedelem Átlagos abszolút eltérés Tapasztalati szórás n v. n-1 ? ! Korrigált tapasztalati szórás Relatív szórás R Készítette: Erdei János

Készítette: Erdei János