Kvantitatv mdszerek Dntsi osztlyok dntsi kritriumok Gyakorl feladatok

Kvantitatív módszerek Döntési osztályok – döntési kritériumok Gyakorló feladatok

Döntéselmélet – Példa 1 • A Korman Industries olyan zenei cd-ket állít elő, amelyeket postai úton juttatnak el a közönségnek. Méretgazdaságossági és ütemezési problémák miatt a Korman üzletpolitikája az, hogy egy adott hanganyagból legyártani szánt példányokat egyetlen termelési ütem alatt állítják elő. Ha a piaci kereslet nagyobb, mint a legyártott mennyiség, akkor a vevők (akik megrendelték, de nem jutott cd) egy 4$-os kupont kapnak, amelyet a vevő bármelyik más cd megvásárlásakor felhasználhat. Ha a legyártott mennyiség meghaladja a piaci keresletet, akkor a fennmaradó cd-ket 5$ért adják el egy zenei áruháznak. Ez az 5$ éppen egy cd változó költségének a fele. • A Korman egy újonnan kötött megállapodás értelmében most fizetett 200000$-nyi jogdíjat egy adott hanganyagért, amelyről készült cd-t 50$-ért kívánja majd értékesíteni. A piackutató részlegük előrejelzése szerint az alábbi piaci keresleti szintek fordulhatnak elő: 20000, 40000, 60000, és 80000 db. • Fix költség: 200000$, változó költség: 10$/db

Döntéselmélet – Példa 1 a) Készítsük el a döntési mátrixot! Tételezzük fel, hogy nincs információnk a piaci keresleti szint valószínűségéről! Hogyan döntsön a szervezet ebben a helyzetben? Milyen kritériumokat alkalmazhat? b) Tételezzük fel, hogy a korábbi tapasztalatok alapján a következő valószínűségek rendelhetők az egyes keresleti szintekhez: 0, 1; 0, 3; 0, 4; 0, 2. Hogyan döntsön ilyen helyzetben? c) A vállalatvezetés úgy döntött, hogy csak akkor veszi meg a jogdíjat, ha várhatóan 60000 db-ot el tud adni a cd-ből. A piackutató részleg gyorsfelmérést végzett. A részleg által adott előrejelzés az esetek 65%ában jelezte előre helyesen a 60000 db eladását. A piackutató részleg 20000 db keresleténél 10%-ban jelezte a 60000 db eladását, 40000 db keresleténél 15%-ban és 80000 db keresleténél pedig 10%-ban. d) Mekkora valószínűséggel veszi meg a jogdíjat? e) Hosszú távon mekkora profitja lesz a cd-k eladásából a vállalatnak?

Megoldás – Példa 1 • Pénzügy eredmény= Ár 1 * x + -fix költség –változó költség * x (+többletbevétel/extraköltség) t 1: 20000 s 1: 20000 600000 s 2: 40000 500000 s 3: 60000 400000 t 2: 40000 520000 1400000 1300000 t 3: 60000 440000 1320000 2200000 t 4: 80000 360000 1240000 2120000 s 4: 80000 300000 1200000 2100000 3000000

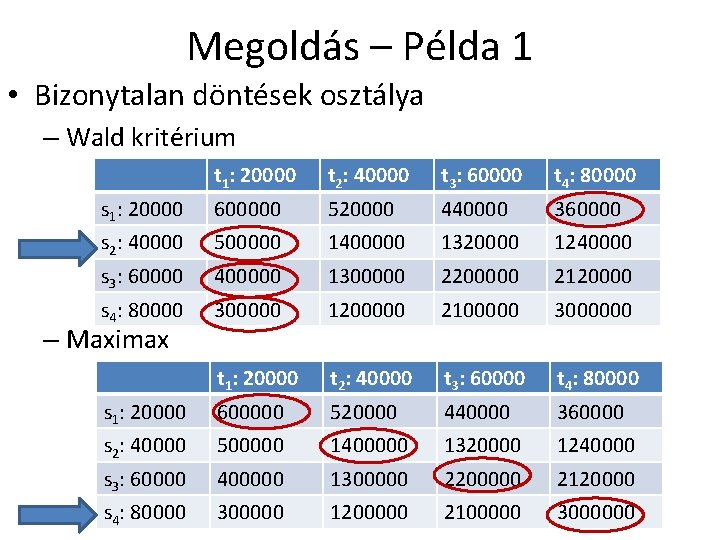
Megoldás – Példa 1 • Bizonytalan döntések osztálya – Wald kritérium t 1: 20000 t 2: 40000 t 3: 60000 t 4: 80000 s 1: 20000 600000 520000 440000 360000 s 2: 40000 500000 1400000 1320000 1240000 s 3: 60000 400000 1300000 2200000 2120000 s 4: 80000 300000 1200000 2100000 3000000 – Maximax

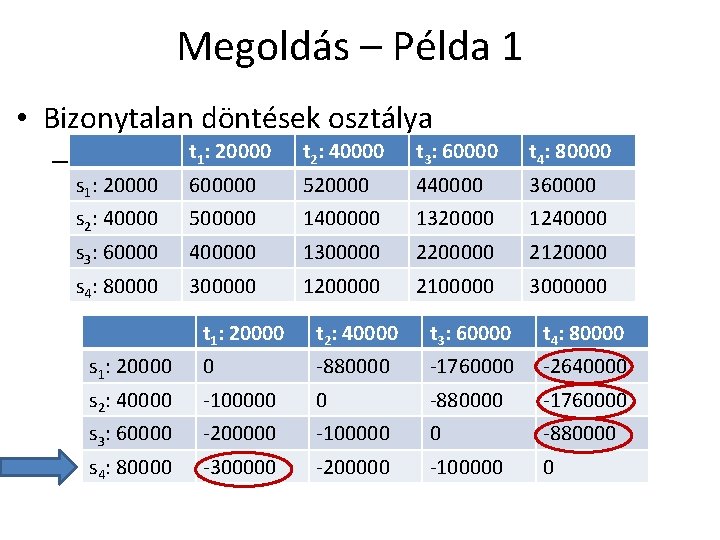
Megoldás – Példa 1 • Bizonytalan döntések osztálya t 1: 20000 t 2: 40000 t 3: 60000 t 4: 80000 s 1: 20000 600000 520000 440000 360000 s 2: 40000 500000 1400000 1320000 1240000 s 3: 60000 400000 1300000 2200000 2120000 s 4: 80000 300000 1200000 2100000 3000000 – Savage t 1: 20000 t 2: 40000 t 3: 60000 t 4: 80000 s 1: 20000 0 -880000 -1760000 -2640000 s 2: 40000 -100000 0 -880000 -1760000 s 3: 60000 -200000 -100000 0 -880000 s 4: 80000 -300000 -200000 -100000 0

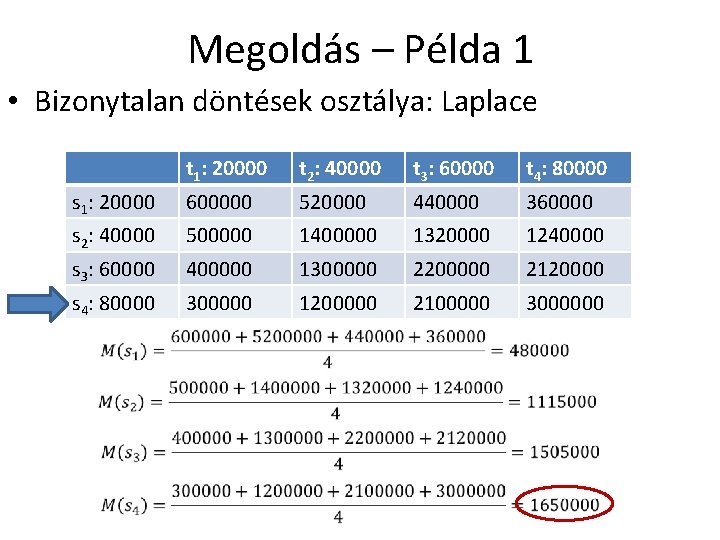
Megoldás – Példa 1 • Bizonytalan döntések osztálya: Laplace t 1: 20000 t 2: 40000 t 3: 60000 t 4: 80000 s 1: 20000 600000 520000 440000 360000 s 2: 40000 500000 1400000 1320000 1240000 s 3: 60000 400000 1300000 2200000 2120000 s 4: 80000 300000 1200000 2100000 3000000

Megoldás – Példa 1 • Bizonytalan döntések osztálya: Hurwicz – Legyen az optimizmus együttható: 0, 8 t 1: 20000 t 2: 40000 t 3: 60000 t 4: 80000 s 1: 20000 600000 520000 440000 360000 s 2: 40000 500000 1400000 1320000 1240000 s 3: 60000 400000 1300000 2200000 2120000 s 4: 80000 300000 1200000 2100000 3000000

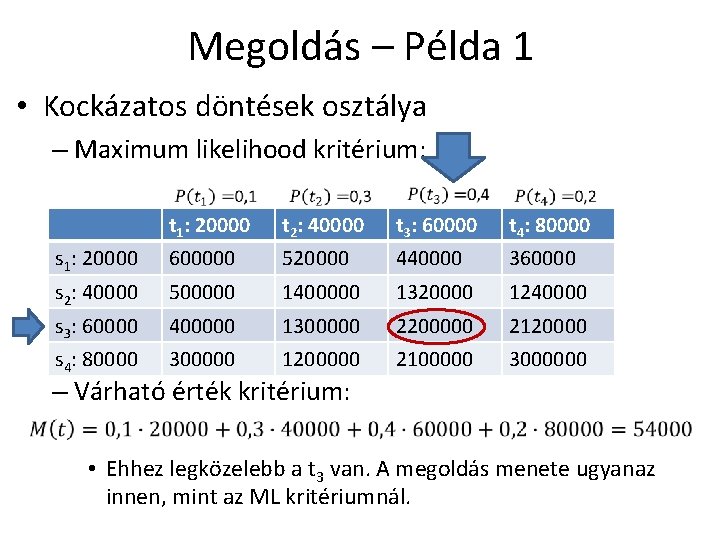
Megoldás – Példa 1 • Kockázatos döntések osztálya – Maximum likelihood kritérium: t 1: 20000 t 2: 40000 t 3: 60000 t 4: 80000 s 1: 20000 600000 520000 440000 360000 s 2: 40000 500000 1400000 1320000 1240000 s 3: 60000 400000 1300000 2200000 2120000 s 4: 80000 300000 1200000 2100000 3000000 – Várható érték kritérium: • Ehhez legközelebb a t 3 van. A megoldás menete ugyanaz innen, mint az ML kritériumnál.

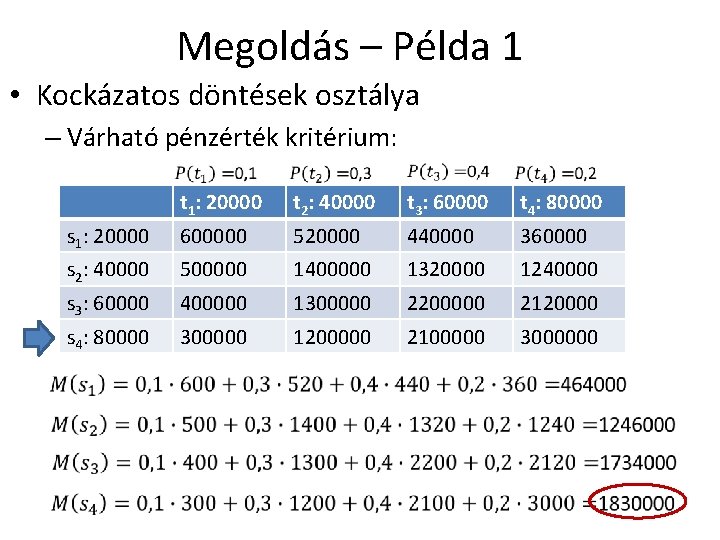
Megoldás – Példa 1 • Kockázatos döntések osztálya – Várható pénzérték kritérium: t 1: 20000 t 2: 40000 t 3: 60000 t 4: 80000 s 1: 20000 600000 520000 440000 360000 s 2: 40000 500000 1400000 1320000 1240000 s 3: 60000 400000 1300000 2200000 2120000 s 4: 80000 300000 1200000 2100000 3000000

Megoldás – Példa 1 • Kockázatos döntés pótlólagos információk alapján Z esemény: a piackutató 60000 dbot jelez előre A priori val. Felt. val. Posteriori val. (Bayes tétel)

Megoldás – Példa 1 t 1: 20000 t 2: 40000 t 3: 60000 t 4: 80000 s 1: 20000 600000 520000 440000 360000 s 2: 40000 500000 1400000 1320000 1240000 s 3: 60000 400000 1300000 2200000 2120000 s 4: 80000 300000 1200000 2100000 3000000

Döntéselmélet – Példa 2 • A Santa Claus Tree Company megszerezte a bérleti jogát egy olyan területnek, ahol akár 1 millió db fenyőfa kivágására is lehetősége nyílik. A vállalatnak döntenie kell, hogy hány fát vágjon ki és szállítson le az értékesítési helyeire december folyamán. Ha a vállalat keveset vág ki, akkor potenciális bevételtől eshet el, ha pedig a keresletnél többet vág ki, akkor a kivágás és szállítás költségeivel kell számolnia az el nem adott fák esetében. Karácsony után pedig nyilván nincs kereslet e fenyőfákra. • A terület bérleti díja 50000$/év + a bérleti díj változó része: 2$/fa. Egy fenyő kivágásának és szállításának további becsült költsége 1$/fa. Keresleti szint Valószínűség A marketing részleg előrejelzése szerint a keresleti viszonyok és azok valószínűsége az alábbiak szerint alakul 50000 0, 1 100000 0, 4 125000 0, 2 150000 0, 2 200000 0, 1

Döntéselmélet – Példa 2 • Egy fenyőfát 8$-ért kívánnak értékesíteni. • Készítsük el a döntési mátrixot! Tételezzük fel, hogy nincs információnk a piaci keresleti szint valószínűségéről! Hogyan döntsön: • Használjuk fel a marketing részleg által adott valószínűségekre vonatkozó információkat! Hogyan döntsön ezek birtokában? • A vállalatvezetés úgy döntött, hogy csak akkor veszi át a terület bérleti díját, ha várhatóan 100000 db-ot el tud adni a fákból. A marketing részleg által adott előrejelzés az esetek 68%-ában jelezte előre helyesen a 100000 db eladását. A részleg 50000 db keresleténél 5%-ban jelezte a 100000 db eladását, 125000 db keresleténél 12%-ban és 150000 db keresleténél 8%-ban és 200000 db keresleténél pedig 7%ban. • Mekkora valószínűséggel veszi meg a területet? Hosszú távon

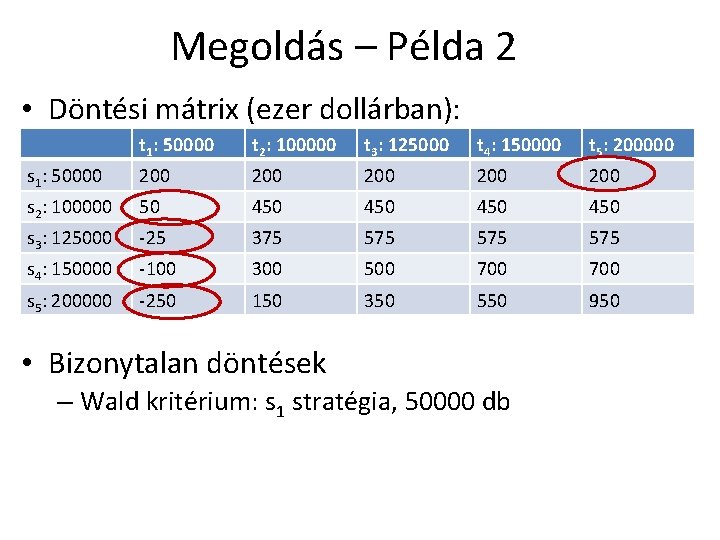
Megoldás – Példa 2 • Döntési mátrix (ezer dollárban): t 1: 50000 t 2: 100000 t 3: 125000 t 4: 150000 t 5: 200000 s 1: 50000 200 200 200 s 2: 100000 50 450 450 s 3: 125000 -25 375 575 575 s 4: 150000 -100 300 500 700 s 5: 200000 -250 150 350 550 950 • Bizonytalan döntések – Wald kritérium: s 1 stratégia, 50000 db

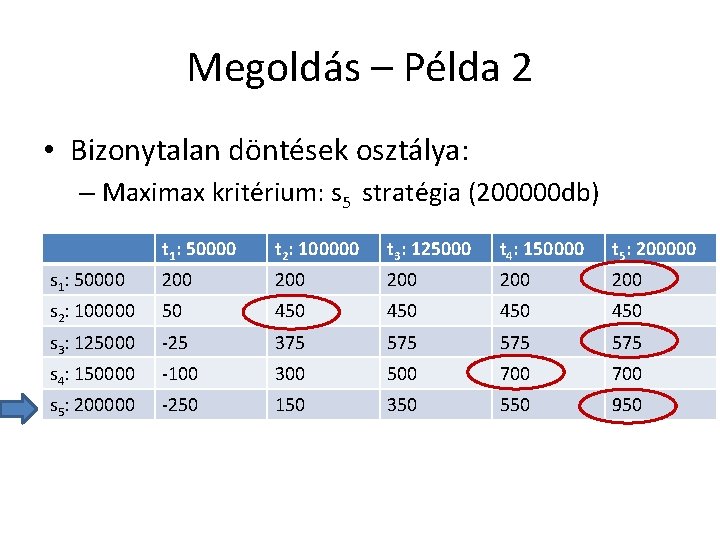
Megoldás – Példa 2 • Bizonytalan döntések osztálya: – Maximax kritérium: s 5 stratégia (200000 db) t 1: 50000 t 2: 100000 t 3: 125000 t 4: 150000 t 5: 200000 s 1: 50000 200 200 200 s 2: 100000 50 450 450 s 3: 125000 -25 375 575 575 s 4: 150000 -100 300 500 700 s 5: 200000 -250 150 350 550 950

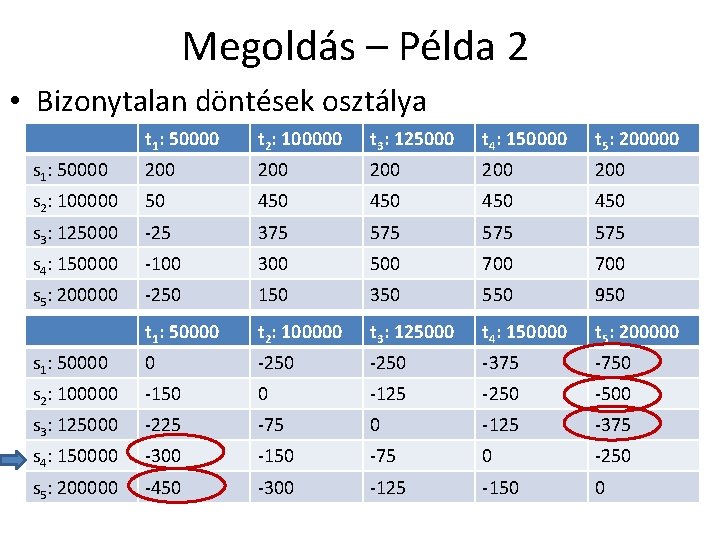
Megoldás – Példa 2 • Bizonytalan döntések osztálya t 1: 50000 t 2: 100000 t 3: 125000 – Savage kritérium: 150 000 db t 4: 150000 t 5: 200000 s 1: 50000 200 200 200 s 2: 100000 50 450 450 s 3: 125000 -25 375 575 575 s 4: 150000 -100 300 500 700 s 5: 200000 -250 150 350 550 950 t 1: 50000 t 2: 100000 t 3: 125000 t 4: 150000 t 5: 200000 s 1: 50000 0 -250 -375 -750 s 2: 100000 -150 0 -125 -250 -500 s 3: 125000 -225 -75 0 -125 -375 s 4: 150000 -300 -150 -75 0 -250 s 5: 200000 -450 -300 -125 -150 0

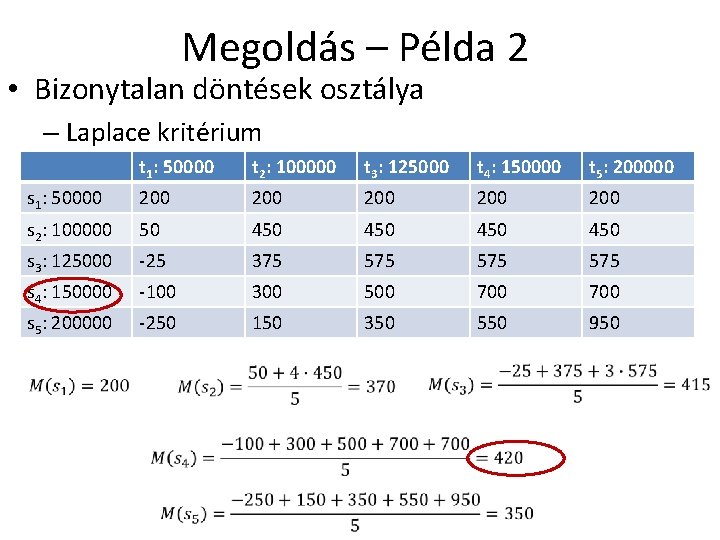
Megoldás – Példa 2 • Bizonytalan döntések osztálya – Laplace kritérium t 1: 50000 t 2: 100000 t 3: 125000 t 4: 150000 t 5: 200000 s 1: 50000 200 200 200 s 2: 100000 50 450 450 s 3: 125000 -25 375 575 575 s 4: 150000 -100 300 500 700 s 5: 200000 -250 150 350 550 950

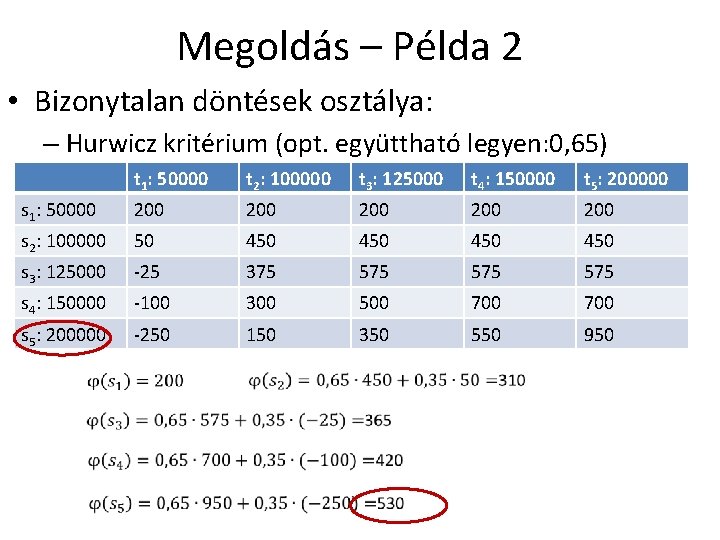
Megoldás – Példa 2 • Bizonytalan döntések osztálya: – Hurwicz kritérium (opt. együttható legyen: 0, 65) t 1: 50000 t 2: 100000 t 3: 125000 t 4: 150000 t 5: 200000 s 1: 50000 200 200 200 s 2: 100000 50 450 450 s 3: 125000 -25 375 575 575 s 4: 150000 -100 300 500 700 s 5: 200000 -250 150 350 550 950

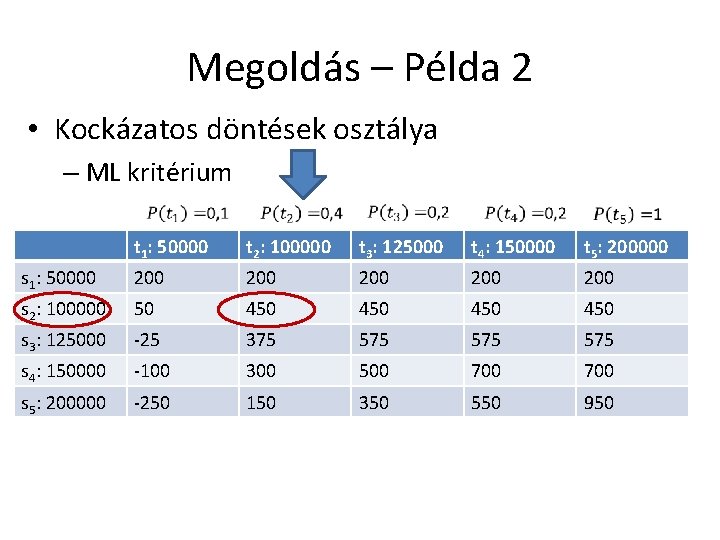
Megoldás – Példa 2 • Kockázatos döntések osztálya – ML kritérium t 1: 50000 t 2: 100000 t 3: 125000 t 4: 150000 t 5: 200000 s 1: 50000 200 200 200 s 2: 100000 50 450 450 s 3: 125000 -25 375 575 575 s 4: 150000 -100 300 500 700 s 5: 200000 -250 150 350 550 950

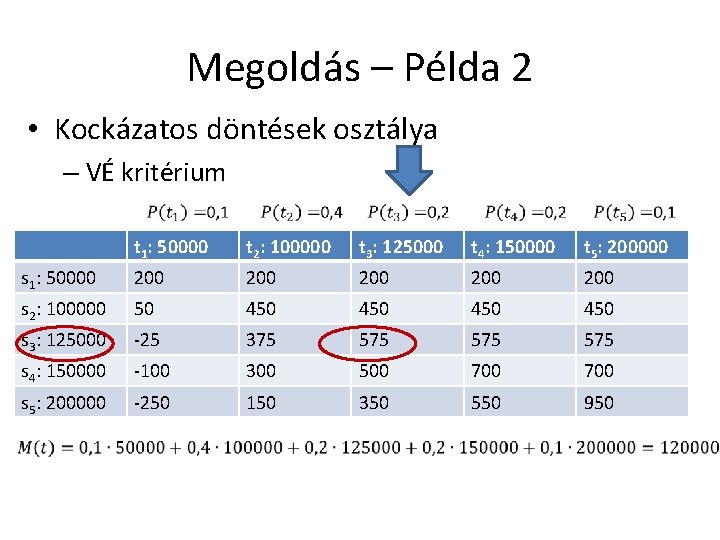
Megoldás – Példa 2 • Kockázatos döntések osztálya – VÉ kritérium t 1: 50000 t 2: 100000 t 3: 125000 t 4: 150000 t 5: 200000 s 1: 50000 200 200 200 s 2: 100000 50 450 450 s 3: 125000 -25 375 575 575 s 4: 150000 -100 300 500 700 s 5: 200000 -250 150 350 550 950

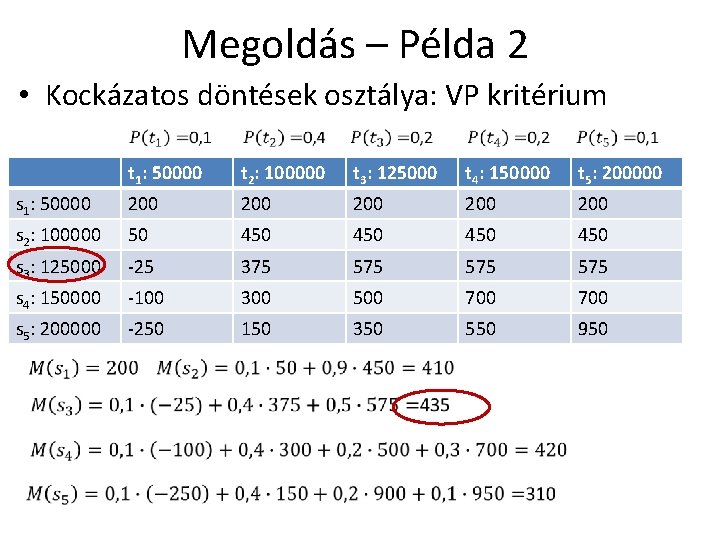
Megoldás – Példa 2 • Kockázatos döntések osztálya: VP kritérium t 1: 50000 t 2: 100000 t 3: 125000 t 4: 150000 t 5: 200000 s 1: 50000 200 200 200 s 2: 100000 50 450 450 s 3: 125000 -25 375 575 575 s 4: 150000 -100 300 500 700 s 5: 200000 -250 150 350 550 950

Megoldás – Példa 2 • Kockázatos döntés pótlólagos információk alapján Z esemény: 100000 db-ot jelez előre A priori val. Felt. val. Posteriori val. (Bayes tétel)

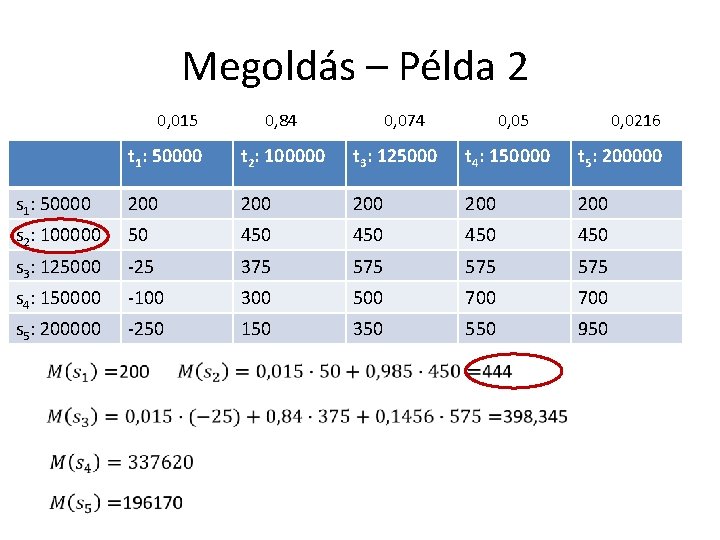
Megoldás – Példa 2 0, 015 0, 84 0, 074 0, 0216 0, 05 t 1: 50000 t 2: 100000 t 3: 125000 t 4: 150000 t 5: 200000 s 1: 50000 200 200 200 s 2: 100000 50 450 450 s 3: 125000 -25 375 575 575 s 4: 150000 -100 300 500 700 s 5: 200000 -250 150 350 550 950

Döntéselmélet – Példa 3 • A Bartlett Corporation fénycsövekkel lát el kaliforniai irodákat. Az elmúlt 20 évben komoly erőfeszítéseket tett a minőségi termékgyártás irányába, és elég nagy ügyfélkört alakított ki. A Bartlett is folyamatosan növelni szeretné a nyereségét más vállalatokhoz hasonlóan. A Bartlett beszerzési igazgatója olyan fénycsőforrásokat keres, amelyek hozzájárulnak az előbbi cél megvalósításához. Pillanatnyilag a Brightday nevű vállalattól vásárolják a fénycsöveket. E beszállító a múltbeli tapasztalati adatok alapján az alábbi hibaaránnyal dolgozik. Hibaarány Valószínűség 0, 01 0, 5 0, 02 0, 4 0, 03 0, 1 Összesen 1

Döntéselmélet – Példa 3 • A Bartlett Corporation garanciavállalása szerint a hibás fénycsöveket kicserélik, és a cserével kapcsolatos költségeket (5$/db) a vállalat állja. • A marketing osztály 100 000 db fénycső keresletét jelzi előre a következő évre. Ha mind a 100 000 db fénycsövet a Brightdaytől szerzik be, akkor a hibás fénycsövek aránya és költsége az alábbiak szerint alakul: Hibás darabok száma Költség Valószínűség Költségek várható értéke 1000 5000 0, 5 2500 2000 10000 0, 4 4000 3000 15000 0, 1 1500 1 8000 Összesen • A várható csereköltség 8000$ 100 000 db iránti kereslet esetén.

Döntéselmélet – Példa 3 • A Bartlett Corporationnél jelentkezett egy újabb beszállító, a West German. A 100 000 db fénycsőre egy 0, 25$/db alacsonyabb árajánlatot adott, mint amit a Brightday pillanatnyilag nyújt. • Bár a beszállítás költsége alacsonyabb, a Bartlettnek nincs közvetlen információja a West German hibaarányáról. Ennek becsléséhez más európai beszállítók révén szerzett tapasztalataikat használják fel. Hibaarány Valószínűség 0, 01 0, 02 0, 1 0, 04 0, 3 0, 08 0, 3 0, 10 0, 15 0, 1 Összesen 1, 0

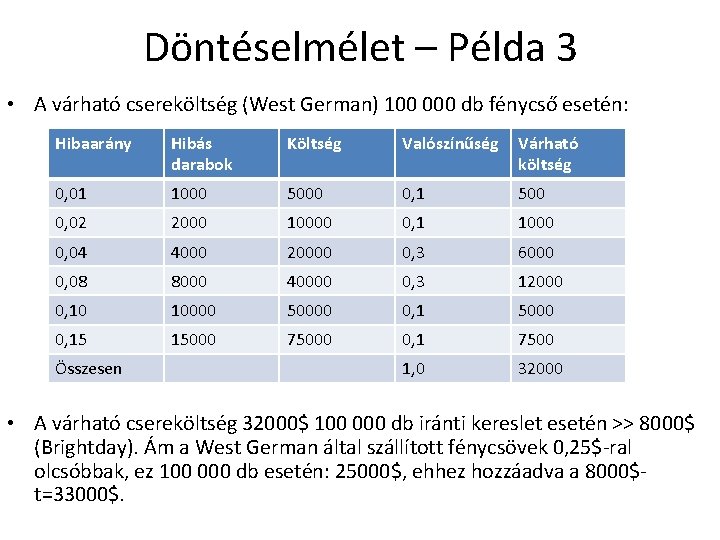
Döntéselmélet – Példa 3 • A várható csereköltség (West German) 100 000 db fénycső esetén: Hibaarány Hibás darabok Költség Valószínűség Várható költség 0, 01 1000 5000 0, 1 500 0, 02 2000 10000 0, 1 1000 0, 04 4000 20000 0, 3 6000 0, 08 8000 40000 0, 3 12000 0, 10 10000 50000 0, 1 5000 0, 15 15000 75000 0, 1 7500 1, 0 32000 Összesen • A várható csereköltség 32000$ 100 000 db iránti kereslet esetén >> 8000$ (Brightday). Ám a West German által szállított fénycsövek 0, 25$-ral olcsóbbak, ez 100 000 db esetén: 25000$, ehhez hozzáadva a 8000$t=33000$.

Döntéselmélet – Példa 3 • Eddig a várható érték kritériumot alkalmaztuk. Ha az előző számítást vesszük, akkor az a West German mellett szól. • Ugyanakkor a Bartlett a hosszú távú partnerkapcsolatok mellett érvelve fontosnak tartja a Brigthdayt, mint üzleti partnert, így további információkhoz szeretne hozzájutni. • Ezért a West Germantől mintát kér, és az így szerzett pótlólagos információkat kívánja meg kombinálni az a priori információkkal, hogy jobb döntést hozzon – ehhez a Bayes logikát használja. • A bekért 50 elemű mintában 6 darab volt hibás. Hogyan döntsön a vállalat?

Megoldás – Példa 3 • Feltételes valószínűségek meghatározása: az egyes hibaarányok, mint feltételek mellett, mekkora a valószínűsége annak, hogy egy 50 elemű mintában 6 hibásat találunk? • „A” esemény: egy 50 elemű mintában 6 a hibás, keressük: a P(A|Bi) valószínűségeket, a Bi események (hibaarányok) teljes eseményrendszert alkotnak, páronként kizárják egymást • Ezek a hibaarányok lesznek a binomiális eloszlás Hibaarány A priori Feltételes „p” értékei valószínűségek • Feltételes valószínűségek 0, 01 0, 000 (tábl) meghatározása: táblázat 0, 02 0, 1 0, 0004 vagy képlet alapján: 0, 04 0, 3 0, 0108 0, 3 0, 1063 0, 10 0, 1541 (tábl) 0, 15 0, 1419 (tábl) Összesen 1

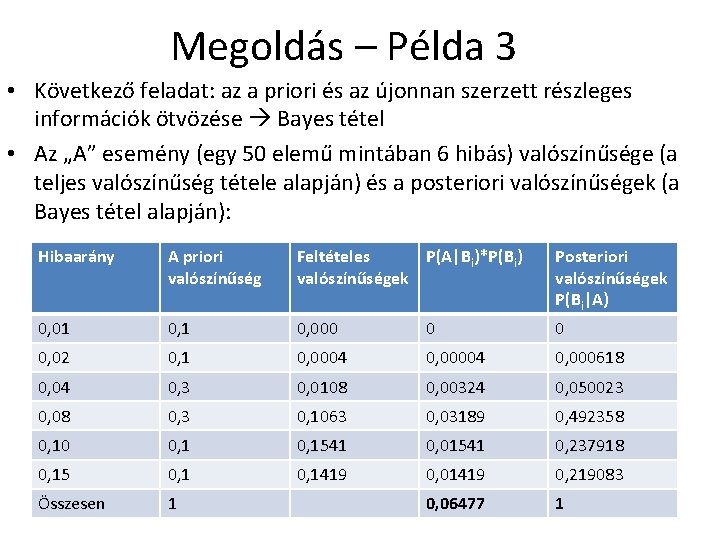
Megoldás – Példa 3 • Következő feladat: az a priori és az újonnan szerzett részleges információk ötvözése Bayes tétel • Az „A” esemény (egy 50 elemű mintában 6 hibás) valószínűsége (a teljes valószínűség tétele alapján) és a posteriori valószínűségek (a Bayes tétel alapján): Hibaarány A priori valószínűség Feltételes P(A|Bi)*P(Bi) valószínűségek Posteriori valószínűségek P(Bi|A) 0, 01 0, 000 0 0 0, 02 0, 1 0, 0004 0, 000618 0, 04 0, 3 0, 0108 0, 00324 0, 050023 0, 08 0, 3 0, 1063 0, 03189 0, 492358 0, 10 0, 1541 0, 01541 0, 237918 0, 15 0, 1419 0, 01419 0, 219083 Összesen 1 0, 06477 1

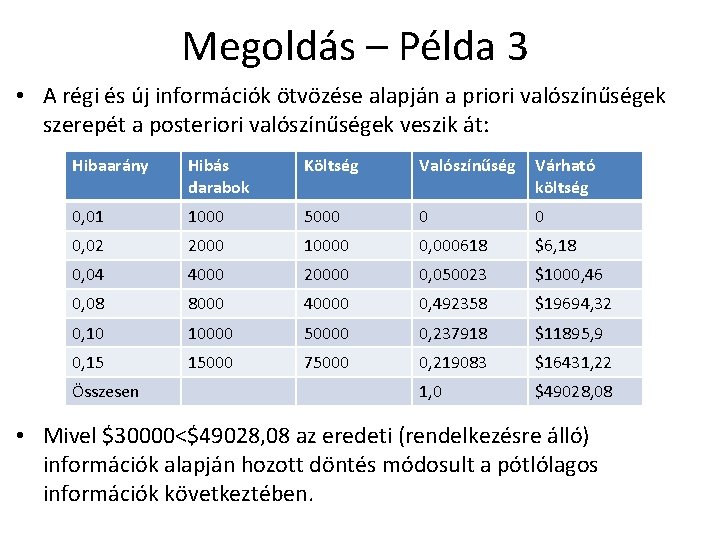
Megoldás – Példa 3 • A régi és új információk ötvözése alapján a priori valószínűségek szerepét a posteriori valószínűségek veszik át: Hibaarány Hibás darabok Költség Valószínűség Várható költség 0, 01 1000 5000 0 0 0, 02 2000 10000 0, 000618 $6, 18 0, 04 4000 20000 0, 050023 $1000, 46 0, 08 8000 40000 0, 492358 $19694, 32 0, 10 10000 50000 0, 237918 $11895, 9 0, 15 15000 75000 0, 219083 $16431, 22 1, 0 $49028, 08 Összesen • Mivel $30000<$49028, 08 az eredeti (rendelkezésre álló) információk alapján hozott döntés módosult a pótlólagos információk következtében.