KS 4 Mathematics S 9 Construction and loci

KS 4 Mathematics S 9 Construction and loci 1 of 37 © Boardworks Ltd 2005

Contents S 9 Construction and loci A S 9. 1 Constructing triangles A S 9. 2 Geometrical constructions A S 9. 3 Imagining paths and regions A S 9. 4 Loci A S 9. 5 Combining loci 2 of 37 © Boardworks Ltd 2005

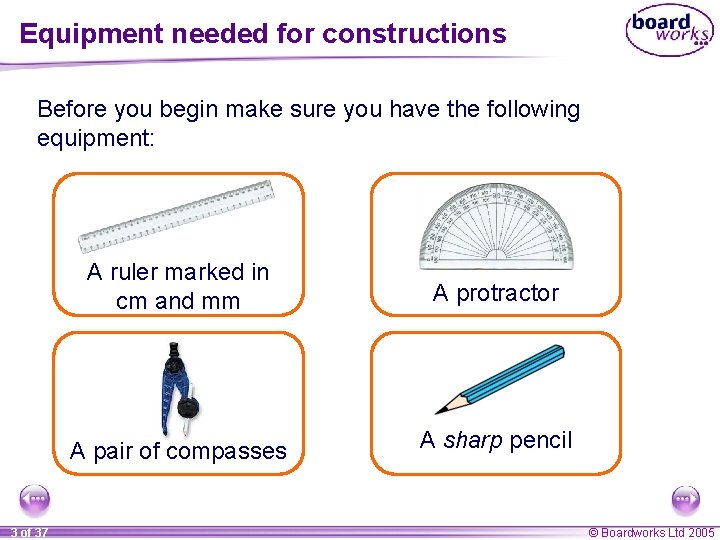
Equipment needed for constructions Before you begin make sure you have the following equipment: 3 of 37 A ruler marked in cm and mm A protractor A pair of compasses A sharp pencil © Boardworks Ltd 2005

Constructing triangles To accurately construct a triangle you need to know: The length of two sides and the included angle (SAS) The size of two angles and a side (ASA) The lengths of all three sides (SSS) or A right angle, the length of the hypotenuse and the length of one other side (RHS) 4 of 37 © Boardworks Ltd 2005

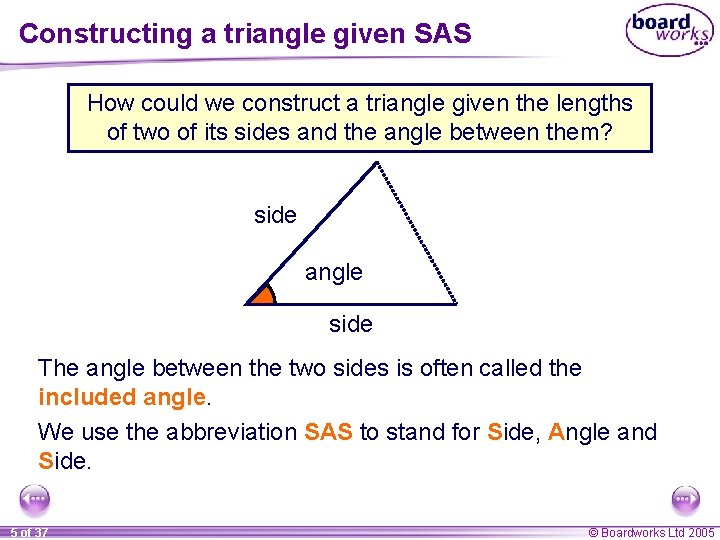
Constructing a triangle given SAS How could we construct a triangle given the lengths of two of its sides and the angle between them? side angle side The angle between the two sides is often called the included angle. We use the abbreviation SAS to stand for Side, Angle and Side. 5 of 37 © Boardworks Ltd 2005

Constructing a triangle given SAS 6 of 37 © Boardworks Ltd 2005

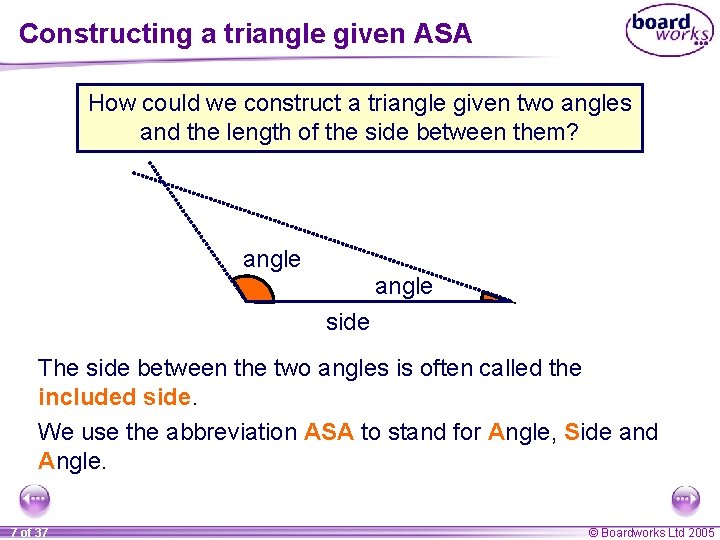
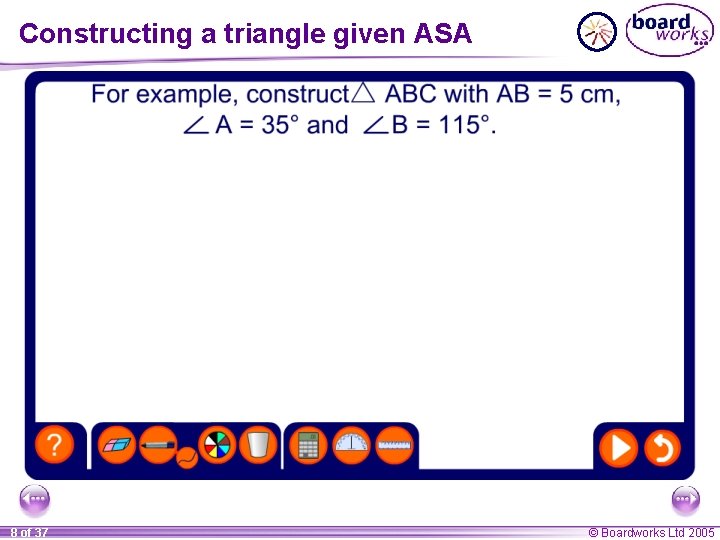
Constructing a triangle given ASA How could we construct a triangle given two angles and the length of the side between them? angle side The side between the two angles is often called the included side. We use the abbreviation ASA to stand for Angle, Side and Angle. 7 of 37 © Boardworks Ltd 2005

Constructing a triangle given ASA 8 of 37 © Boardworks Ltd 2005

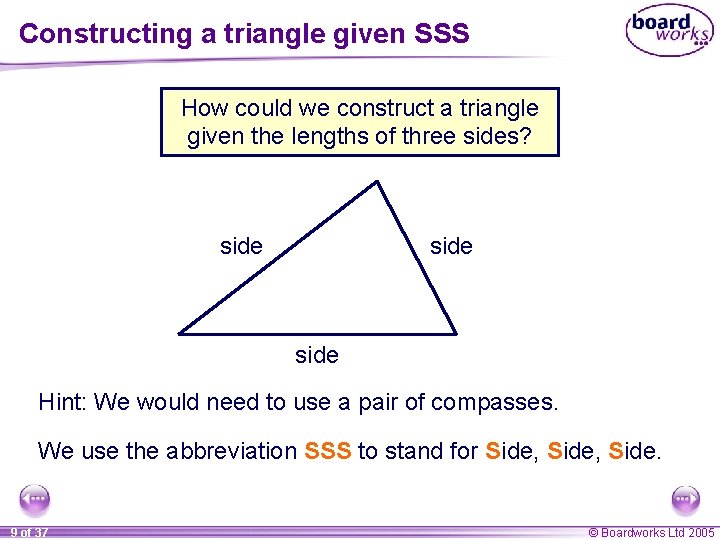
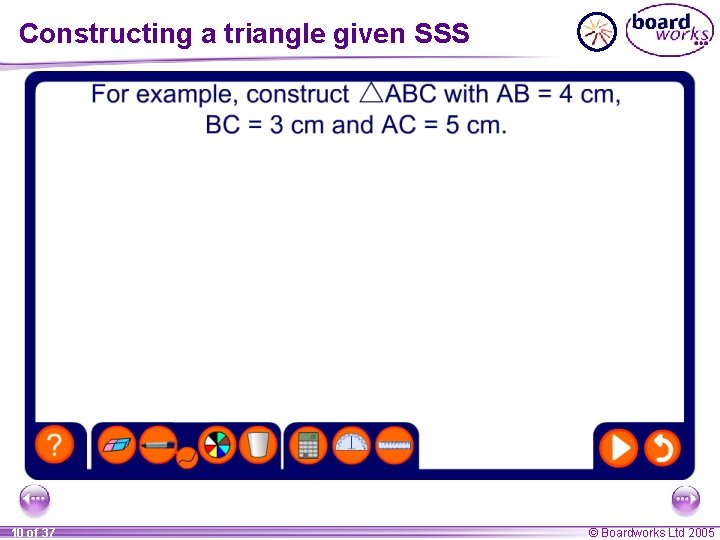
Constructing a triangle given SSS How could we construct a triangle given the lengths of three sides? side Hint: We would need to use a pair of compasses. We use the abbreviation SSS to stand for Side, Side. 9 of 37 © Boardworks Ltd 2005

Constructing a triangle given SSS 10 of 37 © Boardworks Ltd 2005

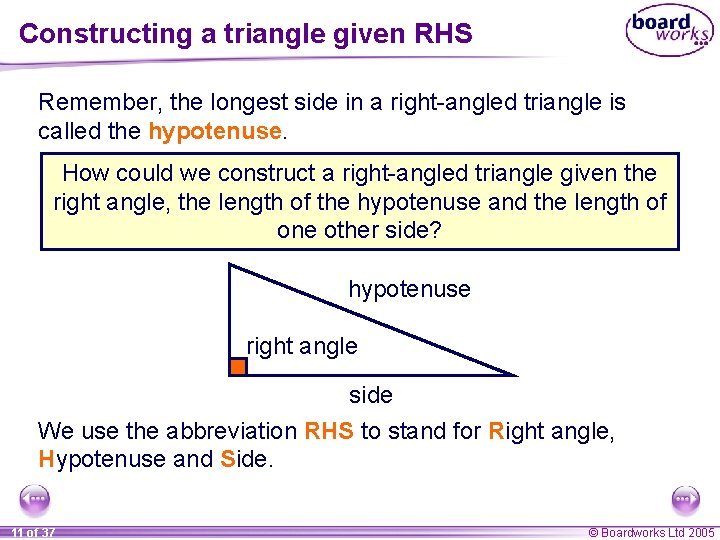
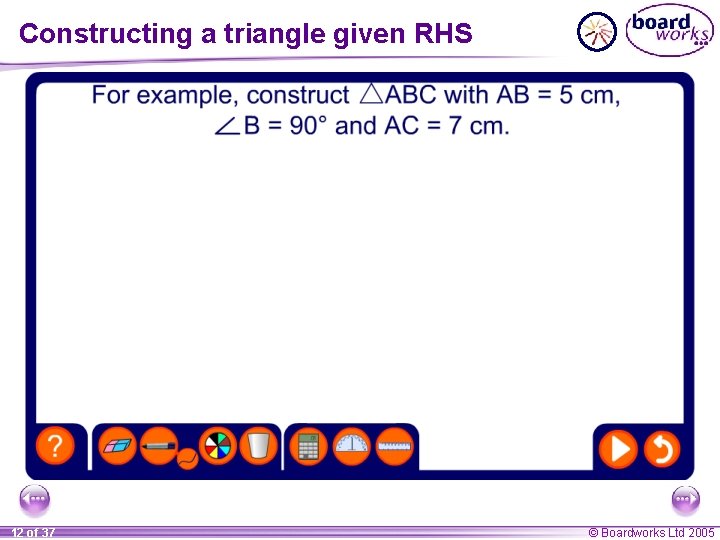
Constructing a triangle given RHS Remember, the longest side in a right-angled triangle is called the hypotenuse. How could we construct a right-angled triangle given the right angle, the length of the hypotenuse and the length of one other side? hypotenuse right angle side We use the abbreviation RHS to stand for Right angle, Hypotenuse and Side. 11 of 37 © Boardworks Ltd 2005

Constructing a triangle given RHS 12 of 37 © Boardworks Ltd 2005

Contents S 9 Construction and loci A S 9. 1 Constructing triangles A S 9. 2 Geometrical constructions A S 9. 3 Imagining paths and regions A S 9. 4 Loci A S 9. 5 Combining loci 13 of 37 © Boardworks Ltd 2005

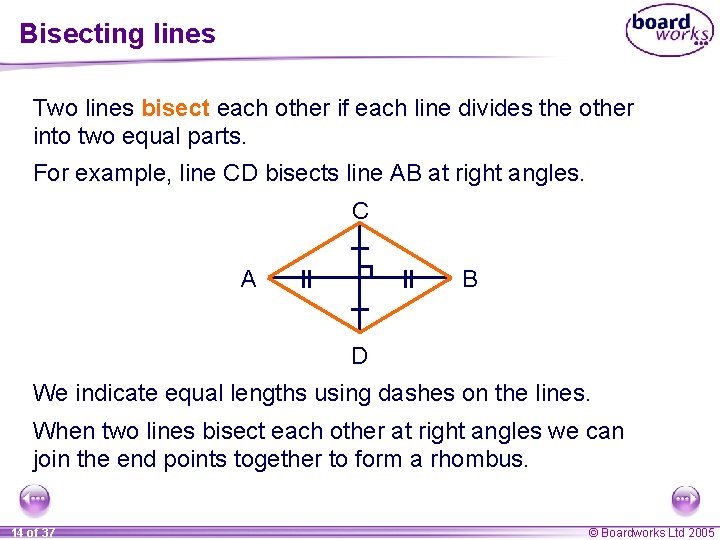
Bisecting lines Two lines bisect each other if each line divides the other into two equal parts. For example, line CD bisects line AB at right angles. C A B D We indicate equal lengths using dashes on the lines. When two lines bisect each other at right angles we can join the end points together to form a rhombus. 14 of 37 © Boardworks Ltd 2005

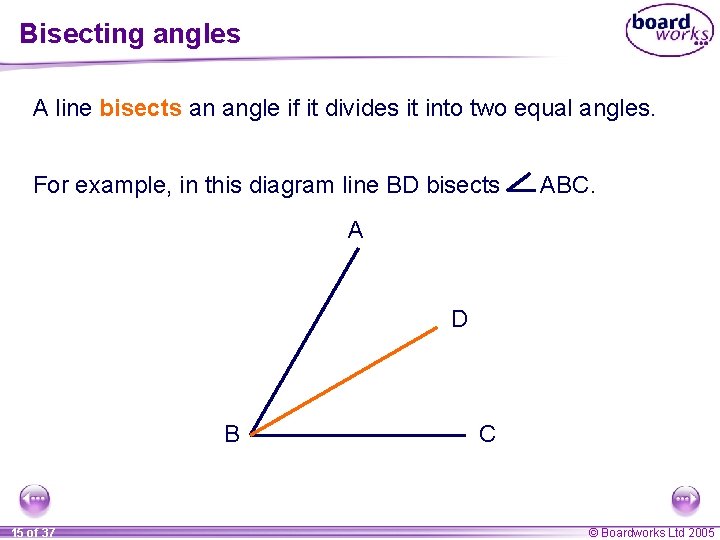
Bisecting angles A line bisects an angle if it divides it into two equal angles. For example, in this diagram line BD bisects ABC. A D B 15 of 37 C © Boardworks Ltd 2005

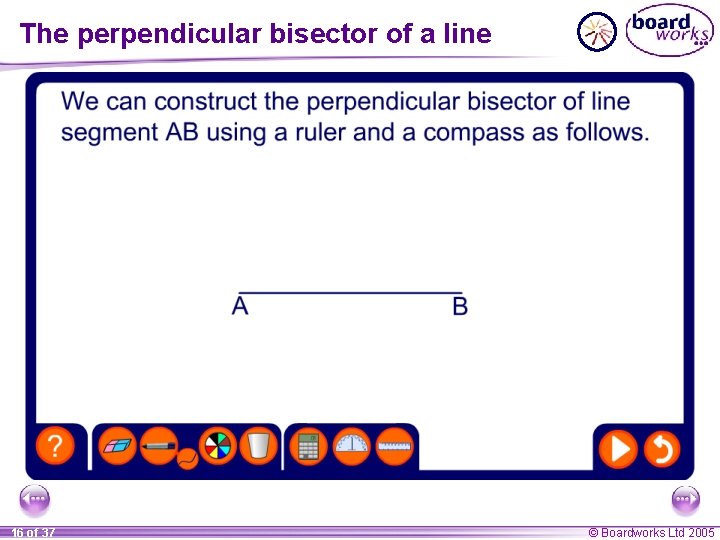
The perpendicular bisector of a line 16 of 37 © Boardworks Ltd 2005

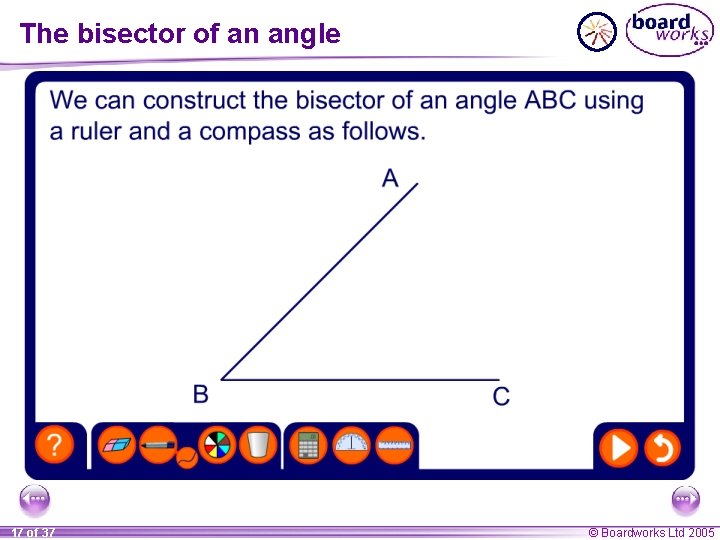
The bisector of an angle 17 of 37 © Boardworks Ltd 2005

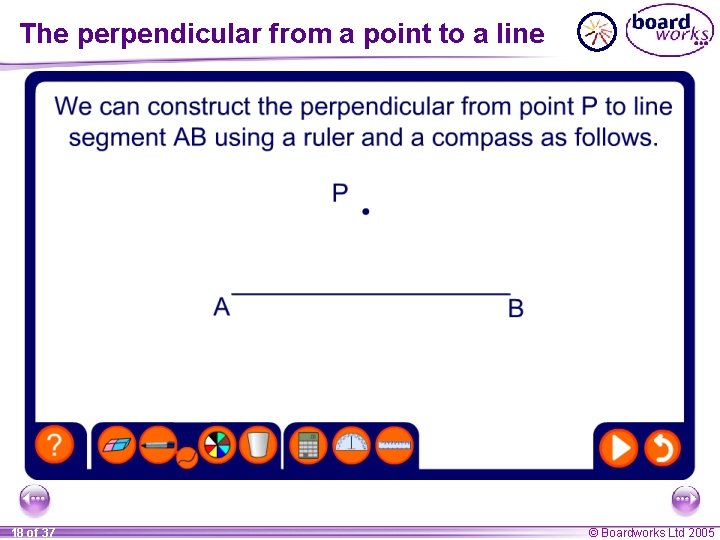
The perpendicular from a point to a line 18 of 37 © Boardworks Ltd 2005

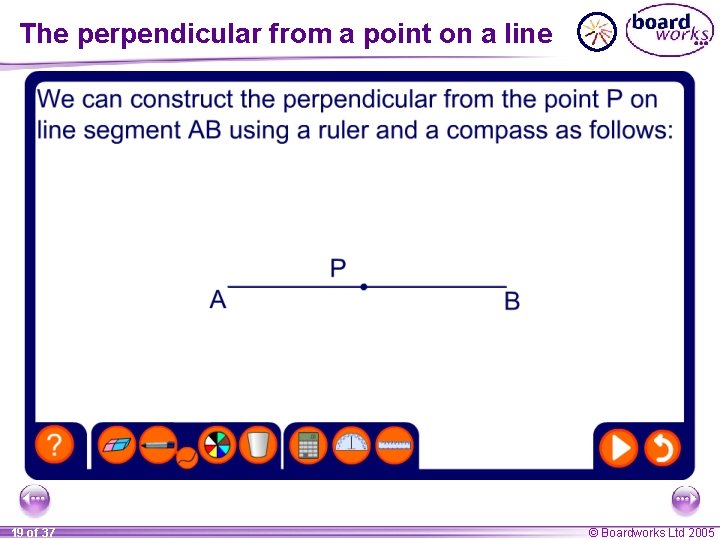
The perpendicular from a point on a line 19 of 37 © Boardworks Ltd 2005

Contents S 9 Construction and loci A S 9. 1 Constructing triangles A S 9. 2 Geometrical constructions A S 9. 3 Imagining paths and regions A S 9. 4 Loci A S 9. 5 Combining loci 20 of 37 © Boardworks Ltd 2005

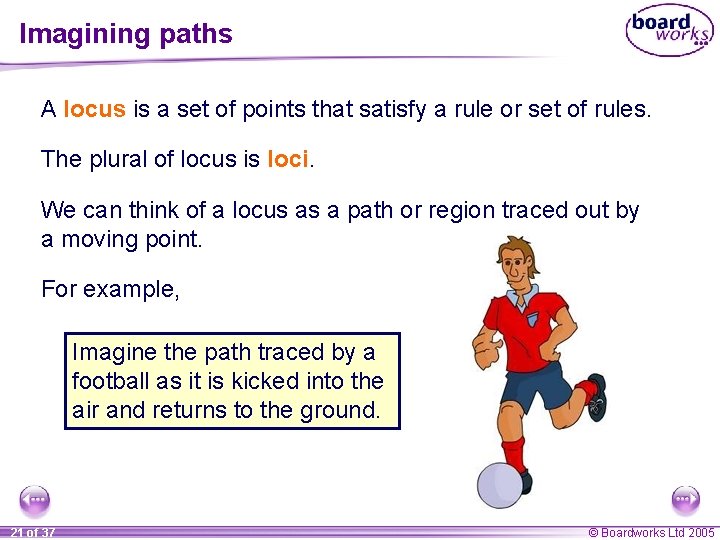
Imagining paths A locus is a set of points that satisfy a rule or set of rules. The plural of locus is loci. We can think of a locus as a path or region traced out by a moving point. For example, Imagine the path traced by a football as it is kicked into the air and returns to the ground. 21 of 37 © Boardworks Ltd 2005

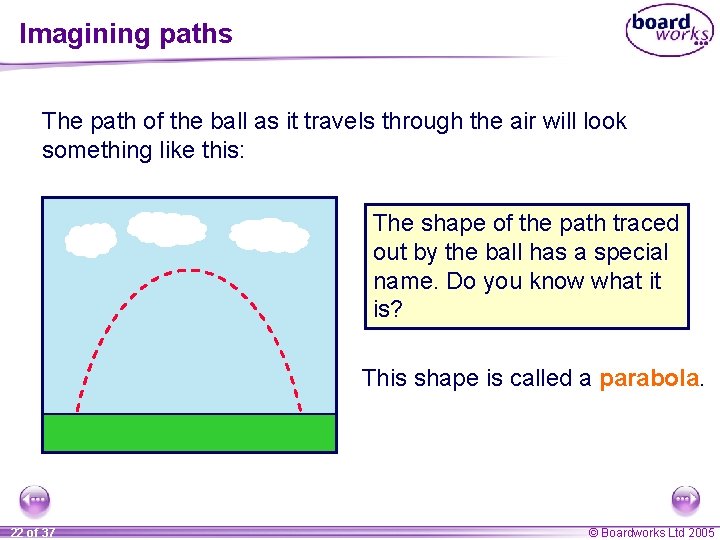
Imagining paths The path of the ball as it travels through the air will look something like this: The shape of the path traced out by the ball has a special name. Do you know what it is? This shape is called a parabola. 22 of 37 © Boardworks Ltd 2005

Imagining paths Some fluffy dice hangs from the rear-view mirror in a car and swing from side to side as the car moves forwards. Can you imagine the path traced out by one of the die? How could you represent the path in two dimensions? What about in three dimensions? 23 of 37 © Boardworks Ltd 2005

Imagining paths A nervous woman paces up and down in one of the capsules on the Millennium Eye as she ‘enjoys’ the view. Can you imagine the path traced out by the woman? How could you represent the path in two dimensions? What about in three dimensions? 24 of 37 © Boardworks Ltd 2005

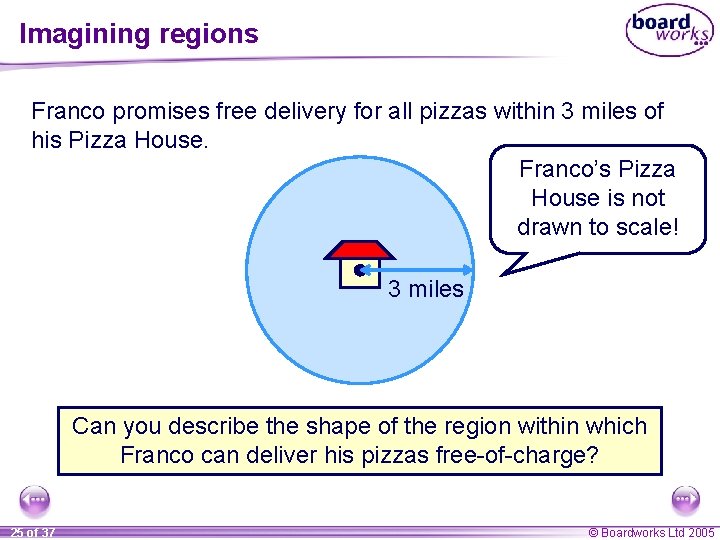
Imagining regions Franco promises free delivery for all pizzas within 3 miles of his Pizza House. Franco’s Pizza House is not drawn to scale! 3 miles Can you describe the shape of the region within which Franco can deliver his pizzas free-of-charge? 25 of 37 © Boardworks Ltd 2005

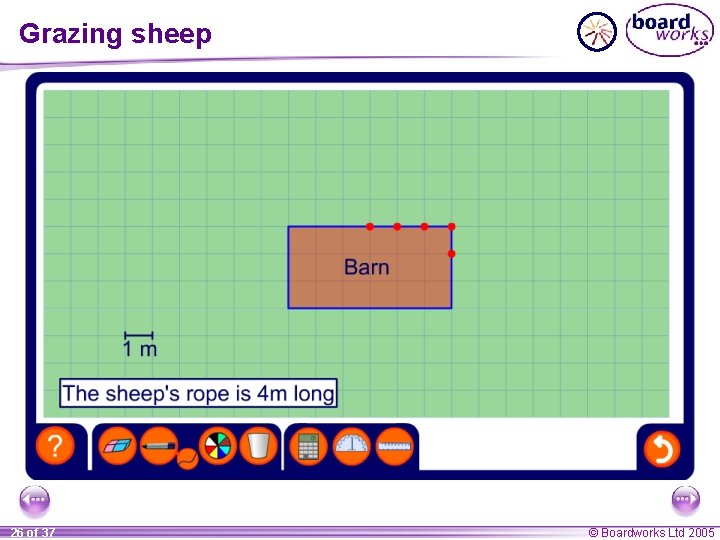
Grazing sheep 26 of 37 © Boardworks Ltd 2005

Contents S 9 Construction and loci A S 9. 1 Constructing triangles A S 9. 2 Geometrical constructions A S 9. 3 Imagining paths and regions A S 9. 4 Loci A S 9. 5 Combining loci 27 of 37 © Boardworks Ltd 2005

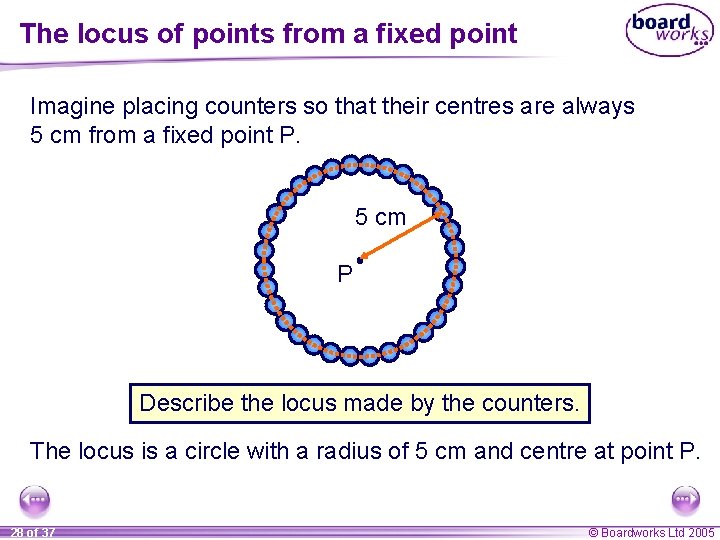
The locus of points from a fixed point Imagine placing counters so that their centres are always 5 cm from a fixed point P. 5 cm P Describe the locus made by the counters. The locus is a circle with a radius of 5 cm and centre at point P. 28 of 37 © Boardworks Ltd 2005

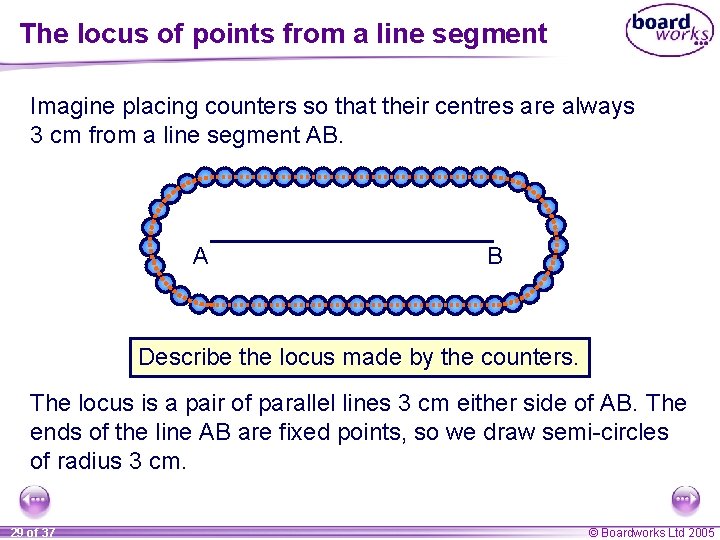
The locus of points from a line segment Imagine placing counters so that their centres are always 3 cm from a line segment AB. A B Describe the locus made by the counters. The locus is a pair of parallel lines 3 cm either side of AB. The ends of the line AB are fixed points, so we draw semi-circles of radius 3 cm. 29 of 37 © Boardworks Ltd 2005

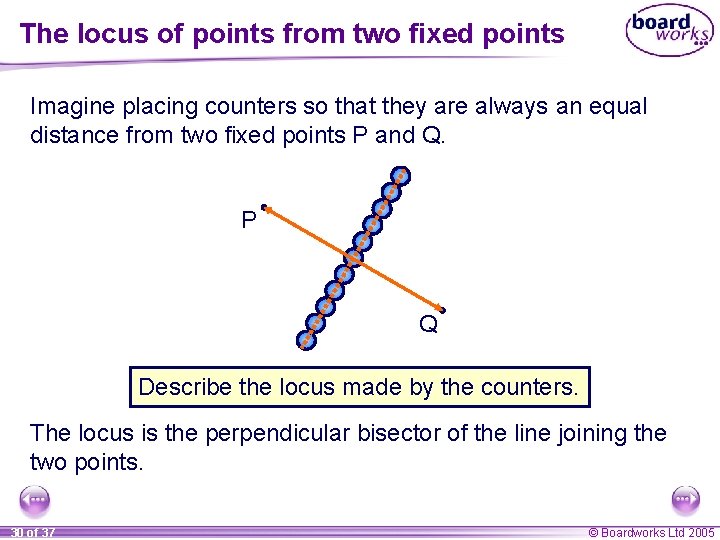
The locus of points from two fixed points Imagine placing counters so that they are always an equal distance from two fixed points P and Q. P Q Describe the locus made by the counters. The locus is the perpendicular bisector of the line joining the two points. 30 of 37 © Boardworks Ltd 2005

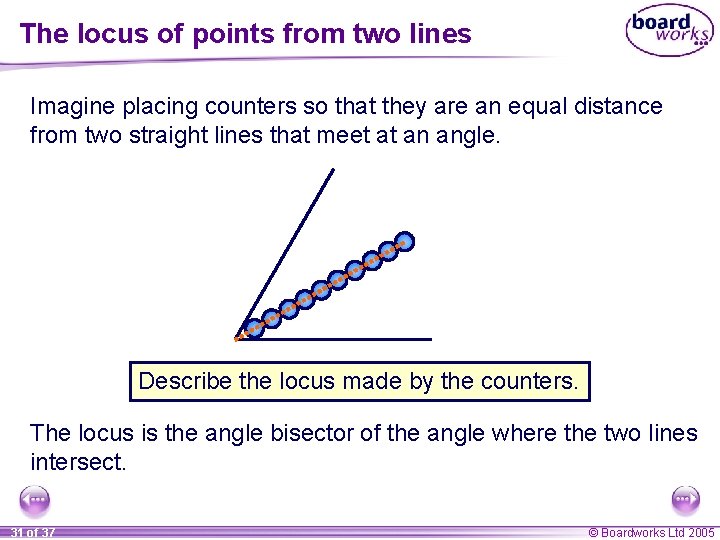
The locus of points from two lines Imagine placing counters so that they are an equal distance from two straight lines that meet at an angle. Describe the locus made by the counters. The locus is the angle bisector of the angle where the two lines intersect. 31 of 37 © Boardworks Ltd 2005

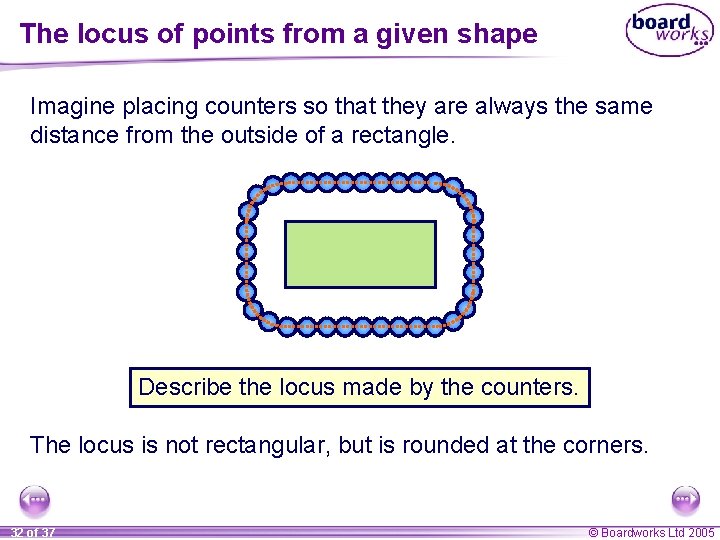
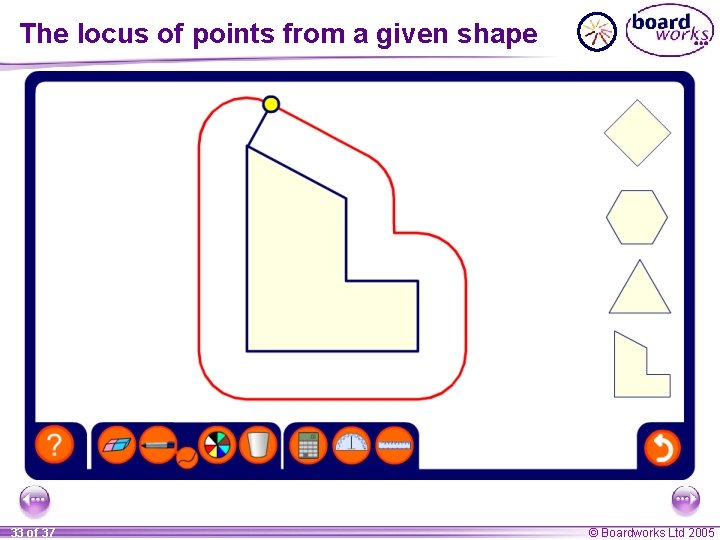
The locus of points from a given shape Imagine placing counters so that they are always the same distance from the outside of a rectangle. Describe the locus made by the counters. The locus is not rectangular, but is rounded at the corners. 32 of 37 © Boardworks Ltd 2005

The locus of points from a given shape 33 of 37 © Boardworks Ltd 2005

Contents S 9 Construction and loci A S 9. 1 Constructing triangles A S 9. 2 Geometrical constructions A S 9. 3 Imagining paths and regions A S 9. 4 Loci A S 9. 5 Combining loci 34 of 37 © Boardworks Ltd 2005

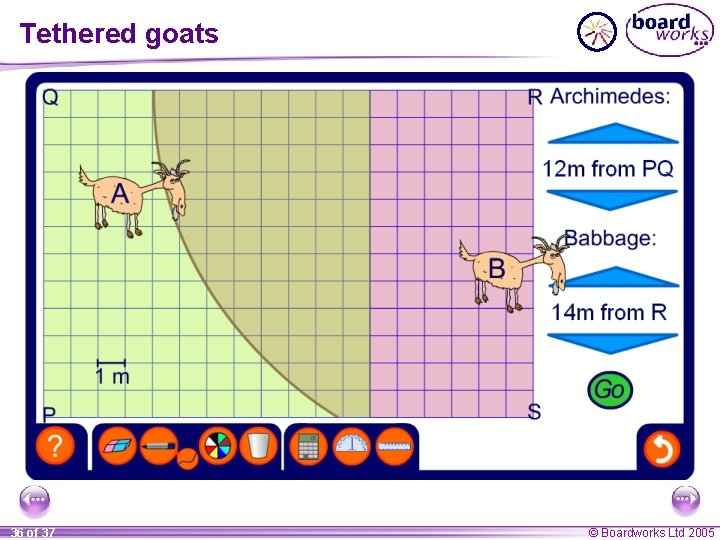
Combining loci Suppose two goats, Archimedes and Babbage, occupy a fenced rectangular area of grass of length 18 m and width 12 m. Archimedes is tethered so that he can only eat grass that is within 12 m from the fence PQ and Babbage is tethered so that he can only eat grass that is within 14 m of post R. Describe how we could find the area that both goats can graze. 35 of 37 © Boardworks Ltd 2005

Tethered goats 36 of 37 © Boardworks Ltd 2005

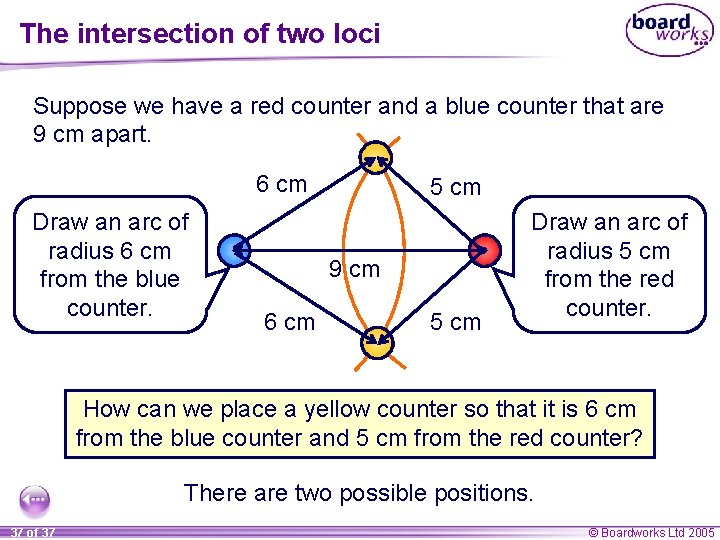
The intersection of two loci Suppose we have a red counter and a blue counter that are 9 cm apart. 6 cm Draw an arc of radius 6 cm from the blue counter. 5 cm 9 cm 6 cm 5 cm Draw an arc of radius 5 cm from the red counter. How can we place a yellow counter so that it is 6 cm from the blue counter and 5 cm from the red counter? There are two possible positions. 37 of 37 © Boardworks Ltd 2005