Knowledge Representation Welcome Artificial Intelligence DR GHASSAN ISSA

Knowledge Representation Welcome Artificial Intelligence DR. GHASSAN ISSA 2020

Knowledge Representation In order to solve problems in AI, knowledge about the problem must be represented using a knowledge representation method or approach. We need to capture information from complex real-world problems and be able to represent this information in the computer to enable the computer not just to store knowledge , but be able to reason about, learn from it, and solve problems.

Knowledge and Data Knowledge : The symbolic representation of aspects of some named universe of discourse. Facts Rules Complex relationships Data : The symbolic representation of simple aspects of some named universe of discourse. Facts simple relationship (Binary relationship)

Origins of Knowledge Deep Knowledge (First-Principle Knowledge) Heuristic Knowledge: Based on scientific theories, very detailed, found in books, requires great efforts to compile. Used primarily in explanation-based systems based on experience, easy to work with, consists of causes and effects, not necessarily accurate. Motor skill Knowledge Very difficult to capture, can be learned by actual doing and repetition. One example is how to learn to ride a bycle.

Types of Knowledge Declarative Knowledge – It includes concepts, facts, and objects and expressed in a declarative sentence. Structural Knowledge – It is a basic problem-solving knowledge that describes the relationship between concepts and objects. Procedural Knowledge – This is responsible for knowing how to do something and includes rules, strategies, procedures, etc. Meta Knowledge – Meta Knowledge defines knowledge about other types of Knowledge. Heuristic Knowledge – This represents some expert knowledge in the field or subject.

Techniques for Knowledge Representation Logical representation Semantic Networks Frames Production Rules Objects Hybrid representation

Logic A Simple type of reasoning which humans carry out involves the manipulations of propositions. Assertions about parts of the universe can be formulated precisely without ambiguity using logic. . A legal Statement in logic is called a “well-formed formula WFF”. With logic we can arrive at a Formal Deduction System where it is possible to deduce logical consequences from a given set of WFFs. There are two types of logics: classical and non-classical. Propositional logic and Predicate logic are types of classical logics. Many-valued logic, situational logic, non. Monotonic Logic, Modal Logic, Fuzzy Logic, Temporal Logic, are all examples of non-classical Logics.

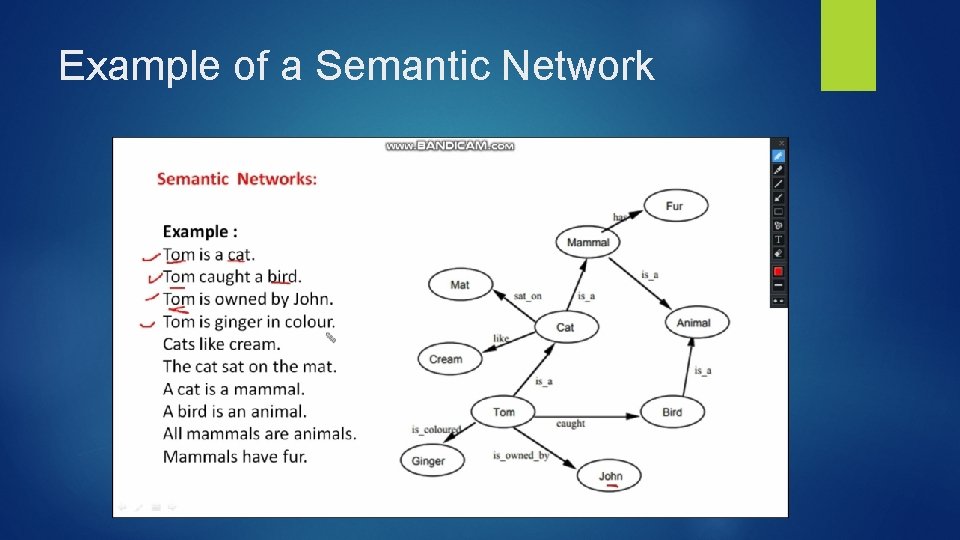
Semantic Networks Semantic networks work as an alternative of predicate logic for knowledge representation. In Semantic networks, you can represent your knowledge in the form of graphical networks. This network consists of nodes representing objects and arcs which describe the relationship between those objects. Also, it categorizes the object in different forms and links those objects. This representation consist of two types of relations: IS-A relation (Inheritance) Kind-of-relation

Example of a Semantic Network

Frames are knowledge structures, which represent prototypical constellations of element o attributes. Frames are said to contain slots, which may be used to hold several types of information. It is often described as declarative knowledge, descriptive knowledge about some object. The slots may also contain procedures (i. e. procedural knowledge or descriptions of how to do things, not descriptions of things themselves). When slots contain procedural knowledge, this is often called "procedural attachment. " This is an important distinction between frames and semantic networks. Frames can also represent procedures, so they are known as having a procedural nature as well as a declarative capability.

Rule-Based representation Called a production system. Knowledge can be represented as a series of IFTHEN rules where the first part or the antecedent of the rule is called the premise, and the second part or the consequence is termed the conclusion. When a premise is judged to be true, the rule is "triggered, " and its conclusion becomes a fact known to the rest of the production system. Premises are established: (1) By finding other rules, which have those premises as conclusions, and by then working to trigger those other rules. (2) By appeal to the user of the expert system in the form of an interactive question (3) By reference to a database of facts.

LOGIC as a Knowledge representation and reasoning system Propositional Calculus: The Propositional Calculus is a logical framework that deals with propositions as atomic units of meaning. Predicate Calculus: Unlike the propositional calculus, we can qualify a proposition in the predicate calculus with variables Non-classical Logic: deals with time, location, and uncertainty (Situational Logic, Temporal Logic, Fuzzy Logic)

First order Predicate Logic (Calculus) Syntax FIRST-ORDER PREDICATE CALCULUS First-order predicate calculus allows quantified variables to refer to objects in the domain of discourse and not to predicates or functions. A logical statement is called wff , and consists of the following : 1. Predicate Symbols {P 1, P 2, P 3, …} 2. Function Symbols {F 1, F 2, F 3, …} 3. Variable Symbols {X 1, X 2, X 3, …} 4. Constant Symbols {a 1, a 2, a 3, …} 5. Quantifiers : for all there exist Ex. x student(x) goes(x , school) x student(x) ~ goes(x , school)

6. Parenthesis [ ] , ( ) , { } 7. Connectors : and or ~ , ! not implication if and only if Note : Function return values , Predicate is description of some state (either True or False)

Equivalence Rules Idempotency: P v P ≡ P P ^ P ≡ P Commutativity: P v Q ≡ Q v P P ^ Q ≡ Q ^ P P ↔ Q ≡ Q ↔ P Associativity: [P v Q] v R ≡ P v [Q v R] [P ^ Q] ^ R ≡ P ^ [Q ^ R]

Absorption: P v [P ^ Q] ≡ P P ^ [P ^ Q] ≡ P Distributivity: P ^ [Q v R] ≡ [P ^ Q] v [P ^ R] P v [Q ^ R] ≡ [P v Q] ^ [P v R] Double negation: ¬¬P ≡ P De Morgan: ¬[P v Q] ≡ ¬P ^ ¬Q ¬[P ^ Q] ≡ ¬P v ¬Q

Tautology: P v Q ≡ P if P is a tautology. P ^ Q ≡ Q if P is a tautology. Unsatisfiability: P v Q ≡ Q if P is unsatisfiable. P ^ Q ≡ P if P is unsatisfiable. Conditional elimination: P→ Q ≡ ¬P v Q Bi-conditional elimination: P ↔ Q ≡ [P → Q] ^ [Q → P].

INTERPRETATION Let the domain D be a nonempty set. An interpretation over D is an assignment of the entities of D to each of the constant, variable, predicate, and function symbols of a predicate calculus expression, such that: 1. Each constant is assigned an element of D. 2. Each variable is assigned to a nonempty subset of D; these are the allowable substitutions for that variable. 3. Each function f of arity m is defined on m arguments of D and defines a mapping from Dm into D. 4. Each predicate p of arity n is defined on n arguments from D and defines a mapping from Dn into {T, F}. Given an interpretation, the meaning of an expression is a truth value assignment over the interpretation.

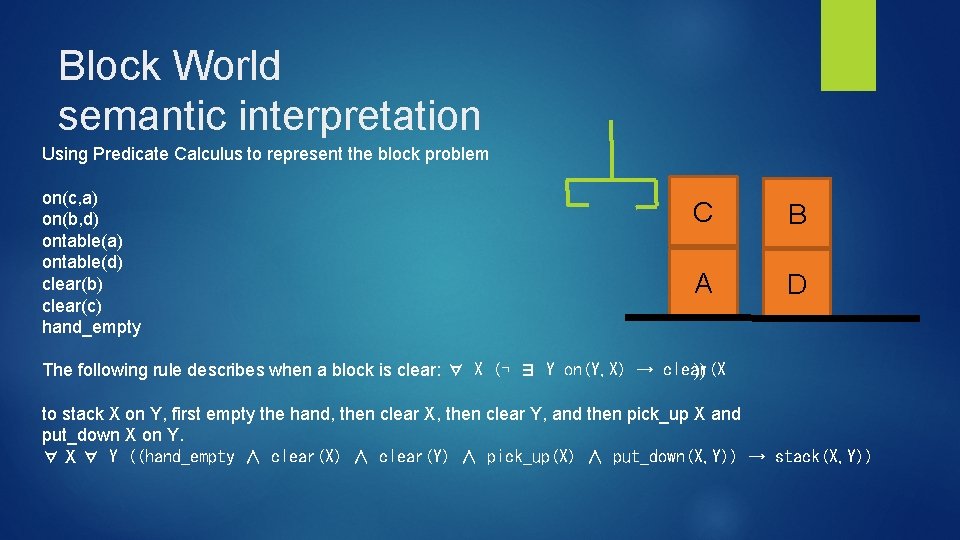
Block World semantic interpretation Using Predicate Calculus to represent the block problem on(c, a) on(b, d) ontable(a) ontable(d) clear(b) clear(c) hand_empty C B A D The following rule describes when a block is clear: ∀ X (¬ ∃ Y on(Y, X) → clear(X )) to stack X on Y, first empty the hand, then clear X, then clear Y, and then pick_up X and put_down X on Y. ∀ X ∀ Y ((hand_empty ∧ clear(X) ∧ clear(Y) ∧ pick_up(X) ∧ put_down(X, Y)) → stack(X, Y))

Logical Inferences The ability to infer new correct expressions from a set of true assertions is an important feature of the predicate calculus. These new expressions are correct in that they are consistent with all previous interpretations of the original set of expressions. An inference rule is essentially a mechanical means of producing new predicate calculus sentences from other sentences. That is, inference rules produce new sentences based on the syntactic form of given logical assertions.

Inference Rules Modus Ponens (Deduction Rule) A B (T) A (T) B (T) Abduction A B (T) A (T) Resolution A V B C V ~ B (T) A V C (T)

Soundness and Completeness When every sentence X produced by an inference rule operating on a set S of logical expressions logically follows from S, the inference rule is said to be sound. If the inference rule is able to produce every expression that logically follows from S, then it is said to be complete.

Unification, clausal form, and Resolution Conversion Of Logical Expression To Clausal Form Clause Conjunction of Disjuncts Ex. (A B) (C D) (E F v G). Clause Form : Output : Conjunction of Disjuncts

Steps 1. Eliminate “ ” using “ a b ~ a b “ 2. Reduce the scope of negation : 3. ~ (~ a) a ~ x a(x) x ~ a(x) ~ (a b) ~ a ~ b Rename quantified ( , ) variables for repeated quantifiers x a(x) x b(x) x a(x) y b(y).

4. Move all the quantifiers to the left without changing there order 5. x a(x) y b(y) x y a(x) b(y) Prenex Normal Form. Eliminate using “skolemization” proccess Skolem constant : x dog(x) dog(c) Skolem function : x y mother(x , y) x mother(x , c) x mother(x , m(x)) x y z k m(x , y , k) p(k , z) x y k m(x , y , k) p(k , w(x , y)) 6. At this point all the variables are universally quantified , so you can drop all “ ”.

7. Convert expression to a conjunction of disjuncts (move Ors to atomic level) use 8. a (b c) (a b) c a (b c) (a b) (a c) Each conjunct becomes a clause and given a number 9. : associative / distributive laws : Ex. (a b) ( c b) 1 - a b 2 - c b Rename variables that are similar in different clauses 1 - a b 2 - c b 2 - c d

Example : Convert the following expression to clause form : x (a(x) [c(x , i) y c(y , x) ] ) x e(x) Steps: 1) Eliminate using A B == ~A V B x (~ a(x) [c(x , i) y c(y , x)]) x e(x) 2) reduce the scope of ~ x (~ a(x) [c(x , i) y c(y , x)]) x e(x) 3) rename the quantifiers x (~ a(x) [c(x , i) y c(y , x)]) w e(w) 4) move quantifiers to left x y w (~ a(x) [c(x , i) c(y , x)]) e(w) 5) Eliminate y using Skolem Function x w (~ a(x) [c(x , i) c(f(x) , x))]) e(w) 6) Drop (~ a(x) [c(x , i) c(f(x) , x))]) e(w)

Q v (Y A) = (QVY) ^ (Qv. A) Results from step 6 (~ a(x) [c(x , i) c(f(x) , x))]) e(w) 7) Distribution: convert to conjunction of disjuncts [(~ a(x) c(x , i)) (~ a(x) c(f(x) , x))] e(w) [~ a(x) c(x , i) e(w)] [~ a(x) c(f(x) , x)) e(w)] 8) each Conjunct becomes a clause and given a number 1 - ~ a(x) c(x , i) e(w) 2 - ~ a(x) c(f(x) , x)) e(w) 9) rename the variables 1. ~ a(x) c(x , i) e(w) 2. ~ a(z) c(f(z) , z)) e(u)

∀x{∃y(P(x, y) → Q(y))} ∧ ∀x ¬{∃z (P(x, z))} Steps: 1. eliminate “ ” ∀x ∃y{¬P(x, y) ∨ Q(y)} ∧ ∀x {¬∃z (P(x, z)) } 2. reduce the scope of ~ ∀x ∃y{¬P(x, y) ∨ Q(y)} ∧ ∀x {∀z ¬P(x, z) } 3. rename the quantifiers ∀x ∃y{¬P(x, y) ∨ Q(y)} ∧ ∀w {∀z ¬P(w, z) } 4. Move quantifiers to left ∀x ∃y∀w∀z {¬P(x, y) ∨ Q(y) ∧ ¬P(w, z) } 5. eliminate “ y” ∀x, w, z {¬P(x, f(x)) ∨ Q(f(x)) ∧ ¬P(w, z) } 6. Drop for all ∀ ¬P(x, f(x)) ∨ Q(f(x)) ∧ ¬P(w, z)

Result from step 6: ¬P(x, f(x)) ∨ Q(f(x)) ∧ ¬P(w, z) 7. convert to conjunction of disjuncts ¬P(x, f(x)) ∨ Q(f(x)) ∧ ¬P(w, z) 8. each Conjunct becomes a clause and given a number 1)¬P(x, f(x)) ∨ Q(f(x)) 2)¬P(w, z) 9. Rename Variable 1)¬P(x, f(x)) ∨ Q(f(x)) 2)¬P(w, z)

Resolution Theorem Proving Resolution refutation proves a theorem by negating the statement to be proved and adding this negated goal to the set of axioms that are known (have been assumed) to be true. It then uses the resolution rule of inference to show that this leads to a contradiction. Resolution is a sound inference rule that, when used to produce a refutation is complete

Resolution Steps let F be a set of given statements and P is the goal to be proved 1 - Convert all statements in F to clause form. 2 - Negate P and convert result to clause form , and add it to F. 3 - Repeat until a contradiction is found , or no progress can be made or a predetermined amount of effort has been spent. a) select two causes. b) use unification and resolution rule of inference to resolve them. c) if the resolvant is the empty set then a contradiction is found (stop), else add to F. Some heuristic to select the clauses : 1) chose clauses to resolve that contain complementary literals. 2) chose clauses that are part of the goal. 3) do not repeat what you chosen. (A V C) and not (A V C)

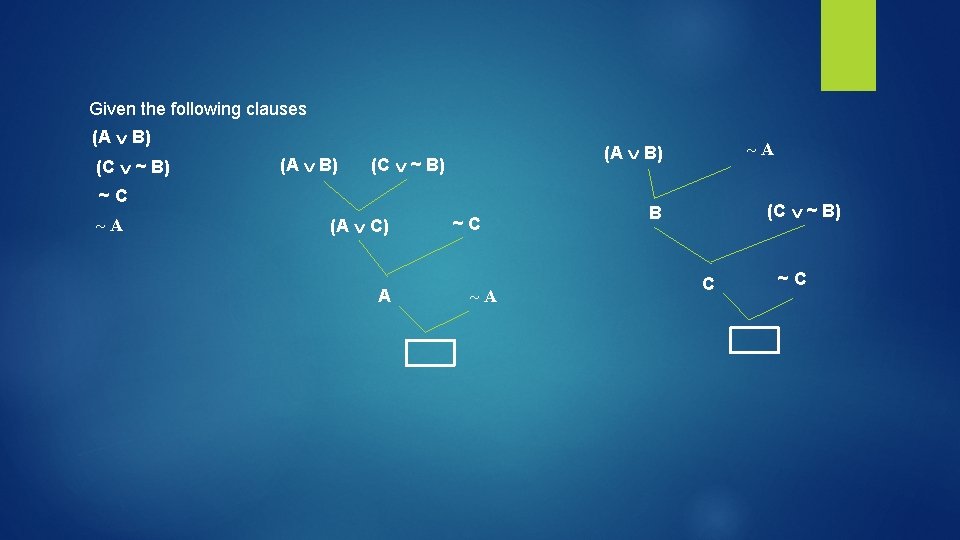
Given the following clauses (A B) (C ~ B) (A B) (C ~ B) ~ C ~A (A C) A ~A (A B) ~ C ~A (C ~ B) B C ~ C

Example : Given Fido is a dog All dogs are animals All animals will die Prove : Fido will die Fact Predicate Rule Predicate Goal Step 1: Translate English to first order predicate logic 1) dog(Fido) 2) x dog(x) animals(x) 3) x animals(x) dies(x) 4) dies(Fido) Step 2: Negate the goal ~dies(Fido)

Step 3: Convert statements to Clausal Form 1) dog(Fido) 2) ~ dog(x) animals(x) 3) ~ animals(y) dies(y) 4) ~ dies(Fido) ~ animals(y)v dies(y) {Fido / y} ~ animals(Fido) {Fido / x} ~ dog(Fido) ~ dog(x) animals(x)

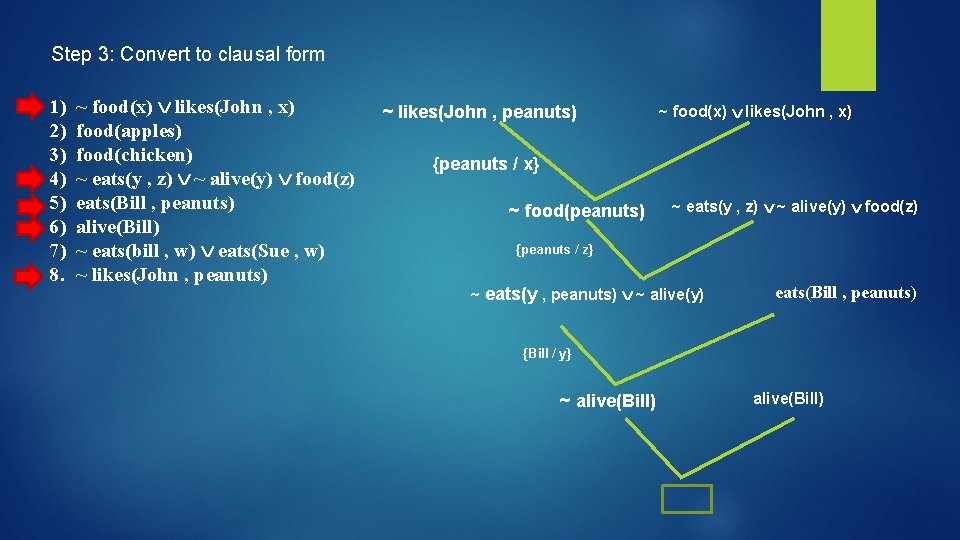
Example : Use Resolution to prove the Goal 1. 2. 3. 4. 5. 6. 7. John likes all kinds of food Predicates apples are food chicken is food any thing any one eats and isn’t killed by is food Bill eats peanuts and is still alive Sue eats everything Bill eats Both predicates have same Meaning. Choose “alive” Goal prove that John likes peanuts Step 1: Translate to Predicate Logic 1) x food(x) likes(John , x) 2) food(apples) 3) food(chicken) 4) x y eats(y , x) alive(y) food(x) 5) eats(Bill , peanuts) alive(Bill) 6) x eats(Bill , x) eats(Sue , x) 7) ~ likes(John , peanuts) For both

Step 3: Convert to clausal form 1) 2) 3) 4) 5) 6) 7) 8. ~ food(x) likes(John , x) food(apples) food(chicken) ~ eats(y , z) ~ alive(y) food(z) eats(Bill , peanuts) alive(Bill) ~ eats(bill , w) eats(Sue , w) ~ likes(John , peanuts) ~ food(x) likes(John , x) {peanuts / x} ~ food(peanuts) ~ eats(y , z) ~ alive(y) food(z) {peanuts / z} ~ eats(y , peanuts) ~ alive(y) eats(Bill , peanuts) {Bill / y} ~ alive(Bill)

Example: Any one passing history exam and winning the lottery is happy. But any one who studies or lucky can pass all his exams. John did not study but he is lucky. any one who is lucky wins the lottery. Same Predicate prove : is John happy ? Goal 1) x [pass(x , history) win(x , lottery) happy(x)] 2) x y [study(x) lucky(x) pass(x , y)] 3) ~ study(John) lucky(John) 4) x [lucky(x) win(x , lottery)] 5) ~ happy(John)

1) 2) 3) 4) 5) 6) 7) ~ pass(x , history) ~ win(x , lottery) happy(x) pass(w , y) ~ study(w) ~ pass(x , history) ~ win(x , lottery) happy(x) ~ happy(John) pass(m , r) ~ lucky(m) ~ study(John) {John / x} lucky(John) ~ lucky(p) win(p , lottery) ~ pass(John , history) ~ win(John , lottery) ~ happy(John) {John / p} ~ pass(John , history) ~ lucky(John) ~ pass(John , history) {John / m , history / r} lucky(John) pass(m , r) ~ lucky(m) ~ lucky(John)