Jednofaktorov ANOVA Jednofaktorov analza rozptylu Test o shod

Jednofaktorová ANOVA Jednofaktorová analýza rozptylu (Test o shodě více než dvou středních hodnot)

Motivační příklady • Porovnání výsledků přijímacího řízení u absolventů různých typů středních škol (gymnázium, SPŠ, SOU) • Srovnání obsahu dusíku u 5 -ti příbuzných druhů rostlin • Srovnání platů podle bydliště respondentů (krajů) …

Proč nepoužívat řadu dvouvýběrových t-testů? Skupina III • Porovnáváme-li k tříd (skupin), provádíme testů. V každém z nich je pravděpodobnost chyby prvního druhu α. • Pravděpodobnost, že uděláme alespoň jednu chybu prvního druhu pak roste s počtem porovnávaných tříd.

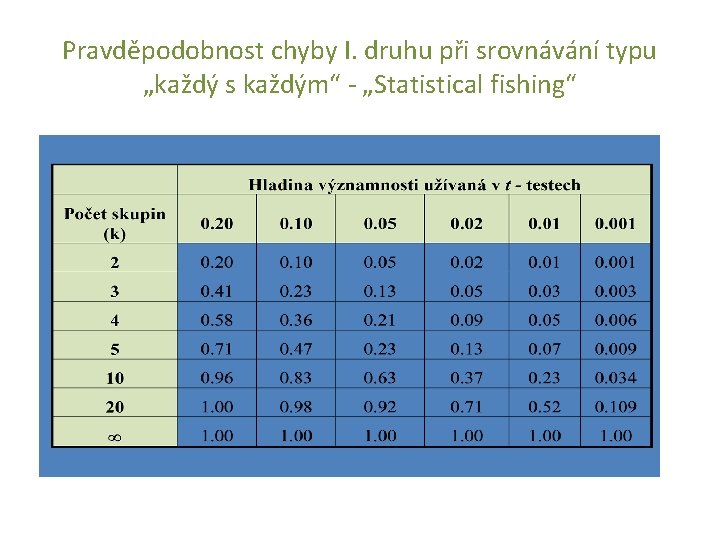
Pravděpodobnost chyby I. druhu při srovnávání typu „každý s každým“ - „Statistical fishing“

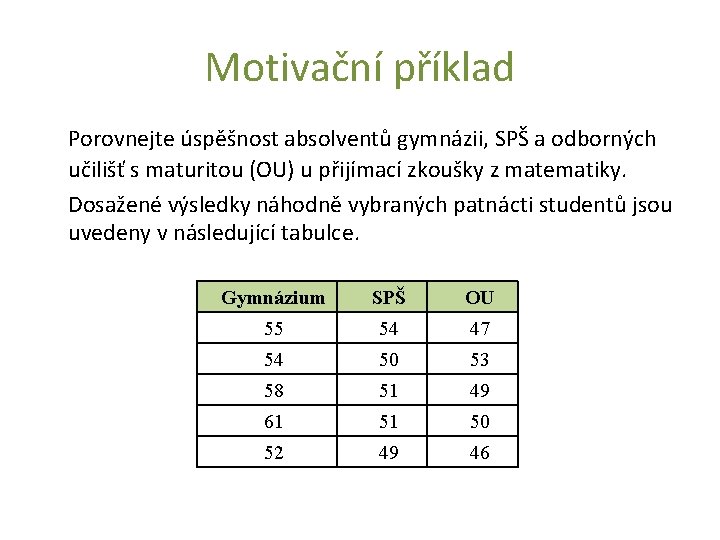
Motivační příklad Porovnejte úspěšnost absolventů gymnázii, SPŠ a odborných učilišť s maturitou (OU) u přijímací zkoušky z matematiky. Dosažené výsledky náhodně vybraných patnácti studentů jsou uvedeny v následující tabulce. Gymnázium SPŠ OU 55 54 47 54 50 53 58 51 49 61 51 50 52 49 46

Co je příčinou rozdílných výsledků? Vliv sledovaného faktoru tj. rozdíly mezi kvalitou výuky na jednotlivých typech středních škol. Reziduální (zbytkové) vlivy tj. rozdíly mezi školami v rámci tříd (není gymnázium jako gymnázium), rozdíly mezi pedagogy v rámci jedné školy, rozdíly mezi schopnostmi jednotlivých studentů, …

Jak se projevují tyto dva typy vlivů? Vliv sledovaného faktoru se projevuje rozdíly mezi třídami Reziduální (zbytkové) vlivy se projevují rozdíly uvnitř tříd

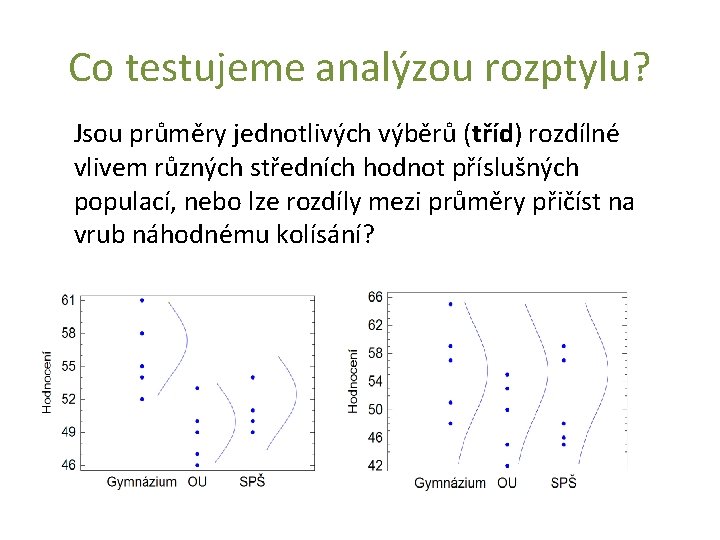
Co testujeme analýzou rozptylu? Jsou průměry jednotlivých výběrů (tříd) rozdílné vlivem různých středních hodnot příslušných populací, nebo lze rozdíly mezi průměry přičíst na vrub náhodnému kolísání?

Jak kvantifikovat tyto rozdíly? Rozdíly mezi třídami (vliv faktoru) kvantifikuje mezitřídní variabilita (součet čtverců mezi třídami) : Rozdíly uvnitř tříd (reziduální vlivy) kvantifikuje vnitřní variabilita (součet čtverců uvnitř tříd):

Celková variabilita SSTOTAL Celková variabilita (celkový součet čtverců) je definována jako součet mezitřídní variability a vnitřní variability.

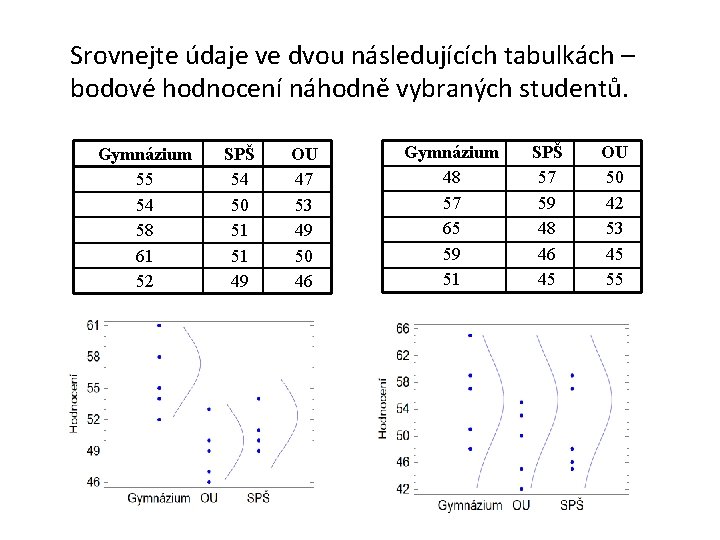
Srovnejte údaje ve dvou následujících tabulkách – bodové hodnocení náhodně vybraných studentů. Gymnázium 55 54 58 61 52 SPŠ 54 50 51 51 49 OU 47 53 49 50 46 Gymnázium 48 57 65 59 51 SPŠ 57 59 48 46 45 OU 50 42 53 45 55

Ukázka výpočtu mezitřídní a vnitřní variability

Rice Virtual Lab in Statistics autor: David Lane Applet – One Way Anova Úkol Všimněte si změn poměru mezitřídní a vnitrotřídní variability při zachování průměrů a proměnném výb. rozptylu.

ANOVA Je možné, že výběry reprezentovány takto rozdílnými průměry pocházejí ze stejného rozdělení? H 0: HA: Předpoklad: normalita výběrů, (homoskedasticita)

Odhad společného rozptylu σ2 za předpokladu platnosti H 0 Odhad na základě mezitřídní variability (rozptyl mezi třídami, průměrný mezitřídní součet čtverců, vysvětlený rozptyl) Odhad na základě vnitřní variability (rozptyl uvnitř tříd, průměrný součet čtverců uvnitř tříd, nevysvětlený rozptyl)

F-ratio (F-poměr) Poměr dvou odhadů rozptylu (na základě výběrů z normálního rozdělení) má Fisher-Snedecorovo rozdělení. Platí-li H 0: MSB je srovnatelné s MSW, F-poměr se pohybuje kolem 1. Platí-li HA: MSB je mnohem větší než MSW, F-poměr je mnohem větší než 1.

ANOVA - shrnutí Formulace H 0 a HA: H 0: H A: Testová statistika:

ANOVA - shrnutí Předpoklady testu: • Normalita (výběry pocházejí z populací s normálním rozdělením) • Homoskedasticita (shoda rozptylů – výběry pocházejí z populací se shodným rozptylem) Výpočet p-value:

Tabulka ANOVA je typickým způsobem prezentace výsledku ANOVy.

Síla testu • Zvyšuje se se zvětšující se odchylkou od H 0 (to nelze ovlivnit) • Zvyšuje se s počtem pozorování ve třídách • Zvyšuje se s vyvážeností tříd • Klesá s rostoucím počtem tříd

Post Hoc analýza (vícenásobné porovnávání) • Vysoký F-poměr indikuje existenci významných změn mezi populačními výběrovými průměry a vede k zamítnutí H 0. • V tomto případě je nutné identifikovat, které z populací signalizují významnou odchylku průměru. • LSD metoda, Duncanův test, Tukeyův test pro významné rozdíly, Scheffého test a Bonferoniho test • POZOR!!! Použijeme-li post hoc analýzu neoprávněně (v případě nezamítnuti H 0), můžeme získat informaci o falešně významných rozdílech mezi průměry.

Příklady Litschmannová M. , Statistika I. – cvičení, ANOVA – 13. 1, 13. 2

Jak postupovat při nesplnění předpokladů? Porušení homoskedasticity: Pokusíme se stabilizovat rozptyl pomocí transformací proměnných (není obsahem Statistiky I. ). Pokud se nám rozptyl stabilizovat nepodaří, nemůžeme vliv faktoru testovat. Porušení normality: Pokud je splněna podmínka homoskedasticity, můžeme použít neparametrickou obdobu ANOVy – Kruskall – Wallisův test (vícevýběrový test o shodě mediánů)

Kruskall – Wallisův test Formulace H 0 a HA: H 0 : HA: neplatí H 0 Volba testového kritéria: ( , Ti jsou součty pořadí pro jednotlivé výběry)

Kruskall – Wallisův test Předpoklad testu: Homoskedasticita Výpočet p-value:

Příklad výpočtu pozorované hodnoty a p-value při Kruskall-Wallisově testu I 67 22 10 55 94 -17 37 28 II 20 -13 11 5 38 53 5 Výběr III 106 127 13 79 37 31 22 70 76 55 91 25 Výběr IV 13 49 97 85 46 31 37 61 10 1 Rozsah výběru ni Součty pořadí Ti I 28 12, 5 6, 5 25, 5 34 1 19 15 II 11 2 8 4, 5 21 24 4, 5 8 145 20022, 3 2502, 8 7 75 5625, 0 803, 6 III 36 37 9, 5 31 19 16, 5 12, 5 29 30 25, 5 33 14 12 293 85849, 0 7154, 1 IV 9, 5 23 35 32 22 16, 5 19 27 6, 5 3 10 193, 5 37442, 3 3744, 2

Příklady Litschmannová M. , Statistika I. – cvičení, ANOVA – 13. 3