Introduction to the Theory of Computation John Paxton

Introduction to the Theory of Computation John Paxton Montana State University Summer 2003

Humor • A foreign visitor was being given a tour of Washington, D. C. one day by an American friend of hers. She was amazed at the size of the Monuments, the Congressional Buildings, and so forth. Finally she gazed upon the White House itself. "My, that's an incredibly large building!" she remarked. "Yes, it's pretty big, alright. " said her friend. "Big? It's huge!! About how many people work in there? " she asked. "Oh. . . about half. "

Chapter 2: Context-Free Languages • Applications: Capture most human language syntax, programming language syntax, the parser in a compiler • More powerful model of computation

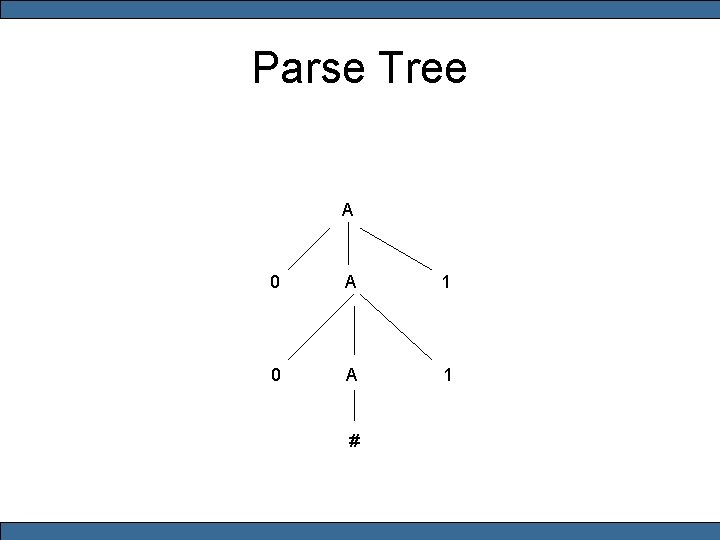
2. 1 Context-Free Grammars • A grammar consists of – – production rules variables terminals a starting variable A => 0 A 1 | #

Derivation • A => 0 A 1 => 00 A 11 => 00#11

Parse Tree A 0 A 1 #

Natural Language • <sentence> => <noun phrase> <verb phrase> • <noun phrase> => <noun> | <determiner> <noun> • <verb phrase> => <verb> • <det> => a | the • <noun> => boy | girl • <verb> => runs | plays

Context Free Grammar Definition A CFG is a 4 -tuple (V, S, R, S) where 1. V is a finite set called the variables 2. S is a finite set, disjoint from V, called the terminals 3. R is a finite set of rules, with each rule being a variable and a string of variables and terminals 4. S is the start symbol

Exercise • Identify (V, S, R, S) for A => 0 A 1 | # • Describe the language

More Definitions • u. Av yields uwv if A => w is a rule • u. Av =>* uwv if a sequence of 1 or more steps exist such that A => w • The language of the grammer is { w S* | S =>* w }

Another Grammar • <expr> => <expr> + <term> | <term> • <term> => <term> x <factor> | <factor> • <factor> => ( <expr> ) | a • Exercise: Parse tree for a + a x a • Exercise: Parse tree for (a + a) x a

Exercises • Design a context free grammar for the language {0 n 1 n | n >= 0} U {1 n 0 n | n >= 0} • Design a context free grammar for the below NFA 0 1 e

Exercises • Give a CFG that generates the language {w | w contains at least three 1 s} over the alphabet {0, 1}. • Repeat the above question for {w | w contains more 1 s than 0 s} • Repeat the above question for {w | w contains twice as many a’s as b’s} over the alphabet {a, b}

Ambiguity • <expr> => <expr> + <expr> | <expr> x <expr> | a • A string w is derived ambiguously in a CFG if it has two or more different leftmost derivations. A CFG is ambiguous if it generates some string ambiguously. • Exercise: Show a + a x a is ambiguous.

Chomsky Normal Form All rules are in one of the following forms: 1. S => e is allowed (S is the start symbol) 2. A => B C (B and C aren’t S) 3. A => a

Theorem • Any context-free language is generated by a context-free grammar in Chomsky normal form.

Proof • • Add new start symbol S 0 Add S 0 => S Eliminate an e rule, adjust other rules. Repeat above step until all e rules eliminated except for possible S 0 => e Example: A => e, B => a. Aa becomes B => a. Aa | aa. Aa | a. Aaa

Proof • Remove a unit rule A => B. Example: A => B, C => AA becomes C => BB • Repeat until all unit rules removed.

Proof • Convert all remaining rules into proper form. Example: A => a. Bc. D becomes A => U 1 U 2 U 1 => a U 2 => BU 3 => U 4 D U 4 => c

Example • S => ASA | b | e • A => a • S 0 => S • S => ASA | b | e • A => a (add new start rule)

Example • S 0 => S | e • S => AA | ASA | b • A => a (eliminate S => e) • S 0 => AA | ASA | b | e (eliminate S 0 => S) • S => AA | ASA | b • A => a

Example • • S 0 => AA | AU 1 | b | e (change S 0 => ASA) S => AA | AU 1 | b (change S => ASA) A => a U 1 => SA

Exercise • Convert the following grammar to Chomsky Normal Form: • A => BAB | e • B -> 00 | e