Introduction to the Theory of Computation John Paxton

Introduction to the Theory of Computation John Paxton Montana State University Summer 2003

Humor • A man walks up to the Marine guard at the White House front gate and asked to see President Clinton. The guard says "Sorry sir but Clinton is no longer president. " The man comes back the next day and again approaches the same guard and asks to see President Clinton. Again the guard says "Sir, Clinton is no longer president. " The man leaves but comes back the third day and again asked to see President Clinton. The guard says "Sir. . . you have been here three days in a row asking to see President Clinton. . . and I have told you each time that Clinton is no longer president. . . what gives? " The man says "I know. . . I just like hearing it. "

1. 3 Regular Expression • Pattern Recogniton – Unix (GREP) – Perl – Text Editors

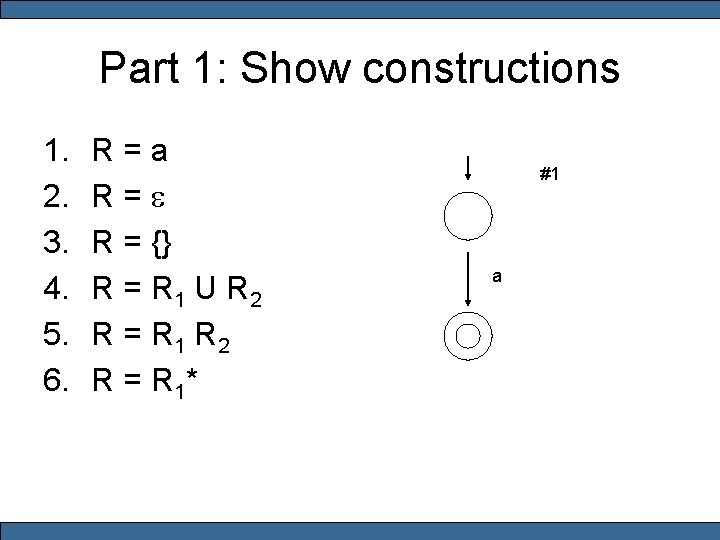
Formal Definition R is a regular expression if R is 1. a for some a in the alphabet S 2. e 3. {} 4. (R 1 U R 2) where R 1 and R 2 are both regular expressions 5. (R 1 R 2) 6. (R 1*)

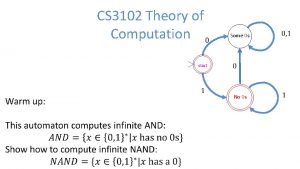
Exercise: Describe the Language • • 0*10* S*1 S* (SS)* 01 U 10 (0 U e)1* 0 S*0 U 1 S*1 U 0 U 1 1*{} {}*

Exercise: Give the Regular Expression • {w | w begins with a 1 and ends with a 0} • {w | w contains at least 3 0 s} • {w | w starts with a 0 and has odd length or starts with a 1 and has even length} • {w | the length of w is at most 5} • {w | w contains at least two 0 s and at most one 1} • All strings except the empty string

Theorem • A language is regular if and only if some regular expression describes it. • Part I. If a language is described by a regular expression, then it is regular. • Part II. If a language is regular, then it is described by a regular expression.

Part 1: Show constructions 1. 2. 3. 4. 5. 6. R = a R = e R = {} R = R 1 U R 2 R = R 1* #1 a

Exercises • Build an NFA from the regular expression (ab U a)*. • Build an NFA from the regular expression (0 U 1)*000(0 U 1)*.

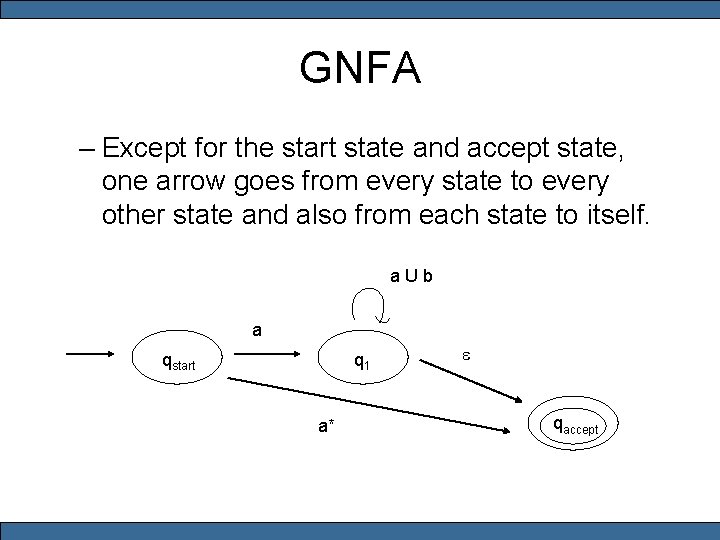
Part II • A generalized nondeterministic finite automaton (GNFA): – The start state has transition arrows going to every other state but no arrows coming in from any other state. – There is only a single accept state, and it has arrows coming in from every other state but no arrows going to any other state. Furthermore, the accept state is not the same as the start state

GNFA – Except for the start state and accept state, one arrow goes from every state to every other state and also from each state to itself. a U b a qstart q 1 a* e qaccept

GNFA Definition • A generalized nondeterministic finite automaton, (Q, S, d, qstart, qaccept) is a 5 tuple where – Q is the finite set of states – S is the input alphabet – d : (Q – {qaccept}) x (Q – {qstart}) R is the transition function – qstart is the start state – qaccept is the accept state

GNFA Acceptance • A GNFA accepts a string w in S* if w = w 1 w 2…wk where each wi is in S* and a sequence of states q 0, q 1, …qk exists such that – q 0 = qstart – qk = qaccept – for each i, wi e L(Ri) where Ri = d(qi-1, qi)

Part II: Proof Process • • • Start with a k state DFA Construct a k+2 state GNFA Map to a k+1 state GNFA …. . Map to a 2 state GNFA Read off the regular expression!

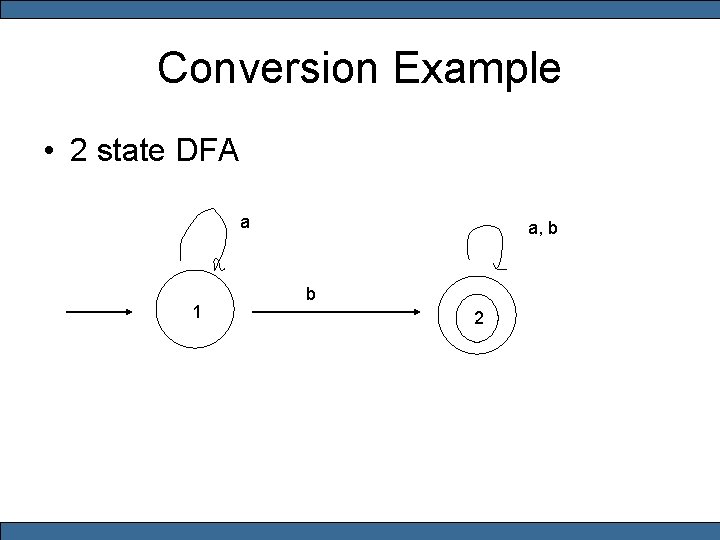
Conversion Example • 2 state DFA a 1 a, b b 2

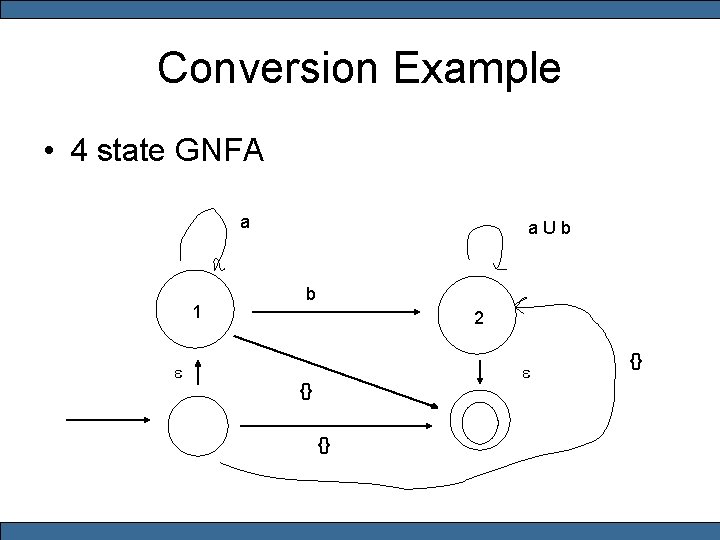
Conversion Example • 4 state GNFA a 1 e a U b b 2 e {} {} {}

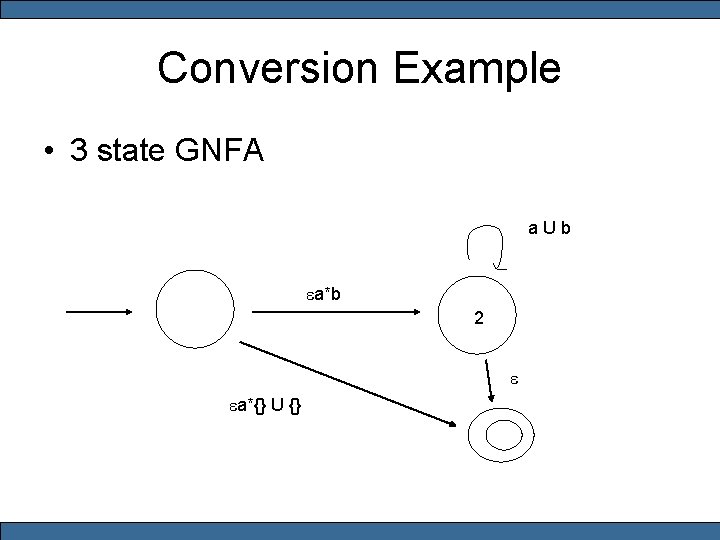
Conversion Example • 3 state GNFA a U b ea*b 2 e ea*{} U {}

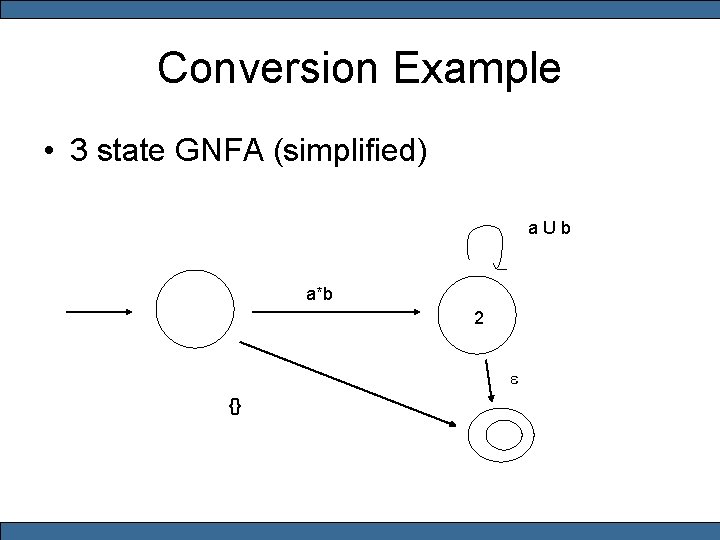
Conversion Example • 3 state GNFA (simplified) a U b a*b 2 e {}

Conversion Example • 2 state GNFA Regular Expression: a*b(a U b)* {} U a*b(a U b)*e

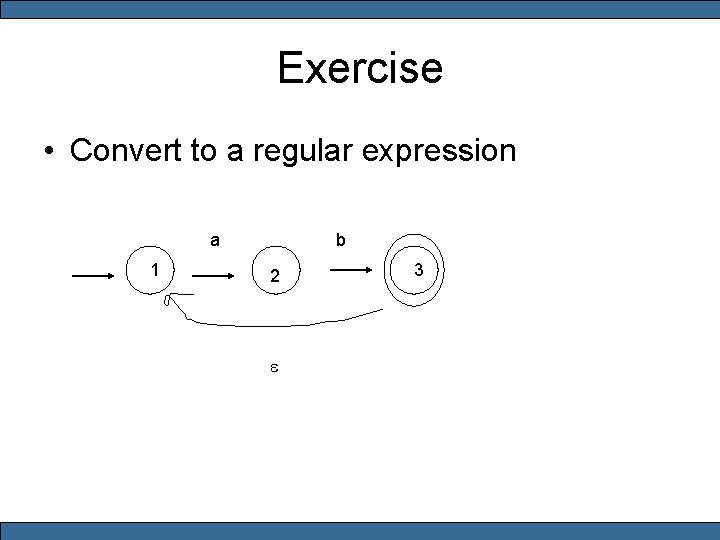
Exercise • Convert to a regular expression a 1 b 2 e 3