Introduction to the Theory of Computation John Paxton

Introduction to the Theory of Computation John Paxton Montana State University Summer 2003

Humor • A little boy, who wanted $100. 00 very badly, prayed for two weeks but nothing happened. Then he decided to write GOD a letter requesting $100. When the postal authorities received the letter to GOD, U. S. A. , they decided to send it to the President. The President was so impressed, touched, and amused that he instructed his secretary to send the boy $50. 00. Mr. President thought that this would appear to be a lot of money to the little boy. The little boy was delighted with the $50. 00 and immediately sat down to write a thank you note to GOD that read: "Dear God, Thank you very much for sending me the money. However, I noticed that for some reason you had to send it through Washington, D. C. , and, as usual, those devil's took half of it.

2. 2 Pushdown Automata • Fundamentally, an NFA with a stack • A recognizer • Equivalent to a Context Free Grammar • A CFG is a generator

PDA Definition • 1. 2. 3. 4. 5. 6. A PDA is a 6 -tuple (Q, S, Γ, d , q 0, F) where Q is the set of states S is the input alphabet Γ is the stack alphabet d: Q x Se x Γe P(Q x Γe ) is transition q 0 is the start state F ≤ Q is the set of accept states

Acceptance • A pushdown automaton M accepts input w if w can be written w 1 w 2…wm where each wi Se and states r 0, r 1, …rm Q and strings s 0, s 1, … sm Γ* exist that satisfy 1. r 0 = q 0 and s 0 = e 2. (ri+1, b) d(ri, wi+1, a) where si = at and si+1 = bt 3. rm F

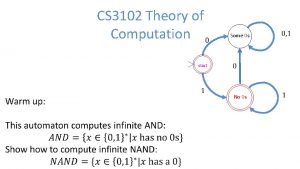
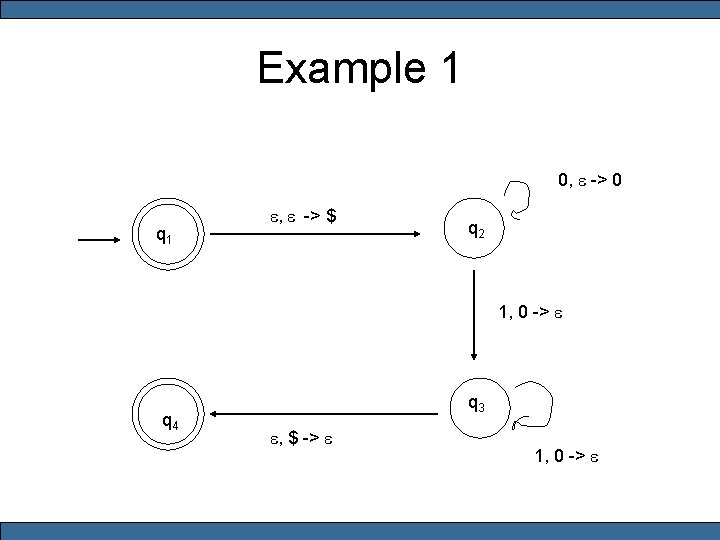
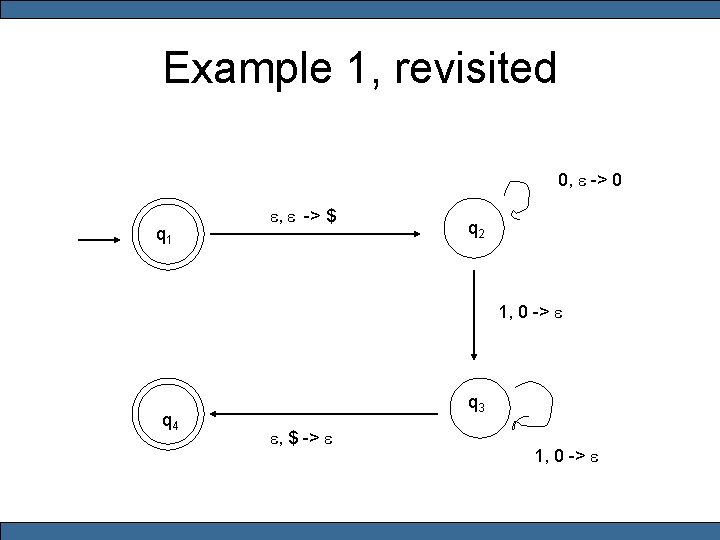
Example 1 • • • Q = {q 1, q 2, q 3, q 4} S = {0, 1} F = {0, $} F = {q 1, q 4} d(q 1, e, e) = (q 2, $) d(q 2, 0, e) = (q 2, 0) d(q 2, 1, 0) = (q 3, e) d(q 3, e, $) = (q 4, e)

Example 1 0, e -> 0 q 1 e, e -> $ q 2 1, 0 -> e q 4 q 3 e, $ -> e 1, 0 -> e

Exercise • Show a PDA that recognizes the language {aibjck | i, j, k >= 0 and i = j or j = k}. • Draw a picture. • Show it formally, (Q, S, Γ, d , q 0, F).

Exercise • Show a PDA that recognizes the language { ww. R | w {0, 1}* • Draw a picture. • Show it formally.

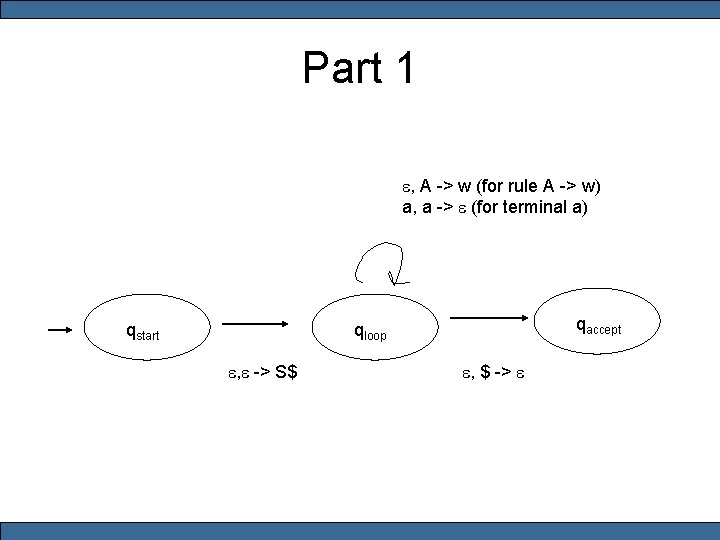
Theorem: PDAs and CFGs are equivalent • Part 1: If a language is context free, then some pushdown automaton recognizes it. • Part 2: If a pushdown automaton recognizes some language, then it is context free.

Part 1 e, A -> w (for rule A -> w) a, a -> e (for terminal a) qstart qaccept qloop e, e -> S$ e, $ -> e

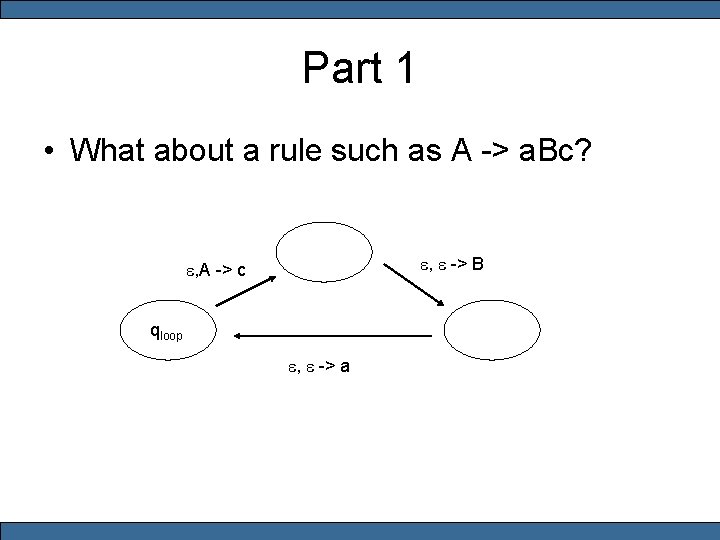
Part 1 • What about a rule such as A -> a. Bc? e, e -> B e, A -> c qloop e, e -> a

Exercise • Construct a PDA that is equivalent to the following CFG • S -> a. Tb | b • T -> Ta | e

Part 2 • Construct the PDA such that 1. It has a single accept state qaccept 2. It empties its stack before accepting 3. Each transition either pushes a symbol onto the stack (a push move) or pops one off the stack (a pop move), but does not do both at the same time.

Construction • The start variable is q 0 qaccept • The variables are qiqj • if d(p, a, e) contains (r, t) and d(s, b, t) contains (q, e), then add qpqq -> aqrsb • add qpq -> qprqrq for all p, q, r • add qpp -> e for all p

Example 1, revisited 0, e -> 0 q 1 e, e -> $ q 2 1, 0 -> e q 4 q 3 e, $ -> e 1, 0 -> e

Example 1, CFG • • q 11 -> e, q 22 -> e, etc. q 11 -> q 11 | q 12 q 21 | q 13 q 31 | q 14 q 41 q 14 -> eq 23 e q 23 -> 0 q 231 • Example derivation: q 14 -> q 23 -> 0 q 231 -> 00 q 2311 -> 0011

Corollary • Every regular language is context free regular languages context-free languages