Introduction lalgorithmique Introduction Algorithme Procdure dcrivant tape par

Introduction à l’algorithmique

Introduction • • • Algorithme: Procédure décrivant, étape par étape, une méthode permettant de résoudre un problème. Mot provenant du nom d’un mathématicien arabe du IXeme siècle El-Khawarizmi C’est la base de tout programme informatique Exemple: Recette de la sauce blanche: 1. 2. 3. 4. Faire revenir l’oignon haché fin dans du beurre, Ajouter la farine, bien mélanger; Rajouter le lait chaud, et mélanger pour éviter les grumeaux; Laisser mijoter 15 minutes

Algorithme: Suite finie d’instructions vérifiant: • Chaque étape est décrite de façon précise; • Chaque étape est déterministe: produit des résultats uniques; • L’algorithme s’arrête après un nb fini d’instructions • Reçoit des données en entrée; • Produit des données en sortie; • Généralité: Applicable à des ensembles différents de données d’entrée

Différence entre problème et instance du problème • Exemple d’un problème: Tri d’un ensemble d’éléments – Entrée: Suite de n éléts a 1, …an – Sortie: La suite réordonnée • Instances du problème: – Suite de nombres: 475, 787, 34, 245, 56, 350 – Suite de noms: Pierre, Christine, Sylvie, Samuel, Fabien

Exemple d’un algorithme 1. x : = a; 2. Si b>x, alors x : = b; 3. Si c>x, alors x : = c; : = Opérateur d’assignation y : = z signifie ``copie la valeur de z dans y’’. Valeur de z inchangée Paramètres d’entrée: a, b, c Valeur de sortie: x = max (a, b, c)

Pseudo-Code Algorithme maximum: Retourne le maximum de 3 entiers • Entrée: Trois entiers a, b, c; • Sortie: x contenant la valeur maximale parmi a, b, c 1. Procédure max(a, b, c) 2. x : = a; 3. Si b>x alors // Si b plus grand que x, mettre x à jour 4. x : = b; 5. Si c>x alors // Si c plus grand que x, mettre x à jour 6. x : = c; 7. Retourner (x) 8. Fin max Trace de l’algorithme pour: a=1; b=5; c=3 x=1 x=5

Pseudo-Code: Notation proche du code des langages de programmation (C, Pascal). Notation standard mais pas rigoureuse • • Titre de l’algorithme, description brève, entrées, sorties Procédures consécutives Numéroter les lignes (facultatif) Procédure commence par le mot ``Procédure’’, suivit du nom, suivit des paramètres Instructions (lignes exécutables) entre ``Procédure’’ et ``Fin’’, exécutées l’une après l’autre Bloc d’instructions entre ``Début’’ et ``Fin’’ Ligne de commentaires signalée par // (ou /* */) ``Retourne (x)’’ termine une procédure et retourne la valeur de x

Instruction Si-Alors-Sinon (If-Then-Else) Si p alors Si condition p vérifiée, exécuter action Si p alors action 1; Si condition p vérifiée, exécuter action 1. Sinon, exécuter action 2. Sinon action 2; Si x ≥ 0 alors Début x : = x-1; a : = b+c; Fin Bloc de conditions entre Début et Fin.

Instruction Tant que p Faire action; Tant que p est vrai exécuter action Algorithme Plus-Grand-Element: Retourne la plus grande valeur d’une liste Entrée: n entiers S 1, …, Sn Sortie: grand contenant le plus grand élément Trace de l’algorithme: n=4; S 1= -2; S 2=6; S 3=5; S 4=6 grand =-2 Procédure plus-grand (S, n) grand : = S 1; i: =2; Tant que i ≤ n Faire Début Si Si > grand alors // une plus grande valeur a été trouvée grand : = Si; i : = i+1; Fin Retourne (grand) Fin plus-grand; grand = 6 i=2 i=3 i=4 i=5

Instruction Pour (For) Pour var : = init à limite Faire action; À chaque passage dans la boucle, var est incrémenté de 1. On s’arrête dès que var > limite Algorithme Plus-Grand-Element: Réécriture de l’algorithme précédent mais avec une boucle ``Pour’’ Entrée: n entiers S 1, …, Sn Sortie: grand contenant le plus grand élément Procédure plus-grand (S, n) grand : = S 1; Pour i =1 à n Faire Si Si > grand alors // une plus grande valeur a été trouvée grand : = Si; Retourne (grand) Fin plus-grand;

Subdivision d’un problème en sousproblèmes (plusieurs procédures) • Problème: Trouver le plus petit nombre premier strictement supérieur à un entier positif donné – Procédure pour déterminer si un entier m est un nombre premier. Il suffit de tester si m est divisible par un entier entre 2 et m/2 – Utiliser cette procédure pour trouver le plus petit nombre premier p supérieur à un entier n.

Entrée: Un entier positif m Entrée: Un entier positif n Sortie: Vrai si m est premier, Faux si non. Sortie: Le plus petit nb premier m > n Procédure est-premier (m) Procédure premier-plus-grand (n) Pour i : = 2 à ENT(m/2) Faire Si m mod i = 0 alors // i divise m Retourne (Faux) Retourne (Vrai) Fin est-premier Trace de premier-plus-grand pour n=8: m=9 m = 10 m = 11 m : = n+1; Tant que est-premier(m) est Faux Faire m : = m+1; Retourne(m) Fin est-premier Trace dede est-premier pour m=9: m=11: m=10: i=2 i=3 i=5 11 9 mod 10 mod 222===110 9 mod 3 = 0 11 mod 5 = 1

Algorithme d’Euclide • Trouver le plus grand diviseur commun (pgcd) de deux entiers Définition: q est un diviseur commun de m et n si q divise à la fois m et n (le reste de la division entière est 0) Le pgdc de m et n est le plus grand entier q divisant à la fois m et n. Exemple: pgcd(4, 6) = 2; pgcd(3, 8) = 1; pgcd(9, 12) = 3; Utile pour la simplification de fractions: 9/12 = 3. 3/4. 3 = 3/4

Théorème 1: Soient m, n et c trois entiers 1. 2. 3. Si c est un diviseur commun de m et n, alors c divise (m+n). Si c est un diviseur commun de m et n, alors c divise (m-n). Si c divise m, alors c divise mn Soient a, b deux entiers >0. Si on divise a par b, on obtient un reste r et un quotient q vérifiants: a = bq+r, avec 0≤r<b, et q≥ 0 À l’aide du théorème 1 on montre: Théorème 2: Soient a, b deux entiers positifs. Soient q le quotient et r le reste de la division entière de a par b. Alors pgcd(a, b) = pgcd(b, r)

Trouver le PGCD de a et b Exemple: pgcd(30, 105) • 1ère méthode: Trouver tous les diviseurs de a et b, et trouver le diviseur commun le plus grand – Diviseurs de 30: 1, 2, 3, 5, 6, 10, 15, 30 – Diviseurs de 105: 1, 3, 5, 7, 15, 21, 35, 105 Þ pgcd(30, 105) = 15 • 2ème méthode: Utiliser le théorème 2 – 105 = 30. 3 + 15. Donc pgcd(105, 30) = pgcd(30, 15) – 30 = 15. 2 + 0. Donc pgcd(30, 15) = pgcd(15, 0) – pgcd(15, 0)=15 Þ pgcd(105, 30)=pgcd(30, 15)=pgcd(15, 0)=15 La méthode 2 est la méthode d’Euclide

Méthode d’Euclide Soient r 0, r 1 deux entiers strictement positifs, tels que r 0=r 1. q+r 2 avec 0≤r 2<r 1 • Si r 2 = 0, pgcd (r 0, r 1) = r 1 • Sinon, rediviser ri par ri+1 tant que ri+1 est différent de 0 • Si rn est le premier reste nul, alors pgcd(r 0, r 1) = pgcd(r 1, r 2) = … =pgcd(rn-1, rn)= pgcd(rn-1, 0) = rn-1

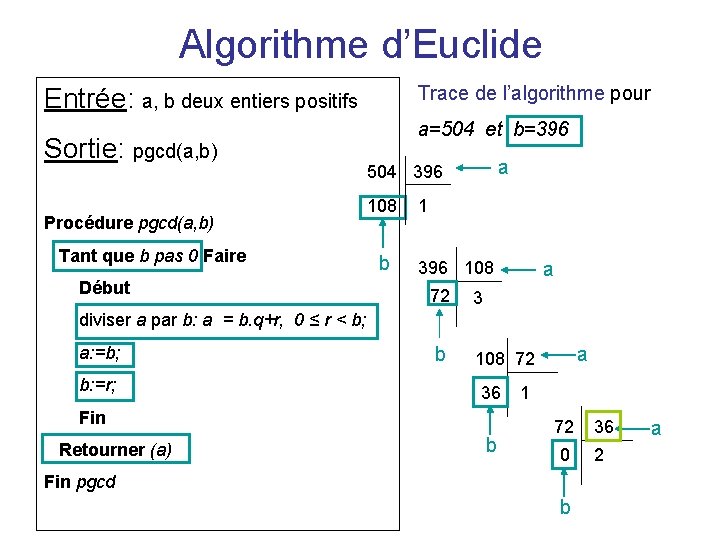
Algorithme d’Euclide Trace de l’algorithme pour Entrée: a, b deux entiers positifs Sortie: pgcd(a, b) Procédure pgcd(a, b) Tant que b pas 0 Faire Début a=504 et b=396 a 504 396 108 b 1 396 108 72 a 3 diviser a par b: a = b. q+r, 0 ≤ r < b; a: =b; b: =r; b 36 Fin Retourner (a) a 108 72 b 1 72 36 0 2 Fin pgcd b a

Procédure récursive • Procédure qui s’invoque elle-même Exemple: n! = n(n-1)(n-2)… 2. 1 Si n≥ 0 0! = 1 n! = n(n-1)! pour n≥ 1 5! = 5. 4! = 120 4! = 4. 3! = 24 3! = 3. 2! =6 2! = 2. 1! =2 1! = 1. 0! =1 • Toute procédure récursive doit avoir une condition d’arrêt: cas de base qui permet de ne plus invoquer la procédure. Ici, la condition d’arrêt est n=0

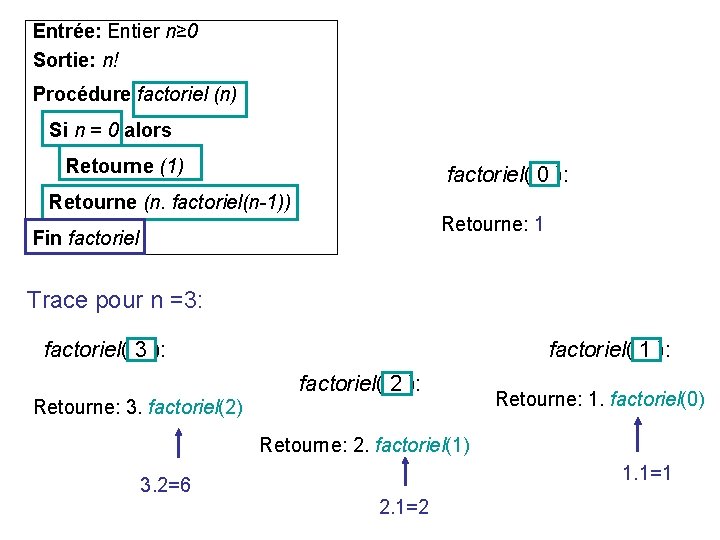
Entrée: Entier n≥ 0 Sortie: n! Procédure factoriel (n) Si n = 0 alors Retourne (1) factoriel( 0 ): Retourne (n. factoriel(n-1)) Retourne: 1 Fin factoriel Trace pour n =3: factoriel( 3 ): factoriel( 1 ): factoriel( 2 ): Retourne: 3. factoriel(2) Retourne: 1. factoriel(0) Retourne: 2. factoriel(1) 1. 1=1 3. 2=6 2. 1=2

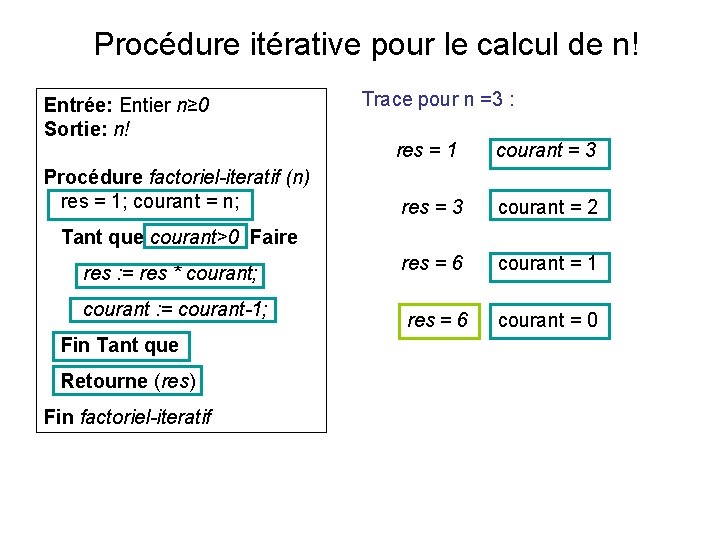
Procédure itérative pour le calcul de n! Entrée: Entier n≥ 0 Sortie: n! Procédure factoriel-iteratif (n) res = 1; courant = n; Trace pour n =3 : res = 1 courant = 3 res = 3 courant = 2 res = 6 courant = 1 res = 6 courant = 0 Tant que courant>0 Faire res : = res * courant; courant : = courant-1; Fin Tant que Retourne (res) Fin factoriel-iteratif

Procédure récursive pour le calcul du pgcd Entrée: a, b deux entiers >0 Sortie: pgcd(a, b) pgcd-rec(108, 72) Procédure pgcd-rec (a, b) 108 = 72. 1 + 36 Si b = 0 alors pgcd-rec(72, 36) Retourner (a); 36 diviser a par b: a = b. q+r, 0 ≤ r < b; pgcd-rec(36, 0) Retourner (pgcd-rec (b, r)) Fin pgcd-rec 36 Trace pour a=504 et b=396: pgcd-rec(396, 108) pgcd-rec(36, 0) 396 = 108. 3 + 72 pgcd-rec(504, 396) pgcd-rec(108, 72) 504 = 396. 1 + 108 pgcd-rec(396, 108) pgcd-rec(72, 36) 36 36 36

Nombres de Fibonacci Exemple: Un robot peu avancer par des pas de 1 ou 2 mètres. Calculer le nombre de façons différentes de parcourir une distance de n mètres Distance Suite de pas Nb de possibilités 1 1 1 2 1, 1 ou 2 2 3 1, 1, 1 ou 1, 2 ou 2, 1 3 4 1, 1, 1, 1 ou 1, 1, 2 ou 1, 2, 1 ou 2, 1, 1 ou 2, 2 5

• Pas(n): Nombre de possibilités pour parcourir n mètres. • Pas(1) = 1, Pas(2) = 2; • Pour n>2: – Si premier pas = 1 mètres, il reste n-1 mètres -> Pas(n-1) – Si premier pas = 2 mètres, il reste n-2 mètres -> Pas(n-2) Entrée: n Sortie: Pas(n) Procédure pas-robot (n) Si n=1 ou n=2 alors Retourne (n) Retourne (Pas(n-1) + Pas(n-2) ) Fin pas-robot Donc, Pas(n) = Séquence de Fibonacci: Pas(n-1)+Pas(n-2) f =1 1 f 2 = 2 fn = fn-1 + fn-2 pour n>2