SIMPLIFICATION DUNE RACINE CARREE Prendre la racine carre






- Slides: 8

SIMPLIFICATION D’UNE RACINE CARREE

Prendre la racine carrée d’un nombre positif consiste à cher un nombre positif dont le carré est le nombre situé sous le radical. Par exemple, pour calculer la racine carrée de 25, nous devons recher un nombre positif dont le carré est 25. Ce nombre existe et est égal à … 5. Tout nombre positif a une racine carrée. Le nombre 2 a une racine carrée, mais cette valeur ne peut pas s’écrire sous forme décimale, ni même sous forme d’une fraction. La racine carrée de 2 vaut environ 1, 414 mais n’est pas égal à 1, 414. mais le carré de 1, 414 ne donne pas 2. Ce carré est proche de 2 , mais différent : 1, 414² = 1, 9993969 ! La seule écriture possible de la racine carrée de 2 est ……. La racine carrée de 3, c’est-à-dire le nombre positif dont le carré est 3 s’écrit

Nous pouvons cependant « calculer » certaines racines carrées. Par exemple : Si nous ne considérons que les nombres entiers ( positifs ), certaines racines carrées se simplifient. Par exemple : s e l s Seule rrées ca s e n i rac s é r r a de c t n o s s it a f r a p. s r e i nt e s e d ; 144 … sontauappelés esdes Ces nombres 1 , 4 , 9 , 16 , 25 , 36 , 49 , 64 , 81 , 100 , 121 r t les carrés parfaits. ( Un carré parfait est le carré d’un nombre entier) s s u r o e T i t n e s e r b Ces carrés parfaits ( dont la racine carrée a une écriture nous permettre msimple ) vont d o s n e de simplifier certaines racines carrées. t n auro s e é r r a c s e racin onnelles. i

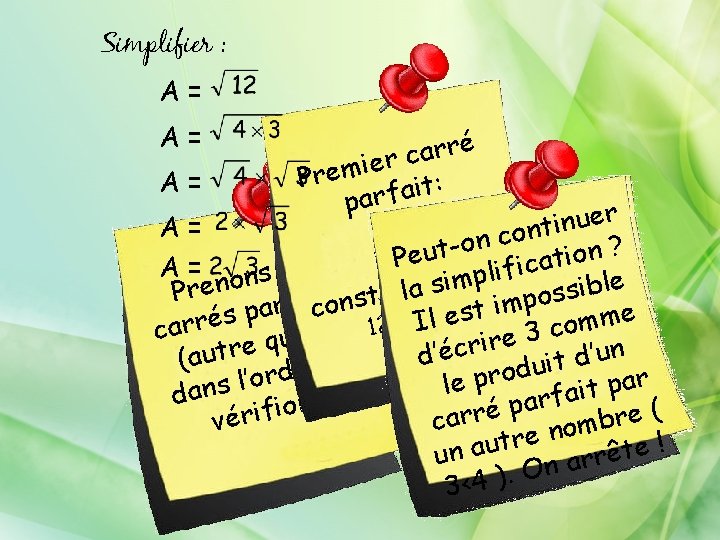
Simplifier : A= A= A= é r r a c r e i m e Pr : t i a f r pa r e u n i tlna : A= n o c n o i niosn ? oiuseqsute t s u u e o Q u P laotcrréiere P uelisf: iaclé N A = ons les r o u p a q n N c m e o s i l n t e n s b e t n n i o i a u a t s l c s Pr e n s a Pa 3 aiinmtp eborrreé 12 itonst r a f r c a t a unmeme p xem s c m s 4 o n é l = n u r ’ I 2 r e d l iliese 3 rcrsoo it 1 ) n u 1 ca u d e t u t r q p i e u r e s e t c r i e n m t é a u ’ d ’ u f m d d a é r t , ( ao opordiéutiatnrtrie e c r p é e r d r rpdrb’urne ce rirtépeasr o ’ p l e l s n aavaornsun m ne c o da f. n s r s a n p p o i i u c t é f o i i a r p a r r r f é v ca npoaurs : nom: bbrree? ( erniroem te ! r t u a e unautérc n arrê O. ) 4 < 3 4

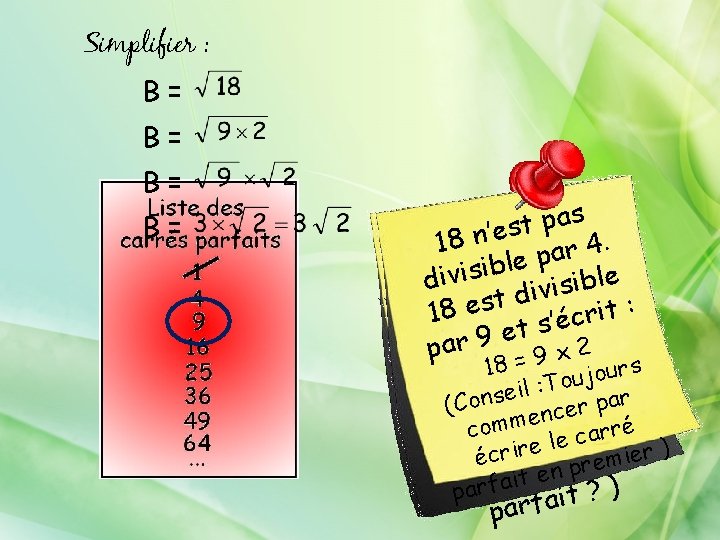
Simplifier : B= B= s a 8 1 p i t s s nh’oens 8. 1 c 4 r e r t h a i pdu C e l o b r i p s i it edsivt le t dipvaisrifbale srré e : a t 8 i c 1 r n c d’u 9 entasu’étre paprar u = 9 ’xes 2 t-à 1 r 8 e ( c ujours b eil : Toe que nom on: s est-ccer par (Ce le dircommednivicsaib é r r 18éecsrtire lecparrerméier ) nen u r t i a a p ) parf ? t i parfa

Simplifier : C= C= C= C = Donc C= C= C= s n o i v u o p s u No t n e m e égal le s è d , r e h c é r r cher a c n est. u , t u d déb. Mais l 1 u 8 s granle p divisibliere t i a f parencoreitdidveisfibaré t n car les f e u s 2 l I 7 par um. t: 9 n 4 e r a e r t 7 a p rappidparfadie 2 8 12 x 4 s n= = 9 x roénsc o 2 i s 7 i v i d 18 alevosncsardons ussous devqu’à 64 Ntoou. N ; s u r 1 j : e 8 u s t n a i i v i a t u f n r nc pcaorfait s pad s u o ré o r a N c. ) e (l à 72 r u e i pér u s t n : éta s n o av

EXERCICES Simplifier : Nous pouvions également écrire : Si 4 est un carré parfait, 36 l’est également. Nous pouvions également dire que 144 est un carré parfait : le carré de 12. D’où le résultat !

UN PEU PLUS LOIN. . e n u s n o Simplifier : . … Utilirsiété de la prop e: é r r a c racine Simplifier : f) i t i s o p (a e n i c a r Mais la e s e n 6 de e é r r a c ! s a p e i f simpli s r o l a s n o s o p m o Déc 6: 2 x 3 = 6 s u o n , e ous d a t s A c. Deevonnss-nnuovuosnnst e 18 ouoevusossapioreqm p. N en e r i u r c u c r é i oenrtaîtreore neérceem v apéigrael apnpta » a efnocrtm? e facontsioeuspal rfaai it, à f 2 « 1 c 2 arréé p 6 r a x r 2 O = UI. nc : r a c 1 n u 9 do r i s o n v aaveot s nc o s d u s o N pouvon e N r s t u î O o a N r N a p p a. re i 8 a 1 f r e e l s o p m co é d t e