Intertemporal Choice 1 Intertemporal Choice Persons often receive

Intertemporal Choice 1

Intertemporal Choice Persons often receive income in “lumps”; e. g. monthly salary. n How is a lump of income spread over the following month (saving now for consumption later)? n Or how is consumption financed by borrowing now against income to be received at the end of the month? n 2

Present and Future Values Begin with some simple financial arithmetic. n Take just two periods; 1 and 2. n Let r denote the interest rate period. e. g. , if r = 0. 1 (10%) then $100 saved at the start of period 1 becomes $110 at the start of period 2. n 3

Future Value n The value next period of $1 saved now is the future value of that dollar. n Given an interest rate r the future value one period from now of $1 is n Given an interest rate r the future value one period from now of $m is 4

Present Value Suppose you can pay now to obtain $1 at the start of next period. n What is the most you should pay? n Would you pay $1? n No. If you kept your $1 now and saved it then at the start of next period you would have $(1+r) > $1, so paying $1 now for $1 next period is a bad deal. n 5

Present Value Q: How much money would have to be saved now, in the present, to obtain $1 at the start of the next period? n A: $m saved now becomes $m(1+r) at the start of next period, so we want the value of m for which m(1+r) = 1 That is, m = 1/(1+r), the present-value of $1 obtained at the start of next period. n 6

Present Value n The present value of $1 available at the start of the next period is n And the present value of $m available at the start of the next period is n E. g. , if r = 0. 1 then the most you should pay now for $1 available next period is $0. 91 7

The Intertemporal Choice Problem Let m 1 and m 2 be incomes received in periods 1 and 2. n Let c 1 and c 2 be consumptions in periods 1 and 2. n Let p 1 and p 2 be the prices of consumption in periods 1 and 2. n 8

The Intertemporal Choice Problem The intertemporal choice problem: Given incomes m 1 and m 2, and given consumption prices p 1 and p 2, what is the most preferred intertemporal consumption bundle (c 1, c 2)? n For an answer we need to know: n the intertemporal budget constraint ¨ intertemporal consumption preferences. ¨ 9

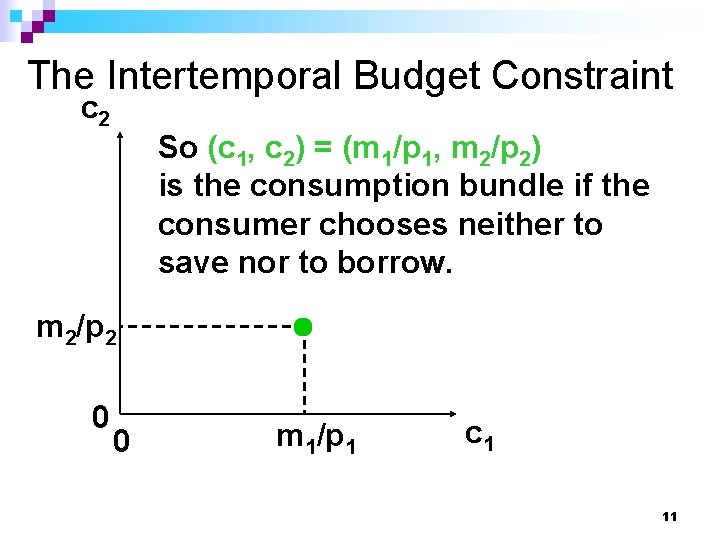
The Intertemporal Budget Constraint Suppose that the consumer chooses not to save or to borrow. n Q: What will be consumed in period 1? A: c 1 = m 1/p 1. n Q: What will be consumed in period 2? A: c 2 = m 2/p 2 n 10

The Intertemporal Budget Constraint c 2 So (c 1, c 2) = (m 1/p 1, m 2/p 2) is the consumption bundle if the consumer chooses neither to save nor to borrow. m 2/p 2 0 0 m 1/p 1 c 1 11

Intertemporal Choice n Suppose c 1 = 0, expenditure in period 2 is at its maximum at since the maximum we can save in period 1 is m 1 which yields (1+r)m 1 in period 2 n so maximum possible consumption in period 2 is 12

Intertemporal Choice n Conversely, suppose c 2 = 0, maximum possible expenditure in period 1 is since in period 2, we have m 2 to pay back loan, the maximum we can borrow in period 1 is m 2/(1+r) n so maximum possible consumption in period 1 is 13

The Intertemporal Budget Constraint c 2 m 2/p 2 0 0 m 1/p 1 c 1 14

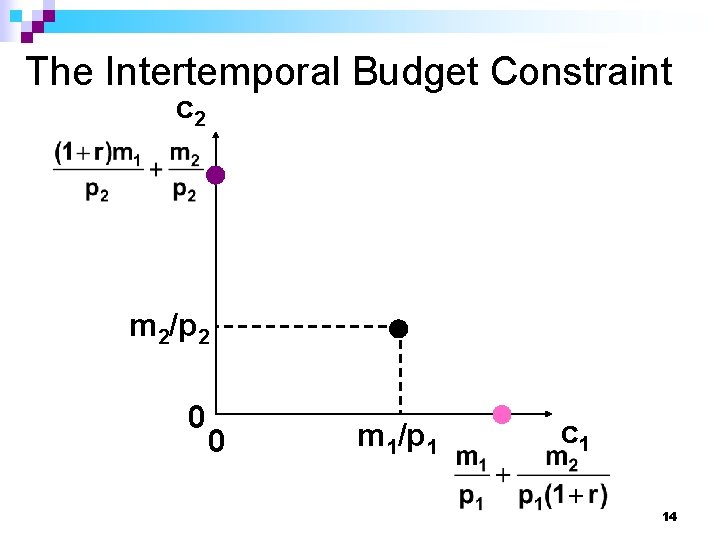
Intertemporal Choice n Finally, if both c 1 and c 2 are greater than 0. Then the consumer spends p 1 c 1 in period 1, and save m 1 - p 1 c 1. Available income in period 2 will then be so 15

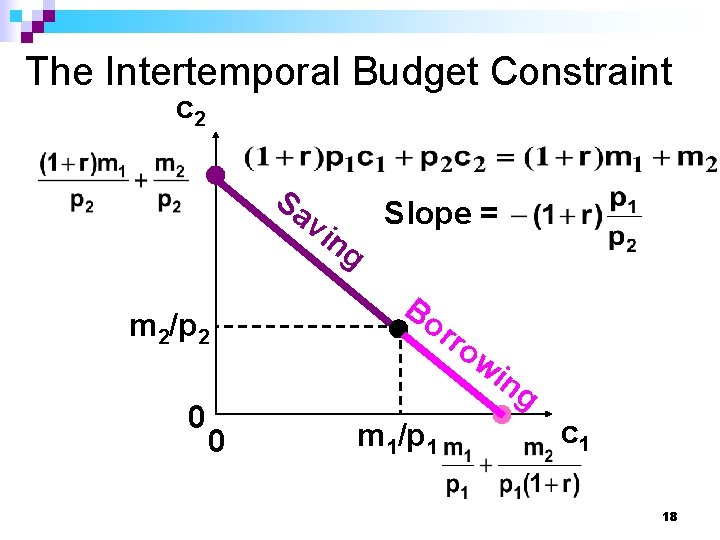
Intertemporal Choice n Rearrange to get the future-value form of the budget constraint since all terms are expressed in period 2 values. n Rearrange to get the present-value form of the budget constraint where all terms are expressed in period 1 values. 16

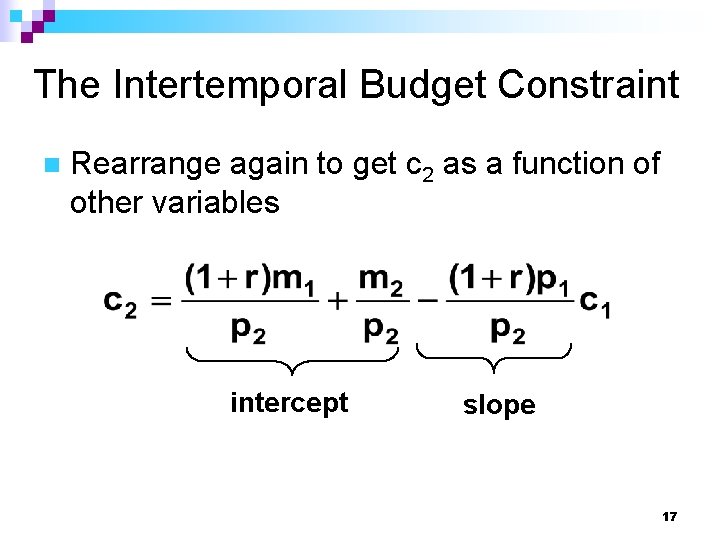
The Intertemporal Budget Constraint n Rearrange again to get c 2 as a function of other variables intercept slope 17

The Intertemporal Budget Constraint c 2 Sa vi m 2/p 2 0 0 ng Slope = Bo rro wi m 1/p 1 ng c 1 18

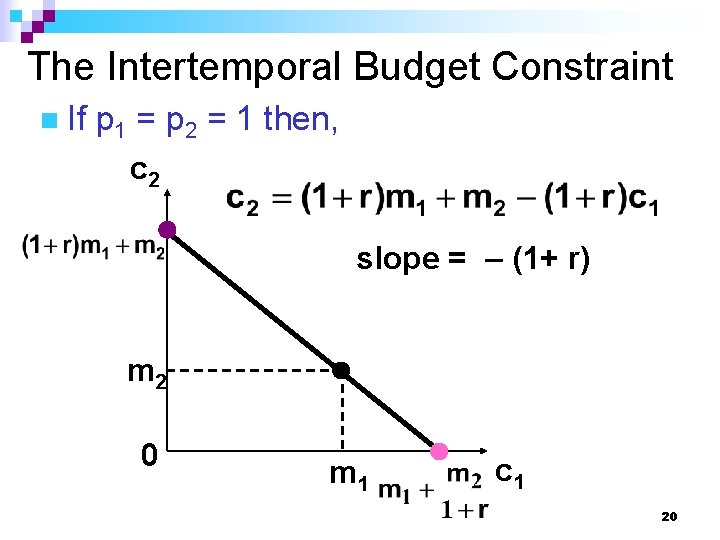
The Intertemporal Budget Constraint n n Suppose p 1 = p 2 = constraint becomes 1, the future-value Rearranging, we get 19

The Intertemporal Budget Constraint n If p 1 = p 2 = 1 then, c 2 slope = – (1+ r) m 2 0 m 1 c 1 20

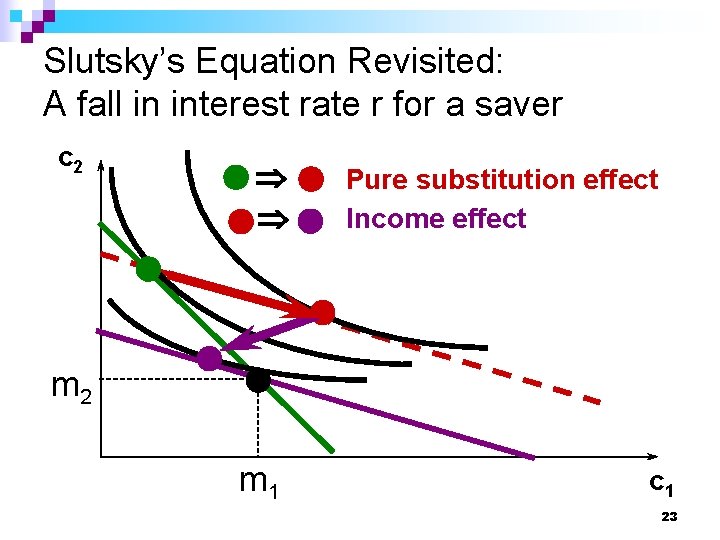
Slutsky’s Equation Revisited n Recall that Slutsky’s equation is ∆xis (ωi – x i) ∆xim ∆pi + ∆m n An increase in r acts like an increase in the price of c 1. If p 1 = p 2 = 1, ω1 = m 1 and x 1 = c 1. In this case, we write Slutsky’s equation as ∆c 1 s (m 1 – c 1) ∆c 1 m + ∆r ∆r ∆m 21

Slutsky’s Equation Revisited n n ∆c 1 s (m 1 – c 1) ∆c 1 m + ∆r ∆r ∆m If r decreases, substitution effect leads to an ……………. . in c 1 Assuming that c 1 is a normal good then ¨ if the consumer is a saver m 1 – c 1 > 0 then income effects leads to a …. . . in c 1 and total effect is ……. . . ¨ if the consumer is a borrower m 1 – c 1 < 0 then income effects leads to a …. . in c 1 and total effect must be ……………. 22

Slutsky’s Equation Revisited: A fall in interest rate r for a saver c 2 Þ Þ Pure substitution effect Income effect m 2 m 1 c 1 23

Price Inflation n n Define the inflation rate by p where For example, p = 0. 2 means 20% inflation, and p = 1. 0 means 100% inflation. 24

Price Inflation n We lose nothing by setting p 1=1 so that p 2 = 1+ p Then we can rewrite the future-value budget constraint as n And rewrite the present-value constraint as n 25

Price Inflation rearranges to intercept slope 26

Price Inflation When there was no price inflation (p 1=p 2=1) the slope of the budget constraint was -(1+r). n Now, with price inflation, the slope of the budget constraint is -(1+r)/(1+ p). This can be written as n r is known as the real interest rate. 27

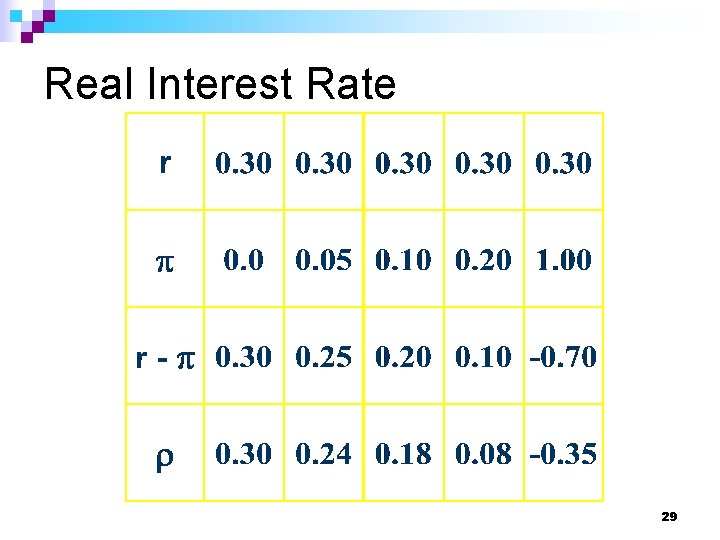
Real Interest Rate gives For low inflation rates (p » 0), r » r - p. For higher inflation rates this approximation becomes poor. 28

Real Interest Rate 29

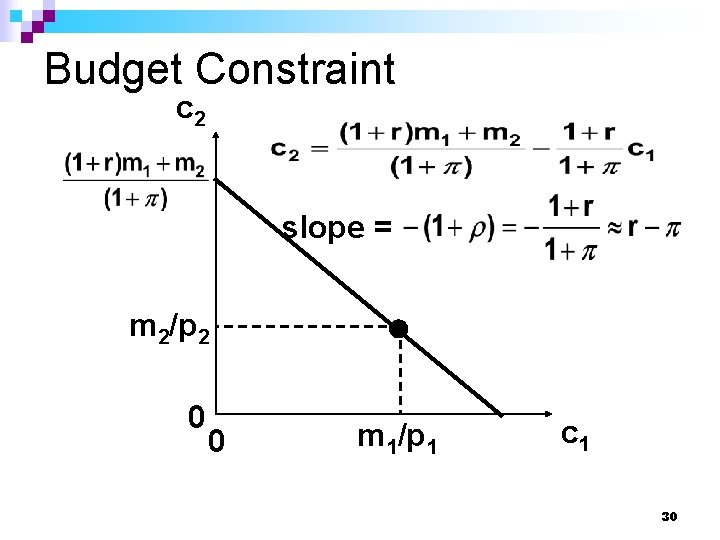
Budget Constraint c 2 slope = m 2/p 2 0 0 m 1/p 1 c 1 30

Budget Constraint n The slope of the budget constraint is n The constraint becomes flatter if the interest rate r falls or the inflation rate p rises (both decrease the real rate of interest). 31

Comparative Statics n Using revealed preference, we can show that If a saver continue to save after a decrease in real interest rate , then he will be worse off ¨ A borrower must continue to borrow after a decrease in real interest rate , and he must be better off ¨ 32

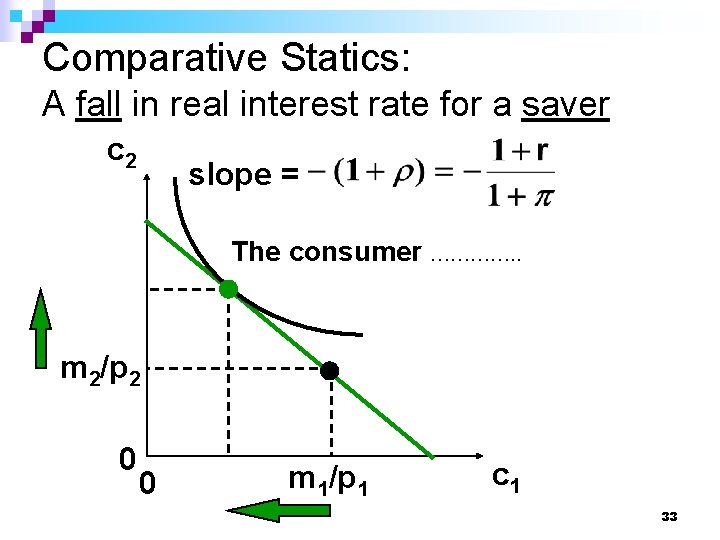
Comparative Statics: A fall in real interest rate for a saver c 2 slope = The consumer …………. . m 2/p 2 0 0 m 1/p 1 c 1 33

Comparative Statics: A fall in real interest rate for a saver c 2 m 2/p 2 0 An increase in the inflation rate or a decrease in the interest rate ……. . …… the budget constraint. m 1/p 1 c 1 34

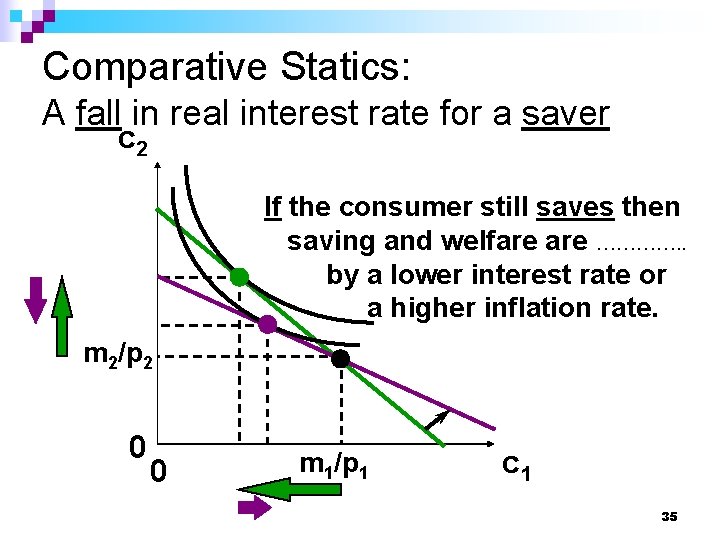
Comparative Statics: A fall in real interest rate for a saver c 2 If the consumer still saves then saving and welfare …………. . by a lower interest rate or a higher inflation rate. m 2/p 2 0 0 m 1/p 1 c 1 35

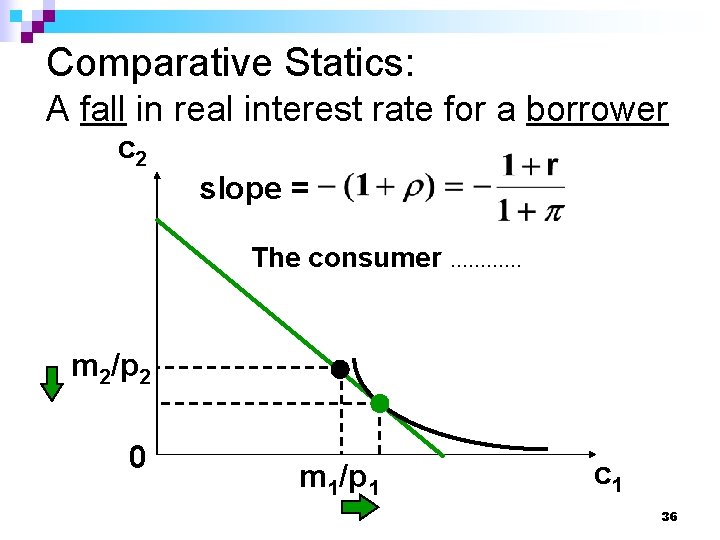
Comparative Statics: A fall in real interest rate for a borrower c 2 slope = The consumer ………… m 2/p 2 0 m 1/p 1 c 1 36

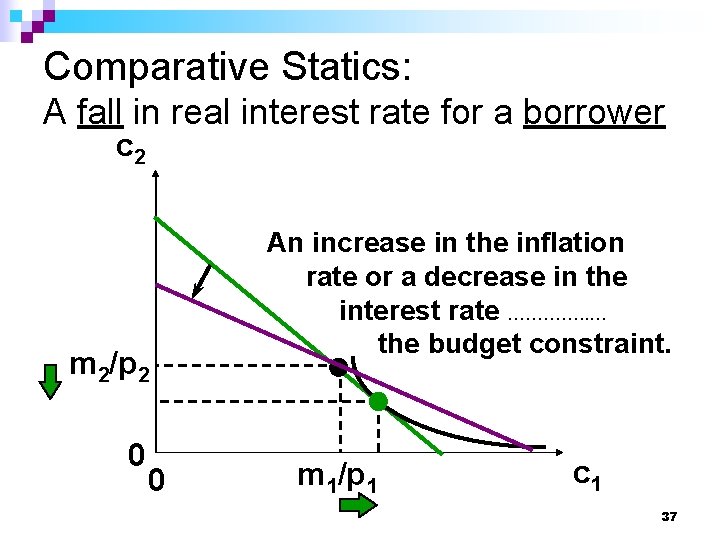
Comparative Statics: A fall in real interest rate for a borrower c 2 m 2/p 2 0 0 An increase in the inflation rate or a decrease in the interest rate …………. . … the budget constraint. m 1/p 1 c 1 37

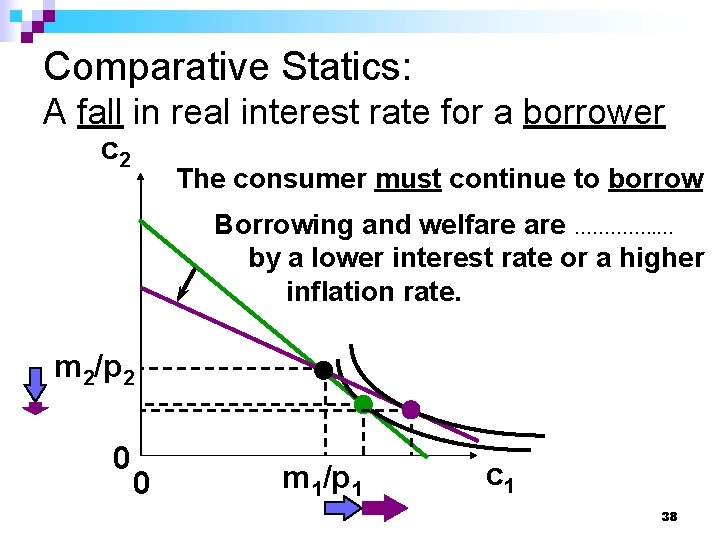
Comparative Statics: A fall in real interest rate for a borrower c 2 The consumer must continue to borrow Borrowing and welfare …………. . … by a lower interest rate or a higher inflation rate. m 2/p 2 0 0 m 1/p 1 c 1 38

Valuing Securities A financial security is a financial instrument that promises to deliver an income stream. n E. g. ; a security that pays $m 1 at the end of year 1, $m 2 at the end of year 2, and $m 3 at the end of year 3. n What is the most that should be paid now for this security? n 39

Valuing Securities n The security is equivalent to the sum of three securities; ¨ the first pays only $m 1 at the end of year 1, ¨ the second pays only $m 2 at the end of year 2, and ¨ the third pays only $m 3 at the end of year 3. 40

Valuing Securities n The PV of $m 1 paid 1 year from now is n The PV of $m 2 paid 2 years from now is n The PV of $m 3 paid 3 years from now is n The PV of the security is therefore 41

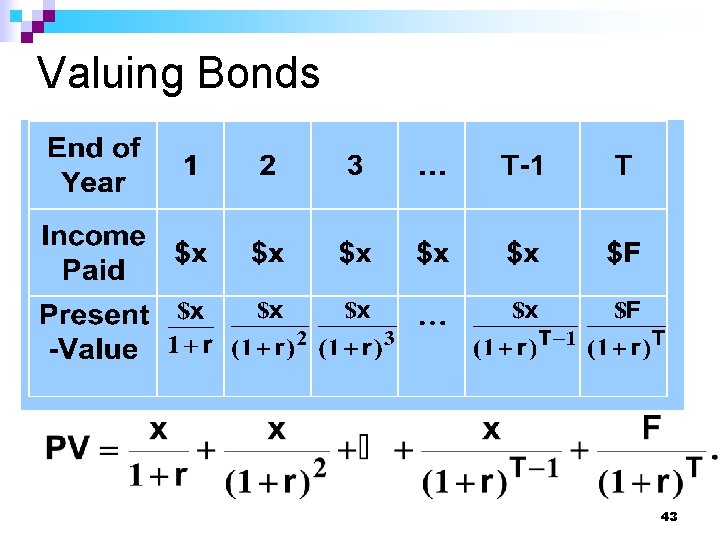
Valuing Bonds A bond is a special type of security that pays a fixed amount $x for T years (its maturity date) and then pays its face value $F. n What is the most that should now be paid for such a bond? n 42

Valuing Bonds 43

Valuing Bonds n Suppose you win a State lottery. The prize is $1, 000 but it is paid over 10 years in equal installments of $100, 000 each. What is the prize actually worth? 44

Valuing Bonds is the actual (present) value of the prize. 45

Valuing Consols A consol is a bond which never terminates, paying $x period forever. n What is a consol’s present-value? n 46

Valuing Consols 47

Valuing Consols Solving for PV gives 48

Valuing Consols E. g. if r = 0. 1 now and forever then the most that should be paid now for a console that provides $1000 per year is 49