Inference Rules and Proofs Z Program Specification and

Inference Rules and Proofs (Z); Program Specification and Verification 1

Propositional logic The Z methodology is based on propositional logic basic operators of propositional logic: conjunction (AND); disjunction (OR); implication ( ); equivalence ( ) ; negation (NOT, ~) propositions--statements about the system tautologies--propositions which are always true (A = A) contradictions--propositions which are never true (A = not A) 2

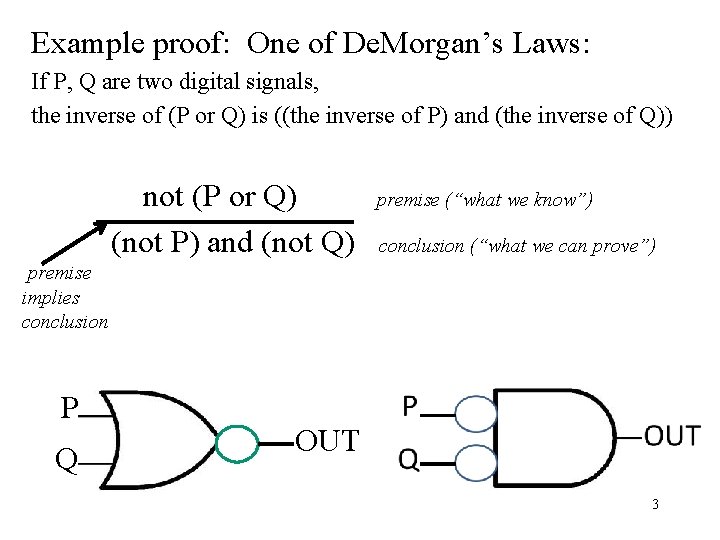
Example proof: One of De. Morgan’s Laws: If P, Q are two digital signals, the inverse of (P or Q) is ((the inverse of P) and (the inverse of Q)) not (P or Q) (not P) and (not Q) premise (“what we know”) conclusion (“what we can prove”) premise implies conclusion P Q OUT 3

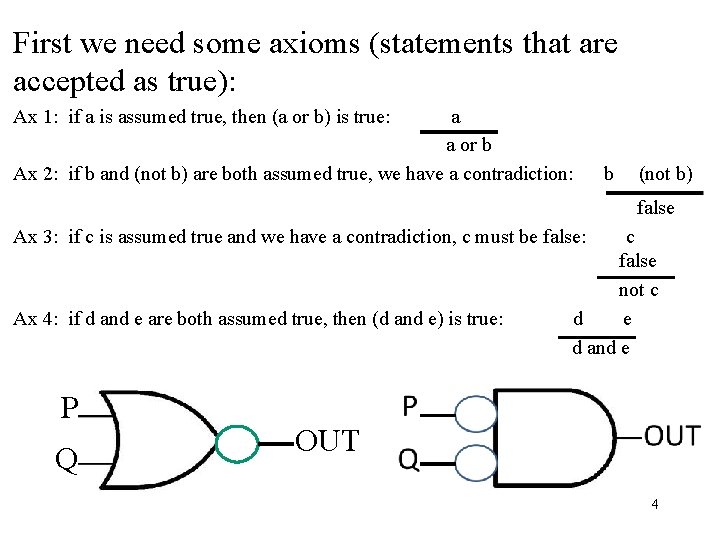
First we need some axioms (statements that are accepted as true): Ax 1: if a is assumed true, then (a or b) is true: a a or b Ax 2: if b and (not b) are both assumed true, we have a contradiction: b (not b) false Ax 3: if c is assumed true and we have a contradiction, c must be false: Ax 4: if d and e are both assumed true, then (d and e) is true: P Q c false not c d e d and e OUT 4

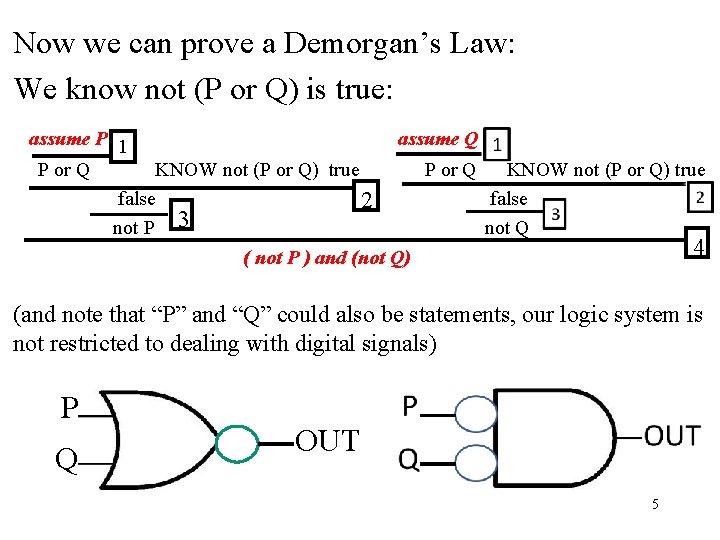
Now we can prove a Demorgan’s Law: We know not (P or Q) is true: assume P 1 assume Q P or Q KNOW not (P or Q) true false 2 not P 3 not Q 4 ( not P ) and (not Q) (and note that “P” and “Q” could also be statements, our logic system is not restricted to dealing with digital signals) P Q OUT 5

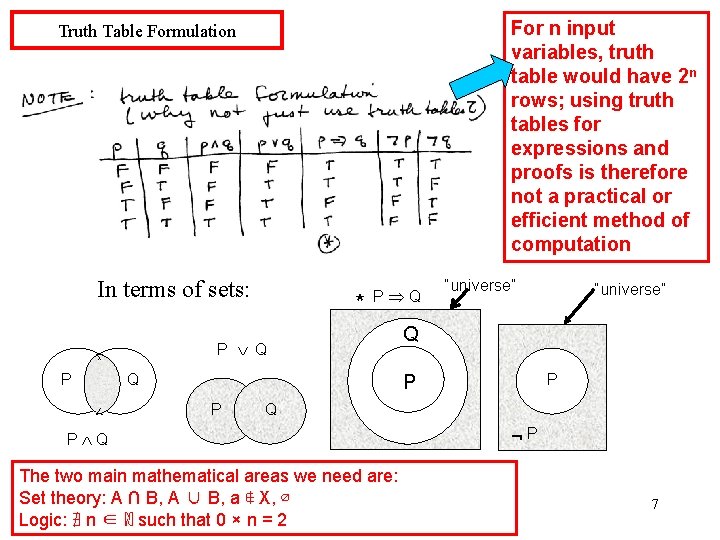
Question: why can’t we use a simpler approach, such as a truth table? Answer: a truth table proof would work in this simple case where P and Q can each take on only the values 0 or 1 and so we have only four possible choices for the inputs: 00, 01, 10, 11 But as the number of inputs to a circuit grows, the number of values in the truth table will grow exponentially (for n inputs, there are 2 n possible ways to assign 0’s and 1’s to the inputs). So a proof which relies on a truth table will quickly become intractably large. But a proof such as the one above which uses statements about the “state” of the circuit and logical rules will not avoids this problem. 6

For n input variables, truth table would have 2 n rows; using truth tables for expressions and proofs is therefore not a practical or efficient method of computation Truth Table Formulation In terms of sets: * P Q Q P PP P “universe” Q Q The two main mathematical areas we need are: Set theory: A ∩ B, A ∪ B, a ∉ X, ∅ Logic: ∄ n ∈ ℕ such that 0 × n = 2 P 7

Logical Operators 8

Inference Rule--Z Notation Abbreviations: “intro” = introduction “elim” = elimination 9

AND Rules 10

OR Rules 11

IMPLICATION rules (implication, equivalence) 12

NEGATION Rules 13

Proof example: AND is commutative 14

Proof example: OR is commutative 15

Exercise: associativity 16

Proof example: implication (1) 17

Proof example: implication (2) 18

Proof example: de. Morgan’s Law 19

Proof example: Law of the excluded middle 20

Example: specifying and deriving a program for linear search Specification: Informal: “write a program to search for an element in a table” Some questions not answered in this description: --how will the “table” be represented? --will the data be sorted? --if the element we are looking for is not in the table, what should the program do? 21

More exact specification leading to a program: --make T be a specific set (an interval [p, q) of “natural numbers”, ℕ) --describe the specification using mathematical logic p 1 ( p ∈ ℕ ) and ( q ∈ ℕ ) and p ≦ q 2. P: defined for all elements of [p, q) x? q Preconditions P 3. table-search-program returns 4. x with (x ∈ ℕ ) and ( p ≦ x ) and ( x ≦ q) 5. and P(x) if x < q Postconditions Q 6. and for all elements i of [p, q) (not P(i) ) if x = q 22

Deriving the program for linear search: need to add the idea of change of state caused by the execution of program statements. We will use a “Hoare triple” for this: {P} S {Q} “If precondition P is true and code statements S are executed, then postcondition Q will be true” (focuses on changes and invariants in each program step plus termination condition) Ex: { w real, w > 0 } S { a real y is output with y x y < w} Ex: {1, 2 on previous slide hold} [3 carried out] {4, 5, 6 hold} 23

Deriving the program: Basic form: while test do loop body done Some technical issues to address: --can’t actually have x = q, q is not in the set we are examining --must make sure program terminates --in practice must worry about “side conditions”, e. g. , of physical assignment in computer memory, “a : = b” is not simply a mathematical statement a = b We want postconditions Q to be true at loop exit We can define an invariant related to Q that is true before we enter the loop and each time we leave it And we can define a variant v, a non-negative integer that decreases at every loop iteration and is 0 when the loop ends, e. g. , q-x 24

Possible program: 1. x : = p; y : = q; 2. while x ≠ y do 3. if P(x) then y : = x else x : = x + 1 done; Proof that this program is correct: I ≝ I 1 and I 2 and I 3 I 1 ≝ (x ∈ ℕ ) and (y ∈ ℕ ) and ( p ≦ x ) and ( x ≦ y ) and ( y ≦ q ) I 2 ≝ for all j ∈ ℕ ((p ≦ j) and ( j < x)) implies (not (P(j))) I 3 ≝ y < q implies P(x) We can show by induction that I is an invariant for the loop And we can show that v = y –x is nonnegative, decreases each time through the loop, and is 0 at termination So the program will terminate, the postcondition will be true, and 25 the program specification is satisfied

This is an example of the technique known as “theorem proving”, i. e. , we use logic to formally derive results from what we already know To ensure that our results are correct, we need to use an “automated” theorem prover, i. e. , a program that has been shown to use logic correctly and that contains enough rules to allow us to prove the result(s) we need 26