Formal Program Specification Software Testing and Verification Lecture

Formal Program Specification Software Testing and Verification Lecture Notes 16 Prepared by Stephen M. Thebaut, Ph. D. University of Florida

Overview • Review of Basics – Propositions, propositional logic, predicates, predicate calculus – Sets, Relations, and Functions • Specification via pre- and postconditions • Specifications via functions

Propositions, Propositional Logic, Predicates, and the Predicate Calculus

Propositions and Propositional Logic • A proposition, P, is a statement of some alleged fact which must be either true or false, and not both. • Which of the following are propositions? – elephants are mammals – France is in Asia – go away – 5>4 –X>5

Propositions and Propositional Logic (cont’d) • Propositional Logic is a formal language that allows us to reason about propositions. The alphabet of this language is: {P, Q, R, … Л, V, , , ¬} where P, Q, R, … are propositions, and the other symbols, usually referred to as connectives, provide ways in which compound propositions can be built from simpler ones.

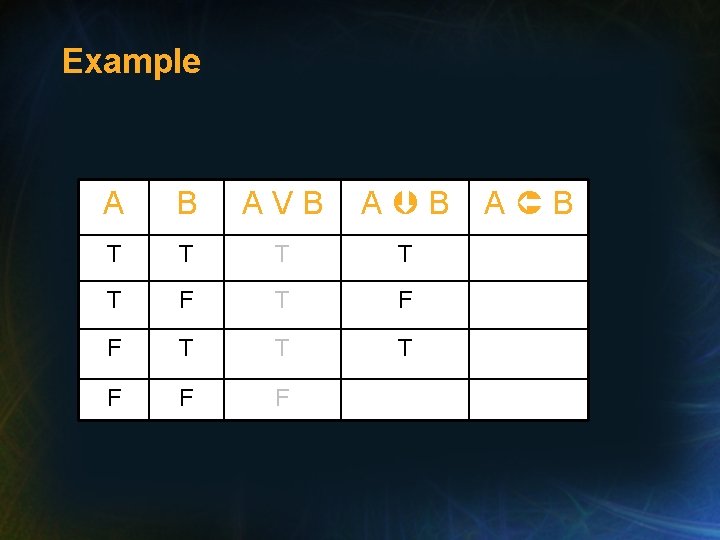
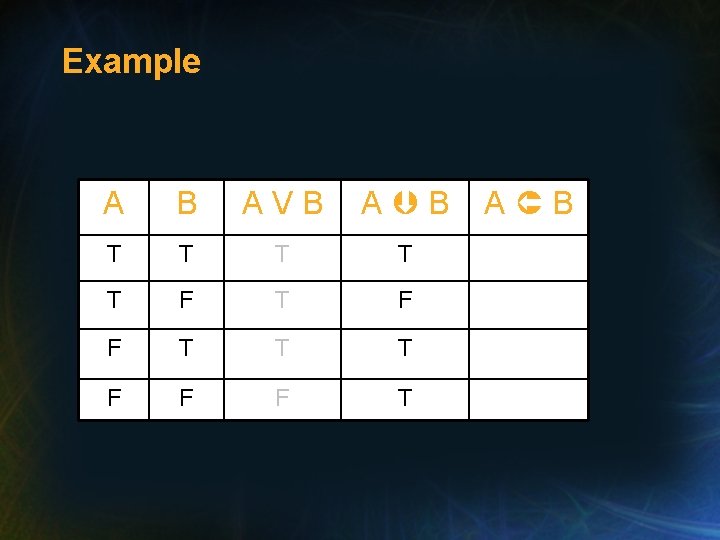
Truth Tables • Truth tables provide a concise way of giving the meaning of compound propositions in a tabular form. Example: construct a truth table to show all possible interpretation for the following sentences: A V B, A B, and A B

Example A B T T T F F AVB A B

Example A B AVB T T F F F A B

Example A B AVB T T F F F A B

Example A B AVB A B T T T F F F A B

Example A B AVB A B T T T F F F A B

Example A B AVB A B T T T F F F A B

Example A B AVB A B T T T F F F T A B

Example A B AVB A B T T T F F F T A B

Example A B AVB A B T T T F T F F F T T T F F T T

Equivalence • Two sentences are said to be equivalent if and only if their truth values are the same under every interpretation. • If A is equivalent to B, we write A B. Exercise: Use a truth table to show: (P Q) (Q V ¬P)

Equivalence (cont’d) • Many users of logic slip into the habit of using and interchangeably. • However, A B is written down in the full knowledge that it may denote either true or false in some interpretation, whereas A B is an expression of “fact” (i. e. , the writer thinks it is true). How would you write A B as an expression of “fact”?

Predicates • Predicates are expressions containing one or more free variables (place holders) that can be filled by suitable objects to create propositions. • For example, instantiating the value 2 for X in the predicate X>5 results in the (false) proposition 2>5.

Predicates (cont’d) • In general, a predicate itself has no truth value; it expresses a property or relation using variables.

Predicates (cont’d) • Two ways in which predicates can give rise to propositions: – As illustrated above, their free variables may be instantiated with the names of specific objects, and – They may be quantified. Quantification introduces two additional symbols: and

Predicates (cont’d) • and are used to represent universal and existential quantification, respectively. – x • duck(x) represents the proposition “every object is a duck. ” – x • duck(x) represents the proposition “there is at least one duck. ”

Predicates (cont’d) • For a predicate with two free variables, quantifying over one of them yields another predicate with one free variable, as in x • Q(x, y) or x • Q(x, y)

Predicates (cont’d) • Where appropriate, a domain of interest may be specified which identifies the objects for which the quantifier applies. For example, i {1, 2, …, N} • A[i]>0 represents the predicate “the first N elements of array A are all greater than 0. ”

Predicate Calculus • The addition of a deductive apparatus gives us a formal system permitting proofs and derivations which we will refer to as the predicate calculus. • The system is based on providing rules of inference for introducing and removing each of the five connective symbols plus the two quantifiers.

Predicate Calculus (cont’d) • A rule of inference is expressed in the form: A 1, A 2, …, An C and is interpreted to mean (A 1 Л A 2 Л … Л An) C So why use a different notation?

Predicate Calculus (cont’d) • Examples of deductive rules: A, B A A AVB ¬¬A A, A B A B (cont’d)

Predicate Calculus (cont’d) • Examples of deductive rules: (cont’d) A B A B, B A A B x • P(x) P(n 1) Л P(n 2) Л … Л P(nk)

Sets, Relations, and Functions

Sets and Relations • A set is any well-defined collection of objects, called members or elements. • The relation of membership between a member, m, and a set, S, is written: m S • If m is not a member of S, we write: m∉S

Sets and Relations (cont’d) • A relation, r, is a set whose members (if any) are all ordered pairs. • The set comprised of the first member of each pair is called the domain of r and is denoted D(r). Members of D(r) are called arguments of r. • The set comprised of the second member of each pair is called the range of r and is denoted R(r). Members of R(r) are called values of r.

Functions • A function, f, is a relation such that for each x D(f) there exists a unique element (x, y) f. • We often express this as y=f(x), where y is the unique value corresponding to x in the function f. • It is the uniqueness of y that distinguishes a function from other relations.

Functions (cont’d) • It is often convenient to define a function by giving its domain and a rule for calculating the corresponding value for each argument in the domain. • For example: f = {(x, y)|x {0, 1}, y = x 2 + 3 x + 2} • This could also be written: f(x) = x 2 + 3 x + 2 where D(f)={0, 1}

Conditional Rules • Conditional rules are a sequence of (predicate rule) pairs separated by vertical bars and enclosed in parentheses: (p 1 r 1 | p 2 r 2 | … | pk rk)

Conditional Rules (cont’d) • The meaning is: evaluate predicates p 1, p 2, …pk in order; for the first predicate, pi, which evaluates to true, if any, use the rule ri; if no predicate evaluates to true, the rule is undefined. (Note that “ ” ≠ “ ”. ) (p 1 r 1 | p 2 r 2 | … | pk rk)

Conditional Rules (cont’d) • For example: f = ((x, y)|(x divisible by 2 y = x/2 | x divisible by 3 y = x/3 | true y = x)) • Note that “true r” has the effect of “if all else fails (i. e. , if all the previous predicates evaluate to false), use r. ”

Recursive Functions • A recursive function is a function that is defined by using the function itself in the rule that defines it. For example: oddeven(x) = (x {0, 1} x | x > 1 oddeven(x-2) | x < 0 oddeven(x+2)) Exercise: define the factorial function recursively.

Specification via Pre- and Post-Conditions

Specification via Pre- and Post. Conditions • The (functional) requirements of a program may be specified by providing: – an explicit predicate on its state before execution (a pre-condition), and – an explicit predicate on its state after execution (a post-condition).

Specification via Pre- and Post. Conditions (cont’d) • Describing the state transition in two parts highlights the distinction between: – the assumptions that an implementer is allowed to make in terms of initial state constraints, and – the obligation that must be met in terms of final state constraints.

Specification via Pre- and Post. Conditions (cont’d) • The language of pre- and post-conditions is that of the predicate calculus. • Predicates denote properties of program variables or relations between them.

Assumptions • Reference to a variable in a predicate implies that it exists and is defined. • Variables are assumed to be of type “integer, ” unless the context of their use implies otherwise. • “A[1: N]” denotes an array with lower index bound of 1 and upper index bound of N (an integer constant).

Example 1 • Consider the pre- and post-conditions for a program that sets variable MAX to the maximum value of two integers, A and B. pre-condition: ? post-condition: ?

Example 1 • Consider the pre- and post-conditions for a program that sets variable MAX to the maximum value of two integers, A and B. pre-condition: ? post-condition: {[(MAX=A Л A B) V (MAX=B Л B A)] Л?

Example 1 • Consider the pre- and post-conditions for a program that sets variable MAX to the maximum value of two integers, A and B. pre-condition: ? post-condition: {[(MAX=A Л A B) V (MAX=B Л B A)] Л A=A’ Л B=B’} (A’ denotes the initial value of variable A. )

Example 1 • Consider the pre- and post-conditions for a program that sets variable MAX to the maximum value of two integers, A and B. pre-condition: {true} post-condition: {[(MAX=A Л A B) V (MAX=B Л B A)] Л A=A’ Л B=B’} (A’ denotes the initial value of variable A. )

Example 2 • Consider the pre- and post-conditions for a program that sets variable MIN to the minimum value in the unsorted, non-empty array A[1: N]. pre-condition: ? post-condition: ?

Example 2 • Consider the pre- and post-conditions for a program that sets variable MIN to the minimum value in the unsorted, non-empty array A[1: N]. pre-condition: ? post-condition: { i {1, 2, …, N} • A[i]=MIN Л

Example 2 • Consider the pre- and post-conditions for a program that sets variable MIN to the minimum value in the unsorted, non-empty array A[1: N]. pre-condition: ? post-condition: { i {1, 2, …, N} • A[i]=MIN Л j {1, 2, …, N} • MIN≤A[j]

Example 2 • Consider the pre- and post-conditions for a program that sets variable MIN to the minimum value in the unsorted, non-empty array A[1: N]. pre-condition: ? post-condition: { i {1, 2, …, N} • A[i]=MIN Л j {1, 2, …, N} • MIN≤A[j] Л A=A ’}

Example 2 • Consider the pre- and post-conditions for a program that sets variable MIN to the minimum value in the unsorted, non-empty array A[1: N]. pre-condition: ? post-condition: { i {1, 2, …, N} • A[i]=MIN Л j {1, 2, …, N} • MIN≤A[j] Л A=A ’}

Example 2 • Consider the pre- and post-conditions for a program that sets variable MIN to the minimum value in the unsorted, non-empty array A[1: N]. pre-condition: {N>0} post-condition: { i {1, 2, …, N} • A[i]=MIN Л j {1, 2, …, N} • MIN≤A[j] Л A=A ’}

Example 2 • Consider the pre- and post-conditions for a program that sets variable MIN to the minimum value in the unsorted, non-empty array A[1: N]. pre-condition: {N>0} post-condition: { i {1, 2, …, N} • A[i]=MIN Л j {1, 2, …, N} • MIN≤A[j] Л A=A ’} What does “unsorted” mean here?

Example 2 (cont’d) • Possible interpretations of “unsorted”: 1. ( i {1, 2, …, N-1} • A[i] A[i+1] V i {1, 2, …, N-1} • A[i] A[i+1]) 2. “the sort operation has not been applied to A” • What was the specifier’s intent? Assume we have determined that (2) was the intent. How can this interpretation be “captured” in a pre-condition?

Example 2 (cont’d) • Consider the pre- and post-conditions for a program that sets variable MIN to the minimum value in the unsorted, non-empty array A[1: N]. pre-condition: {N>0} post-condition: { i∈{1, 2, …, N} • A[i]=MIN Л j∈{1, 2, …, N} • MIN A[j] Л A=A ’}

Specification via Functions

Specification via Functions • Programs may also be specified in terms of intended program functions. • These define explicit mappings from initial to final data states for individual variables and can be expanded into program control structures. • The correctness of an expansion can be determined by considering correctness conditions associated with the control structures relative to the intended function.

Specification via Functions (cont’d) • Data mappings may be specified via the use of a concurrent assignment function. • The domain of the function corresponds to the initial data states that would be transformed into final data states by a suitable program. • For example. . .

Specification via Functions (cont’d) • The conditional function: f = (x 0 Л y 0 x, y : = x+y, 0) specifies a program, say F, for which:

Specification via Functions (cont’d) • The conditional function: f = (x 0 Л y 0 x, y : = x+y, 0) specifies a program, say F, for which: – the final value of x is required to be the sum of the initial values of x and y, and

Specification via Functions (cont’d) • The conditional function: f = (x 0 Л y 0 x, y : = x+y, 0) specifies a program, say F, for which: – the final value of x is required to be the sum of the initial values of x and y, and – the final value of y is required to be 0. . .

Specification via Functions (cont’d) • The conditional function: f = (x 0 Л y 0 x, y : = x+y, 0) specifies a program, say F, for which: – the final value of x is required to be the sum of the initial values of x and y, and – the final value of y is required to be 0. . . …if x and y are both initially 0. Otherwise, F may yield some other result (sufficient correctness) or not terminate (complete correctness) in keeping with f being undefined in this case.

Specification via Functions (cont’d) • Similarly, in a program with data space x, y, z, the sequence of assignment statements: x : = x+1; y : = 2*x computes a function that can be specified by the concurrent assignment function: f = (x, y, z : = x+1, 2(x+1), z) • This function could also be specified using the shorthand notation: f = (x, y : = x+1, 2(x+1)) implying an assignment into that portion of the data space containing x and y, while that containing z is assumed to remain unmodified.

Specification via Functions (cont’d) • In addition, when an intended function is followed by a list of variables surrounded by “#” characters, the intent is to specify a program’s effect on these variables only. Other variables are assumed to receive arbitrary, unspecified values. • For example, consider a program with variables x, y, and temp. The intended function description: f = (x, y : = y, x) #x, y# is equivalent to (x, y, temp : = y, x, ? ) where “? ” represents an arbitrary, unspecified value.

Comparing specification approaches • Pre- and post-conditions for a program with data space x, y, z, temp that is required to swap the values of x and y and leave z unchanged (but has no requirement concerning the disposition of temp): pre-condition: {true} post-condition: {x=y’ Л y=x’ Л z=z’} • Comparable intended function (f 1): f 1 = (x, y : = y, x) #x, y, z# (z is unmodified and temp gets an unspecified value)

Comparing specification approaches (cont’d) • Pre- and post conditions given that the initial values of z and temp can be assumed to be greater that 0: pre-condition: {z>0 Л temp>0} post-condition: {x=y’ Л y=x’ Л z=z’} • Comparable† intended function (f 2): f 2 = (z>0 Л temp>0 x, y : = y, x) #x, y, z# † “Comparable” in the context of sufficient correctness. f 2 is “undefined” when (z>0 Л temp>0) evaluates to false.

Formal Program Specification Software Testing and Verification Lecture Notes 16 Prepared by Stephen M. Thebaut, Ph. D. University of Florida