ICS 253 Discrete Structures I Spring Semester 2014

ICS 253: Discrete Structures I Spring Semester 2014 (2013 -2) Propositional Logic Section 1. 1 Dr. Nasir Al-Darwish Computer Science Department King Fahd University of Petroleum and Minerals darwish@kfupm. edu. sa

Grading l Lecture attendance: -1% per 2 unexcused absences l Assignments & Quizzes: 20% l Two Major Exams: 25% per exam l Final Exam: 30% KFUPM: Dr. Al-Darwish © 2014 1

Expectations l This is really a fun course! l The course covers some of the most useful math you’ll ever learn. l It teaches abstraction, describe (or model) a given problem using precise formal notation Hints for success l Read the textbook. l Lectures really do help! l Do the homework. KFUPM: Dr. Al-Darwish © 2014 2

Propositional Logic l Traditionally, logic distinguishes valid and invalid arguments (2 -valued logic). A claim is either true or false. l There are other types of logic, e. g. fuzzy logic l The building blocks of logic are propositions. l A proposition (claim) is a declarative statement that is either true or false. KFUPM: Dr. Al-Darwish © 2014 3

Propositions versus Not Propositions What’s a proposition? A proposition is a declarative statement that’s either TRUE or FALSE (but not both, not conditional). Propositions Not Propositions 3 + 2 = 32 Bring me coffee! Math is my favorite subject. 3+2 Every cow has 4 legs. Do you like Cake? There is other life in the universe. X – 2 = 10 (depends on X) I will go fishing tomorrow. KFUPM: Dr. Al-Darwish © 2014 4

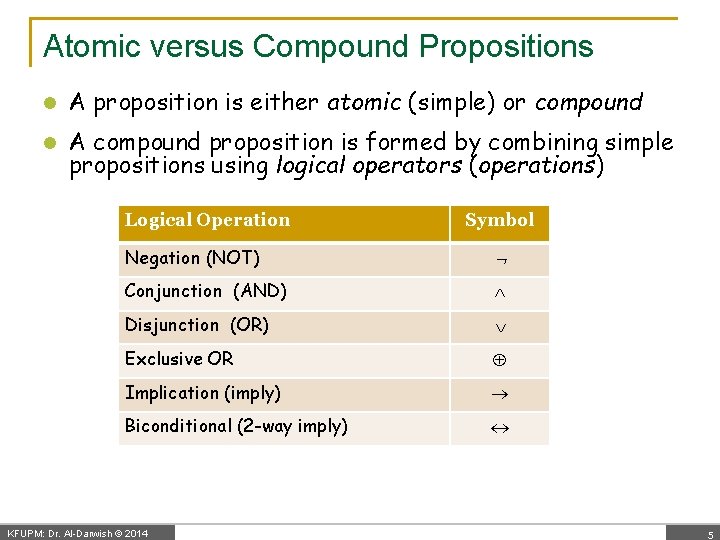
Atomic versus Compound Propositions l A proposition is either atomic (simple) or compound l A compound proposition is formed by combining simple propositions using logical operators (operations) Logical Operation Symbol Negation (NOT) Conjunction (AND) Disjunction (OR) Exclusive OR Implication (imply) Biconditional (2 -way imply) KFUPM: Dr. Al-Darwish © 2014 5

Logical Operations l Let p & q be propositions, then the following are compound propositions: l Negation: p = not p l Conjunction: p q = p AND q l Disjunction: l Exclusive OR: l Implication: p q = if p then q l Biconditional: p q = p if and only if q KFUPM: Dr. Al-Darwish © 2014 p q = p OR q = p XOR q 6

Precedence of Logical Operators n In a parenthesized expression, the inner most parenthesized part is computed first n Binary operators with same precedence are applied left-to-right; unary are applied right-to-left n The following is the order of operators by precedence , , v , , q This means for example (assuming parenthesis are not present) (((p ( q)) v p v q) ((p ( q)) v p) KFUPM: Dr. Al-Darwish © 2014 7

Truth Tables l A truth table shows the truth values of a compound proposition in relation to the truth values of its constituent propositions l Normally, the truth table will have as many rows as the different possible truth value of its constituent propositions. For example, a compound proposition involving two simple propositions P, Q will have 4 rows (4 different T/F combinations for P and Q). KFUPM: Dr. Al-Darwish © 2014 8

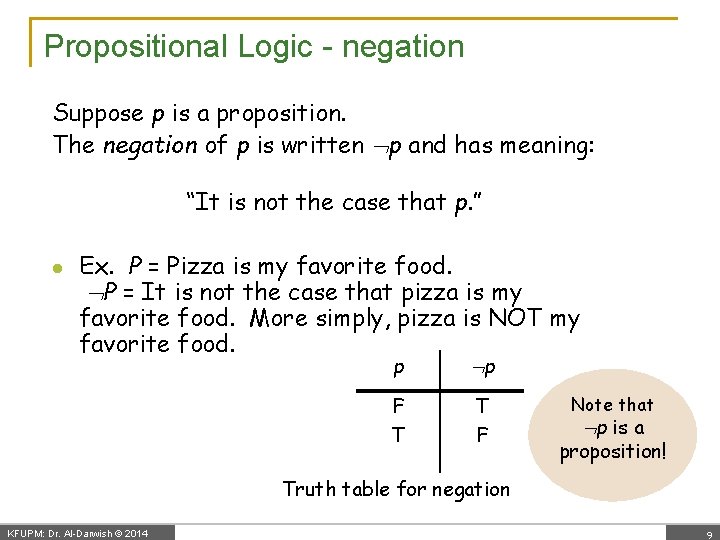
Propositional Logic - negation Suppose p is a proposition. The negation of p is written p and has meaning: “It is not the case that p. ” l Ex. P = Pizza is my favorite food. P = It is not the case that pizza is my favorite food. More simply, pizza is NOT my favorite food. p p F T T F Note that p is a proposition! Truth table for negation KFUPM: Dr. Al-Darwish © 2014 9

Propositional Logic - conjunction Conjunction corresponds to English “and” p q is true exactly when p is true and q is true (or both are true). l Ex. Amy is curious AND clever. p q F F T T F T F F F T Truth table for conjunction KFUPM: Dr. Al-Darwish © 2014 10

Propositional Logic - disjunction Disjunction corresponds to English “or” p q is true when p is true or q is true (or both are true). l Ex. Michael is brave OR nuts. p q F F T T F T F T Truth table for disjunction KFUPM: Dr. Al-Darwish © 2014 11

The implication p q corresponds to English: “if p then q” or “p implies q” l P Q can be considered as a contract that relates a condition P to a conclusion Q l P = build me a house, Q = pay you $1 million l If you build me a house then I will pay you $1 million l l l The contract is violated if the house is built but the payment is not made p q p q is false only in the case where p is true and q is false If p then 2+2=4. (This is true. Why? ) F F T T F T p q T T F T Truth table for implication KFUPM: Dr. Al-Darwish © 2014 12

Propositional Logic - logical equivalence How many different logical binary operations could we define? How many different logical operations do we need? 16 ? ? To answer, we need the notion of “logical equivalence. ” p is logically equivalent to q if their truth tables are the same. Logical equivalence is denoted by p q (or p q). KFUPM: Dr. Al-Darwish © 2014 13

Propositional Logic - logical equivalence Challenge: Try to find a proposition that is equivalent to p q, but that uses only the connectives , , and . p q p q p p q F F T T F T T T F F T T F T KFUPM: Dr. Al-Darwish © 2014 14

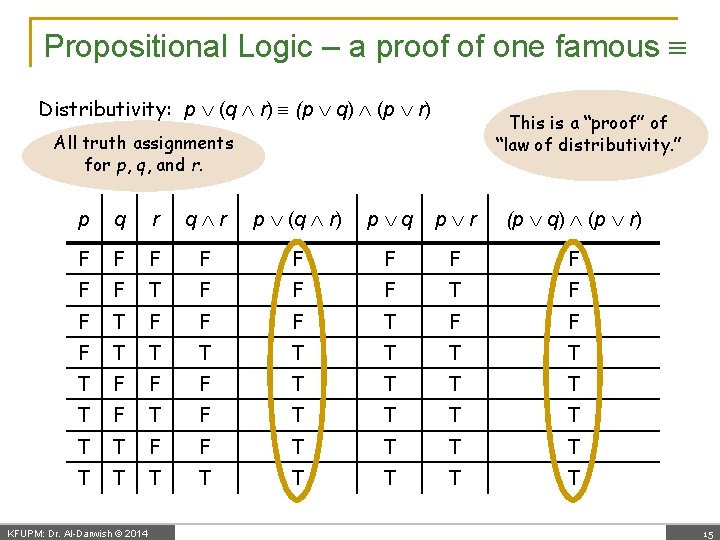
Propositional Logic – a proof of one famous Distributivity: p (q r) (p q) (p r) This is a “proof” of “law of distributivity. ” All truth assignments for p, q, and r. p q r p (q r) p q p r (p q) (p r) F F F F F T F F F T T T T F F F T T T F F T T T KFUPM: Dr. Al-Darwish © 2014 15

Expressing Implications The implication p q essentially says that we cannot have p true yet q is false, (p q). Thus, p q (p q) (1). (The equivalence can be shown by truth table) Simplifying the RHS (use De. Morgan’s law) , gives p q (2) It is important to observe that p q also means (because we cannot have p and not q): not q not p It is easy to show that p q q p (3) This last equivalence is known as the Contra. Positive (negative of positive). I liken it to “the cub is half full the cub is half empty” KFUPM: Dr. Al-Darwish © 2014 16

Expressing Implications – cont. Definition: p is sufficient for q if whenever p is true, q is true. Thus, p q means that p is sufficient for q. Definition: p is necessary for q if whenever p is false, q is false. Thus, p q means that q is necessary for q. (recall from previous slide that p q q p) KFUPM: Dr. Al-Darwish © 2014 17

Expressing Implications – cont. The following are some of the ways of expressing p q l p implies q l if p then q l if p, q l q if p (stating the conclusion first) l p only if q* (see next two slides for justification) l p is sufficient for q l q is necessary for p l q whenever (when) p l q follows from p l q unless ¬p* ** These seem confusing KFUPM: Dr. Al-Darwish © 2014 18

Expressing Implications – cont. p q can be expressed as: l l p only if q: l p cannot be true if q is not true l This corresponds to the contrapositive of p q q unless p l If p is false, then q must be true l Example: l If You fail the final exam then you will get F l You will get F unless you do not fail the final exam KFUPM: Dr. Al-Darwish © 2014 19

Propositional Logic - biconditional The biconditional proposition p ↔ q (read as, p if and only if q) states that p and q are always equal (either they are both true or both false) The biconditional proposition p ↔ q is equivalent to “(p q) and (q p)” Because in the expression “p if and only if q” , “p if q” is q p, it follows that p q is “p only if q” p q p↔q F F T T F F T Truth table for biconditional Question: Is p ↔ q (p q) ( p q)? KFUPM: Dr. Al-Darwish © 2014 20

Propositional Logic - some definitions Contrapositives: p q and q p l Ex. “If it is noon, then I am hungry. ” Note: p q q p “If I am not hungry, then it is not noon. ” Converses: p q and q p l Ex. “If it is noon, then I am hungry. ” “If I am hungry, then it is noon. ” Inverses: p q and p q l Ex. “If it is noon, then I am hungry. ” “If it is not noon, then I am not hungry. ” KFUPM: Dr. Al-Darwish © 2014 21

Propositional Logic - more definitions… A tautology is a proposition that’s always TRUE. A contradiction is a proposition that’s always FALSE. p p T F F T T F KFUPM: Dr. Al-Darwish © 2014 22

Translating English Sentences n English (and every other human language) is often ambiguous. Translating sentences into compound propositions removes the ambiguity. n Example: How can this English sentence be translated into a logical expression? “You can access the Internet from campus only if you are a computer science major or you are not a freshman. ” Solution: Let a, c, and f represent “You can access the Internet from campus”, “You are a computer science major”, and “You are a freshman” The sentence can be translated into: a → (c ν ¬f). KFUPM: Dr. Al-Darwish © 2014 23

Translating English Sentences n Example: How can this English sentence be translated into a logical expression? “You cannot enter into the pool if you are under 4 feet tall unless you are older than 16 years old. ” Solution: Let p, r, and s represent “You can enter into the pool” , “You are under 4 feet tall”, and “You are older than 16 years old” The sentence can be translated into: (r Λ ¬ s) → ¬p. KFUPM: Dr. Al-Darwish © 2014 24

Propositional Logic – why? … We’re primarily using propositional logic as a foundation formal proofs. Later we will study different proof methods and these are needed for developing (or ensuring correctness) of algorithms. Propositional logic is a key to writing correct program code…you can’t do any kind of conditional (if) statement without understanding the condition you’re testing. The logical operations we’ve discussed are also found in hardware and are called “logic gates. ” KFUPM: Dr. Al-Darwish © 2014 25