ICS 253 Discrete Structures I Spring Semester 2014

ICS 253: Discrete Structures I Spring Semester 2014 (2013 -2) Propositional Logical Equivalence Dr. Nasir Al-Darwish Computer Science Department King Fahd University of Petroleum and Minerals darwish@kfupm. edu. sa

Tautologies, contradictions, contingencies n A compound proposition is a tautology if it is always true no matter what truth values its atomic propositions have. q n The opposite to a tautology, is a compound proposition that’s always false – a contradiction. q n Example: p ¬p On the other hand, a compound proposition whose truth value isn’t constant is called a contingency. q Example: p ¬p KFUPM: Dr. Al-Darwish © 2014 1

Tautologies and contradictions The easiest way to see if a compound proposition is a tautology or a contradiction is to use a truth table. KFUPM: Dr. Al-Darwish © 2014 2

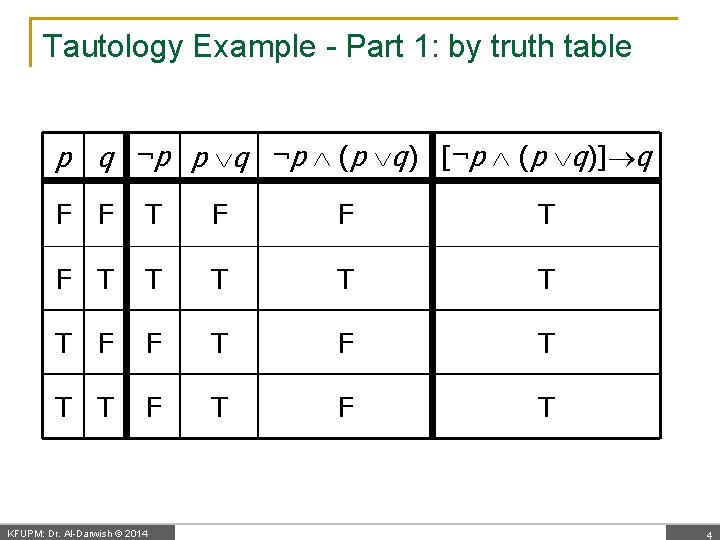
Tautology Example Demonstrate that [¬p (p q)] q is a tautology in two ways: 1. Using a truth table – show that [¬p (p q)] q is always true 2. Using a proof (will get to this later). Note: The LHS asserts (states) two facts: ¬p and (p q) Clearly, these assertions taken together imply q. KFUPM: Dr. Al-Darwish © 2014 3

Tautology Example - Part 1: by truth table p q ¬p (p q) [¬p (p q)] q F F T F T T T F T KFUPM: Dr. Al-Darwish © 2014 4

Tautologies, contradictions and programming Tautologies and contradictions in your code usually correspond to poor programming design. Examples: n n while(x <= 3 || x > 3) x++; if(x > y) if(x == y) return “never got here”; KFUPM: Dr. Al-Darwish © 2014 5

Logical Equivalence n Definition: Two compound propositions p, q are logically equivalent if their truth tables are the same. n Alternative Definition: Two compound propositions p, q are logically equivalent if their biconditional joining p q is a tautology. n Logical equivalence is denoted by p q or p q. q Example: A logical implication is equivalent to its contrapositive. That is, p q ¬q ¬p. KFUPM: Dr. Al-Darwish © 2014 6

Logical Equivalence - Example 1 The easiest way to test for logical equivalence is to check if the truth tables of both propositions have identical last columns Example: Is p q ¬q ¬p? p q p q T T F F T F T T T T F F T F ¬q F T ¬p F F T T ¬q ¬p T F T T Note that because the last columns are identical, it follows that (p q) (¬q ¬p) is a tautology, which is consistent with the second def. of equivalence in previous slide. KFUPM: Dr. Al-Darwish © 2014 7

Logical Equivalence - Example 2 n Show that ┐(p v q) and ┐p ˄ ┐ q are equivalent KFUPM: Dr. Al-Darwish © 2014 8

Logical Non-Equivalence of Conditional and Converse The converse of a logical implication is the reversal of the implication. I. e. the converse of p q is q p. Example: The converse of “If Donald is a duck then Donald is a bird. ” is “If Donald is a bird then Donald is a duck. ” As we’ll see next: p q and q p are not logically equivalent. KFUPM: Dr. Al-Darwish © 2014 9

Logical Non-Equivalence of Conditional and Converse p q T T F F T F p q q p T F T (p q) ( q p) T F F T Note that because the columns for p q and q p are not identical, we can immediately conclude that these propositions are not equivalent. KFUPM: Dr. Al-Darwish © 2014 10

Derivational Proof Techniques When a compound proposition involves many atomic components, the size of the truth table for the compound proposition becomes large Q 1: How many rows are required to construct the truth-table of: ((q (p r )) ( (s r) t) ) ( q r) ? Q 2: How many rows are required to construct the truth-table of a proposition involving n atomic components? A 1: 32 rows, each additional variable doubles the number of rows A 2: In general, 2 n rows Therefore, as compound propositions grow in complexity, truth tables become more and more unwieldy. In such cases, it is better to use derivational proof techniques KFUPM: Dr. Al-Darwish © 2014 11

Derivational Proof Techniques Example: consider the compound proposition (p p ) ( (s r) t) ) ( q r ) Q: Why is this a tautology? KFUPM: Dr. Al-Darwish © 2014 12

Derivational Proof Techniques Answer: The part (p p) is a tautology and the disjunction (or) of True with any other compound proposition always results in True: (p p ) ( (s r) t )) ( q r ) T ( (s r) t )) ( q r ) T Derivational techniques formalize the intuition of this example. KFUPM: Dr. Al-Darwish © 2014 13

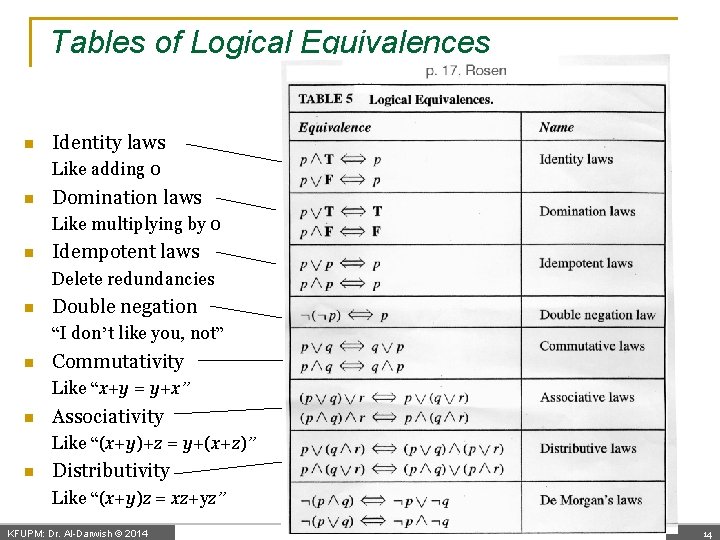
Tables of Logical Equivalences n Identity laws Like adding 0 n Domination laws Like multiplying by 0 n Idempotent laws Delete redundancies n Double negation “I don’t like you, not” n Commutativity Like “x+y = y+x” n Associativity Like “(x+y)+z = y+(x+z)” n Distributivity Like “(x+y)z = xz+yz” KFUPM: Dr. Al-Darwish © 2014 14 14

Tables of Logical Equivalences n n n Excluded middle Negating creates opposite Definition of implication in terms of Not and Or KFUPM: Dr. Al-Darwish © 2014 15

De. Morgan Identities De. Morgan’s identities allow for simplification of negations of complex expressions n Conjunctional negation: (p 1 p 2 … pn) ( p 1 p 2 … pn) “It’s not the case that all are true iff one is false. ” n Disjunctional negation: (p 1 p 2 … pn) ( p 1 p 2 … pn) “It’s not the case that one is true iff all are false. ” KFUPM: Dr. Al-Darwish © 2014 16

Tautology Example - Part 2 Demonstrate that [¬p (p q )] q is a tautology in two ways: 1. Using a truth table (was done previously) 2. Using a proof relying on Tables 5 and 6 of Rosen, section 1. 3 to derive True through a series of logical equivalences KFUPM: Dr. Al-Darwish © 2014 17

Tautology by proof [¬p (p q )] q [(¬p p) (¬p q)] q Distributive [ F (¬p q)] q ULE [¬p q ] q Identity ¬ [¬p q ] q ULE [¬(¬p) ¬q ] q De. Morgan [p ¬q ] q Double Negation p [¬q q ] Associative p [q ¬q ] Commutative p T ULE T Domination KFUPM: Dr. Al-Darwish © 2014 18

Important Equivalences 1. p q (p q) // meaning of 2. p q 3. p q q p 4. (p q) p q // negation of 1 5. (p q) (p r) p (q r) 6. (p q) (p r) p (q r) 7. (p r) (q r) (p q) r 8. (p r) (q r) (p q) r 9. p q (p q) (q p) 10. (p q) p q KFUPM: Dr. Al-Darwish © 2014 // simplify RHS of 1 // contrapositive 19