I Radicali Definizione e caratteristiche Dato un numero






















- Slides: 27

I Radicali Definizione e caratteristiche Dato un numero reale non negativo a ed un numero intero positivo n, esiste uno ed un solo numero reale non negativo b tale che bn = a. Il numero b si dice radice n-esima assoluta di a ed in simboli si scrive Il simbolo (con n ≥ 2) prende il nome di radicale, a è l’argomento del radicale o radicando, il numero n è l’indice del radicale, il numero è la radice n-esima di a. indice Se a si può esprimere come potenza, cioè se il radicale si può esprimere nella forma , il numero pm è il radicando e m si dice esponente del radicando. 3 √ 64 esponente del radicando 1

I Radicali Definizione e caratteristiche • Dalla definizione si ha che ESEMPIO • Un radicale di indice 2 è un radicale quadratico. : radice quadrata di a L’indice 2 può essere omesso: • Un radicale di indice 3 è un radicale cubico. : radice cubica di a ESEMPI è un radicale quadratico è un radicale cubico 2

I Radicali Proprietà invariantiva Il radicale che si ottiene moltiplicando l’indice della radice e l’esponente del radicando per uno stesso numero intero positivo ha lo stesso valore del radicale dato; in simboli: ESEMPIO Grazie a questa proprietà si possono definire le seguenti operazioni: • semplificazione di radicali • moltiplicazione e divisione tra radicali • portar dentro o portar fuori dal simbolo di radice i possibili fattori 3

I Radicali Semplificazione La semplificazione di un radicale Se in un radicale l’indice della radice e l’esponente del radicando hanno un fattore comune, il radicale che si ottiene dividendoli per tale fattore ha lo stesso valore di quello dato; in simboli: ESEMPI 3 2 Radicale irriducibile: radicale in cui l’indice della radice e l’esponente del radicando non hanno fattori comuni. Per ottenere con la semplificazione un radicale irriducibile basta dividere l’indice e l’esponente del radicando per il loro M. C. D. ESEMPIO 4

I Radicali Semplificazione La semplificazione e il valore assoluto Nella definizione di radicale abbiamo richiesto che il radicando sia positivo o nullo. Se il radicando contiene una o più lettere dobbiamo porre le condizioni di non negatività. ESEMPIO Ha significato solo se x – 1 ≥ 0, cioè per x ≥ 1 Nella semplificazione di radicali con radicando letterale a volte si ottiene come risultato un radicale che ha significato per valori delle variabili diverso da quello di partenza. ESEMPIO definito in R definito per 2 x + 1 ≥ 0 x≥− 1 2 Per mantenere l’uguaglianza occorre rendere positiva l’espressione 2 x + 1 utilizzando l’operatore valore assoluto. 5

I Radicali Proprietà Ricordiamo la definizione di valore assoluto di un numero: a se a >0 −a se a <0 |a|= Quindi: ESEMPIO 6

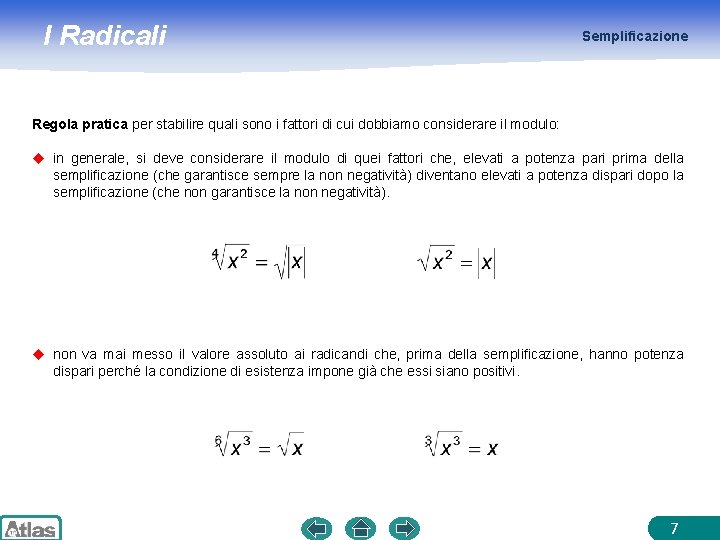
I Radicali Semplificazione Regola pratica per stabilire quali sono i fattori di cui dobbiamo considerare il modulo: u in generale, si deve considerare il modulo di quei fattori che, elevati a potenza pari prima della semplificazione (che garantisce sempre la non negatività) diventano elevati a potenza dispari dopo la semplificazione (che non garantisce la non negatività). u non va mai messo il valore assoluto ai radicandi che, prima della semplificazione, hanno potenza dispari perché la condizione di esistenza impone già che essi siano positivi. 7

I Radicali Operazioni con i radicali quadratici con a Forma del radicale quadratico: >0 Prodotto e quoziente di radicali quadratici Teorema. Il prodotto o il quoziente di due radicali quadratici è un radicale quadratico che ha come radicando rispettivamente il prodotto e il quoziente dei radicandi: con a, b≥ 0 con a ≥ 0, b > 0 ESEMPIO 8

I Radicali Operazioni con i radicali quadratici Elevamento a potenza di radicali quadratici Per elevare a potenza n-esima un radicale quadratico, si eleva a quella potenza il radicando: ESEMPIO 9

I Radicali Operazioni con i radicali quadratici Il trasporto dentro e fuori il simbolo di radice Per trasportare un fattore esterno a sotto il simbolo di radice quadrata ci si comporta così: • se a ≥ 0 si eleva a al quadrato e si lascia il segno positivo all’esterno: • se a < 0 si trasforma a in −(−a), si eleva −a al quadrato e si lascia il segno negativo all’esterno: ESEMPI se x≥ 0 se x<0 10

I Radicali Operazioni con i radicali quadratici Per trasportare un fattore fuori dal simbolo di radice quadrata ci si comporta così: con a dato il radicale ≥ 0 e m > 2, se indichiamo con: • q il quoziente intero della divisione di m per l’indice della radice (nel caso di radicali quadratici m : 2) • r il resto di tale divisione vale la seguente relazione ESEMPIO quoziente 3 7: 2 quindi resto esponente 1 indice 11

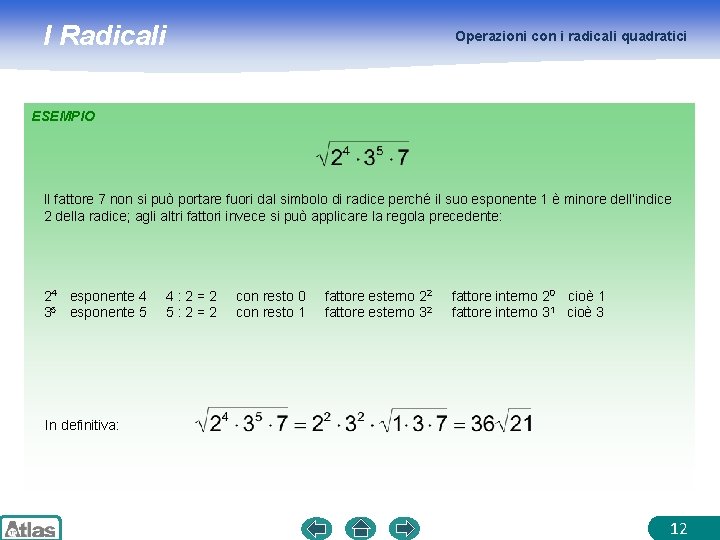
I Radicali Operazioni con i radicali quadratici ESEMPIO Il fattore 7 non si può portare fuori dal simbolo di radice perché il suo esponente 1 è minore dell’indice 2 della radice; agli altri fattori invece si può applicare la regola precedente: 24 esponente 4 35 esponente 5 4: 2=2 5: 2=2 con resto 0 con resto 1 fattore esterno 2 2 fattore esterno 3 2 fattore interno 20 cioè 1 fattore interno 31 cioè 3 In definitiva: 12

I Radicali Operazioni con i radicali quadratici Addizione e sottrazione Infatti: mentre L’addizione e la sottrazione tra più radicali dà come risultato un unico radicale solo nel caso di radicali simili. ESEMPI Sono simili i radicali perché hanno la stessa parte radicale. 13

I Radicali cubici e operazioni con i radicali cubici Forma del radicale cubico: vale l’uguaglianza con a >0 Un segno negativo all’interno di un radicale cubico può essere trasportato all’esterno. Operazioni con i radicali cubici • Prodotto e quoziente: ESEMPIO 14

I Radicali Operazioni con i radicali cubici • Potenza: ESEMPIO • Trasporto sotto al simbolo di radice Si eleva al cubo il valore assoluto del fattore esterno lasciando fuori il segno. ESEMPIO 15

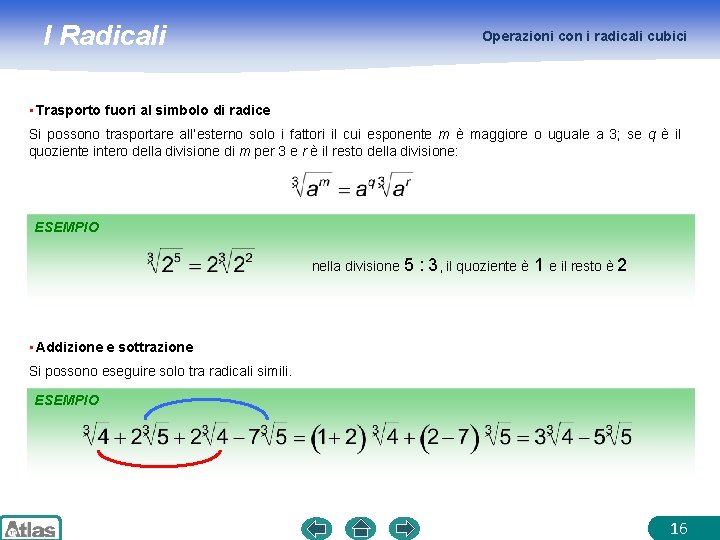
I Radicali Operazioni con i radicali cubici • Trasporto fuori al simbolo di radice Si possono trasportare all’esterno solo i fattori il cui esponente m è maggiore o uguale a 3; se q è il quoziente intero della divisione di m per 3 e r è il resto della divisione: ESEMPIO nella divisione 5 : 3, il quoziente è 1 e il resto è 2 • Addizione e sottrazione Si possono eseguire solo tra radicali simili. ESEMPIO 16

I Radicali Operazioni con i radicali di indice n qualsiasi Le operazioni che abbiamo imparato ad eseguire tra radicali quadratici e cubici si possono eseguire tra radicali di indice n qualsiasi con le stesse regole già enunciate tenendo presente che: • prodotti e quozienti di radicali si possono eseguire solo tra radicali aventi lo stesso indice; in questo caso: • per elevare a potenza un radicale si eleva a quella potenza il radicando: • un fattore positivo si può trasportare sotto il simbolo di radice elevandolo a potenza n: • un fattore si può trasportare fuori dal simbolo di radice solo se il suo esponente è maggiore o uguale all’indice della radice, ed è: con q quoziente intero della divisione m: n e r resto della divisione. • somme e differenze di radicali si possono eseguire solo tra radicali simili. 17

I Radicali Operazioni con i radicali di indice n qualsiasi ESEMPI 18

I Radicali Operazioni con i radicali di indice n qualsiasi Nel caso di radicali di indici diversi la procedura per eseguire il prodotto o il quoziente è la seguente: • si riducono i radicali allo stesso indice, che è il m. c. m. tra gli indici delle radici • si esegue il prodotto o il quoziente • si semplifica, se possibile, il radicale ottenuto. Per ridurre i radicali allo stesso indice si applica la proprietà invariantiva. ESEMPIO Scomponiamo innanzi tutto i radicali e vediamo se è possibile semplificarli: Le tre radici hanno rispettivamente indice 2, 6, 3, quindi l’indice comune è 6: 19

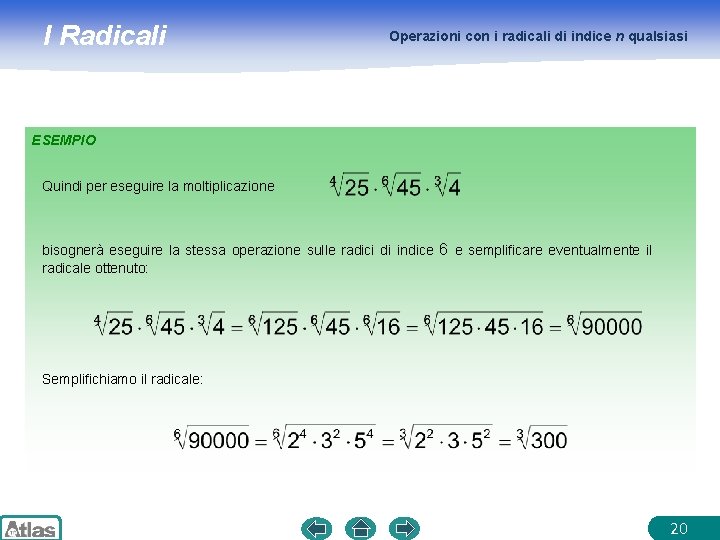
I Radicali Operazioni con i radicali di indice n qualsiasi ESEMPIO Quindi per eseguire la moltiplicazione bisognerà eseguire la stessa operazione sulle radici di indice 6 e semplificare eventualmente il radicale ottenuto: Semplifichiamo il radicale: 20

I Radicali Radice di radicale con a ≥ 0 ESEMPI e semplificando il radicale 21

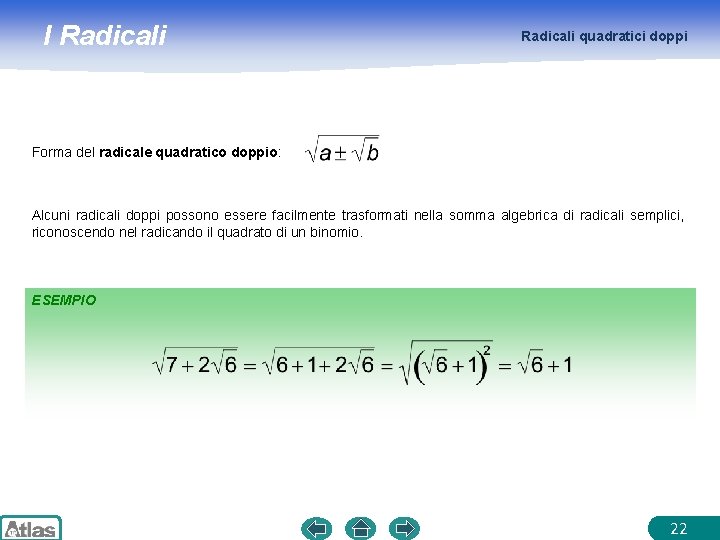
I Radicali quadratici doppi Forma del radicale quadratico doppio: Alcuni radicali doppi possono essere facilmente trasformati nella somma algebrica di radicali semplici, riconoscendo nel radicando il quadrato di un binomio. ESEMPIO 22

I Radicali quadratici doppi In alternativa, se a 2 – b è un quadrato perfetto, si può usare la formula: ESEMPIO Calcoliamo a 2 – b = 144 – 63 = 81 = 92 23

I Radicali Razionalizzazione Razionalizzare il denominatore di una frazione significa trasformare la frazione in un’altra equivalente che abbia denominatore razionale. La trasformazione viene effettuata applicando la proprietà invariantiva della divisione, moltiplicando numeratore e denominatore per un opportuno fattore razionale, detto fattore razionalizzante. • Frazioni del tipo ; il fattore razionalizzante è ESEMPIO • Frazioni del tipo ; con k < 3 il fattore razionalizzante è ESEMPIO 24

I Radicali Frazioni del tipo Razionalizzazione ; il fattore razionalizzante è ESEMPIO Frazioni del tipo ; il fattore razionalizzante è ESEMPIO 25

I Radicali Potenze ad esponente razionale Se a ≥ 0 e m, n sono interi positivi, allora: Il denominatore n della frazione dell’esponente diventa l’indice della radice. Il numeratore m diventa l’esponente del radicando. ESEMPI Se l’esponente è un numero negativo, occorre prima invertire la base: 26

I Radicali Potenze ad esponente razionale Per le potenze ad esponente razionale valgono le seguenti proprietà che derivano dalle consuete proprietà delle potenze: u. am/n ap/q = am/n + p/q u. am/n : ap/q = am/n − p/q u. (a b)m/n = am/n bm/n u. (a : b)m/n = am/n : bm/n u. (am/n)p/q = amp/nq ESEMPIO 27
 Definizione radicali
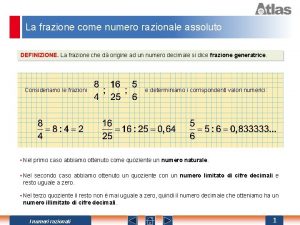
Definizione radicali Frazione che origina un numero razionale
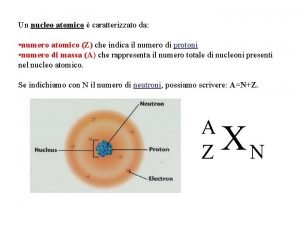
Frazione che origina un numero razionale Numero di ossidazione definizione
Numero di ossidazione definizione Erwin schrödinger modelo atomico
Erwin schrödinger modelo atomico Las pilas de cajas deben estar organizadas
Las pilas de cajas deben estar organizadas Un dato importante
Un dato importante Pemimpin tempatan menentang british
Pemimpin tempatan menentang british Dato t
Dato t Datos objetivos y subjetivos
Datos objetivos y subjetivos Invariante di rappresentazione
Invariante di rappresentazione Dato curioso del calamar
Dato curioso del calamar Azman shah dato aziz
Azman shah dato aziz Pemimpin tempatan
Pemimpin tempatan Dxn pv report
Dxn pv report Smkdi
Smkdi Datos curiosos sobre el alcohol
Datos curiosos sobre el alcohol Sted og dato
Sted og dato Tipos de variables dependientes
Tipos de variables dependientes Ea technique share price
Ea technique share price Dato il segmento ab di lunghezza unitaria
Dato il segmento ab di lunghezza unitaria Peta larut matang dan selama
Peta larut matang dan selama Dato raymond liew
Dato raymond liew Peta kawasan penentangan dato maharaja lela
Peta kawasan penentangan dato maharaja lela Long tipo de dato
Long tipo de dato Pegawai daerah kuala pilah
Pegawai daerah kuala pilah Dato’ dr mansor fadzil
Dato’ dr mansor fadzil Radicale algebrico e aritmetico
Radicale algebrico e aritmetico Radicali liberi matematica
Radicali liberi matematica