How to Draw a Tree LSystems in Computer

How to Draw a Tree L-Systems in Computer Graphics Steven Janke

Natural Trees

Tree Shapes

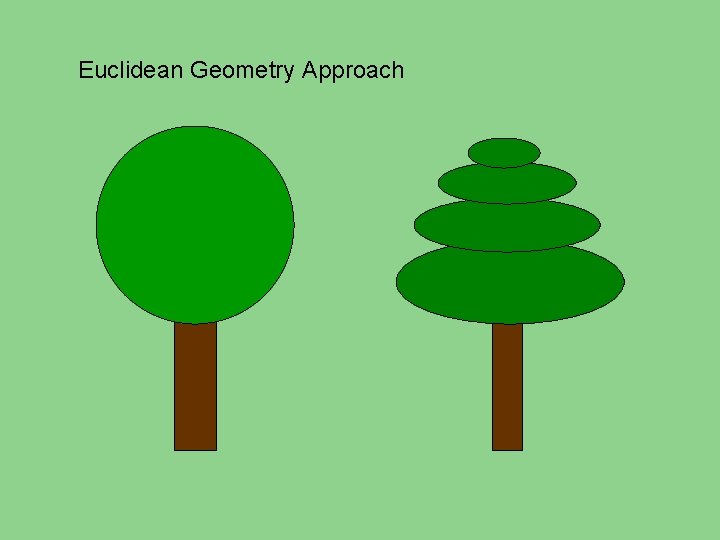
Euclidean Geometry Approach

Self-Similarity of Organic Forms

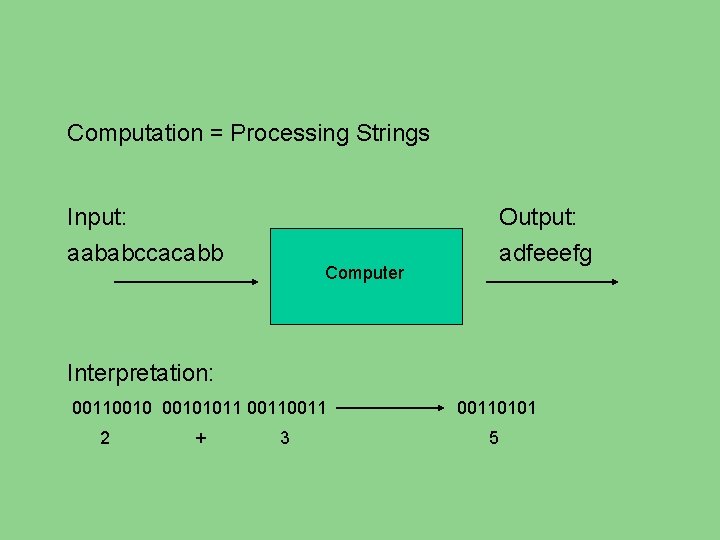
Computation = Processing Strings Input: aababccacabb Computer Output: adfeeefg Interpretation: 001100101011 0011 2 + 3 00110101 5

L-System (Named after biologist Astrid Lindemayer in 1970’s) § Alphabet of characters. § First string called the axiom. § Set of productions showing how to replace characters. § All appropriate productions applied at once. Example: Alphabet: {a, b} Axiom: ab Productions: a bab , Derivation: ab baba b a abab

Languages: L(G) = set of strings that can be derived from the system G. Example 1: Axiom: ab ab aab Productions: a aaab a b aaaab ab L(G) = { an b | n > 0 } Example 2: Axiom: a a b L(G) = ? Productions: a ab b abbab bababbab

Languages: L(G) = set of strings that can be derived from the system G. Example 1: Axiom: ab ab aab Productions: a aaab a b aaaab ab L(G) = { an b | n > 0 } Example 2: Axiom: a a b Productions: a ab b abbab L(G) = { s | s 0 = a, s 1 = b, sn = sn-2 sn-1 } b ab bababbab

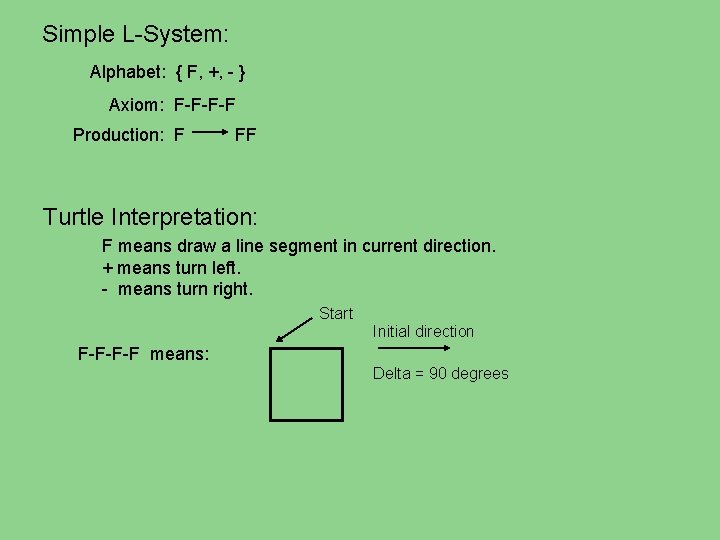
Simple L-System: Alphabet: { F, +, - } Axiom: F-F-F-F Production: F FF Turtle Interpretation: F means draw a line segment in current direction. + means turn left. - means turn right. Start Initial direction F-F-F-F means: Delta = 90 degrees

Branching L-Systems: Add two characters to alphabet: [ and ] Interpret [ to mean “start branch”. Interpret ] to mean “end branch”. F[+F][-F] means: Initial Direction Start Delta = 45 degrees

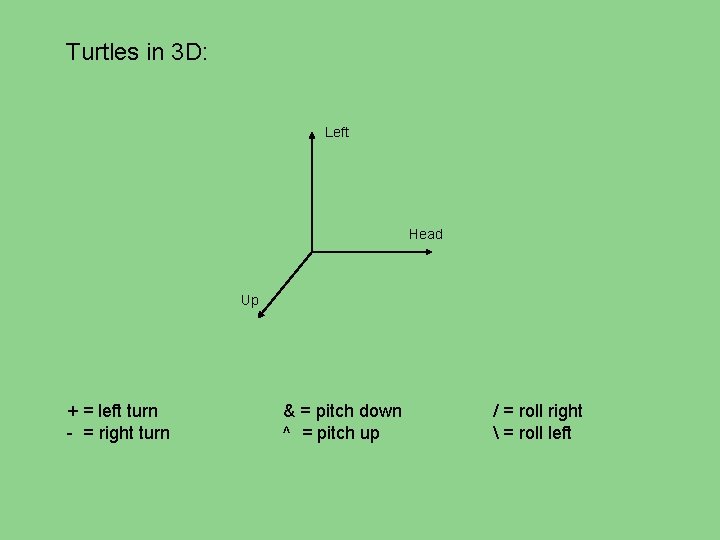
Turtles in 3 D: Left Head Up + = left turn - = right turn & = pitch down ^ = pitch up / = roll right = roll left

Growth Functions: F(k) = length of the kth word in the derivation sequence. Example: a aa F(k) = 2 k Axiom: a a abcc 1 4 b bcc c abccbcccc 9 c Axiom: a abccbcccccc 16 F(k) = k 2 F (

Growth Functions: G: a b b ab Axiom: b ak = number of a’s at iteration k. bk = number of b’s at iteration k. 0 1 1 ak 1 bk ak+1 = bk+1 Theorem: Every growth function for an L-system is a linear combination of terms that are polynomials times exponential functions. Problem: Plants usually grow according to a logistic (or sigmoidal) function.

Parametric L-Systems: Axiom: A(3) A(x) : x<5 B(y) : * B(x+1)A(x*r) F(y)[+F(y/2)][-F(y/2)] Interpretation: F(x) means draw a segment of length x. +(x) means turn left x degrees.

Context Sensitive L-Systems Axiom: SFFFFA Production: SF SFFFFA FS FSFFFA SA B FFSFFA FFFSFA FFFFSA Axiom: S[FA][FFA] [FSA][FSFA] [FB][FFSA] [FB][FFB] FFFFB

Developmental model using signals:

L-System Extensions: § Gravity - pull on branches. § Phyllotaxis - angle and position of branches. § Phototropism - towards the light. § Self-Organizing - branch into free spaces. Implementation: At each iteration, interpret the string and then decide based on the geometry and environment how to apply productions for the next iteration.

Colonization Algorithm: (Runions, Lane, and Prusinkiewicz 2007)

Colonization Algorithm:

Self-Organization Algorithm: (Palubicki 2009)

Self-Organization Algorithm:

Equivalence: G 1 : a bb b a G 2 : a a b b b a Axiom: b aa aa aa bbbb Axiom: a bb aaaa L(G 1) = L(G 2) Is there an algorithm for determining if two L-Systems are equivalent?

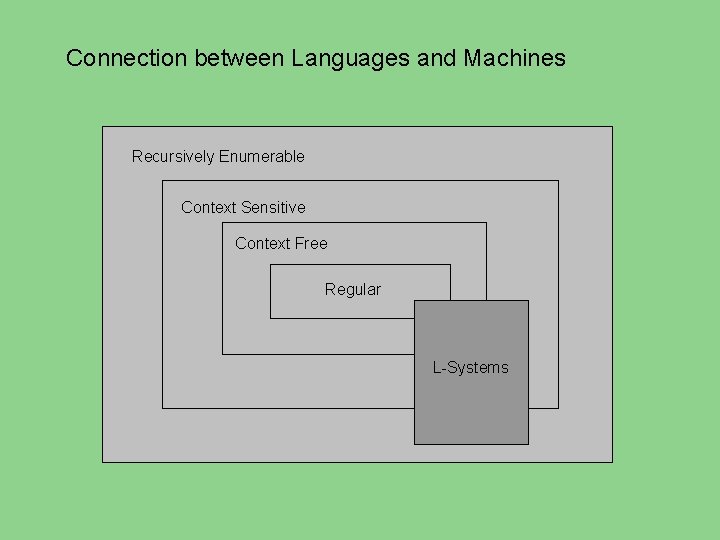
Connection between Languages and Machines Recursively Enumerable Context Sensitive Context Free Regular L-Systems

Iterated Function System: