Tree 1 Tree Definitions 2 Binary Tree Traversals


Tree 1. Tree Definitions 2. Binary Tree – Traversals – Binary Search Tree – Representations – Application : Expression Tree รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ 3. 4. AVL Tree Which Representions ? 5. n-ary Tree 6. Generic Tree 7. Multiway Search Tree 8. B-Trees KMITL 01076249 Data Structures & Algorithms : Tre 2
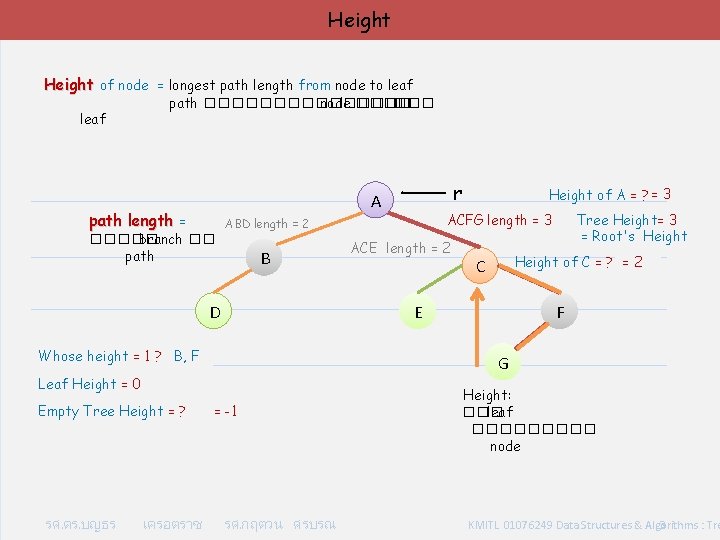
Height of node = longest path length from node to leaf path �������� node ���� leaf path length = B D Whose height = 1 ? B, F เครอตราช ACE length = 2 Tree Height= 3 = Root's Height of C = ? = 2 C E F G Leaf Height = 0 รศ. ดร. บญธร Height of A = ? = 3 ACFG length = 3 ABD length = 2 ����� branch �� path Empty Tree Height = ? r A = -1 รศ. กฤตวน ศรบรณ Height: ��� leaf ����� node KMITL 01076249 Data Structures & Algorithms : Tre 3
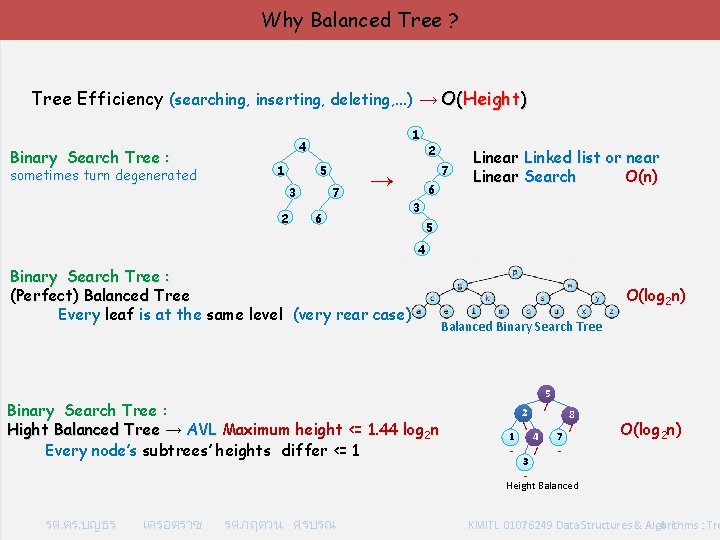
Why Balanced Tree ? Tree Efficiency (searching, inserting, deleting, . . . ) → O(Height) Binary Search Tree : sometimes turn degenerated 1 4 1 5 3 2 7 7 → 6 2 6 Linear Linked list or near Linear Search O(n) 3 5 4 Binary Search Tree : (Perfect) Balanced Tree Every leaf is at the same level (very rear case) Binary Search Tree : Hight Balanced Tree → AVL Maximum height <= 1. 44 log 2 n Every node’s subtrees’ heights differ <= 1 O(log 2 n) Balanced Binary Search Tree 5 / 2 1 - 3 4 / 8 7 / - O(log 2 n) - Height Balanced รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Tre 4
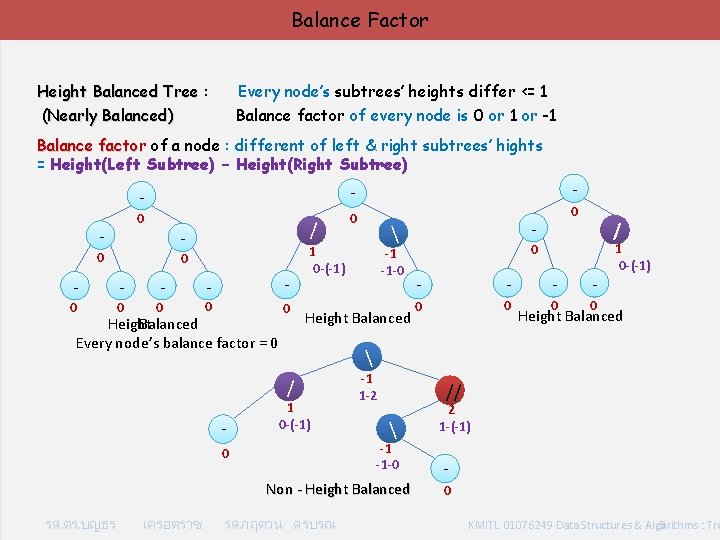
Balance Factor Height Balanced Tree : (Nearly Balanced) Every node’s subtrees’ heights differ <= 1 Balance factor of every node is 0 or 1 or -1 Balance factor of a node : different of left & right subtrees’ hights = Height(Left Subtree) – Height(Right Subtree) - - - 0 0 / - 0 0 - - - 0 0 0 - - 0 Height Balanced Every node’s balance factor = 0 0 -1 -1 -0 Height Balanced 1 0 -(-1) -1 1 -2 0 - - 0 0 1 0 -(-1) Height Balanced // -1 -1 -0 Non - Height Balanced เครอตราช / 0 รศ. ดร. บญธร 0 - 1 0 -(-1) / - - รศ. กฤตวน ศรบรณ 2 1 -(-1) 0 KMITL 01076249 Data Structures & Algorithms : Tre 5
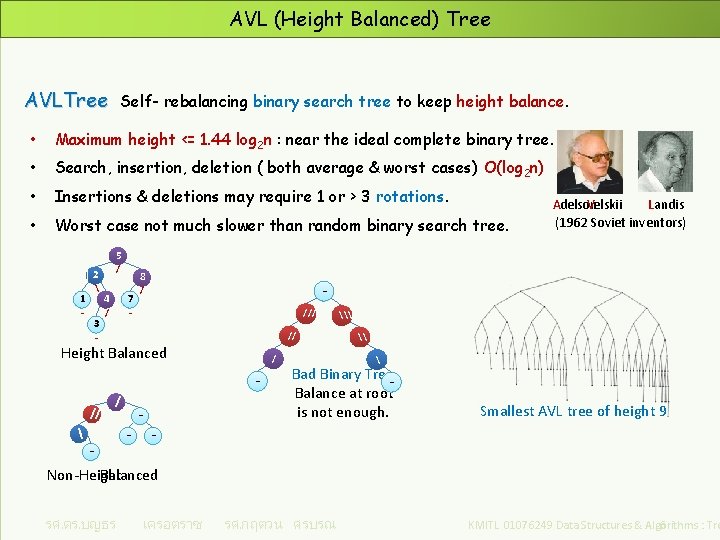
AVL (Height Balanced) Tree AVLTree Self- rebalancing binary search tree to keep height balance. • Maximum height <= 1. 44 log 2 n : near the ideal complete binary tree. • Search, insertion, deletion ( both average & worst cases) O(log 2 n) • Insertions & deletions may require 1 or > 3 rotations. • Worst case not much slower than random binary search tree. Adelson. Velskii Landis (1962 Soviet inventors) 5 / 2 1 - 3 8 7 4 - / /// // - Height Balanced / // / - - - \ \ Bad Binary Tree Balance at root is not enough. Smallest AVL tree of height 9 Non-Height Balanced รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Tre 6

Searching in AVL = Searching in BST AVL is a binary search tree. Review Searching a BST (Binary Search Tree). • Compare search key against key in node start from root. • Follow associated link (recursively). − Left link if search key < key in node − Right link if search key ≥ key in node Ex. Search for 3 3<5 5 3≥ 2 2 1 found 3 รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ 4 3 7 8 9 3<4 KMITL 01076249 Data Structures & Algorithms : Tre 7
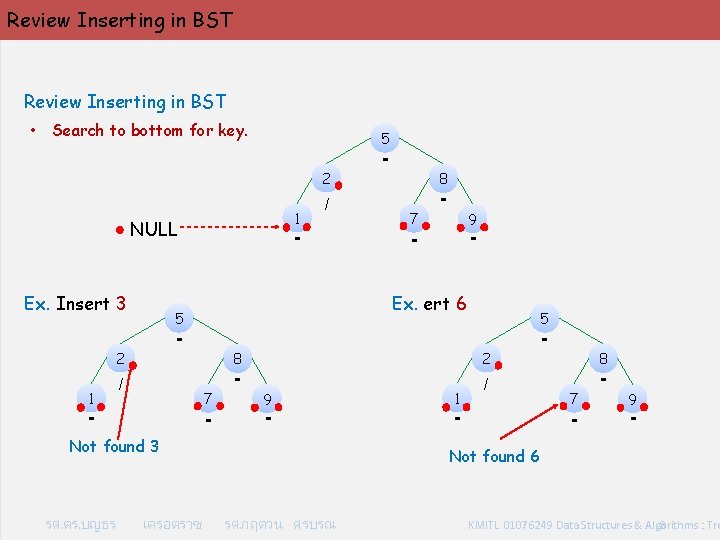
Review Inserting in BST • Search to bottom for key. 5 2 1 NULL Ex. Insert 3 - - 7 9 - - / 7 - 9 - Not found 3 เครอตราช 5 2 8 - รศ. ดร. บญธร 8 Ex. ert 6 5 2 1 / - - 8 - 7 - 9 - Not found 6 รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Tre 8
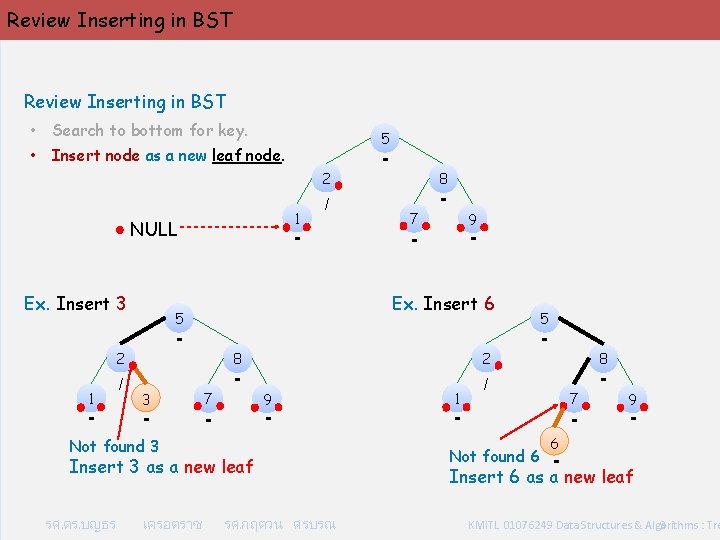
Review Inserting in BST • Search to bottom for key. • Insert node as a new leaf node. 5 2 1 NULL Ex. Insert 3 1 - - - 7 9 - - - 2 8 - 3 - 7 9 - - Insert 3 as a new leaf เครอตราช 1 5 - 8 - / 7 - - 9 - 6 Not found 3 รศ. ดร. บญธร 8 Ex. Insert 6 5 2 / / - รศ. กฤตวน ศรบรณ Not found 6 - Insert 6 as a new leaf KMITL 01076249 Data Structures & Algorithms : Tre 9
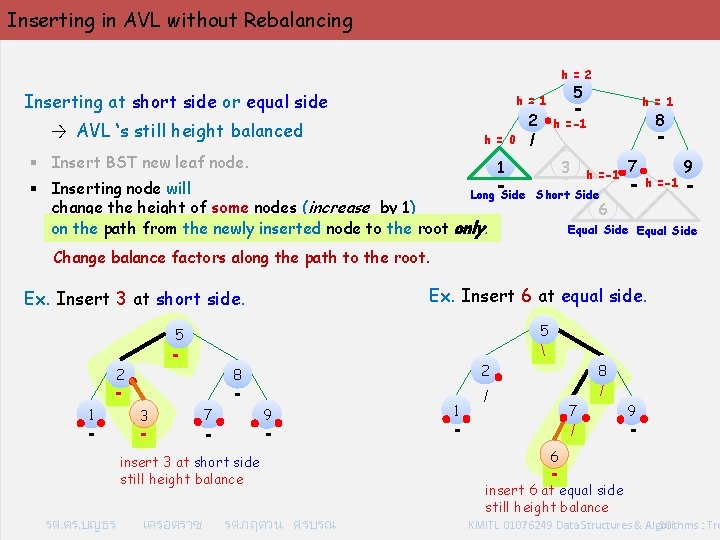
Inserting in AVL without Rebalancing h = 2 Inserting at short side or equal side 5 h = 1 2 → AVL ‘s still height balanced h = 0 § Insert BST new leaf node. 8 h =-1 / 1 § Inserting node will Long Side change the height of some nodes (increase by 1) on the path from the newly inserted node to the root only. h = 1 - 3 - h =-1 Short Side 7 - h =-1 9 - 6 Equal Side Change balance factors along the path to the root. Ex. Insert 6 at equal side. Ex. Insert 3 at short side. 5 5 - 2 1 - 2 8 - 3 - 7 9 - - insert 3 at short side still height balance รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ 1 8 / / 7 - / 9 - 6 - insert 6 at equal side still height balance KMITL 01076249 Data Structures & Algorithms : Tre 10
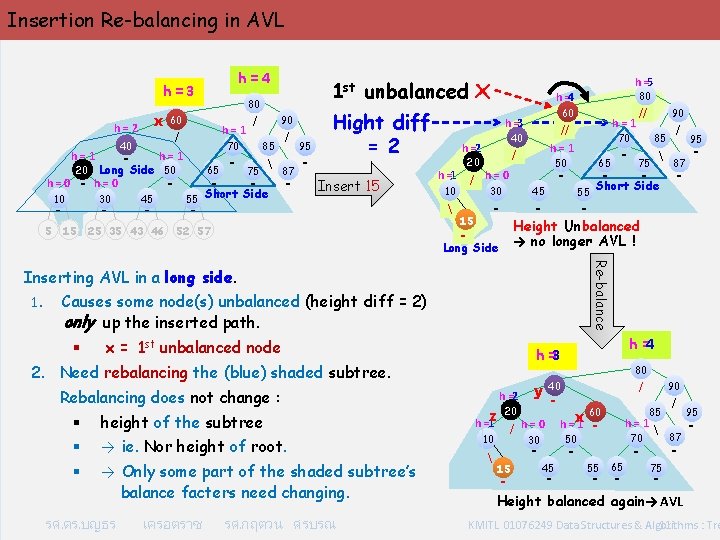
Insertion Re-balancing in AVL x h=2 40 - h=1 10 30 - 5 - 15 80 60 h=1 / h=1 45 - 25 35 43 46 / 70 Long Side 50 h=0 - h=0 20 65 - 55 - 1 st unbalanced x h=4 h=3 - 90 85 75 - Short Side / 87 - 95 - Hight diff = 2 Insert 15 52 57 60 / h=0 30 - 15 50 - 55 - x = 1 st unbalanced node height of the subtree → ie. Nor height of root. § → Only some part of the shaded subtree’s balance facters need changing. รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ - 87 - - Short Side h =4 h =3 2. Need rebalancing the (blue) shaded subtree. § § 75 95 Re-balance Inserting AVL in a long side. 1. Causes some node(s) unbalanced (height diff = 2) only up the inserted path. Rebalancing does not change : / 85 Height Unbalanced → no longer AVL ! Long Side § - 65 - 45 90 70 h=1 / 20 // h=1 // 40 h =2 10 80 h =4 h =3 h =1 h =5 h =2 z h =1 10 20 / y / 40 - h=0 x h=1 30 50 - 15 80 45 - 60 - h=1 70 90 85 55 - 65 - 87 95 - - / 75 Height balanced again→ AVL KMITL 01076249 Data Structures & Algorithms : Tre 11
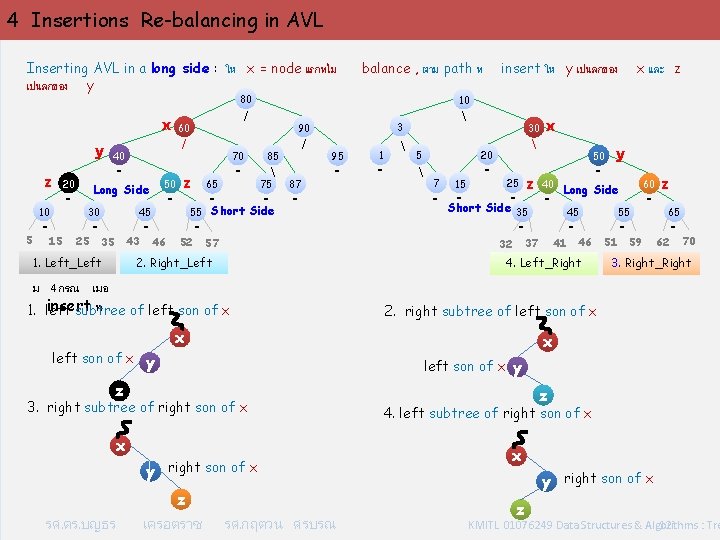
4 Insertions Re-balancing in AVL Inserting AVL in a long side : ให x = node แรกทไม เปนลกของ y balance , ตาม path ท 80 x y z 20 - 10 5 - 15 50 Long Side 25 - 45 30 - / 40 - 43 35 1. Left_Left - 46 / 60 70 z 65 55 52 - - - / 75 - Short Side 87 3 95 - - 57 1 - 5 30 20 7 - 15 - - z 25 - Short Side 35 32 2. Right_Left - 50 40 - 37 - y 60 Long Side 45 41 - 46 55 51 - - 59 z 65 62 - 70 3. Right_Right 2. right subtree of left son of x x x left son of x y z 3. right subtree of right son of x x y right son of x z รศ. ดร. บญธร x 4. Left_Right ม 4 กรณ เมอ insert ท 1. left subtree of left son of x x และ z 10 90 85 insert ให y เปนลกของ เครอตราช รศ. กฤตวน ศรบรณ z 4. left subtree of right son of x x y right son of x z KMITL 01076249 Data Structures & Algorithms : Tre 12
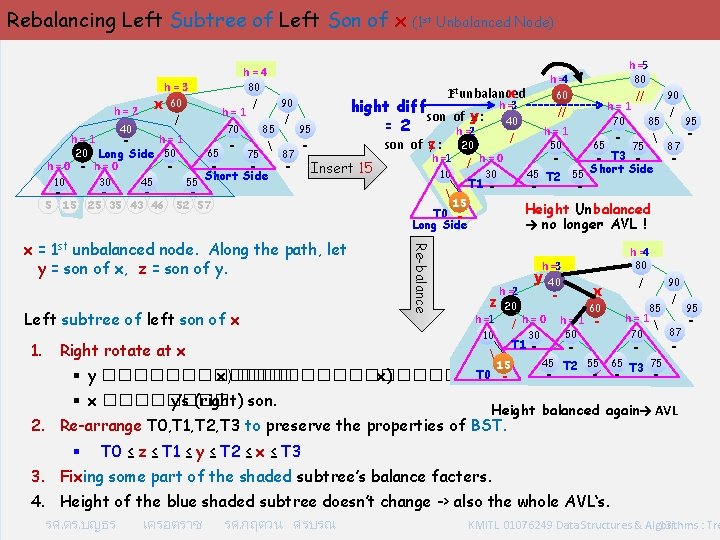
Rebalancing Left Subtree of Left Son of x (1 st Unbalanced Node) h=4 x h=2 40 - h=1 80 h=3 60 h=1 / 70 h=1 20 Long Side 50 h=0 - h=0 10 5 - 30 15 - 45 - 25 35 43 46 / 65 - - 55 - 85 75 - 1 st unbalanced x 90 Short Side / 95 87 - - 52 57 h =1 Re-balance Right rotate at x 65 - 90 85 75 - T 3 - - / 87 95 - - Short Side 45 T 2 55 T 1 - - Height Unbalanced → no longer AVL ! h =4 80 h =3 z h =1 h =2 20 / 10 y 40 15 / x - 60 h=1 - h=0 h=1 70 50 30 T 1 - T 0 ������ x) �������� x) § x ���� y’s (right) son. 50 - 30 15 // 70 h=1 / / h=0 10 h=1 // 40 20 80 60 h =3 T 0 Long Side Left subtree of left son of x § y son of y : z Insert 15 x = 1 st unbalanced node. Along the path, let y = son of x, z = son of y. 1. hight diff son of x : y = 2 h =5 h =4 45 - 90 85 87 95 - - / T 2 55 65 T 3 75 - - - Height balanced again→ AVL 2. Re-arrange T 0, T 1, T 2, T 3 to preserve the properties of BST. § T 0 ≤ z ≤ T 1 ≤ y ≤ T 2 ≤ x ≤ T 3 3. Fixing some part of the shaded subtree’s balance facters. 4. Height of the blue shaded subtree doesn’t change -> also the whole AVL‘s. รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Tre 13
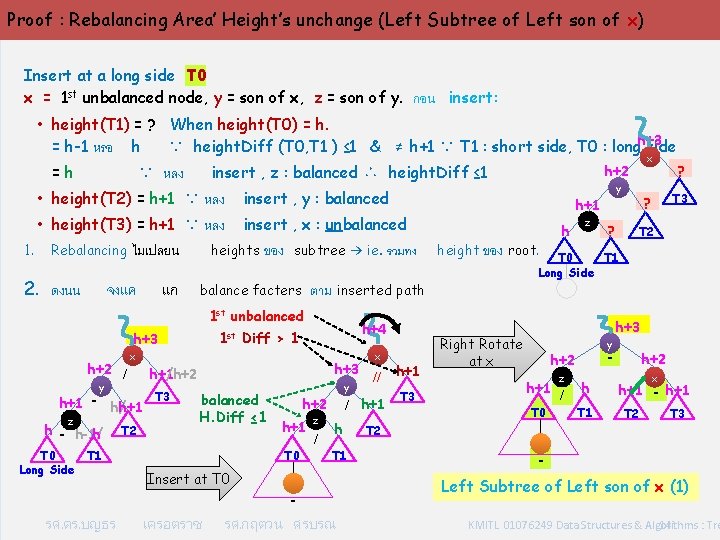
Proof : Rebalancing Area’ Height’s unchange (Left Subtree of Left son of x) Insert at a long side T 0 x = 1 st unbalanced node, y = son of x, z = son of y. กอน insert: • height(T 1) = ? When height(T 0) = h-1 หรอ h ∵ height. Diff (T 0, T 1 ) ≤ 1 & ≠ h+1 ∵ T 1 : short side, T 0 : longh+3 side x h+2 ? =h ∵ หลง insert , z : balanced ∴ height. Diff ≤ 1 • height(T 2) = h+1 ∵ หลง • height(T 3) = h+1 ∵ หลง 1. Rebalancing 2. ดงนน ไมเปลยน จงแค แก insert , y : balanced ของ subtree → ie. รวมทง balance facters ตาม h+2 / y h - h-1/ h T 0 T 1 Long Side T 2 h+3 h+1 /h+2 h+1 - h/h+1 z h+4 1 st Diff > 1 x T 3 balanced H. Diff ≤ 1 y / T 1 Insert at T 0 - รศ. ดร. บญธร เครอตราช x // h+1 h+2 / h+1 z h T 2 T 0 height ของ root. inserted path 1 st unbalanced h+3 h+1 insert , x : unbalanced heights รศ. กฤตวน ศรบรณ T 3 y h z ? T 3 ? T 2 T 0 T 1 Long Side h+3 Right Rotate at x y - h+2 z h+1 / T 0 h T 1 h+2 x h+1 - h+1 T 2 T 3 - Left Subtree of Left son of x (1) KMITL 01076249 Data Structures & Algorithms : Tre 14
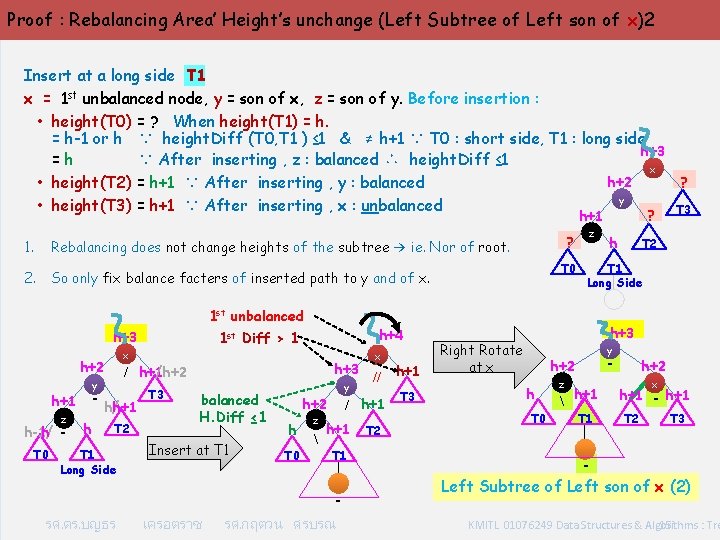
Proof : Rebalancing Area’ Height’s unchange (Left Subtree of Left son of x)2 Insert at a long side T 1 x = 1 st unbalanced node, y = son of x, z = son of y. Before insertion : • height(T 0) = ? When height(T 1) = h-1 or h ∵ height. Diff (T 0, T 1 ) ≤ 1 & ≠ h+1 ∵ T 0 : short side, T 1 : long side h+3 =h ∵ After inserting , z : balanced ∴ height. Diff ≤ 1 x h+2 ? • height(T 2) = h+1 ∵ After inserting , y : balanced y • height(T 3) = h+1 ∵ After inserting , x : unbalanced ? T 3 h+1 1. Rebalancing does not change heights of the subtree → ie. Nor of root. 2. So only fix balance facters of inserted path to y and of x. 1 st unbalanced h+3 x h+2 - z h-1/ h T 0 h h+3 /h+2 / h+1 y h+1 h+4 1 st Diff > 1 h/h+1 T 2 T 1 Long Side T 3 balanced H. Diff ≤ 1 Insert at T 1 y h+2 h T 0 z เครอตราช // h+1 h+1 T 1 รศ. ดร. บญธร x รศ. กฤตวน ศรบรณ T 2 T 3 z ? T 0 h T 2 T 1 Long Side h+3 Right Rotate at x y - h+2 h T 0 z h+1 T 1 h+2 x h+1 - h+1 T 2 T 3 - Left Subtree of Left son of x (2) KMITL 01076249 Data Structures & Algorithms : Tre 15
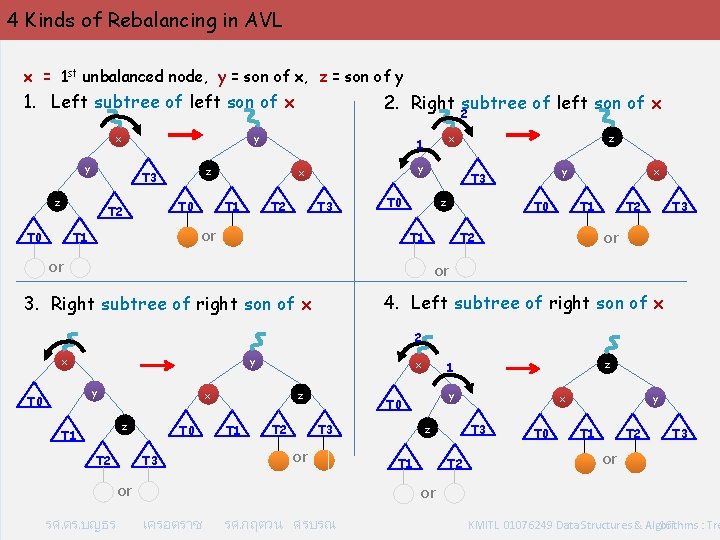
4 Kinds of Rebalancing in AVL x = 1 st unbalanced node, y = son of x, z = son of y 1. Left subtree of left son of x x T 0 y x T 1 T 2 T 3 y T 3 T 0 or T 1 z x 1 z T 3 T 2 T 0 2 y y z 2. Right subtree of left son of x z T 0 T 1 or x T 1 T 2 T 3 or T 2 or 4. Left subtree of right son of x 3. Right subtree of right son of x 2 y x y T 0 z x z T 1 x T 2 T 0 T 3 T 1 T 2 or or รศ. ดร. บญธร y T 0 T 3 z 1 T 3 z T 1 T 2 y x T 0 T 2 T 1 T 3 or or เครอตราช รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Tre 16
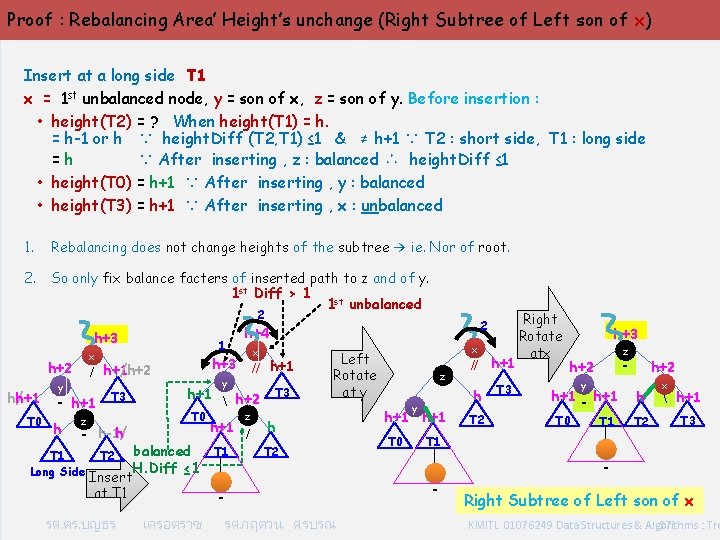
Proof : Rebalancing Area’ Height’s unchange (Right Subtree of Left son of x) Insert at a long side T 1 x = 1 st unbalanced node, y = son of x, z = son of y. Before insertion : • height(T 2) = ? When height(T 1) = h-1 or h ∵ height. Diff (T 2, T 1) ≤ 1 & ≠ h+1 ∵ T 2 : short side, T 1 : long side =h ∵ After inserting , z : balanced ∴ height. Diff ≤ 1 • height(T 0) = h+1 ∵ After inserting , y : balanced • height(T 3) = h+1 ∵ After inserting , x : unbalanced 1. Rebalancing does not change heights of the subtree → ie. Nor of root. 2. So only fix balance facters of inserted path to z and of y. 1 st Diff > 1 1 st unbalanced 2 h+3 x h+2 h/h+1 T 0 - h+1 T 3 z h - h-1/ T 1 T 2 Long Side Insert y h+1 h+2 T 0 z h+1 / T 1 balanced H. Diff ≤ 1 at T 1 รศ. ดร. บญธร x h+3 // h+1 /h+2 / h+1 y h 1 2 h+4 T 3 h T 2 เครอตราช x Left Rotate at y รศ. กฤตวน ศรบรณ z h y h+1 T 0 // h+1 T 2 T 3 Right Rotate atx h+3 z - h+2 y h+1 - h+1 T 0 T 1 h+2 h T 2 x h+1 T 3 T 1 - Right Subtree of Left son of x KMITL 01076249 Data Structures & Algorithms : Tre 17
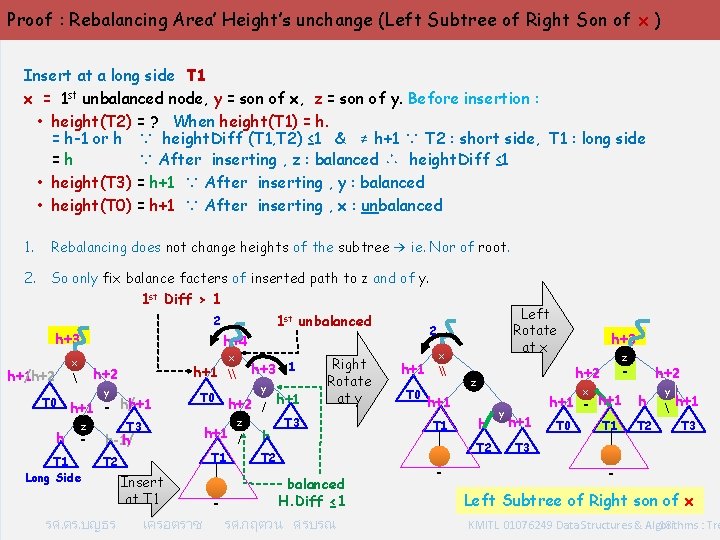
Proof : Rebalancing Area’ Height’s unchange (Left Subtree of Right Son of x ) Insert at a long side T 1 x = 1 st unbalanced node, y = son of x, z = son of y. Before insertion : • height(T 2) = ? When height(T 1) = h-1 or h ∵ height. Diff (T 1, T 2) ≤ 1 & ≠ h+1 ∵ T 2 : short side, T 1 : long side =h ∵ After inserting , z : balanced ∴ height. Diff ≤ 1 • height(T 3) = h+1 ∵ After inserting , y : balanced • height(T 0) = h+1 ∵ After inserting , x : unbalanced 1. Rebalancing does not change heights of the subtree → ie. Nor of root. 2. So only fix balance facters of inserted path to z and of y. 1 st Diff > 1 1 st unbalanced 2 h+3 h+1 /h+2 h x h+1 \ h+3 h+2 T 0 2 h+4 x y h+1 - h/h+1 z - T 1 Long Side h-1/ h h+2 / h+1 z h+1 / T 1 T 2 รศ. ดร. บญธร y T 0 T 3 Insert at T 1 เครอตราช - 1 h Right Rotate at y T 3 Left Rotate at x x h+1 \ T 0 balanced H. Diff ≤ 1 รศ. กฤตวน ศรบรณ - - h+2 x h T 2 z h+2 z h+1 T 1 h+3 y h+1 - h+1 h T 0 T 1 T 2 y h+1 T 3 - Left Subtree of Right son of x KMITL 01076249 Data Structures & Algorithms : Tre 18
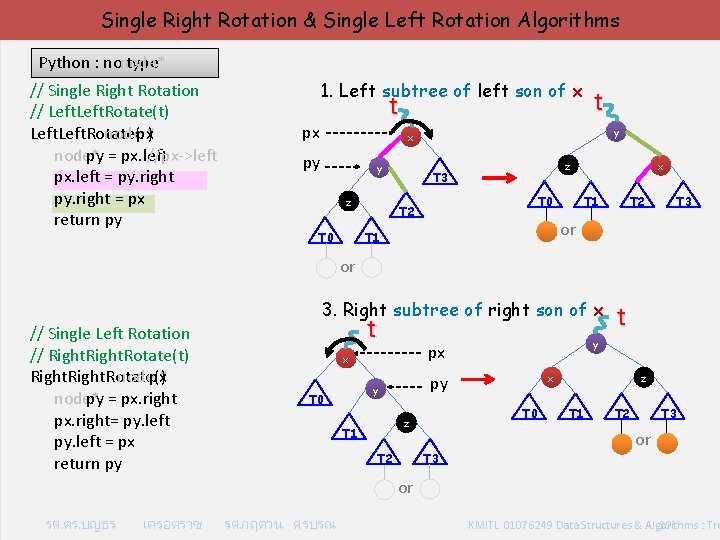
Single Right Rotation & Single Left Rotation Algorithms Python : no type node* // Single Right Rotation // Left. Rotate(t) Left. Rotate( node * px) node* py = px. left //px->left px. left = py. right = px return py 1. Left subtree of left son of x t t px y x py y z T 0 z T 3 T 0 T 2 x T 1 T 2 T 3 or T 1 or 3. Right subtree of right son of x // Single Left Rotation // Right. Rotate(t) Right. Rotate( node * px) node* py = px. right= py. left = px return py t T 0 z T 1 T 2 T 3 z x py y T 0 y px x t T 1 T 2 T 3 or or รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Tre 19
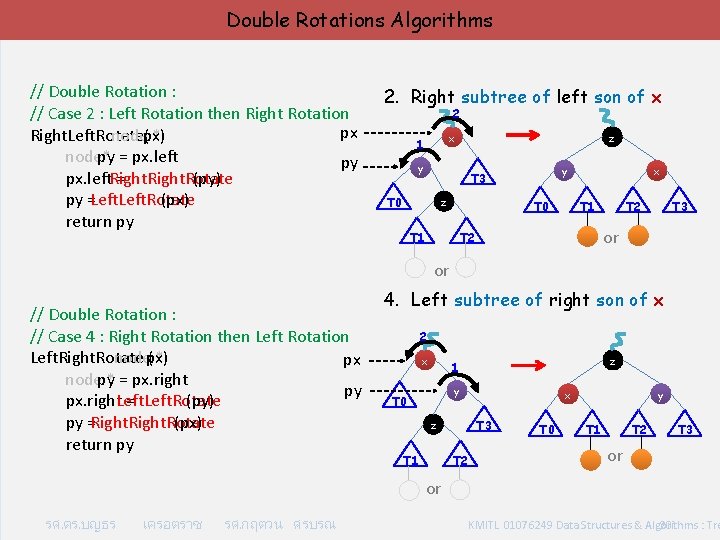
Double Rotations Algorithms // Double Rotation : // Case 2 : Left Rotation then Right Rotation px Right. Left. Rotate( node * px) node* py = px. left py px. left = Right. Rotate (py) py = Left. Rotate (px) return py 2. Right subtree of left son of x 2 z x 1 y y T 3 T 0 z T 0 T 1 x T 1 T 2 T 3 or T 2 or // Double Rotation : // Case 4 : Right Rotation then Left Rotation Left. Right. Rotate ( node * px) px node * py = px. right py px. right = Left. Rotate (py) py = Right. Rotate (px) return py 4. Left subtree of right son of x 2 x z 1 y T 0 T 3 z T 1 y x T 2 T 0 T 2 T 1 T 3 or or รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Tre 20
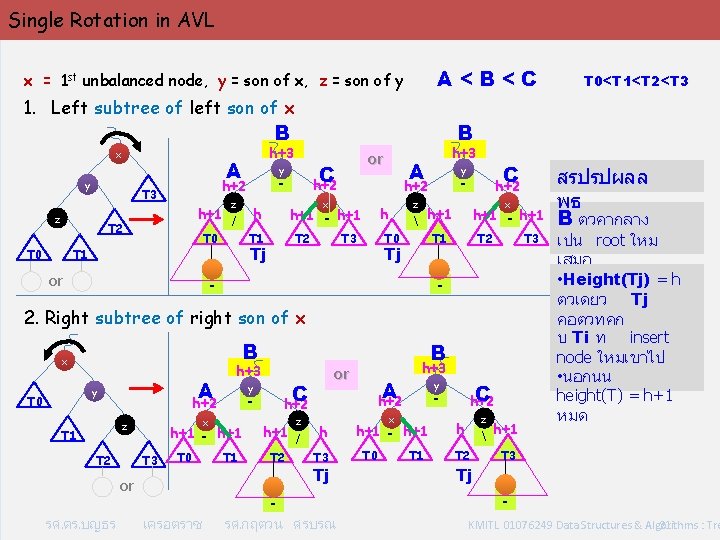
Single Rotation in AVL A<B<C x = 1 st unbalanced node, y = son of x, z = son of y 1. Left subtree of left son of x B x y z z h+1 / T 2 T 0 - T 1 or T 2 Tj A h h+1 - h+1 T 1 h+3 T 0 T 3 - h+2 z x h+1 - h+1 T 1 Tj C y h+2 x h T 0 or C h+2 y h+2 T 3 B h+3 A T 2 T 3 - - 2. Right subtree of right son of x B x A y T 0 T 2 - x h+1 - h+1 T 3 T 0 or รศ. ดร. บญธร y h+2 z T 1 h+3 เครอตราช T 1 or C h+2 z h+1 / T 2 T 0<T 1<T 2<T 3 h T 3 Tj รศ. กฤตวน ศรบรณ B A h+2 h+3 y x h+1 - h+1 T 0 C h+2 - T 1 z h h+1 T 2 สรปรปผลล พธ B ตวคากลาง เปน root ใหม เสมอ • Height(Tj) = h ตวเดยว Tj คอตวทคก บ Ti ท insert node ใหมเขาไป • นอกนน height(T) = h+1 หมด T 3 Tj - KMITL 01076249 Data Structures & Algorithms : Tre 21
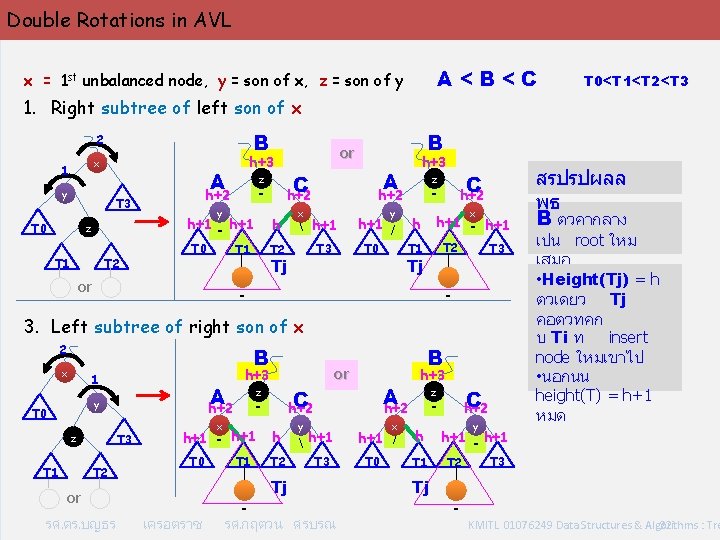
Double Rotations in AVL A<B<C x = 1 st unbalanced node, y = son of x, z = son of y T 0<T 1<T 2<T 3 1. Right subtree of left son of x B 2 x 1 y A z - h+2 T 3 T 0 h+3 y h+1 - h+1 z T 1 T 2 T 0 or h+1 T 0 T 3 Tj - y h+1 / C h+2 z h+2 x T 2 h+3 A C h+2 h T 1 B or x h h+1 - h+1 T 2 T 1 Tj - T 3 - 3. Left subtree of right son of x 2 x B 1 A h+2 y T 0 T 3 z T 1 T 2 x T 2 y h+1 T 3 Tj or รศ. ดร. บญธร - T 1 เครอตราช A h+2 C h+2 z h+1 - h+1 h T 0 B or h+3 รศ. กฤตวน ศรบรณ x h+1 / T 0 h+3 C h+2 z - h T 1 y สรปรปผลล พธ B ตวคากลาง เปน root ใหม เสมอ • Height(Tj) = h ตวเดยว Tj คอตวทคก บ Ti ท insert node ใหมเขาไป • นอกนน height(T) = h+1 หมด h+1 - h+1 T 2 T 3 Tj - KMITL 01076249 Data Structures & Algorithms : Tre 22

Tree 2 3. 4. AVL Tree Height Balanced Tree Which Representions ? 5. n-ary Tree 6. Generic Tree 7. Multiway Search Tree 8. Top Down Tree 9. B-Tree รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ 1. Tree Definitions 2. Binary Tree – Traversals – Binary Search Tree – Representations – Application : Expression Tree KMITL 01076249 Data Structures & Algorithms : Tre 23
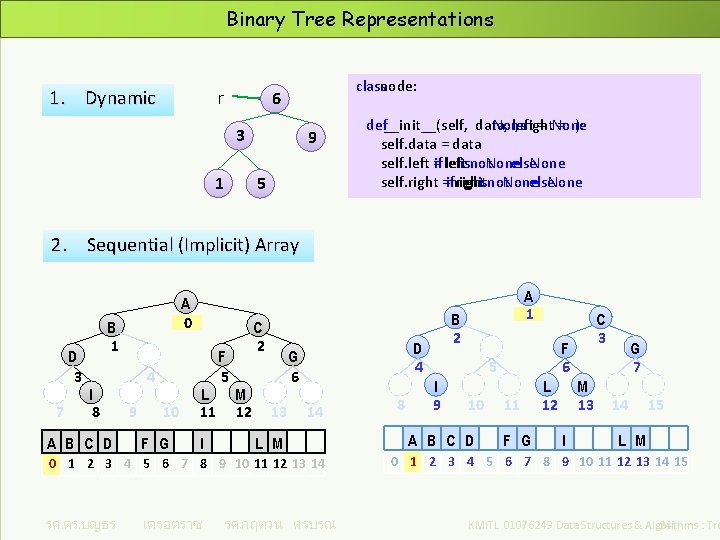
Binary Tree Representations 1. Dynamic r class node: 6 3 1 9 5 def __init__(self, data, left = None , right = None ): self. data = data self. left = left if left is not None else None self. right = right if right is not None else None 2. Sequential (Implicit) Array D 3 7 A 0 B 1 I 8 A B C D 4 9 10 F G L 11 I F 5 C 2 M 12 13 14 L M 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 รศ. ดร. บญธร เครอตราช B 2 D 4 G 6 รศ. กฤตวน ศรบรณ 8 A 1 F 6 5 I 9 10 A B C D C 3 11 F G L 12 M 13 I G 7 14 15 L M 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 KMITL 01076249 Data Structures & Algorithms : Tre 24
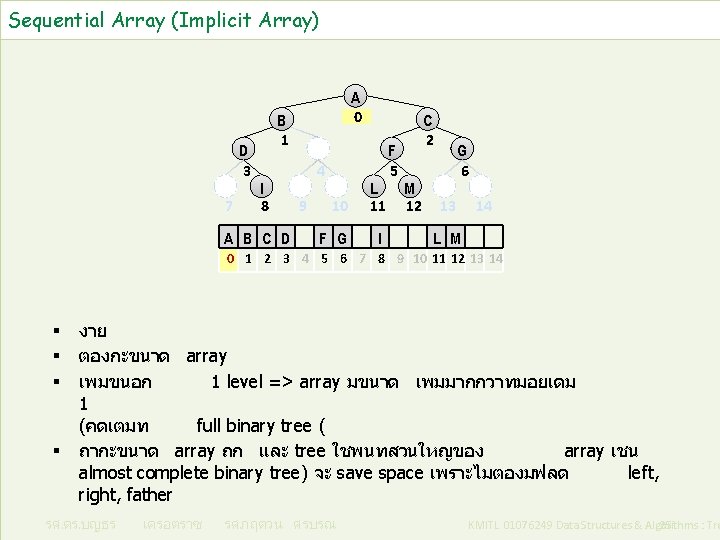
Sequential Array (Implicit Array) D 3 7 A 0 B 1 I 8 A B C D 4 9 10 L 11 F G I F 5 C 2 M 12 G 6 13 14 L M 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 § § งาย ตองกะขนาด array เพมขนอก 1 level => array มขนาด เพมมากกวาทมอยเดม 1 (คดเตมท full binary tree ( ถากะขนาด array ถก และ tree ใชพนทสวนใหญของ array เชน almost complete binary tree) จะ save space เพราะไมตองมฟลด left, right, father รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Tre 25

Tree 2 3. 4. AVL Tree Height Balanced Tree Which Representions ? 5. n-ary Tree 6. Generic Tree 7. Multiway Search Tree 8. Top Down Tree 9. B-Tree รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ 1. Tree Definitions 2. Binary Tree – Traversals – Binary Search Tree – Representations – Application : Expression Tree KMITL 01076249 Data Structures & Algorithms : Tre 27

n-ary (multiway order n) Trees bi-nary Tree ����� node ����� n-ary Tree ����� node ����� Ternary Tree รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ n=3 KMITL 01076249 Data Structures & Algorithms : Linked List 28
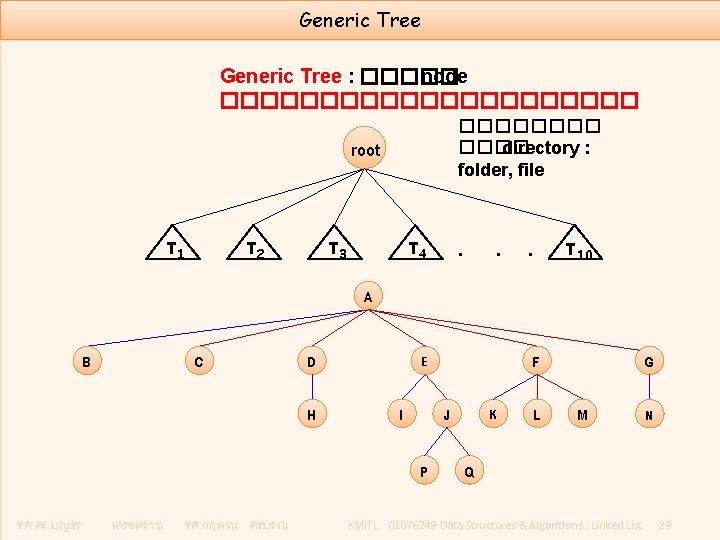
Generic Tree : ����� node ����������� ���� directory : folder, file root T 2 T 1 . T 4 T 3 . . T 10 A C B D H I J P รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ F E K L G M N Q KMITL 01076249 Data Structures & Algorithms : Linked List 29
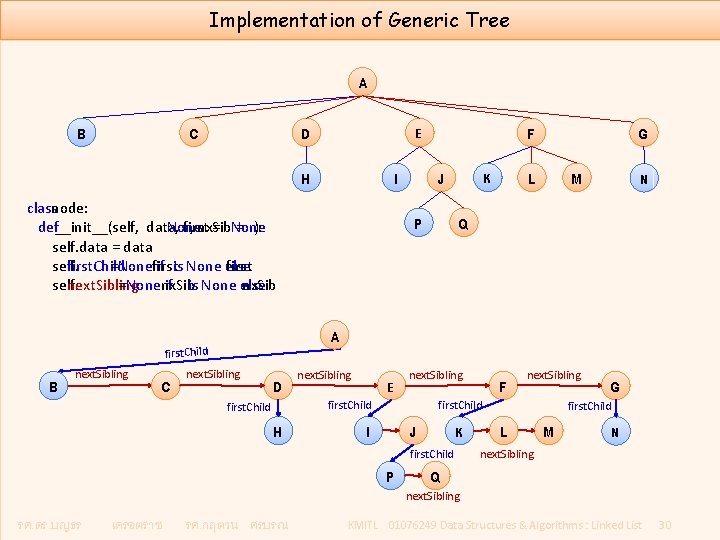
Implementation of Generic Tree A B C D H I class node: def __init__(self, data, first = None , nx. Sib = None ): self. data = data self. first. Child = None if first is None else first self. next. Sibling = None if nx. Sib is None else nx. Sib B C J L K P G M N Q A first. Child next. Sibling F E next. Sibling D next. Sibling E next. Sibling first. Child H F next. Sibling first. Child I J K first. Child P G first. Child L M N next. Sibling Q next. Sibling รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Linked List 30

Tree 2 3. 4. AVL Tree Height Balanced Tree Which Representions ? 5. n-ary Tree 6. Generic Tree 7. Multiway Search Tree v Top Down Tree v Balanced. Tree B-Tree รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ 1. Tree Definitions 2. Binary Tree – Traversals – Binary Search Tree – Representations – Application : Expression Tree KMITL 01076249 Data Structures & Algorithms : Tre 31
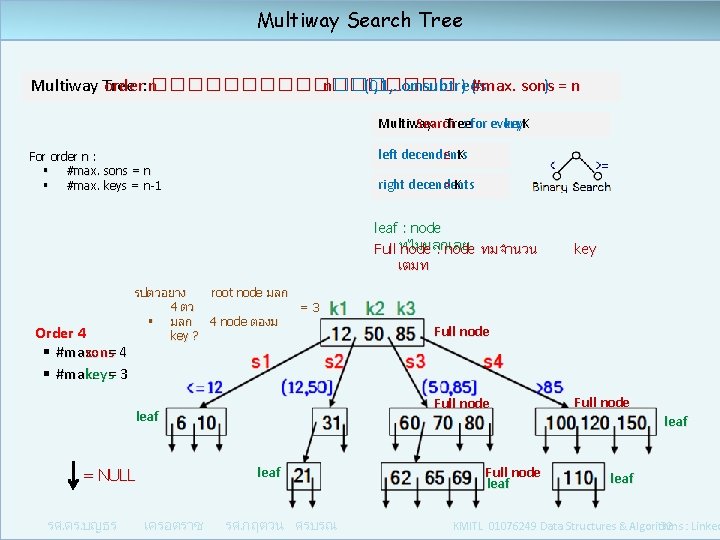
Multiway Search Tree Multiway Tree order n : ��������� n ��� (0, 1, . . . or n subtrees ) (#max. sons = n ) ��������� ��� subtrees Multiway Search Tree : for every key K left decendents ≤ K For order n : § #max. sons = n § #max. keys = n-1 right decendents > K leaf : node Full ทไมมลกเลย node : node ทมจำนวน เตมท Order 4 § #max. sons = 4 § #max. keys = 3 รปตวอยาง root node มลก 4 ตว =3 § มลก 4 node ตองม key ? = NULL รศ. ดร. บญธร Full node leaf เครอตราช Full node leaf key รศ. กฤตวน ศรบรณ Full node leaf KMITL 01076249 Data Structures & Algorithms : Linked 32

Tree 2 3. 4. AVL Tree Height Balanced Tree Which Representions ? 5. n-ary Tree 6. Generic Tree 7. Multiway Search Tree v Top Down Tree v Balanced. Tree B-Tree รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ 1. Tree Definitions 2. Binary Tree – Traversals – Binary Search Tree – Representations – Application : Expression Tree KMITL 01076249 Data Structures & Algorithms : Tre 33

Tree 2 3. 4. AVL Tree Height Balanced Tree Which Representions ? 5. n-ary Tree 6. Generic Tree 7. Multiway Search Tree v Top Down Tree v Balanced. Tree B-Tree รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ 1. Tree Definitions 2. Binary Tree – Traversals – Binary Search Tree – Representations – Application : Expression Tree KMITL 01076249 Data Structures & Algorithms : Tre 35
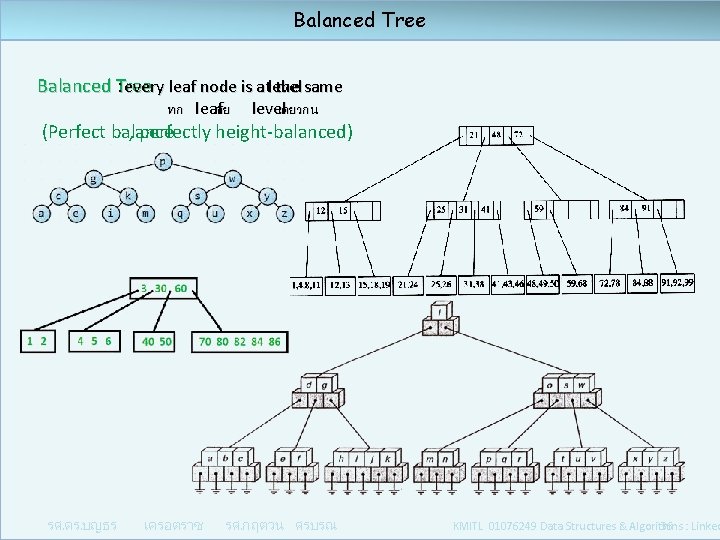
Balanced Tree : every leaf node is at the same level ทก leaf อย level เดยวกน (Perfect balance , perfectly height-balanced) รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Linked 36
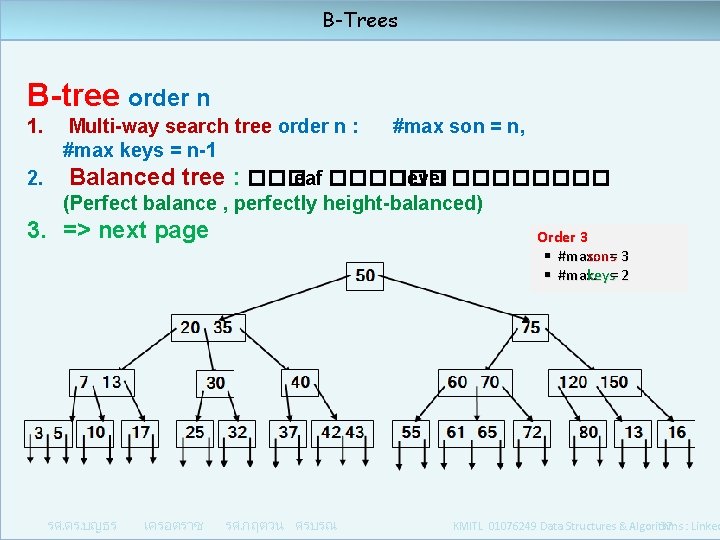
B-Trees B-tree order n 1. Multi-way search tree order n : #max son = n, #max keys = n-1 2. Balanced tree : ��� leaf ������ level ���� (Perfect balance , perfectly height-balanced) 3. => next page รศ. ดร. บญธร เครอตราช Order 3 § #max. sons = 3 § #max. keys = 2 รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Linked 37
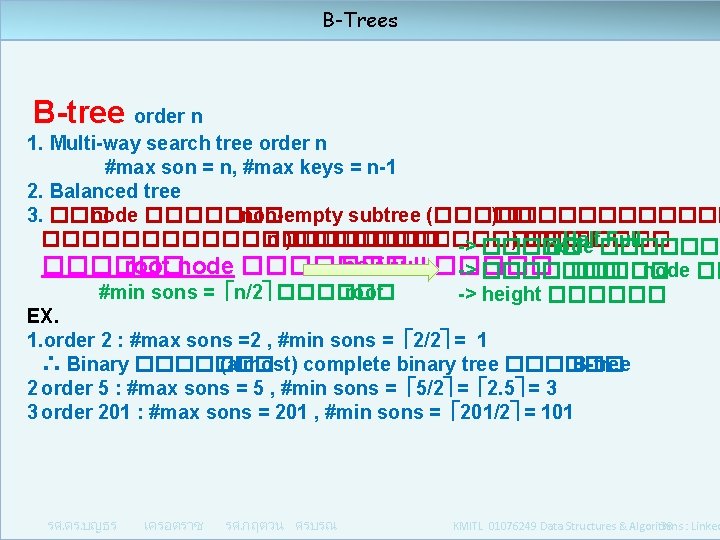
B-Trees B-tree order n 1. Multi-way search tree order n #max son = n, #max keys = n-1 2. Balanced tree 3. ��� node ������� non-empty subtree (����� )������ ���������� n )���������� ) ��� Half Full -> ����� node ������� root node ������� half full ����� -> ������� node �� #min sons = n/2 ������ root -> height ������ EX. 1. order 2 : #max sons =2 , #min sons = 2/2 = 1 ∴ Binary ������� (almost) complete binary tree ������ B-tree 2 order 5 : #max sons = 5 , #min sons = 5/2 = 2. 5 = 3 3 order 201 : #max sons = 201 , #min sons = 201/2 = 101 รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Linked 38

B-Tree Variation order 5 #max son = 5, #max keys = 4 • Half Full #min sons = 5/2 = 2. 5 = 3 )ยกเวน root node) B-tree -> variations • internal nodes : เกบเฉพาะ key เพอประหยด พนท (เกบ data ไดมากกวา • external nodes : เกบ data ทง record คา L กำหนดจำนวน record/node ของ leaf ถา L = 5: #max data = 5, #min data = 5/2 = 2. 5 = 3 รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ เกบทง record ), order กำหนดจำนวนลก KMITL 01076249 Data Structures & Algorithms : Linked 39
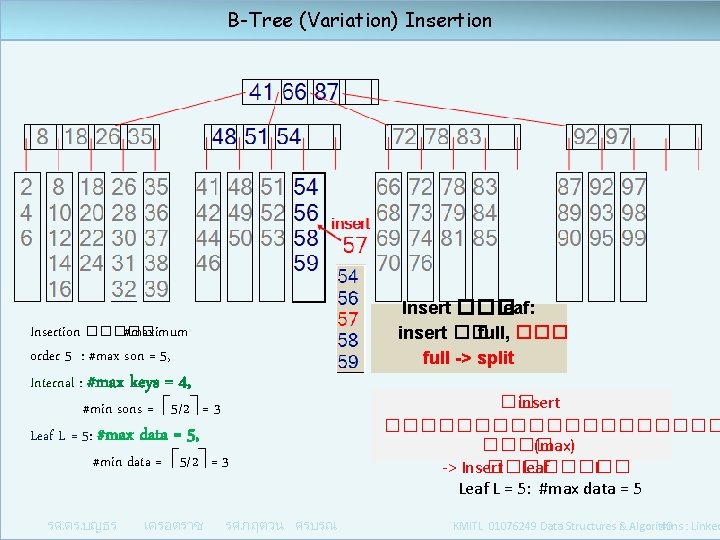
B-Tree (Variation) Insertion ����� #maximum order 5 : #max son = 5, Internal : #max keys = 4, #min sons = 5/2 = 3 Leaf L = 5: #max data = 5, #min data = 5/2 = 3 รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ Insert ��� leaf: insert �� full, ��� full -> split �� insert ���������� (max) -> Insert ��� leaf ����� L Leaf L = 5: #max data = 5 KMITL 01076249 Data Structures & Algorithms : Linked 40
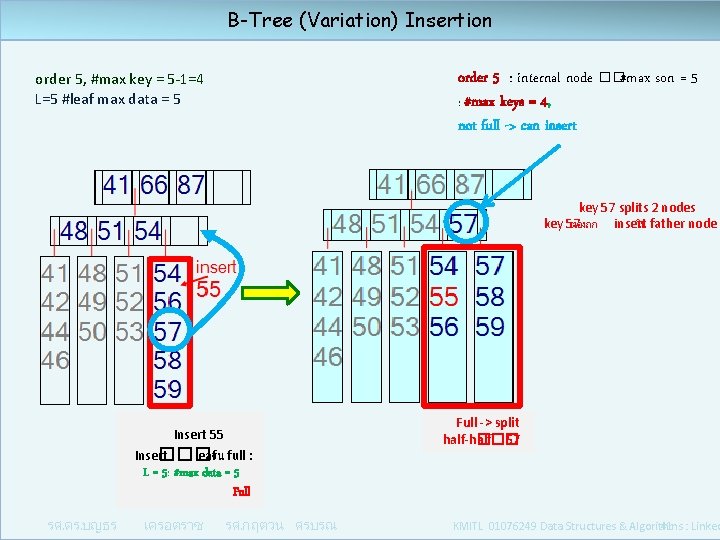
B-Tree (Variation) Insertion order 5 : internal node ��#max son = 5 : #max keys = 4, not full -> can insert order 5, #max key = 5 -1=4 L=5 #leaf max data = 5 key 57 splits 2 nodes key 57 ตองถก insert ใน father node Insert 55 Insert ��� leaf จน full : Full -> split half-half ��� 57 L = 5: #max data = 5 Full รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Linked 41
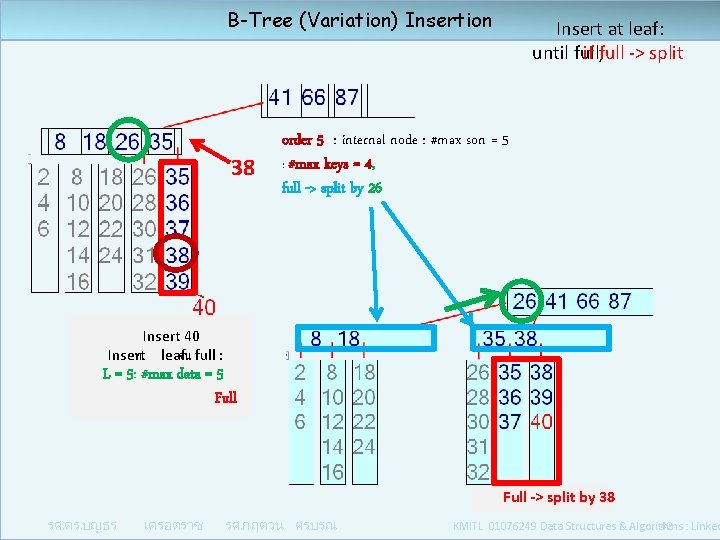
B-Tree (Variation) Insertion 38 Insert at leaf: until full, if full -> split order 5 : internal node : #max son = 5 : #max keys = 4, full -> split by 26 Insert 40 Insert ท leaf จน full : L = 5: #max data = 5 Full -> split by 38 รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Linked 42
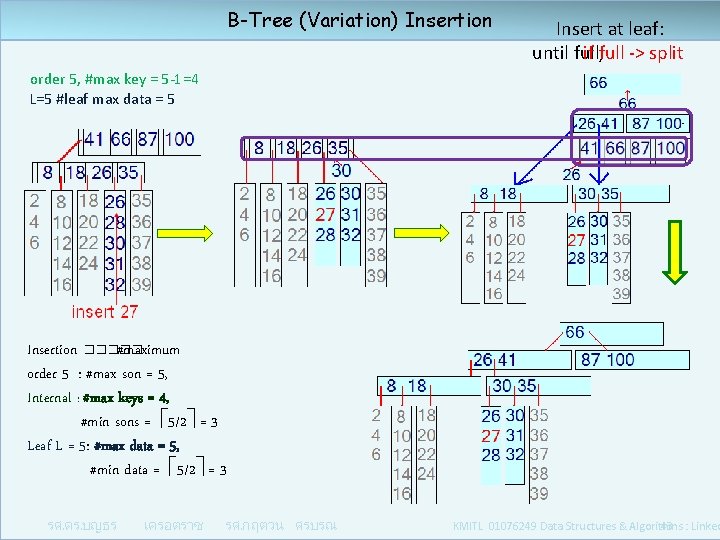
B-Tree (Variation) Insertion Insert at leaf: until full, if full -> split order 5, #max key = 5 -1=4 L=5 #leaf max data = 5 Insertion ����� #maximum order 5 : #max son = 5, Internal : #max keys = 4, #min sons = 5/2 = 3 Leaf L = 5: #max data = 5, #min data = 5/2 = 3 รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Linked 43

B-Tree (Variation) Deletion consider #minimum Internal order 5 : #min sons = 5/2 = 3 #min keys = 2 Leaf L = 5: #max data = 5, #min data = 5/2 = 3 Delete at leaf : insert ระวงไมใหเกน ตองด max delete ระวงไมใหขาด ตองด min until low, if low -> borrow Borrowing 1. ยมพนอง (ผานพอ ) 2. ยมพอ ตอง consolidate พอไมม พอยม -พนองพอ (ผานป ) . . . รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Linked 44

B-Tree (Variation) Deletion Delete at leaf: until low, if low -> borrow Deletion consider #minimum Internal order 5 : #min sons = 5/2 = 3 #min keys = 2 Leaf L = 5: #max data = 5, #min data = 5/2 = 3 Borrowing 1. ยมพนอง (ผานพอ ) เชน del 49 เอา 46 ของพมา รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ 2. ยมพอ ตอง consolidate เชน del 84 พนองไมมใหยม ยมพอ โดยรวม consolidate กบพอ ถาพอ ไมม พอยม -พนองพอ (ผานป ) . . . KMITL 01076249 Data Structures & Algorithms : Linked 45
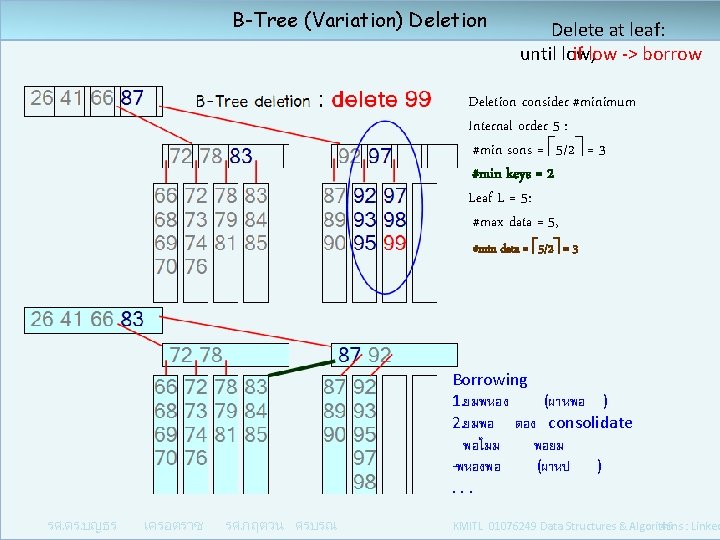
B-Tree (Variation) Deletion Delete at leaf: until low, if low -> borrow Deletion consider #minimum Internal order 5 : #min sons = 5/2 = 3 #min keys = 2 Leaf L = 5: #max data = 5, #min data = 5/2 = 3 Borrowing 1. ยมพนอง (ผานพอ ) 2. ยมพอ ตอง consolidate พอไมม พอยม -พนองพอ (ผานป ) . . . รศ. ดร. บญธร เครอตราช รศ. กฤตวน ศรบรณ KMITL 01076249 Data Structures & Algorithms : Linked 46
- Slides: 46