Tree tree connected graph with no cycle tree


















![Union-Find S[1. . n] for i 1 to n do S[i] i Find-Set(u) return Union-Find S[1. . n] for i 1 to n do S[i] i Find-Set(u) return](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-31.jpg)
![Union-Find S[1. . n] for i 1 to n do S[i] i Find-Set(u) return Union-Find S[1. . n] for i 1 to n do S[i] i Find-Set(u) return](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-32.jpg)

![Union-Find 2 n=|V| S[1. . n] for i 1 to n do S[i] i Union-Find 2 n=|V| S[1. . n] for i 1 to n do S[i] i](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-35.jpg)
![Union-Find 2 n=|V| S[1. . n] for i 1 to n do S[i] i Union-Find 2 n=|V| S[1. . n] for i 1 to n do S[i] i](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-36.jpg)
![Union-Find 2 n=|V| S[1. . n] for i 1 to n do S[i] i Union-Find 2 n=|V| S[1. . n] for i 1 to n do S[i] i](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-37.jpg)
![Union-Find 2 n=|V| S[1. . n] for i 1 to n do S[i] i Union-Find 2 n=|V| S[1. . n] for i 1 to n do S[i] i](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-38.jpg)






![Minimum weight spanning trees for i 1 to n do C[i] C[0]=0 S={} while Minimum weight spanning trees for i 1 to n do C[i] C[0]=0 S={} while](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-53.jpg)
![Minimum weight spanning trees for i 1 to n do C[i] C[0]=0 O(n) S={} Minimum weight spanning trees for i 1 to n do C[i] C[0]=0 O(n) S={}](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-54.jpg)
![Minimum weight spanning trees for i 1 to n do C[i] C[0]=0 O(n) S={} Minimum weight spanning trees for i 1 to n do C[i] C[0]=0 O(n) S={}](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-55.jpg)
![Minimum weight spanning trees for i 1 to n do C[i] C[0]=0 O(log n) Minimum weight spanning trees for i 1 to n do C[i] C[0]=0 O(log n)](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-56.jpg)


- Slides: 58

Tree tree = connected graph with no cycle tree = connected graph with |V|-1 edges tree = graph with |V|-1 edges and no cycles

Tree tree = connected graph with no cycle tree = connected graph with |V|-1 edges tree = graph with |V|-1 edges and no cycles no cycle vertex of degree 1 |V|-1 edges vertex of degree 1 connected no vertex of degree 0 (unless |V|=1)

no cycle vertex of degree 1 Supose not, i. e. , all vertices of degree 2, yet no cycle. Let v 1, . . . , vt be the longest path vt has 2 -neighbors, one different from vt-1. Why cannot take v 1, . . . , vt, u ? Cycle. Contradiction.

|V|-1 edges vertex of degree 1 Suppose all degrees 2. Then |E|=(1/2) deg(v) |V| v V Contradiction. Done.

connected no vertex of degree 0 (unless |V|=1)

Tree connected graph with no cycle connected graph with |V|-1 edges and no cycles no cycle vertex of degree 1 |V|-1 edges vertex of degree 1 connected no vertex of degree 0 (unless |V|=1)

connected graph with no cycle connected graph with |V|-1 edges Induction on |V|. Base case |V|=1. Let G be connected with no cycles. Then G has vertex v of degree 1. Let G’ = G – v. Then G’ is connected and has no cycle. By IH G’ has |V|-2 edges and hence G has |V|-1 edges.

connected graph with no cycle connected graph with |V|-1 edges Induction on |V|. Base case |V|=1. Let G be connected |V|-1 edges. Then G has vertex v of degree 1. Let G’ = G – v. Then G’ is connected and has |V’|-1 edges. By IH G’ has no cycle. Hence G has no cycle.

connected graph with no cycle connected graph with |V|-1 edges and no cycles Assume |V|-1 edges and no cycles. Let |G 1|, . . . , |Gk| be the connected components. Then |E_i| = |V_i| - 1, hence |E| = |V| - k. Thus k = 1.

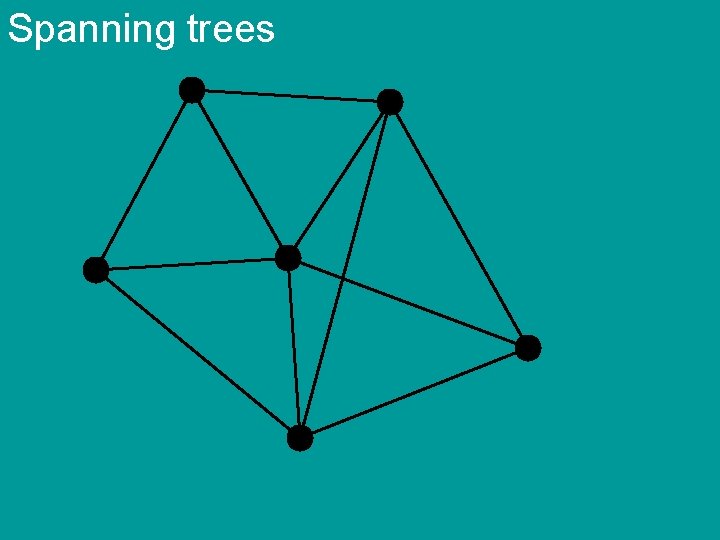
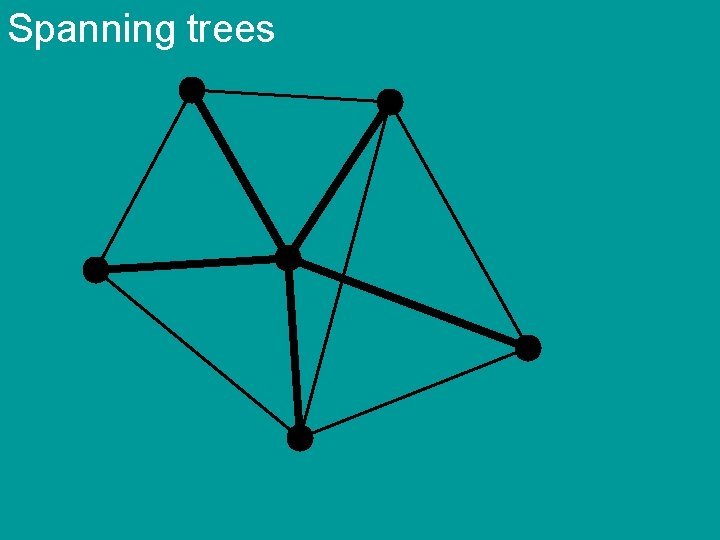
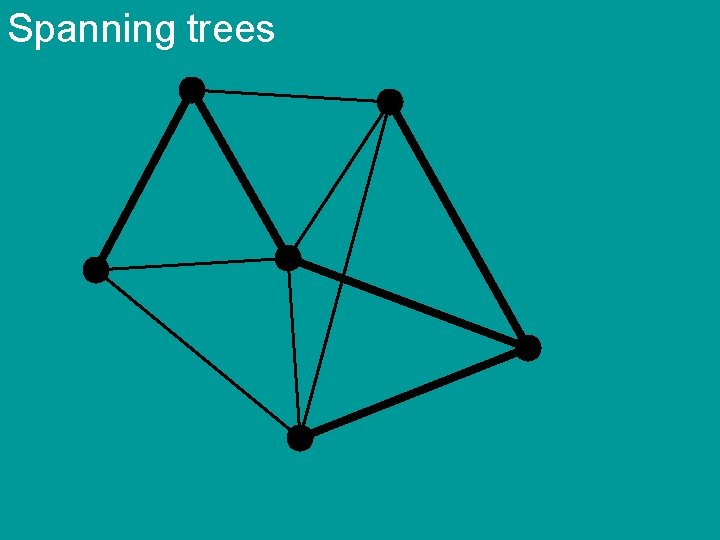
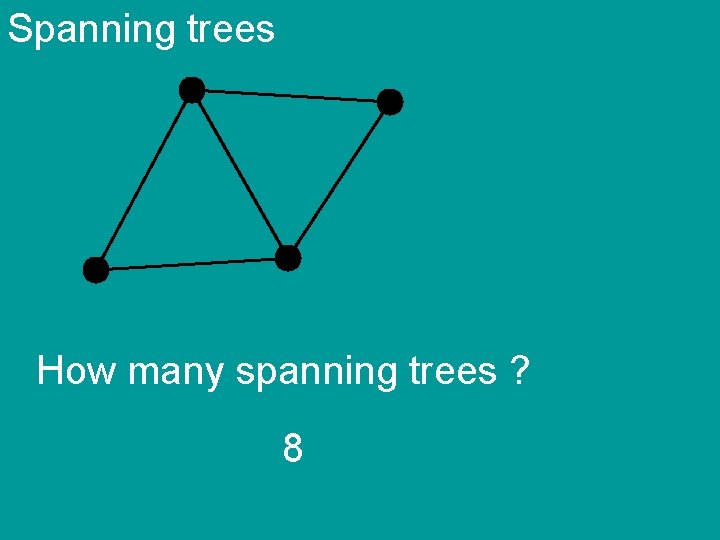
Spanning trees

Spanning trees

Spanning trees

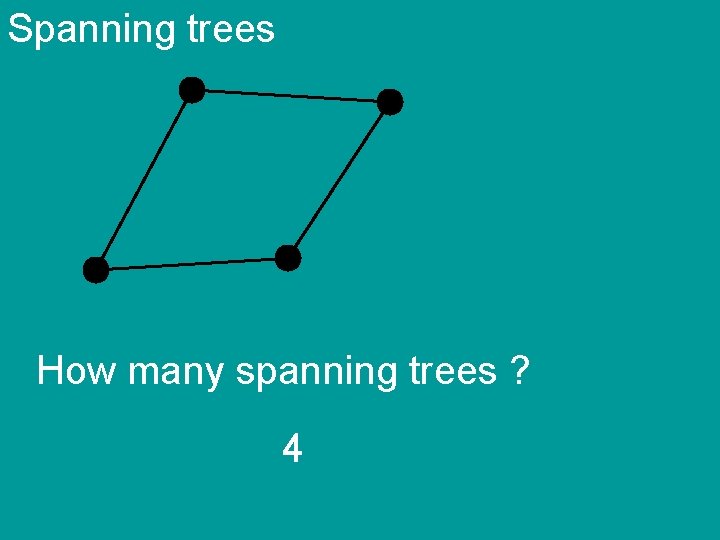
Spanning trees How many spanning trees ?

Spanning trees How many spanning trees ? 4

Spanning trees How many spanning trees ?

Spanning trees How many spanning trees ? 8

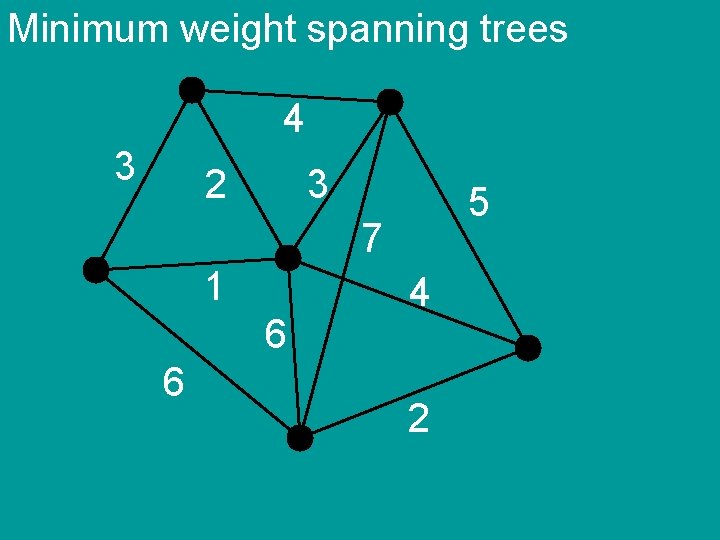
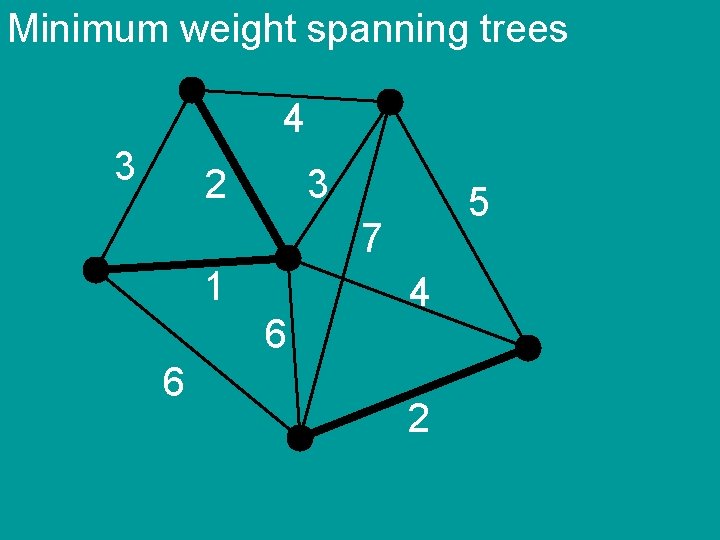
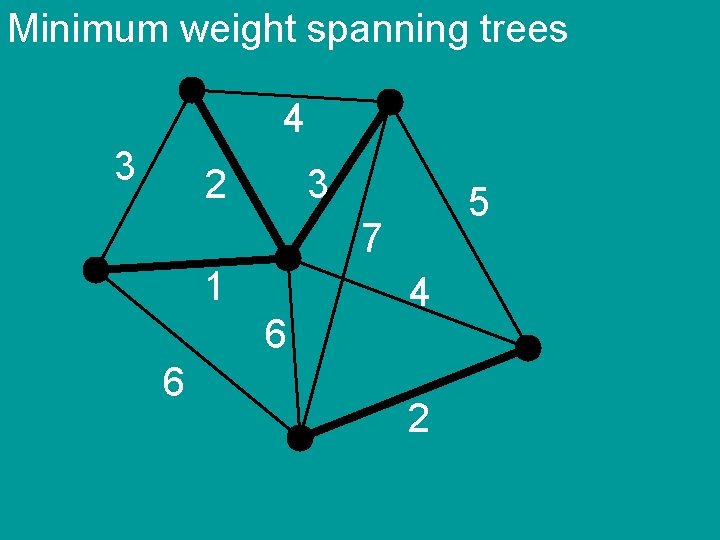
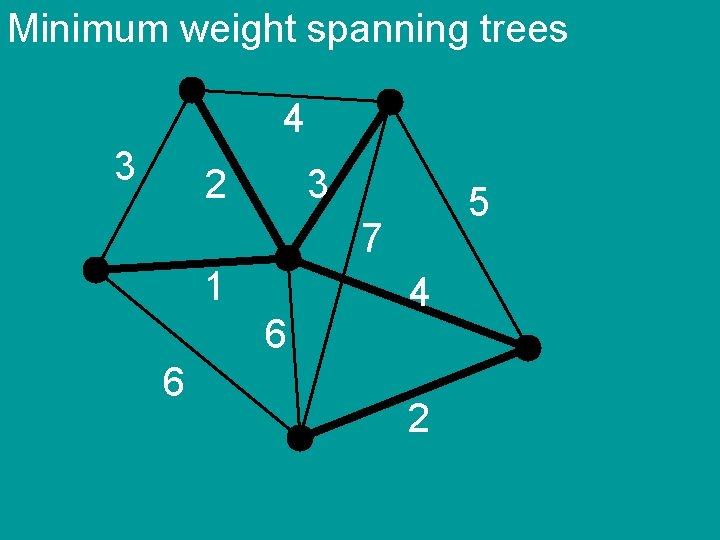
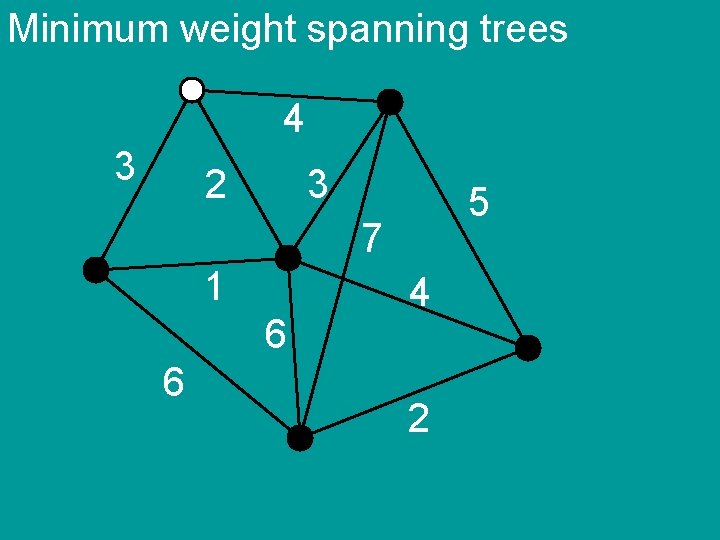
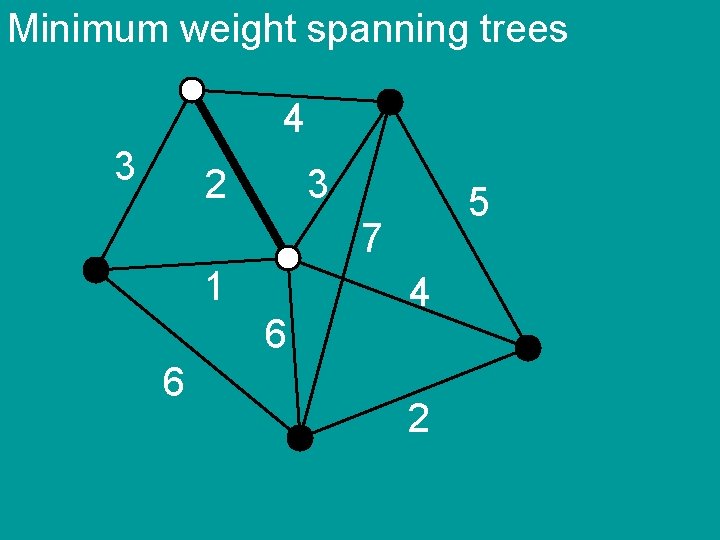
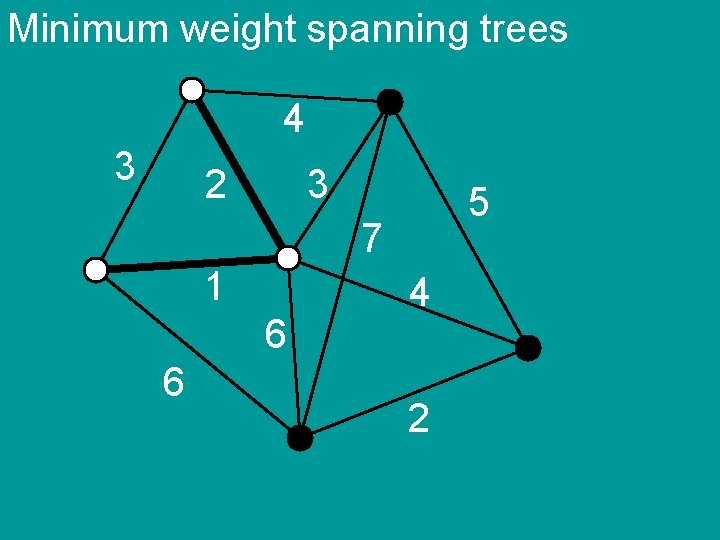
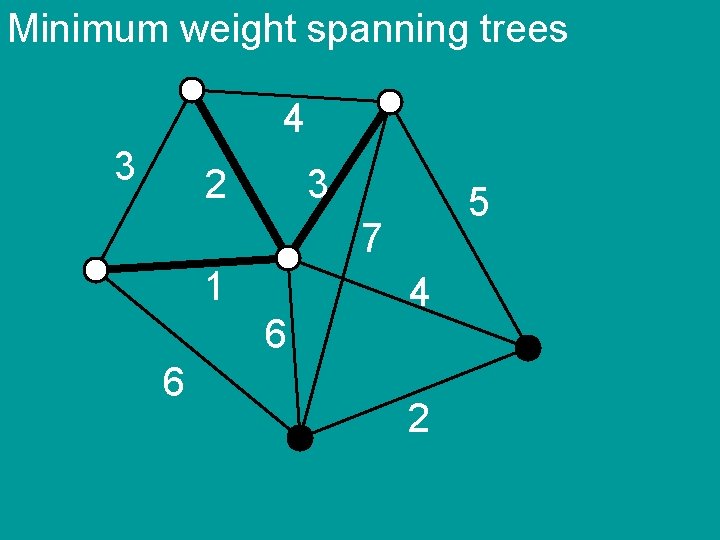
Minimum weight spanning trees 4 3 2 3 5 7 1 6 6 4 2

Minimum weight spanning trees 4 3 2 3 5 7 1 6 6 4 2

Minimum weight spanning trees 4 3 2 3 5 7 1 6 6 4 2

Minimum weight spanning trees 4 3 2 3 5 7 1 6 6 4 2

Minimum weight spanning trees 4 3 2 3 5 7 1 6 6 4 2

Minimum weight spanning trees 4 3 2 3 5 7 1 6 6 4 2

Minimum weight spanning trees Kruskal’s algorithm 1) sort the edges by weight 2) add edges in order if they do not create cycle

Kruskal’s algorithm 1) sort the edges by weight 2) add edges in order if they do not create cycle K = MST output by Kruskal T = optimal MST Is K = T ?

Kruskal’s algorithm 1) sort the edges by weight 2) add edges in order if they do not create cycle K = MST output by Kruskal T = optimal MST Is K = T ? no – e. g. if all edge-weights are the same many optima

Kruskal’s algorithm 1) sort the edges by weight 2) add edges in order if they do not create cycle K = MST output by Kruskal T = optimal MST Assume all edge weights are different. Then K=T. (In particular, unique optimum)

Kruskal’s algorithm 1) sort the edges by weight 2) add edges in order if they do not create cycle K = MST output by Kruskal T = optimal MST G connected, e in a cycle G-e connected

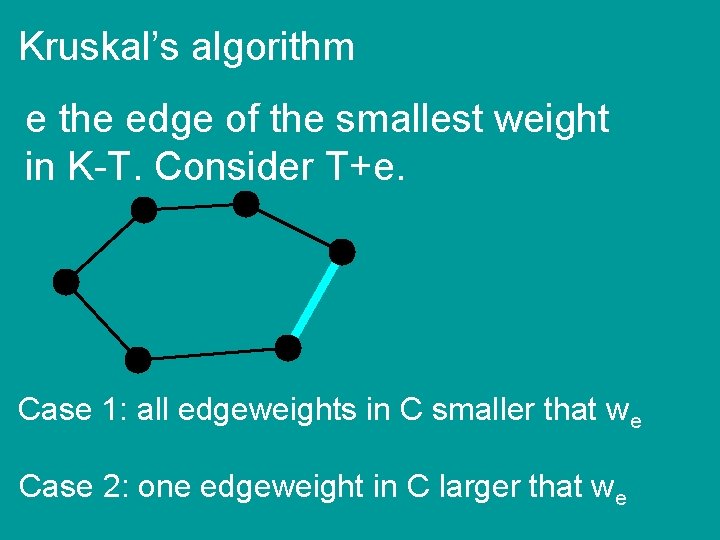
Kruskal’s algorithm K = MST output by Kruskal T = optimal MST G connected, e in a cycle G-e connected e the edge of the smallest weight in K-T. Consider T+e.

Kruskal’s algorithm e the edge of the smallest weight in K-T. Consider T+e. Case 1: all edgeweights in C smaller that we Case 2: one edgeweight in C larger that we

Kruskal’s algorithm 1) sort the edges by weight 2) add edges in order if they do not create cycle Need to maintain components. Find-Set(u) Union(u, v)
![UnionFind S1 n for i 1 to n do Si i FindSetu return Union-Find S[1. . n] for i 1 to n do S[i] i Find-Set(u) return](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-31.jpg)
Union-Find S[1. . n] for i 1 to n do S[i] i Find-Set(u) return S[u] Union(u, v) a S[u] for i 1 to n do if S[i]=a then S[i] S[v]
![UnionFind S1 n for i 1 to n do Si i FindSetu return Union-Find S[1. . n] for i 1 to n do S[i] i Find-Set(u) return](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-32.jpg)
Union-Find S[1. . n] for i 1 to n do S[i] i Find-Set(u) return S[u] O(1) Union(u, v) a S[u] for i 1 to n do if S[i]=a then S[i] S[v] O(n)

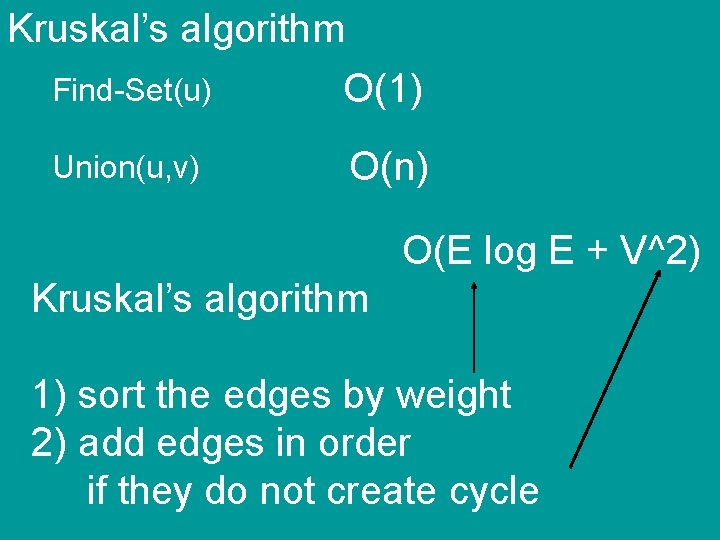
Kruskal’s algorithm Find-Set(u) O(1) Union(u, v) O(n) Kruskal’s algorithm 1) sort the edges by weight 2) add edges in order if they do not create cycle

Kruskal’s algorithm Find-Set(u) O(1) Union(u, v) O(n) O(E log E + V^2) Kruskal’s algorithm 1) sort the edges by weight 2) add edges in order if they do not create cycle
![UnionFind 2 nV S1 n for i 1 to n do Si i Union-Find 2 n=|V| S[1. . n] for i 1 to n do S[i] i](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-35.jpg)
Union-Find 2 n=|V| S[1. . n] for i 1 to n do S[i] i Find-Set(u) while (S[u] u) do u S[u] Union(u, v) S[Find-Set(u)] Find-Set(v) v u
![UnionFind 2 nV S1 n for i 1 to n do Si i Union-Find 2 n=|V| S[1. . n] for i 1 to n do S[i] i](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-36.jpg)
Union-Find 2 n=|V| S[1. . n] for i 1 to n do S[i] i Find-Set(u) while (S[u] u) do u S[u] Union(u, v) S[Find-Set(u)] Find-Set(v) v u
![UnionFind 2 nV S1 n for i 1 to n do Si i Union-Find 2 n=|V| S[1. . n] for i 1 to n do S[i] i](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-37.jpg)
Union-Find 2 n=|V| S[1. . n] for i 1 to n do S[i] i Find-Set(u) while (S[u] u) do u S[u] Union(u, v) S[Find-Set(u)] Find-Set(v) O(n)
![UnionFind 2 nV S1 n for i 1 to n do Si i Union-Find 2 n=|V| S[1. . n] for i 1 to n do S[i] i](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-38.jpg)
Union-Find 2 n=|V| S[1. . n] for i 1 to n do S[i] i Find-Set(u) while (S[u] u) do u S[u] O(log n) Union(u, v) O(log n) u Find-Set(u); v Find-Set(v); if D[u]<D[v] then S[u] v if D[u]>D[v] then S[v] u if D[u]=D[v] then S[u] v; D[v]++

Kruskal’s algorithm Find-Set(u) O(log n) Union(u, v) O(log n) Kruskal’s algorithm 1) sort the edges by weight 2) add edges in order if they do not create cycle

Kruskal’s algorithm Find-Set(u) O(log n) Union(u, v) O(log n) O(E log E + (E+V)log V) Kruskal’s algorithm 1) sort the edges by weight 2) add edges in order if they do not create cycle

Kruskal’s algorithm log E log V 2 = 2 log V = O(log V) O((E+V) log V) O(E log E + (E+V)log V) Kruskal’s algorithm 1) sort the edges by weight 2) add edges in order if they do not create cycle

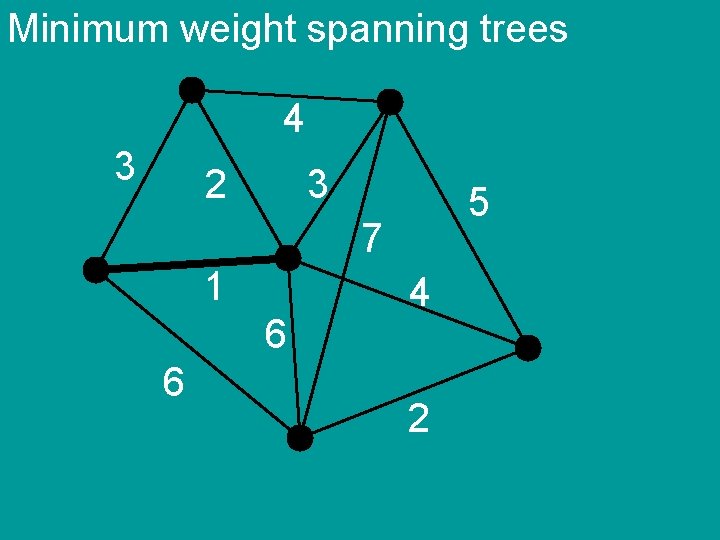
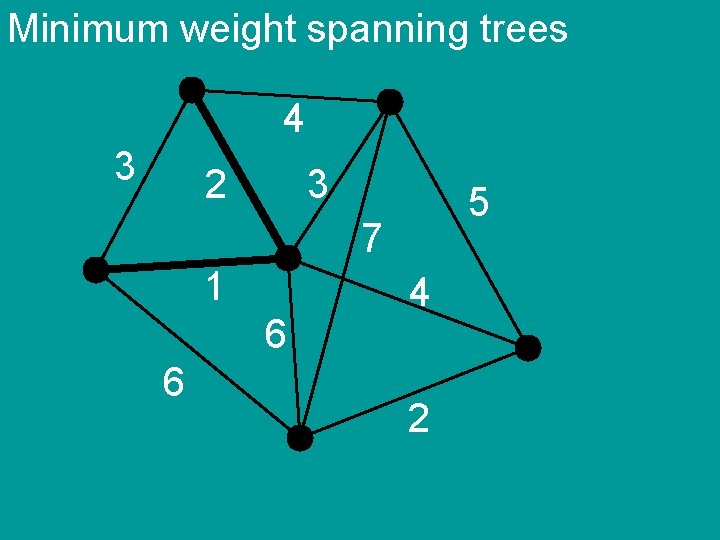
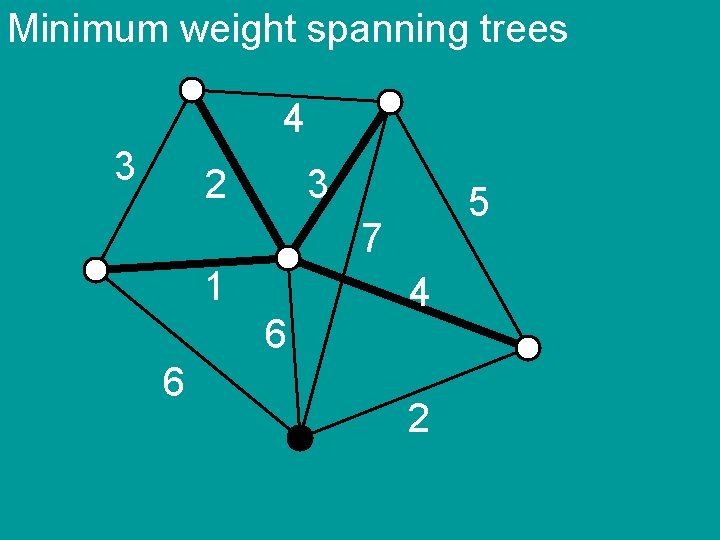
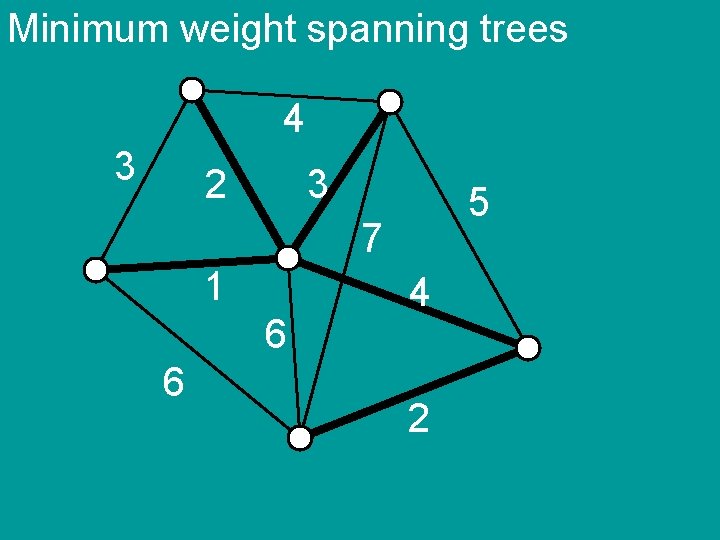
Minimum weight spanning trees 4 3 2 3 5 7 1 6 6 4 2

Minimum weight spanning trees 4 3 2 3 5 7 1 6 6 4 2

Minimum weight spanning trees 4 3 2 3 5 7 1 6 6 4 2

Minimum weight spanning trees 4 3 2 3 5 7 1 6 6 4 2

Minimum weight spanning trees 4 3 2 3 5 7 1 6 6 4 2

Minimum weight spanning trees 4 3 2 3 5 7 1 6 6 4 2

Minimum weight spanning trees Prim’s algorithm 1) S {1} 2) add the cheapest edge {u, v} such that u S and v SC S S {v} (until S=V)

Minimum weight spanning trees 1) S {1} 2) add the cheapest edge {u, v} such that u S and v SC S S {v} (until S=V) P = MST output by Prim T = optimal MST Is P = T ? assume all the edgeweights different

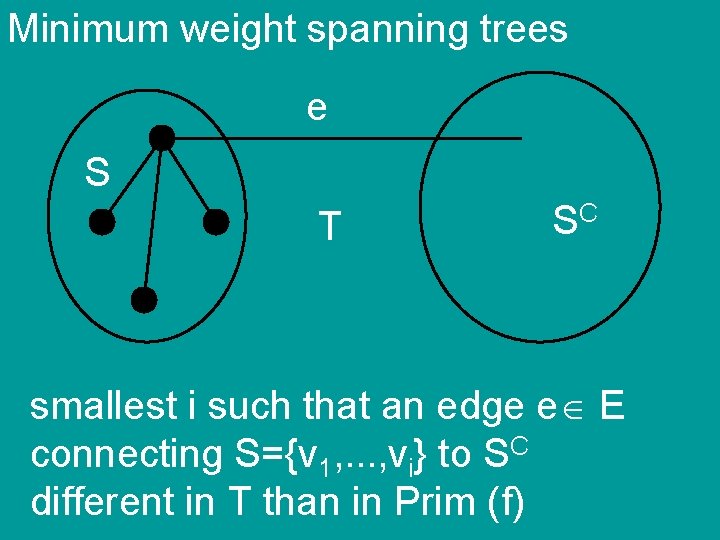
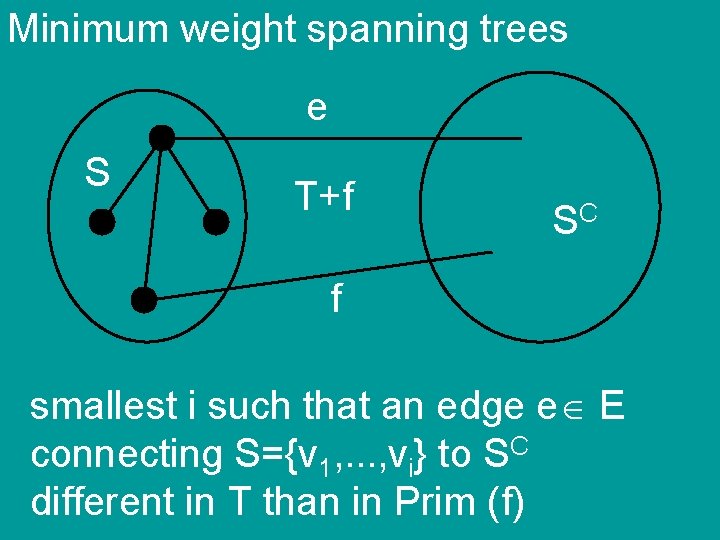
Minimum weight spanning trees P = MST output by Prim T = optimal MST P=T assuming all the edgeweights different v 1, v 2, . . . , vn order added to S by Prim smallest i such that an edge e E connecting S={v 1, . . . , vi} to SC different in T than in Prim (f)

Minimum weight spanning trees e S T SC smallest i such that an edge e E connecting S={v 1, . . . , vi} to SC different in T than in Prim (f)

Minimum weight spanning trees e S T+f SC f smallest i such that an edge e E connecting S={v 1, . . . , vi} to SC different in T than in Prim (f)
![Minimum weight spanning trees for i 1 to n do Ci C00 S while Minimum weight spanning trees for i 1 to n do C[i] C[0]=0 S={} while](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-53.jpg)
Minimum weight spanning trees for i 1 to n do C[i] C[0]=0 S={} while S V do j smallest such that j SC and C[j] is minimal S S { j } for u neighbors of j do if w[{j, u}] < C[u] then C[u] w[{j, u}]; P[u] j
![Minimum weight spanning trees for i 1 to n do Ci C00 On S Minimum weight spanning trees for i 1 to n do C[i] C[0]=0 O(n) S={}](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-54.jpg)
Minimum weight spanning trees for i 1 to n do C[i] C[0]=0 O(n) S={} while S V do j smallest such that j SC and C[j] is minimal S S { j } for u neighbors of j do if w[{j, u}] < C[u] then C[u] w[{j, u}]; P[u] j
![Minimum weight spanning trees for i 1 to n do Ci C00 On S Minimum weight spanning trees for i 1 to n do C[i] C[0]=0 O(n) S={}](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-55.jpg)
Minimum weight spanning trees for i 1 to n do C[i] C[0]=0 O(n) S={} while S V do j smallest such that j SC and C[j] is minimal S S { j } for u neighbors of j do if w[{j, u}] < C[u] then C[u] w[{j, u}]; P[u] j O(V 2 + E) = O(V 2)
![Minimum weight spanning trees for i 1 to n do Ci C00 Olog n Minimum weight spanning trees for i 1 to n do C[i] C[0]=0 O(log n)](https://slidetodoc.com/presentation_image_h2/ebc1d14dd8f187d1032d00d2a3abb439/image-56.jpg)
Minimum weight spanning trees for i 1 to n do C[i] C[0]=0 O(log n) S={} while S V do j smallest such that j SC and C[j] is minimal S S { j } for u neighbors of j do if w[{j, u}] < C[u] then C[u] w[{j, u}]; P[u] j O((E+V)log V) using heap

Minimum weight spanning trees Kruskal Prim O( (E+V) log V)

Minimum weight spanning trees Kruskal O( (E+V) log V) if edges already sorted then O(E log*V) Prim O( (E+V) log V) can be made O(E + V log V) using Fibonacci heaps