Higher Maths Revision Notes goodbye Functions and Graphs

Higher Maths Revision Notes goodbye Functions and Graphs Get Started

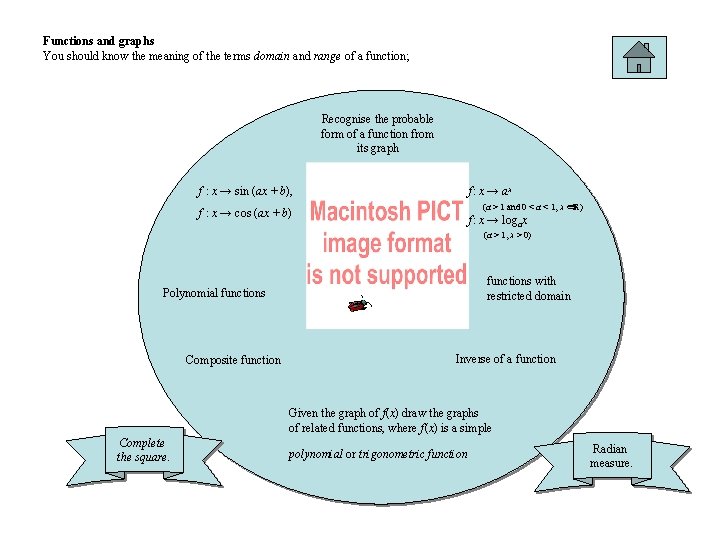
Functions and graphs You should know the meaning of the terms domain and range of a function; Recognise the probable form of a function from its graph f : x → sin (ax + b), f: x → ax (a > 1 and 0 < a < 1, x ∈R) f : x → cos (ax + b) f: x → logax (a > 1, x > 0) functions with restricted domain Polynomial functions Composite function Inverse of a function Given the graph of f(x) draw the graphs of related functions, where f(x) is a simple Complete the square. polynomial or trigonometric function Radian measure.

Shift to left wavelength In both graphs • a = 360 ÷ wavelength. • b = shift to the left a. … the number of waves in 360˚. Example: Find the equation of the blue curve if it is of the form y = sin(ax + b). Imagine the red curve, the corresponding function of the form y = sin(ax). The wavelength is 120˚ The shift to the left is 60 – 40 = 20˚ a = 360 ÷ 120 = 3 b = 20 3 = 60 The blue curve has equation y = sin(3 x + 60)˚ Test Yourself?

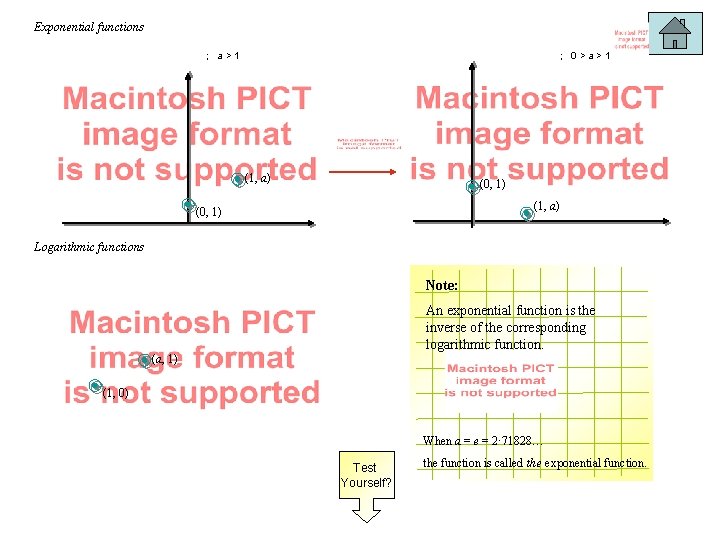
Exponential functions ; a>1 ; 0>a>1 (1, a) (0, 1) Logarithmic functions Note: An exponential function is the inverse of the corresponding logarithmic function. (a, 1) (1, 0) When a = e = 2· 71828… Test Yourself? the function is called the exponential function.

Polynomial functions In general a polynomial of order n will have at most n real roots and at most (n – 1) stationary points. e. g. a cubic can have, at most, 3 real roots and 2 s. p. s If a cubic has 3 real roots a, b and c then its equation will be of the form y = k(x – a)(x – b)(x – c) where k is a constant. If a, b and c are known then k can be calculated if one point the curve passes through is also known. When the brackets are expanded the cubic will have the form y = px 3 + qx 2 + rx + s, where p, q, r, and s are constants and p ≠ 0 Constant: y = a Similar statements can be made of the other polynomials. linear: y = ax + b quadratic: y = ax 2 + bx + c Test Yourself? cubic: y = ax 3 + bx 2 + cx + d quartic: y = ax 4 + bx 3 + cx 2 + dx + e

Restricted domain Reciprocal functions Square root function Others y = tan(x) then x ≠ 90, 270 or 90 + 180 n where n is an integer. The denominator can never equal zero. The term within the radical sign must always be ≥ 0 So a value of x which makes this happen is not in the domain. So any value of x which makes this negative is not in the domain. For example y = log(x) then x > 0 y = sin– 1(x) y = cos– 1(x) then – 1 ≥ x > 1 Test Yourself?

inverse If f(g(x)) = x and g(f(x)) = x for all x in the domain then we say that f is the inverse of g and vice versa. The inverse of f is denoted by f– 1. Examples [over suitable domains] • f(x) = x 2 … f– 1(x)= √x • f(x) = sin(x) … f– 1(x) = sin– 1(x) • f(x) = 2 x + 3 … f– 1(x) = (x – 3)/2 • f(x) = loga(x) … f– 1(x) = ax • f(x) = ex … f– 1(x) = ln(x) For the Higher exam you need not know how to find the formula for the inverse of any function. composites

Composite functions Example Suppose we have two functions: f(x) = 3 x + 4 and g(x) = 2 x 2 + 1. We can use these definitions to create new functions: 1 f(f(x)) 2 = f(3 x + 4) g(g(x)) 3 = g(2 x 2 + 1) 2(2 x 2 + 1)2 = 3(3 x + 4) + 4 = +1 = 9 x + 16 = 8 x 4 + 8 x 2 + 3 f(g(x)) 4 g(f(x)) = f(2 x 2 + 1) = g(3 x + 4) = 3(2 x 2 + 1) + 4 = 2(3 x + 4)2 + 4 = 6 x 2 + 7 = 18 x 2 + 48 x + 36 Things to note: • A composition can be made from more than two functions • Considering examples 1 and 2 leads to recurrence relations e. g. f(f(x))))) • In general f(g(x)) ≠ g(f(x)) … the order in which you do things are important. • If either f or g have restrictions on their domain, this will affect the domain of the composite function. • If f(g(x)) = x for all x in the domain then we say that f is the inverse of g … it can be denoted by g– 1 Test Yourself?

Related functions y = f(x + a) y = f(x) + a [x-translation of –a] [y-translation of a] y = af(x) y = –f(x) [stretch in y-direction] [reflection in x-axis] y = f(ax) y = f(–x) [squash in x-direction] [reflection in y-axis] y = f– 1(x) y = f ´(x) [The inverse] [The derivative] Test Yourself?

Completing the square We can use this identity to simplify quadratic expressions. Example 1 Express x 2 + 6 x + 1 in the form (x + a)2 Example 2 (a) Express 3 x 2 + 12 x + 1 in the form a(x + b)2 – c (b) Find the smallest value the expression can take. +b Given x 2 + 6 x + 1 (a) Given 3 x 2 + 12 x + 1, Take 3 out as a common factor leaving the coefficient of x 2 as 1 So 3(x 2 + 4 x) +1 … focus on the red text. By inspection a = 6 ÷ 2 = 3 So x 2 + 6 x + 1 = (x + 3)2 – 32 + 1 By inspection a = 4 ÷ 2 = 2 So we get 3(x 2 + 4 x) +1 = 3[(x + 2)2 – 22] + 1 = 3(x + 2)2 – 12 + 1 = 3(x +2)2 – 11 = (x + 3)2 – 8 Note: a = 3 and b = – 8 • Test Yourself? The smallest a perfect square can be is zero. So the smallest the expression can be is 0 – 11 = 11. Ths happens when x = – 2.

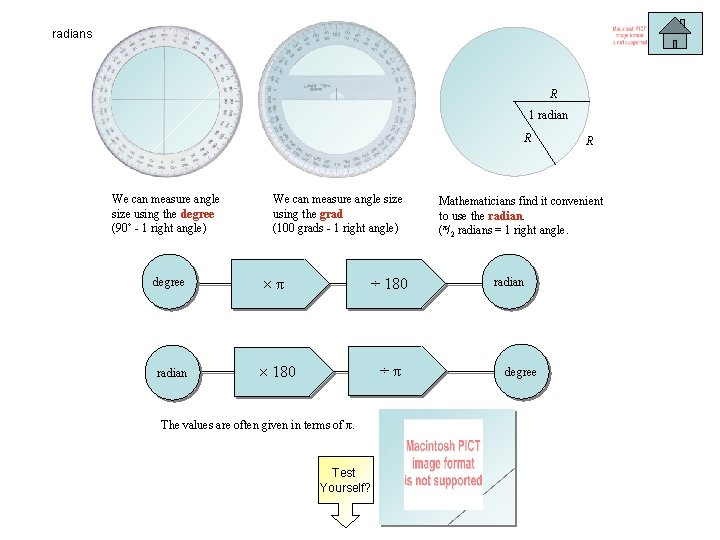
radians R 1 radian R We can measure angle size using the degree (90˚ - 1 right angle) degree radian We can measure angle size using the grad (100 grads - 1 right angle) π ÷ 180 ÷π The values are often given in terms of π. Test Yourself? R Mathematicians find it convenient to use the radian. (π/2 radians = 1 right angle. radian degree

y = f(x + a) [x-translation of –a] – 1

y = f(x) + a [y-translation of a] – 5

y = –f(x) [reflection in x-axis]

y = f(–x) [reflection in y-axis]

Stationary points of the function correspond to zeros of the derived function. Negatve gradients of the function correspond to Parts above the axis on the derived function. + Positive gradients of the function correspond to Parts below the axis on the derived function. – – + + + – + + Gradient of the function is shown in red y = f ´(x) [The derivative] +

When a function has an inverse then, if (x, y) lies on the graph of the function, (y, x) lies on the graph of the inverse function. …one is the reflection of the other in the line y = x. y = f– 1(x) [The inverse] Note that the example function does not have an inverse. The reflection in y = x has, for example, 3 values corresponding to x = 5.

y = f(ax) [squash in x-direction]

y = af(x) [stretch in y-direction]

Using suitable units, the distance of the tip of the rotor to the tail of a helicopter can be calculated using a formula of the form D = 3 sin(ax + b) + 10. The graph is shown below. What are the values of a and b reveal

Using suitable units, the distance of the tip of the rotor to the tail of a helicopter can be calculated using a formula of the form D = 3 sin(ax + b) + 10. The graph is shown below. What are the values of a and b Note: The 10 translates the sine wave 10 units up. The 3 stretches the wave by a factor of 3 in the y-direction. The wavelength, by inspection, is 120˚. a = 360 ÷ 120 = 3 One would expect the first peak of y = sin(3 x) to occur at 90 ÷ 3 = 30. It occurs at 15. Thus the shift to the left is 30 – 15 = 15. So b = shift a = 15 3 = 45. The equation is: D = 3 sin(3 x + 45) + 10

reveal The profile of the Eiffel tower can be modelled by the formula y = a ln(bx) where a and b are constants and y m is the height of a spot on the profile and x is its distance measured horizontally from the centre. When y = 0, x = 63. When y = 42, x = 40. Find the values of a and b.

When y = 0, x = 63 y = a ln(bx) 0 = a ln (63 b) ln(63 b) = 0 63 b = 1 b = 1/63 When y = 42, x = 40 y = a ln(bx) 42 = a ln (40 ÷ 63) 42 = a – 0· 454255 … (calculator) a = – 92 (to nearest whole number) Eiffel tower can be modelled by The profile of the Eiffel tower can be modelled by the formula y = a ln(bx) where a and b are constants and y m is the height of a spot on the profile and x is its distance measured horizontally from the centre. When y = 0, x = 63. When y = 42, x = 40. Find the values of a and b. y = – 92 ln(x/63)

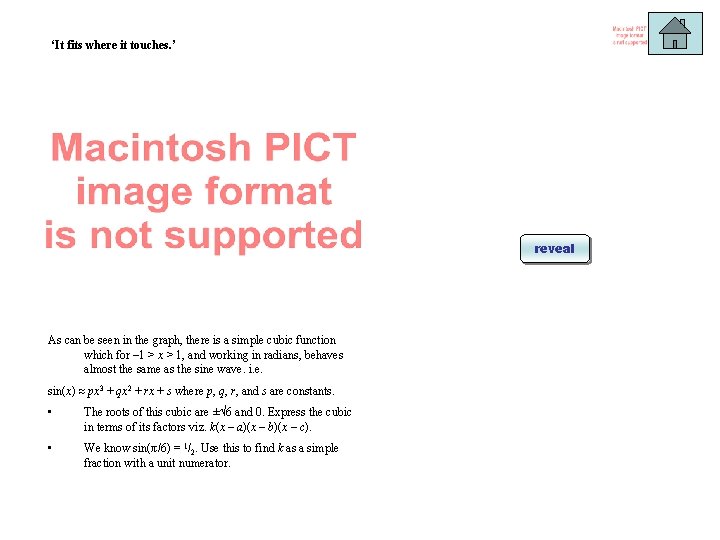
‘It fits where it touches. ’ reveal As can be seen in the graph, there is a simple cubic function which for – 1 > x > 1, and working in radians, behaves almost the same as the sine wave. i. e. sin(x) px 3 + qx 2 + rx + s where p, q, r, and s are constants. • The roots of this cubic are ± 6 and 0. Express the cubic in terms of its factors viz. k(x – a)(x – b)(x – c). • We know sin(π/6) = 1/2. Use this to find k as a simple fraction with a unit numerator.

‘It fits where it touches. ’ (a) (b) As can be seen in the graph, there is a simple cubic function which for – 1 > x > 1, and working in radians, behaves almost the same as the sine wave. i. e. sin(x) px 3 + qx 2 + rx + s where p, q, r, and s are constants. • The roots of this cubic are ± 6 and 0. Express the cubic in terms of its factors viz. k(x – a)(x – b)(x – c). • We know sin(π/6) = 1/2. Use this to find k as a simple fraction with a unit numerator.

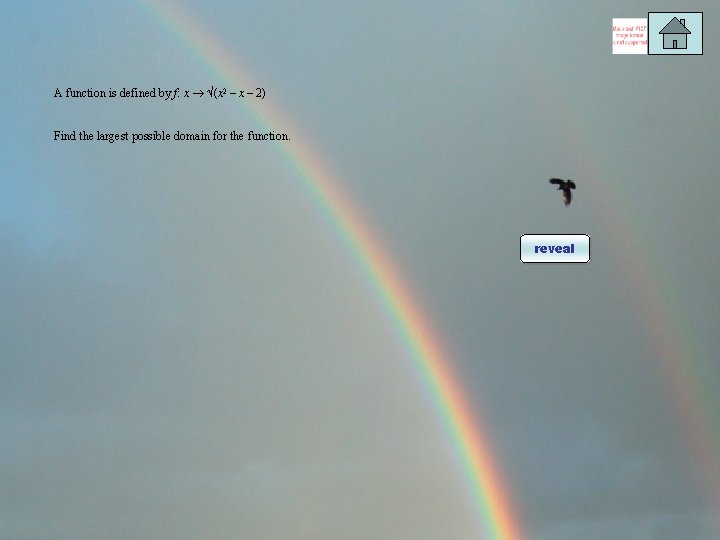
A function is defined by f: x (x 2 – x – 2) Find the largest possible domain for the function. reveal

A function is defined by f: x (x 2 – x – 2) Find the largest possible domain for the function. The function within the radical sign must be greater than or equal to zero. The sketch of this quadratic tells us that x ≥ 2 or x ≤ – 1. The sketch on the left shows the function in question.

f(x) = 2 x – 1 and g(x) = x 2 + 2. (a) Find an expression for f(g(x). (b) In general f(g(x)) ≠g(f(x)). However, in this case there are two values of x for which f(g(x)) = g(f(x)). (a) Find these values. reveal

f(x) = 2 x – 1 and g(x) = x 2 + 2. (a) Find an expression for f(g(x). (b) In general f(g(x)) ≠g(f(x)), (a) however, in this case there are two values of x for which f(g(x)) = g(f(x)). (a) f(g(x) = f(x 2 + 2) = 2(x 2 + 2) – 1 = 2 x 2 + 3 Find these values. (a) g(f(x)) = g(2 x – 1) = (2 x – 1)2 + 2 (a) (b) = 4 x 2 – 4 x + 3 g(f(x)) = f(g(x) (c) 4 x 2 – 4 x + 3 = 2 x 2 + 3 (d) 2 x 2 – 4 x = 0 (e) x(x – 2) = 0 (f) x = 0 or � x=2

(0· 75, 1) reveal The sketch shows part of the function y = f(x) (a) Draw a sketch of (i) y = f(–x) (b) Make a sketch of y = f´(x) (ii) y = f(1 – x)

(a (i)) (0· 75, 1) (a (ii)) The sketch shows part of the function y = f(x) (a) Draw a sketch of (i) y = f(–x) (b) Make a sketch of y = f´(x) (ii) y = f(1 – x) (b)

Where completing the square is useful Q 1 Find the maximum value of the function defined by: reveal Q 2 Prove that y = 3 x 3 + 3 x 2 + 5 x + 1 is an increasing function.

Where completing the square is useful Q 1 Find the maximum value of the function defined by: Q 1 In Higher maths you don’t know how to differentiate this function. Complete the square on the denominator: x 2 + 4 x + 9 = (x + 2)2 – 22 + 9 = (x + 2)2 + 5. The smallest this expression can be is when the bracket takes the value zero … When x = – 2, the expression is worth 5. This is when the function will be at its biggest. f(– 2) = 1/5 Q 2 To prove the function is always increasing , you have to prove that the derivative is always positive. Prove that y = 3 x 3 + 3 x 2 + 5 x + 1 is an increasing function. Complete the square: The minimum value of the derivative is 4. Thus its always positive and thus Always increasing.

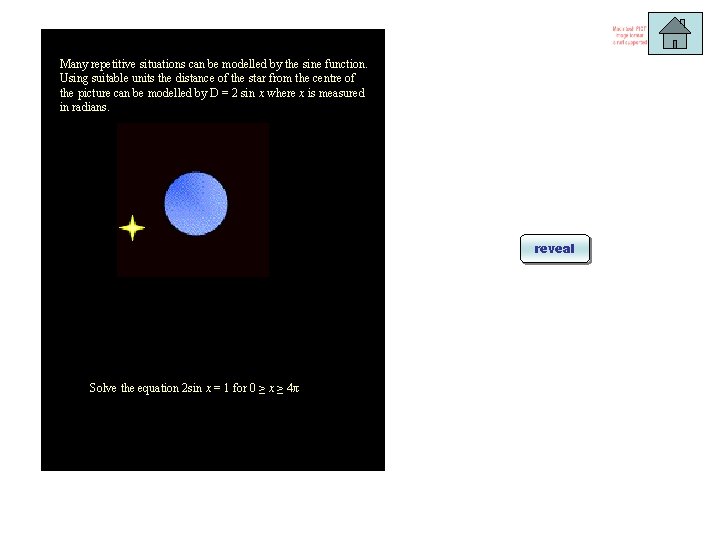
Many repetitive situations can be modelled by the sine function. Using suitable units the distance of the star from the centre of the picture can be modelled by D = 2 sin x where x is measured in radians. reveal Solve the equation 2 sin x = 1 for 0 ≥ x ≥ 4π

Many repetitive situations can be modelled by the sine function. Using suitable units the distance of the star from the centre of the picture can be modelled by D = 2 sin x where x is measured in radians. or any number of complete revolutions more (or less) than these two solutions … Solve the equation 2 sin x = 1 for 0 ≥ x ≥ 4π All other ‘answers’ are outside the desired range.