Higher Maths Circles 2 4 1 Higher Maths

Higher Maths Circles 2 4 1

Higher Maths Circles 2 4 2 B ( x 2 , y 2 ) Distance Between Two Points d √( x 2 – x 1)²+ ( y 2 – = Example The Distance Formula Calculate the distance between (-2, 9) and (4, -3). d = y 2 – y 1)² √ 6² + 12² = √ 180 = 6√ 5 A ( x 1 , y 1 ) x 2 – x 1 Where required, write answers as a surd in its simplest form.

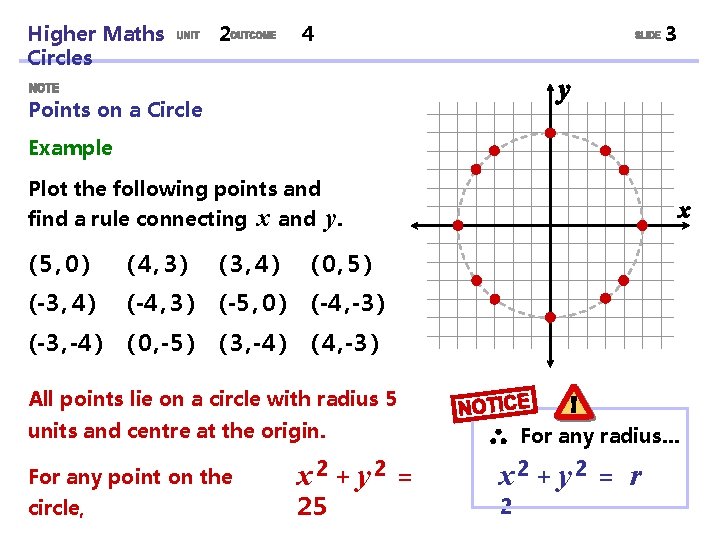
Higher Maths Circles 2 4 3 Points on a Circle Example Plot the following points and find a rule connecting x and y. (5, 0) (4, 3) (3, 4) (0, 5) (-3 , 4 ) (-4 , 3 ) (-5 , 0 ) (-4 , -3 ) (-3 , -4 ) ( 0 , -5 ) ( 3 , -4 ) ( 4 , -3 ) All points lie on a circle with radius 5 units and centre at the origin. For any point on the circle, x² + y² = 25 For any radius. . . x² + y² = r ²

Higher Maths Circles 2 4 4 The Equation of a Circle with centre at the Origin For any circle with radius r The and centre the origin, ‘Origin’ x² + y² = r ² is the point (0, 0) Substitute point into equation: Example Show that the point (-3 , 7 ) lies on the circle with equation x² + y² = origin 16 x ² + y ² = (-3)² + (7 )² = 9 + 7 = 16 The point lies on the circle.

Higher Maths Circles 2 4 5 The Equation of a Circle with centre (a, r b. Not ) all circles are centered at the origin. For any circle with radius and centre at the point. . . (a, b) r (a, b) ( x – a )² + ( y – b )² = ² ( x – a )² + ( y – b )² = Example Write the equation of the circle with centre ( 3 , -5 ) and radius r 2 3. ² ( x – 3 ) ² + ( y – (-5) ) ² ² ( x – 3 )² + ( y + 5 )² 12 r = 2( 3 ) =

Higher Maths Circles 2 4 6 The General Equation of a Circle Try expanding the equation of a circle with centre ( x + g )2 + ( y + f )2 = 2 2 2 r 2 2 ( x + 2 g x + g ) + ( y + 2 fy + f ) = r 2 2 2 ( -g , - f ). this is just a number. . . c = g 2 + f 2 – r 2 2 x + y + 2 g x + 2 f y + g + f – r = 0 r 2 x 2 + y 2 + 2 g x + 2 f y + c = 0 r = g 2 + f 2 – c = General Equation of a Circle with center ( -g , - f ) and radiusr = g 2 + f 2 – c

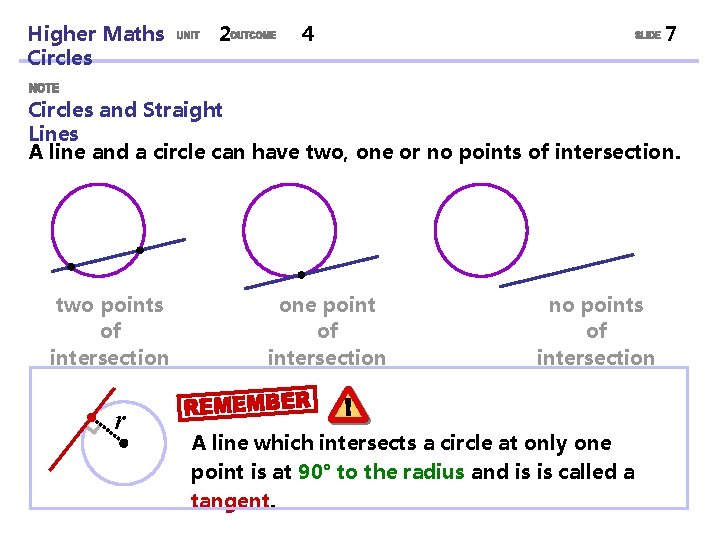
Higher Maths Circles 2 4 7 Circles and Straight Lines A line and a circle can have two, one or no points of intersection. two points of intersection r one point of intersection no points of intersection A line which intersects a circle at only one point is at 90° to the radius and is is called a tangent.

Higher Maths Circles 2 4 8 Intersection of a Line and a Circle How to find the points of intersection between a line and a circle: • rearrange the equation of the line into the form • substitute y = mx + c • solve the quadratic for Example intersection of the circle x 2 + y 2 = 45 2 x – y = 0 and the line into the equation of the circle x and substitute into m x + c to find y y = 2 x x = 3 or -3 x 2 + (2 x)2 = 45 Find the y = mx + c x 2 + 4 x 2 = 45 5 x 2 = 45 x 2 = 9 y = 2 x Substitute into : y = 6 or -6 Points of intersection are (3, 6) and (-3, -6).

Higher Maths Circles 2 4 9 Intersection of a Line and a Circle (continued) Example 2 y+8 = 0 x 2 + y 2 + 4 x + 2 y – 20 Find where the line 2 x – intersects the circle = 0 x 2 + (2 x + 8)2 + 4 x + 2 (2 x + 8) – 20 x 2 + 4 x 2 + 32 x + 64 + 4 x + 16 – 20 5 x 2 + 40 x + 60 = 0 5( x 2 + 8 x + Factorise 12 ) = 0 and solve 5( x + 2)( x + 6) = 0 x = 0 = -2 or -6 Substituting into y = 2 x + 8 points of intersection as (-2, 4) and (-6, -4).

Higher Maths Circles 2 4 10 The Discriminant and Tangents The discriminant can be used to x = -b ± b 2 – (4 ac ) show that a line is a tangent: • substitute y = m x + c into the circle equation • rearrange to form a quadratic equation • evaluate the discriminant 2 – (4 Two points of )>0 b ac b 2 – (4 ac ) = 0 intersection The line is a tangent b 2 – (4 ac ) < 0 No points of intersection 2 a b 2 – (4 ac ) Discriminan t r

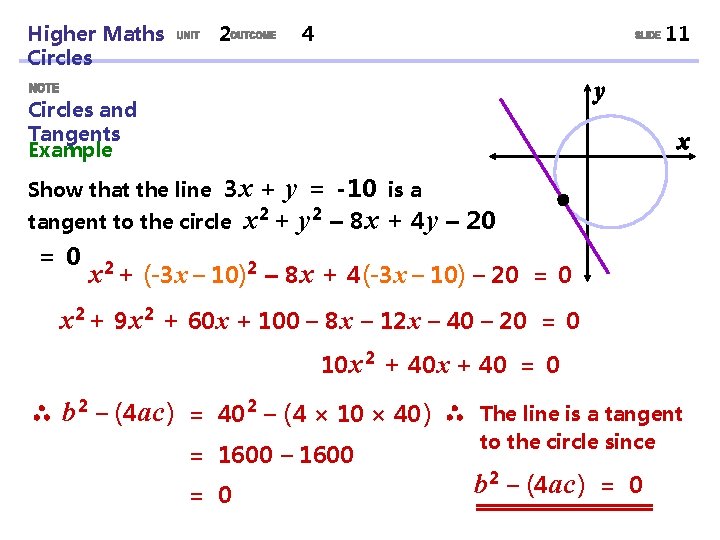
Higher Maths Circles 2 4 11 Circles and Tangents Example y = -10 is a x 2 + y 2 – 8 x + 4 y – 20 Show that the line 3 x + tangent to the circle = 0 x 2 + (-3 x – 10)2 – 8 x + 4 (-3 x – 10) – 20 x 2 + 9 x 2 + 60 x + 100 – 8 x – 12 x – 40 – 20 = 0 10 x 2 + 40 x + 40 = 0 b 2 – (4 ac ) = 40 2 – ( 4 × 10 × 40 ) = 1600 – 1600 = 0 The line is a tangent to the circle since b 2 – (4 ac ) = 0

Higher Maths Circles 2 4 Equation of Tangents To find the equation of a tangent to a circle: • Find the center of the circle and the point where the tangent intersects • Calculate the gradient of the 12 y – b = m( x – a) Straight Line Equation m radius = y 2 x 2 – – radius using the gradient formula • Write down the gradient of the tangent • Substitute the gradient of the tangent and the point of intersection into y – b = m( x – a) r m tangent = – 1 m radius y 1 x 1