Mr Bartons Maths Notes Graphs 1 Straight Line

Mr Barton’s Maths Notes Graphs 1. Straight Line Graphs www. mrbartonmaths. com

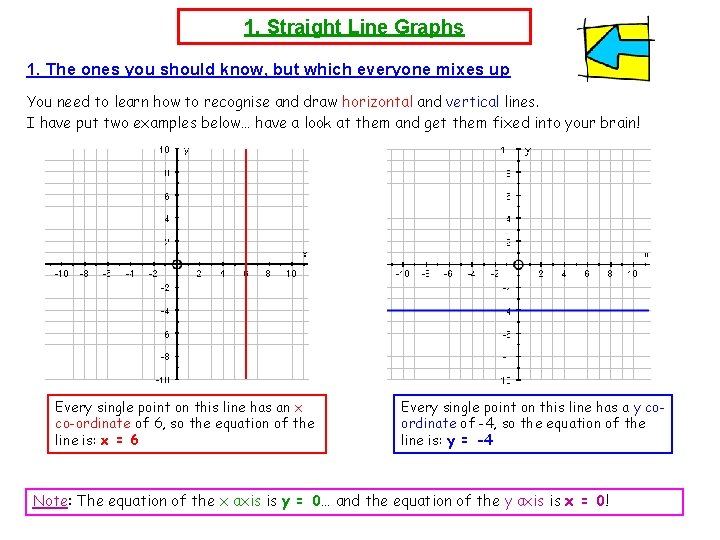
1. Straight Line Graphs 1. The ones you should know, but which everyone mixes up You need to learn how to recognise and draw horizontal and vertical lines. I have put two examples below… have a look at them and get them fixed into your brain! Every single point on this line has an x co-ordinate of 6, so the equation of the line is: x = 6 Every single point on this line has a y coordinate of -4, so the equation of the line is: y = -4 Note: The equation of the x axis is y = 0… and the equation of the y axis is x = 0!

2. What does the Equation of a Straight Line actually mean? The equation of a straight line is just a way of writing the relationship between the x coordinates and the y co-ordinates that lie on that line. Example: y = 2 x – 1 This says that the relationship between all the x co-ordinates and all the y co-ordinates is: “get your x co-ordinate, multiply it by 2, subtract 1, and you get your y co-ordinate” So…If a pair of co-ordinates has this relationship… such as (5, 9)… then it’s on the line If it doesn’t… such as (3, 2)… then it does not lie on the line What you end up with is just a straight line that goes through all the co-ordinates which share that relationship

3. Drawing Straight Line Graphs from their Equation As well as the horizontal and vertical lines, there are 2 other types of straight line graph equation, but they both follow the same general method: 1. Choose a sensible value of x… one that is small enough to fit on the paper, and easy enough for you to work out 2. Carefully substitute it into the equation to get your y value 3. Do this 4 times so you have four points 4. Join them up with a straight line Crucial: If one of your points does not lie on the straight line, then I’m afraid you have made a mistake… but at least you know which one is wrong so it should be easy to fix! Number 1 Classic Mistake People Make: Messing up their negative numbers… you must be very careful when substituting negative x’s One Final Top Tip Pick x = 0 as one of your points, as it is often nice and easy to work out the y value!

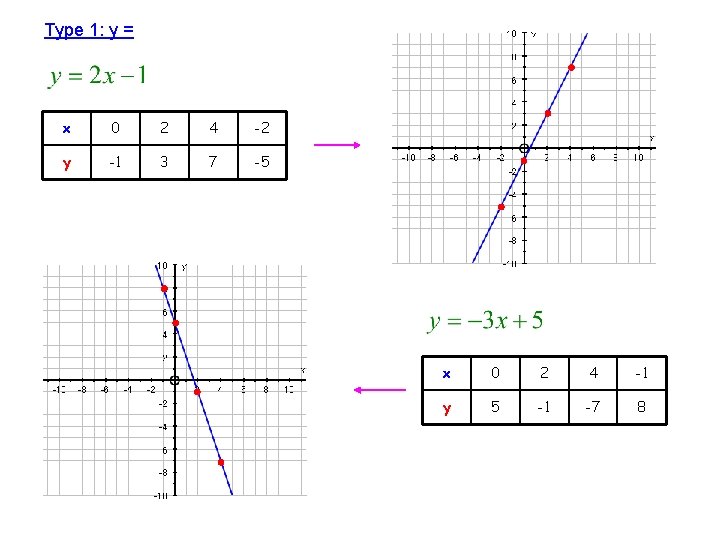
Type 1: y = x 0 2 4 -2 y -1 3 7 -5 x 0 2 4 -1 y 5 -1 -7 8

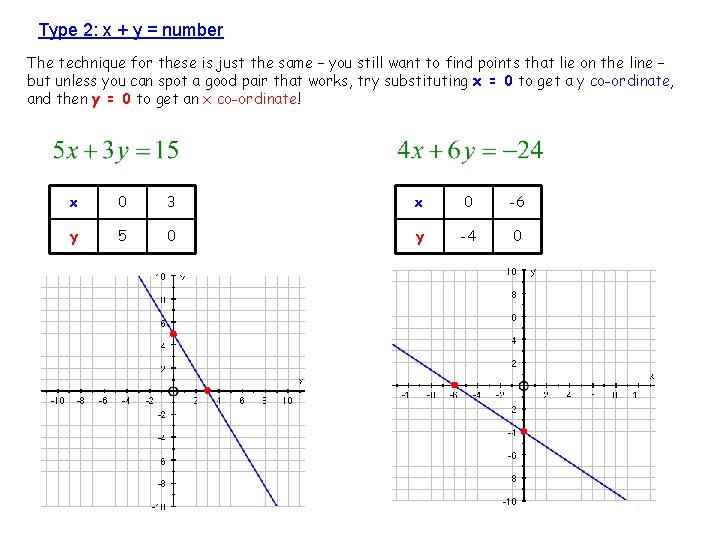
Type 2: x + y = number The technique for these is just the same – you still want to find points that lie on the line – but unless you can spot a good pair that works, try substituting x = 0 to get a y co-ordinate, and then y = 0 to get an x co-ordinate! x 0 3 x 0 -6 y 5 0 y -4 0

4. What can we learn from the Equation of a Line: y = mx + c The more Type 1 lines you draw, the more you should start noticing the link between the equation of the line, and what the line actually looks like These are the Big Facts that you need to know! m +c • This number tells you the gradient/steepness of the • This number tells you where the line crosses the y axis • The bigger the number, the steeper the line • Its posh name is the y intercept • If the number is positive, the line slopes upwards • If it is negative, the line slopes downwards • Parallel lines have the same gradient Classic Mistake: If the equation is NOT in the form: y = mx + c, you must first re -arrange it before you start saying what the gradient and intercept are!

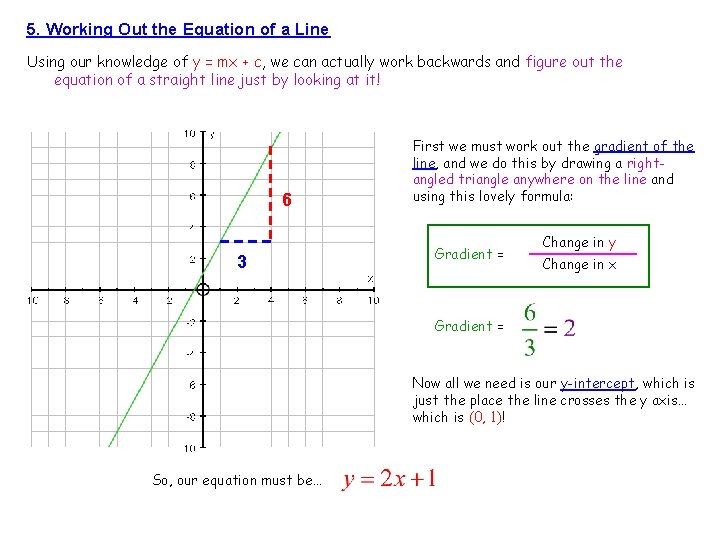
5. Working Out the Equation of a Line Using our knowledge of y = mx + c, we can actually work backwards and figure out the equation of a straight line just by looking at it! 6 3 First we must work out the gradient of the line, and we do this by drawing a rightangled triangle anywhere on the line and using this lovely formula: Gradient = Change in y Change in x Gradient = Now all we need is our y-intercept, which is just the place the line crosses the y axis… which is (0, 1)! So, our equation must be…

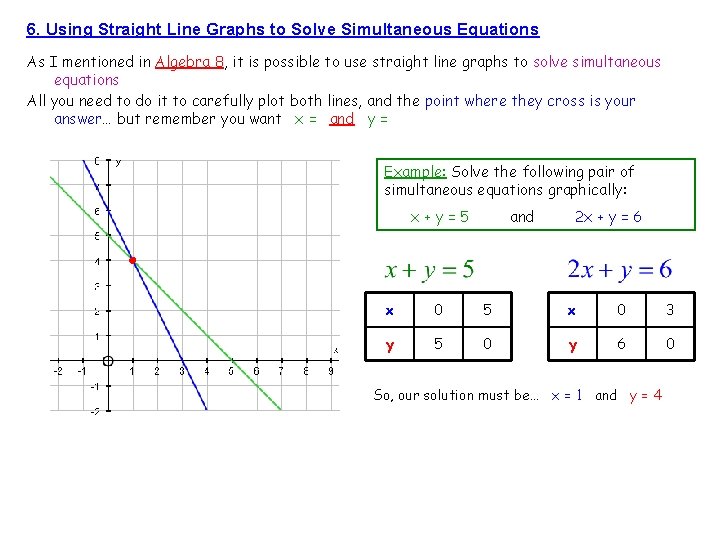
6. Using Straight Line Graphs to Solve Simultaneous Equations As I mentioned in Algebra 8, it is possible to use straight line graphs to solve simultaneous equations All you need to do it to carefully plot both lines, and the point where they cross is your answer… but remember you want x = and y = Example: Solve the following pair of simultaneous equations graphically: x+y=5 and 2 x + y = 6 x 0 5 x 0 3 y 5 0 y 6 0 So, our solution must be… x = 1 and y = 4

Good luck with your revision!