Greatest Common Divisor Jordi Cortadella Department of Computer

Greatest Common Divisor Jordi Cortadella Department of Computer Science

Simplifying fractions • greatest common divisor Introduction to Programming © Dept. CS, UPC 2

The largest square tile 4 4 h=24 w = 60 What is the largest square tile that can exactly cover a w h rectangle? 90 tiles of side-length 4 Introduction to Programming © Dept. CS, UPC 3

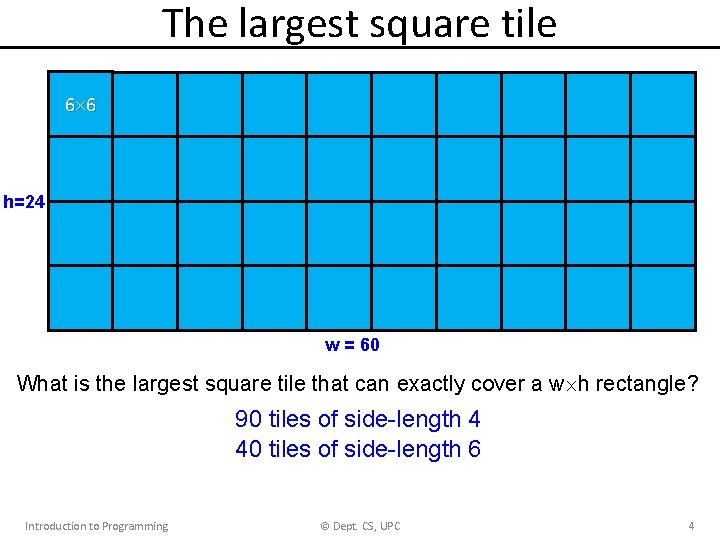
The largest square tile 6 6 h=24 w = 60 What is the largest square tile that can exactly cover a w h rectangle? 90 tiles of side-length 4 40 tiles of side-length 6 Introduction to Programming © Dept. CS, UPC 4

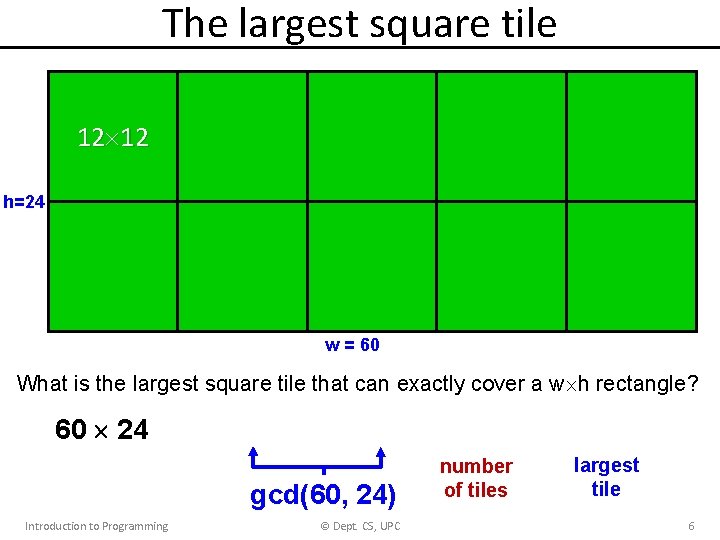
The largest square tile 12 12 h=24 w = 60 What is the largest square tile that can exactly cover a w h rectangle? 90 tiles of side-length 4 40 tiles of side-length 6 10 tiles of side-length 12 Introduction to Programming © Dept. CS, UPC 5

The largest square tile 12 12 h=24 w = 60 What is the largest square tile that can exactly cover a w h rectangle? 60 24 = (5 12) (2 12) = (5 2) (12 12) gcd(60, 24) Introduction to Programming © Dept. CS, UPC number of tiles largest tile 6

Euclid (300 B. C. ) A fragment of Euclid’s Elements http: //www. math. ubc. ca/~cass/Euclid/papyrus/tha. jpg Introduction to Programming © Dept. CS, UPC 7

Euclidean algorithm for gcd • Introduction to Programming © Dept. CS, UPC 8

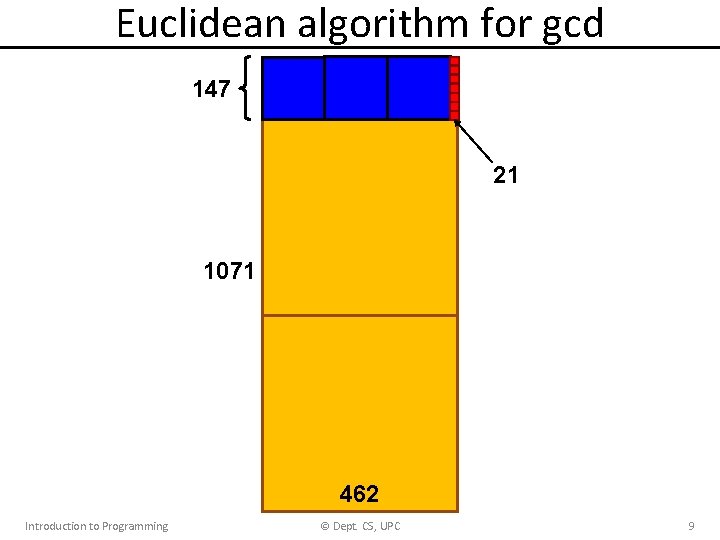
Euclidean algorithm for gcd 147 21 1071 462 Introduction to Programming © Dept. CS, UPC 9

Euclidean algorithm for gcd • Properties: gcd(a, a) = a; gcd(a, 0) = a If a b, then gcd(a, b) = gcd(a b, b) • Example: Introduction to Programming a 114 72 30 b 42 42 42 30 18 6 6 12 12 12 6 © Dept. CS, UPC gcd (114, 42) 10

Euclidean algorithm for gcd // Pre: a > 0, b > 0 // Returns the greatest common divisor of a and b int gcd(int a, int while (a != b) if (a > b) else b = b } return a; } Introduction to Programming b) { { a = a – b; – a; © Dept. CS, UPC 11

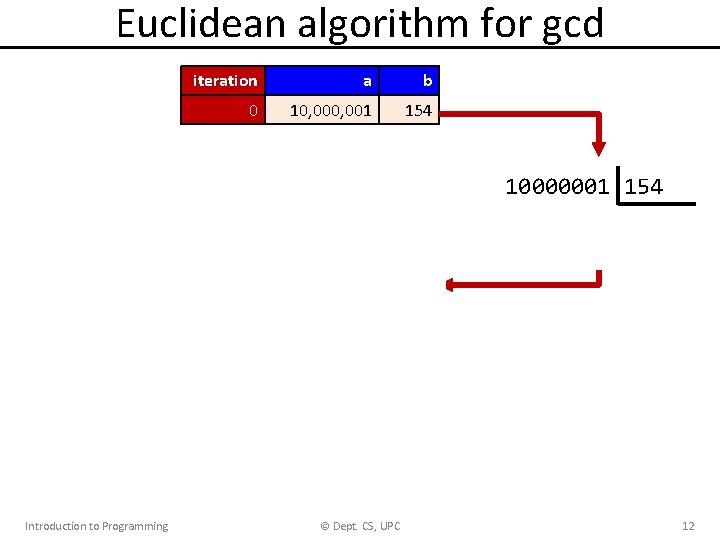
Euclidean algorithm for gcd Introduction to Programming iteration a b 0 10, 001 154 1 9, 999, 847 154 2 9, 999, 693 154 3 9, 999, 539 154 … … 154 64, 934 165 154 64, 935 11 154 64, 936 11 143 64, 937 11 132 64, 938 11 121 64, 939 11 110 … 11 … 64, 947 11 22 64, 948 11 11 © Dept. CS, UPC 10000001 154 11 64935 12

Faster Euclidean algorithm for gcd • Properties: gcd(a, 0) = a If b 0 then gcd(a, b) = gcd(a%b, b) • Example a 10, 001 11 11 Introduction to Programming © Dept. CS, UPC b 154 0 13

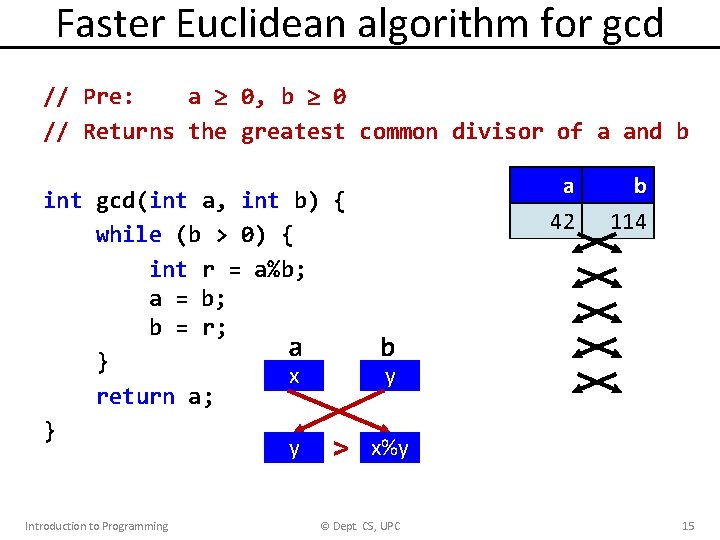
Faster Euclidean algorithm for gcd // Pre: a 0, b 0 // Returns the greatest common divisor of a and b int gcd(int a, int b) { while (a != 0 and b != 0) { if (a > b) a = a%b; else b = b%a; } return a + b; not } Termination: a == 0 or b == 0 Introduction to Programming © Dept. CS, UPC 14

Faster Euclidean algorithm for gcd // Pre: a 0, b 0 // Returns the greatest common divisor of a and b int gcd(int a, int b) { while (b > 0) { int r = a%b; a = b; b = r; a b } x y return a; } y > x%y Introduction to Programming © Dept. CS, UPC a 42 114 42 b 114 42 30 30 12 6 0 15

Comparing algorithms for gcd int gcd(int a, int b) { while (a > 0 and b > 0) { if (a > b) a = a%b; else b = b%a; } return a + b; } Every iteration: • 3 comparisons • 1 mod operation Introduction to Programming int gcd(int a, int b) { while (b > 0) { int r = a%b; a = b; b = r; } return a; } Every iteration: • 1 comparison • 1 mod operation © Dept. CS, UPC 16

Efficiency of the Euclidean algorithm How many iterations will Euclid’s algorithm need to calculate gcd(a, b) in the worst case (assume a > b)? – Subtraction version: a iterations (consider gcd(1000000, 1)) – Modulo version: 5 d(b) iterations, where d(b) is the number of digits of b (Gabriel Lamé, 1844) Introduction to Programming © Dept. CS, UPC 17

Binary Euclidean algorithm Computers can perform 2 and /2 operations efficiently (217)10 = (11011001)2 (217 2)10 = (434)10 = (110110010)2 (217/2)10 = (108)10 = (1101100)2 (217%2)10 = 1 (least significant bit) Introduction to Programming © Dept. CS, UPC 18

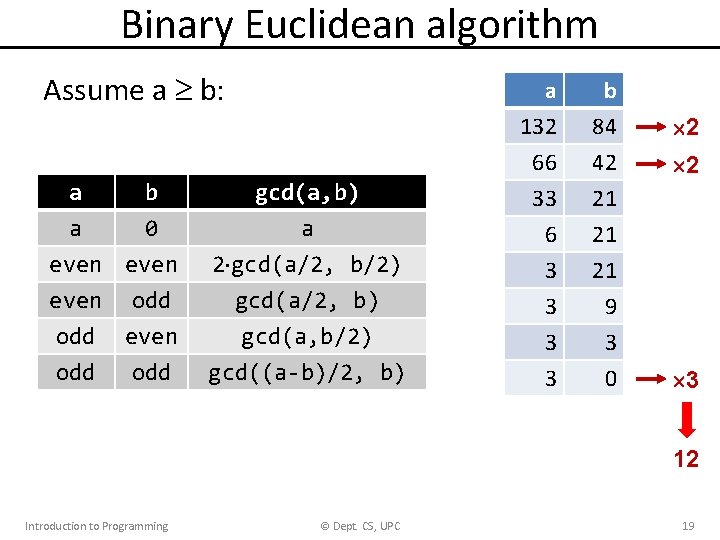
Binary Euclidean algorithm Assume a b: a a b 0 gcd(a, b) a even 2 gcd(a/2, b/2) even odd odd gcd(a/2, b) gcd(a, b/2) gcd((a-b)/2, b) a 132 66 33 b 84 42 21 6 3 3 21 21 9 3 0 2 2 3 12 Introduction to Programming © Dept. CS, UPC 19

Binary Euclidean algorithm // Pre: a 0, b 0 // Returns the greatest common divisor of a and b int gcd(int a, int b) { int r = 1; // Accumulates common powers of two while (a != 0 and b != 0) { if (a%2 == 0 and b%2 == 0) { a = a/2; b = b/2; r = r 2; } else if (a%2 == 0) a = a/2; else if (b%2 == 0) b = b/2; else if (a > b) a = (a - b)/2; else b = (b – a)/2; } return (a + b) r; } Introduction to Programming © Dept. CS, UPC 20

Binary Euclidean algorithm // Pre: a 0, b 0 // Returns the greatest common divisor of a and b int gcd(int a, int b) { if (a == 0 or b == 0) return a + b; int r while a b r } = 1; // Accumulates common powers of two (a%2 == 0 and b%2 == 0) { = a/2; = b/2; = r 2; while (a != b) { if (a%2 == 0) a = a/2; else if (b%2 == 0) b = b/2; else if (a > b) a = (a - b)/2; else b = (b – a)/2; } return a r; } Introduction to Programming © Dept. CS, UPC 21

Summary • Euclid’s algorithm is very simple. • It is widely used in some applications related to cryptography (e. g. , electronic commerce). • Euclid’s algorithm efficiently computes the gcd of very large numbers. • Question: how would you compute the least common multiple of two numbers efficiently? Introduction to Programming © Dept. CS, UPC 22