Approximate computations Jordi Cortadella Department of Computer Science

Approximate computations Jordi Cortadella Department of Computer Science

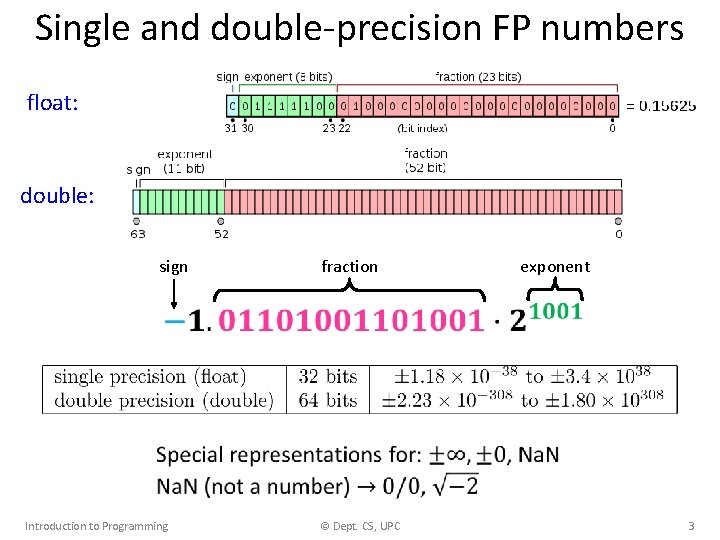
Representation of real numbers Decimal notation 2 5 . 3 7 Binary notation 5 Scientific notation (decimal): 1 1 0 0 1 1 Scientific notation (floating point): Every binary number can be represented in decimal, but not vice versa! Introduction to Programming © Dept. CS, UPC 2

Single and double-precision FP numbers float: double: sign fraction exponent Introduction to Programming © Dept. CS, UPC 3

Beware when operating with real numbers • Example (C++): double x, y; cin >> x >> y; // 1. 1 3. 1 cout. precision(20); cout << x + y << endl; // 4. 200000001776 • Example (Python): >>> a = 1/3 >>> b = 1/2 >>> a+b 0. 833333333 >>> a+b-a-b -5. 551115123125783 e-17 Introduction to Programming © Dept. CS, UPC 4

Comparing floating-point numbers • Comparisons: a = b + c if a – b == c: … # may be false • Allow certain tolerance for equality comparisons: if expr 1 == expr 2: … # Wrong! if abs(expr 1 – expr 2) < 1 e-7: … # 1 e-7 == 0. 0000001 Introduction to Programming © Dept. CS, UPC # Ok. 5

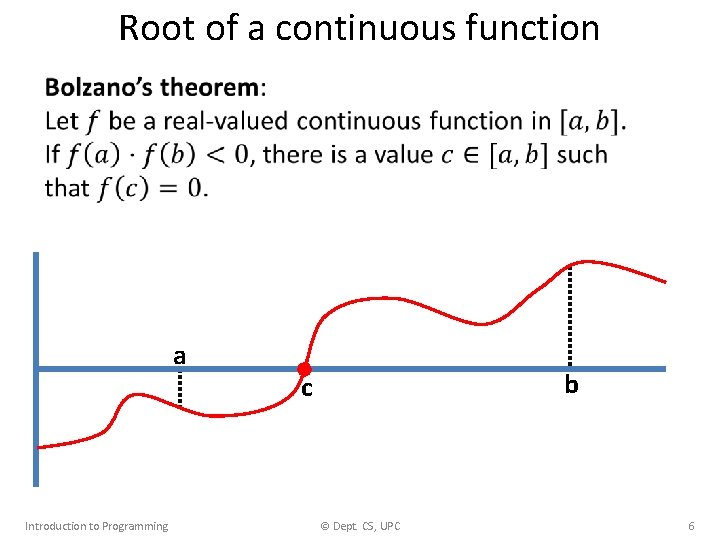
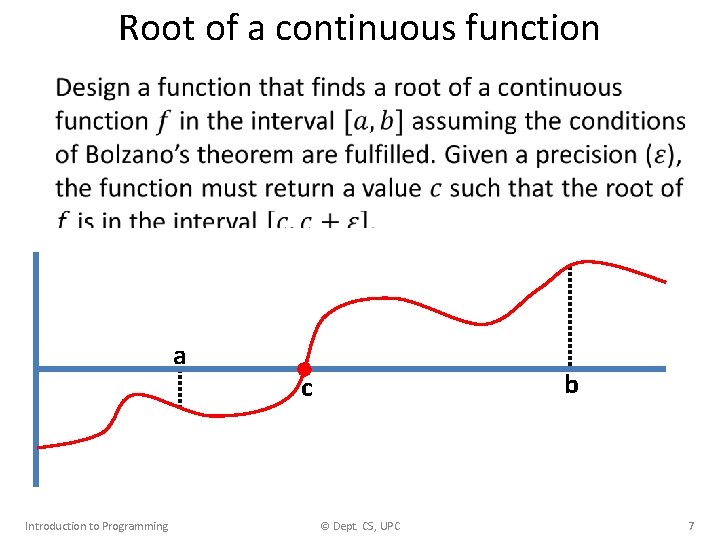
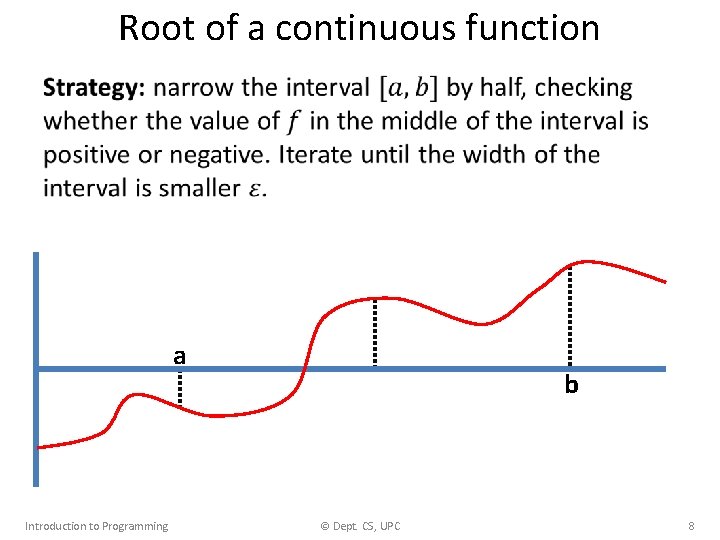
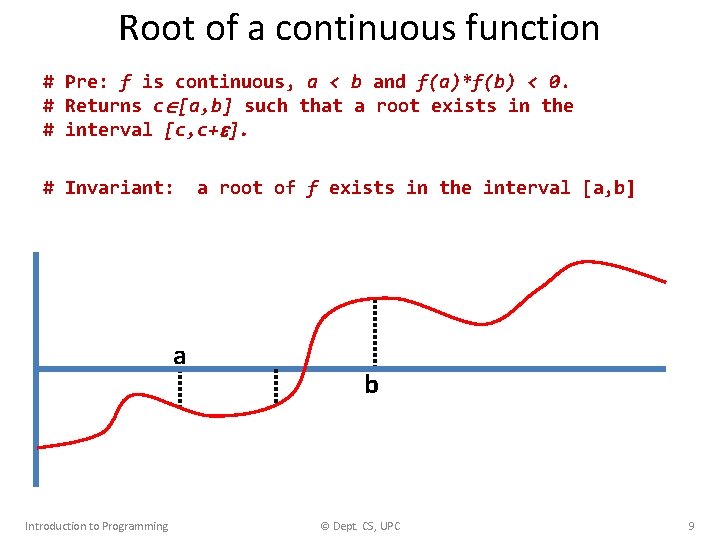
Root of a continuous function • a Introduction to Programming b c © Dept. CS, UPC 6

Root of a continuous function • a Introduction to Programming b c © Dept. CS, UPC 7

Root of a continuous function • a Introduction to Programming b © Dept. CS, UPC 8

Root of a continuous function # Pre: f is continuous, a < b and f(a)*f(b) < 0. # Returns c [a, b] such that a root exists in the # interval [c, c+ ]. # Invariant: a Introduction to Programming a root of f exists in the interval [a, b] b © Dept. CS, UPC 9

Root of a continuous function a Introduction to Programming © Dept. CS, UPC c b 10

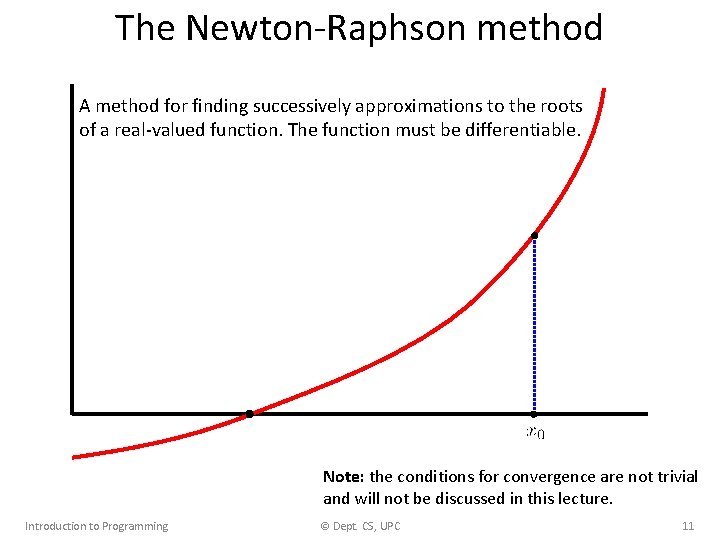
The Newton-Raphson method A method for finding successively approximations to the roots of a real-valued function. The function must be differentiable. Note: the conditions for convergence are not trivial and will not be discussed in this lecture. Introduction to Programming © Dept. CS, UPC 11

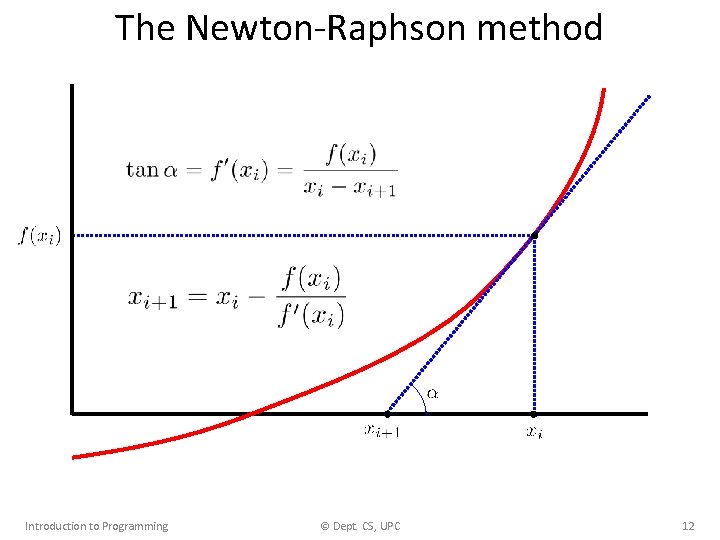
The Newton-Raphson method Introduction to Programming © Dept. CS, UPC 12

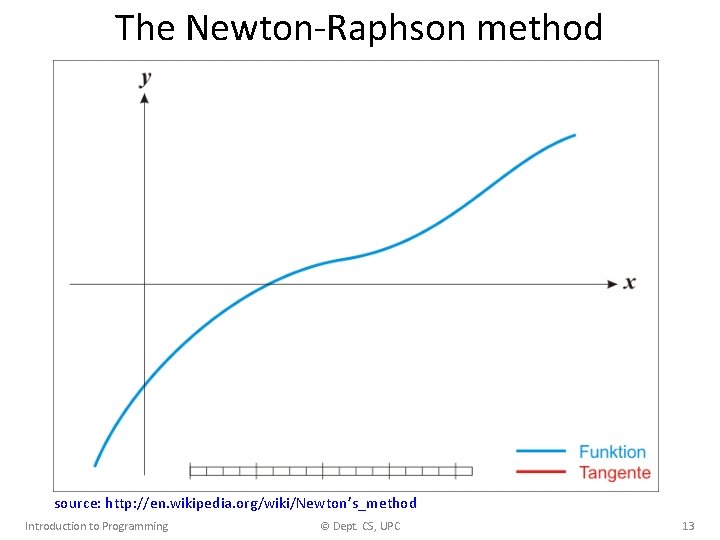
The Newton-Raphson method source: http: //en. wikipedia. org/wiki/Newton’s_method Introduction to Programming © Dept. CS, UPC 13

Square root (using Newton-Raphson) • Calculate • Find the zero of the following function: where • Recurrence: Introduction to Programming © Dept. CS, UPC 14

Square root (using Newton-Raphson) def square_root(a, epsilon): """Pre: a >= 0. Returns x such that |x 2 -a| < epsilon. """ x = 1 # Makes an initial guess # Iterates using the Newton-Raphson recurrence while abs(x x – a) >= epsilon: x = 0. 5 (x + a/x) return x Introduction to Programming © Dept. CS, UPC 15

Square root (using Newton-Raphson) Example: square_root(1024) x 1. 0000000000 512. 50000000000 257. 249024390332634 130. 61480157022683101786 69. 227324054488946103447 42. 009585631008270922848 33. 192487416854376647279 32. 021420905000240964000 32. 000007164815897908738 32. 000000802913291 Introduction to Programming © Dept. CS, UPC 16

Approximating definite integrals • There are various methods to approximate a definite integral: • The trapezoidal method approximates the area with a trapezoid: Introduction to Programming © Dept. CS, UPC 17

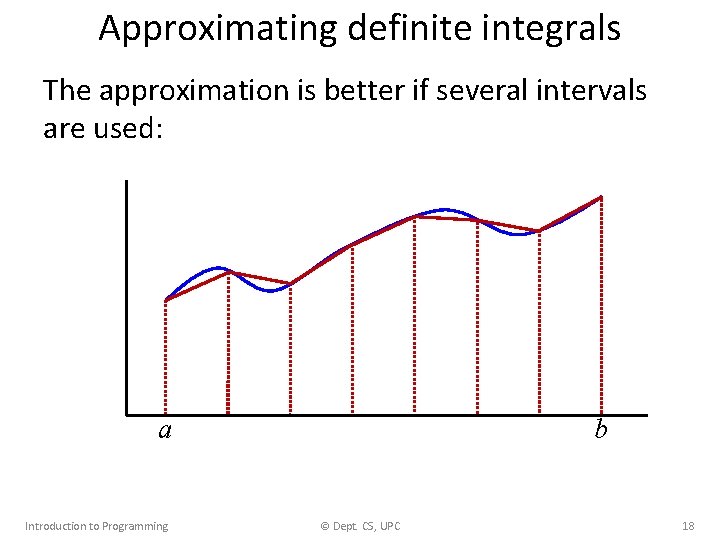
Approximating definite integrals The approximation is better if several intervals are used: a Introduction to Programming b © Dept. CS, UPC 18

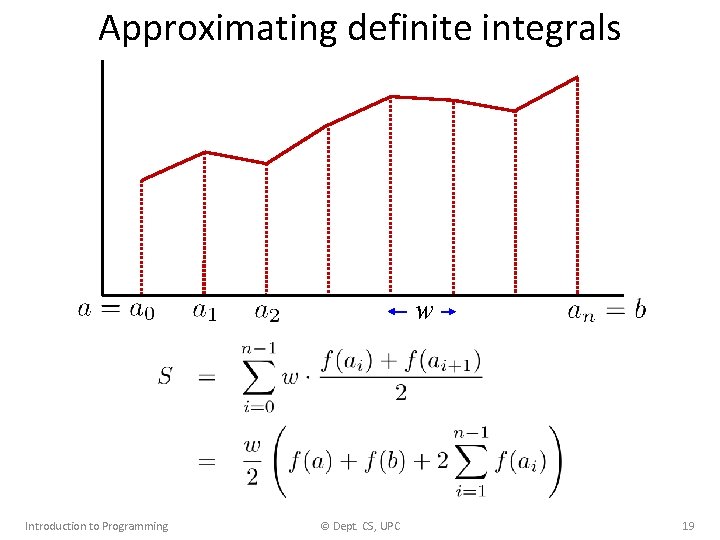
Approximating definite integrals w Introduction to Programming © Dept. CS, UPC 19

Approximating definite integrals def integral(f, a, b, n): """Pre: b >= a, n > 0. Returns an approximation of the definite integral of f between a and b using n intervals. """ w = (b – a)/n # width of the interval s = 0 for i in range(1, n): s += f(a + i w) return (f(a) + f(b) + 2 s) w/2 Introduction to Programming © Dept. CS, UPC 20

Summary • Approximate computations is a resort when no exact solutions can be found numerically. • Intervals of tolerance are often used to define the level of accuracy of the computation. • Recommendation: allow some interval of tolerance when doing comparisons with floating point numbers. Introduction to Programming © Dept. CS, UPC 21